函数式编程本质

• 支持 高阶函数 (higher-order functions)

• 追求 函数调用没有副作用 (no side-effect)

Related Concepts

• First-class & Higher-order Functions

• Pure Functions

• Currying

• Function Composition

• Hindley-Milner

• Pattern Matching

• Lambda Calculus

• Lazy Evaluation

• Functor、Applicative Functor & Monad

First-class Functions

First-class functions are values, and can be used in every way that typical expressions can.

assigning to variables

const foo = funxtion() { return 'Hey, js-functional' }

foo() // => 'Hey, js-functional'

storing in data structures

const obj = {
  foo: function() { return 'Hey, js-functional' },
}

obj.foo() // => 'Hey, js-functional'

returning by functions

const bar = function() {
  return function() { return 'Hey, js-functional' }
}

const foo = bar()
foo() // => 'Hey, js-functional'

passing as arguments to other functions

const baz = function(func) { return func() }

baz(function() { return 'Hey, js-functional' })
// => 'Hey, js-functional'

Higher-order functions

A higher-order function is a function that does at least one of the following:

• takes one or more functions as arguments.
• returns a function as its result.

function noisy(fun) {
  return function() { return fun.apply(null, arguments) }
}

noisy(Boolean)(0) // => false
noisy(Boolean)(1) // => true

Pure Functions

A function where the return value is only determined by its input values, without observable side effects. ​

• Given the same input, will always return the same output.
• Produces no side effects.
• Relies on no external state.

Math.random() // => 0.1599823728657992
Math.random() // => 0.10539394558259518

// `Math.random()` is not pure.


Math.sqrt(2) // => 1.4142135623730951

关于函数副作用(side-effect)

变更了更高作用域的的变量

let glob = 1
function foo(x) { return ++glob + x }
console.log(foo(1)) // => 3

关于函数副作用(side-effect)

“隐晦”地修改了引用参数

let glob = 1
const obj = {glob}
function foo(x) { return ++x.glob }
foo(obj)
console.log(glob) // => 2

Benefits of Pure Functions

• Cacheable & Memoization
• portable, easier to test & parallelize
• Referential Transparent
• can be lazy

memoize技术: 递归函数性能优化

/**
  f(0) = 0
  f(1) = 1
  f(n) = f(n-1) + f(n-2) (n > 1)
**/

function fibonacci(n) {
  if (n === 0 || n === 1) return n
  return fibonacci(n-1) + fibonacci(n-2)
}

console.log(fibonacci(7))
console.log(fibonacci(40))

以存储空间换执行效率

const fibonacci = (function() {
  const cache = {}

  return function fib(n) {
    if (n in cache) return cache[n]
    return (cache[n] = (n === 0 || n === 1) ? n : fib(n-1) + fib(n-2))
  }
})()

console.log(fibonacci(7))
console.log(fibonacci(40))

memoize函数的JS实现

function memoize(func) {
  const memo = {}
  const slice = Array.prototype.slice

  return function() {
    const args = slice.call(arguments)

    if (args in memo) return memo[args]
    return (memo[args] = func.apply(this, args))
  }
}

const memoizedFibonacci = memoize(fibonacci)

console.log(memoizedFibonacci(7))
console.log(memoizedFibonacci(40))

引用透明(Referential Transparent)

An expression is said to be referentially transparent if it can be replaced with its corresponding value without changing the program’s behavior.

# 中国的首都是个美丽的城市。


# 北京是个美丽的城市。

举例：函数推导

如何理解 Curry 化函数？

一個函數当且仅当只能容许拥有一个参数

假設, js 語法有這樣的限制：

    function max(a, b) {
      return a > b ? a : b;
    }

    max(10086, 10010);
    // => 10086

function max(a) {
  return function(b) {
    return a > b ? a : b;
  }
}

max(10086)(10010);
// => 10086

继续举例

function addFourNumbers(a, b, c, d) {
  return a + b + c + d;
}

addFourNumbers(1, 3, 5, 7);
// => 16

function curriedAddFourNumbers(a) {
  return function(b) {
    return function(c) {
      return function(d) {
        return a + b + c + d;
      }
    };
  }
}

curriedAddFourNumbers(2)(4)(6)(8);
// => 20

借助一些工具：ramdajs

const R = require('ramda')

const addFourNumbers = function(a, b, c, d) {
    return a + b + c + d
}

const curriedAddFourNumbers = R.curry(addFourNumbers)

curriedAddFourNumbers(1)(3)(5)(7)
//=> 16

// 或
const f = curriedAddFourNumbers(1)
const g = f(3)
const h = g(5)
h(7)
//=> 16

Why Curry Needs

Heron's Formula

Calculate the area of a triangle while only knowing the length of all three sides.

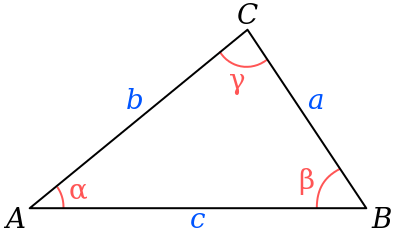
// 根据三条边的长度判断是否能够构成一个三角形
function isTriangle(a, b, c) {
  return (a>0 && b > 0 && c > 0 && a+b > c && a+c > b && b+c > a)
}


// 根据三角形三条边的边长计算其面积
function heronFormula(a, b, c) {
  if (!isTriangle(a, b, c)) throw new Error('Illegal triangle')

  const p = (a+b+c) / 2

  return Math.sqrt(p*(p-a)*(p-b)*(p-c))
}


// 计算已知一条边长为3，其它两条边未知的的三角形面积
function foo(x, y) {
  return heronFormula(3, x, y)
}

/**
 *
 * 如果已知边长为4，其它两条边未知的求其三角形面积
 * 是不是要再实现一遍与foo(x,y)结构完全类似的函数？
 *
 **/

const R = require('ramda')

// 对 heronFormula() 函数进行Curry化
const curriedHeronFormula = R.curry(heronFormula)


// 〔新函数〕计算其中一个边长为3的三角形面积
const foo = curriedHeronFormula(3)

// 〔新函数〕计算其中两条边长分别为3，4的三角形面积
const bar = foo(4)

// 〔结果〕计算边长分别为3，4，5的三角形面积
console.log(bar(5))
// => 6

通过Curry化，能够更加精简地实现函数复用

当然，Curry本质意义在于：将函数完全变成「接受一个参数；返回一个值」的固定形式，这样对于讨论和优化更加方便。

Partial Functions

Function Composition

const compose = (f, g) => x => f(g(x))

pointfree

const getAdminEmails = function(users) {
  const emails = [];
  for (var i = 0; i < users.length; i++) {
    if (users[i].role === 'admin') {
      emails.push(users[i].email)
    }
  }
  return emails
}

pointfree

const getAdminEmails = users =>
    users
      .filter(u => u.role === 'admin')
      .map(u => u.email)

pointfree

const getAdminEmails = users =>
    users
      .filter(u => u.role === 'admin')
      .map(u => u.email)

Hindley-Milner

大家都知道 1加1等于2；但是一个苹果加一个板凳等于什么呢？