Lecture 20
Reachability Analysis of
Hybrid Systems

Stanley Bak

Hybrid Automata

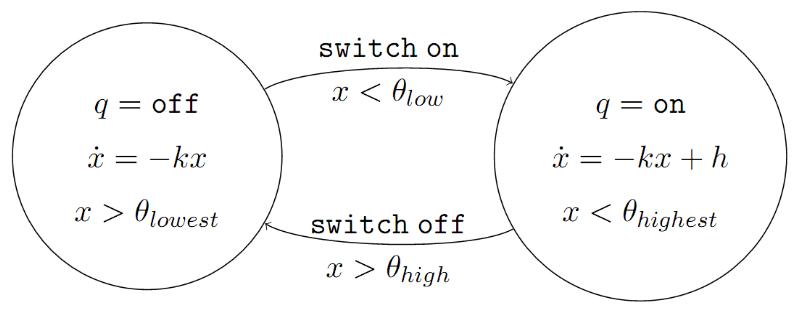
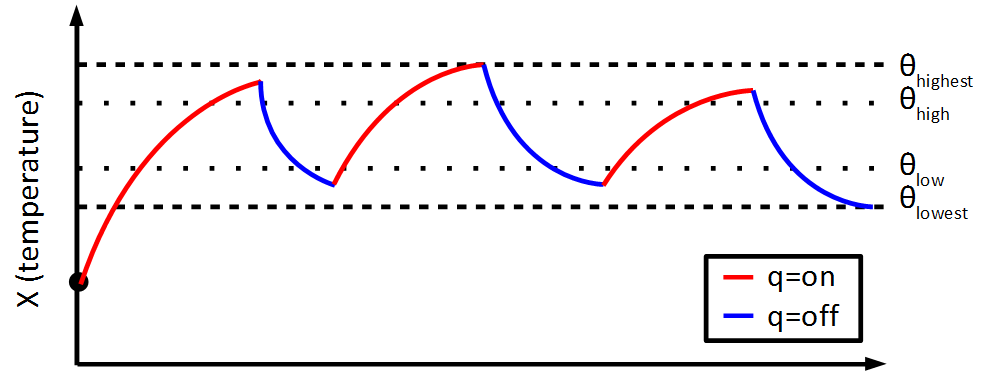
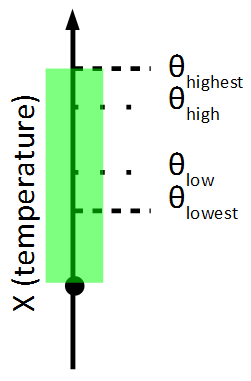
Set-Based Simulation

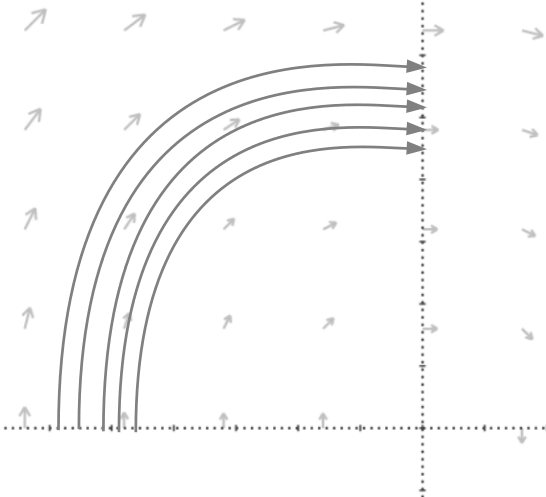
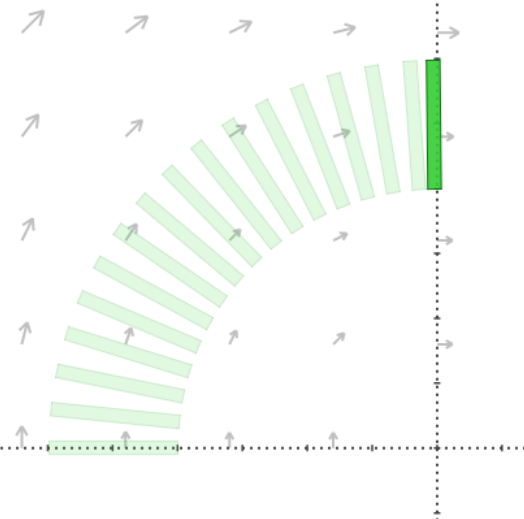
Sample and Simulate

Set-Based Simulation

Continuous / Discrete Post

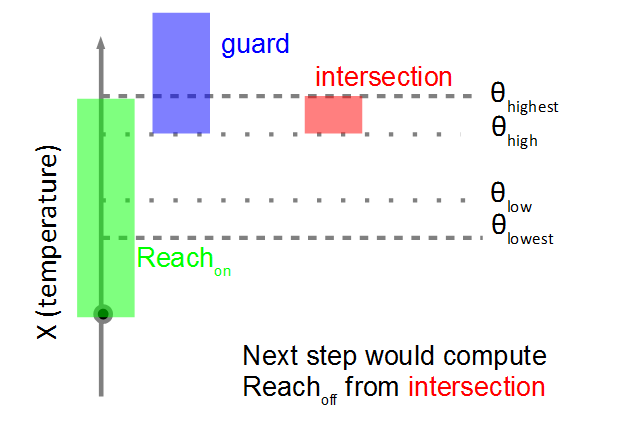
Aggregation in Discrete Post

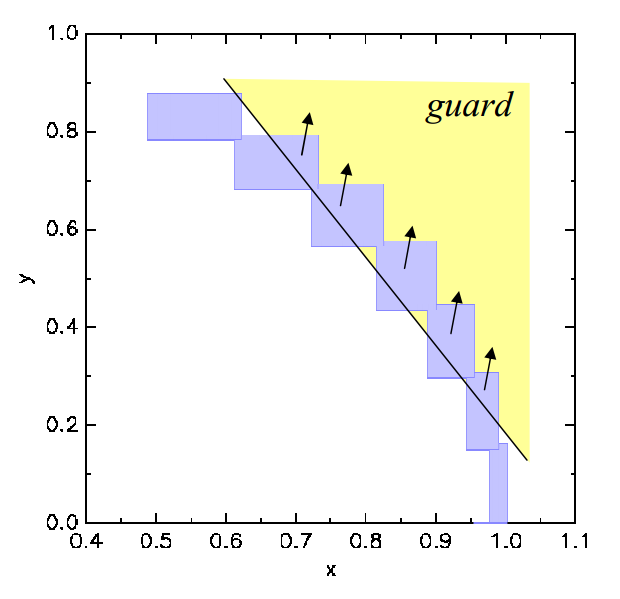
Image from: “Safety Analysis of Hybrid Systems  with SpaceEx,” Frehse et al., http://cmacs.cs.cmu.edu/seminars/slides/frehse.pdf

Set Operations are Needed

Flow-pipe construction (set-based simulation) for hybrid systems needs spatial data structures that efficiently support several operations:

• Time-elapse (linear transformation)
• Optimization (check for intersection)
• Bloating (Minkowski sum)
• Compute intersection
• Union
• Set Containment

Set Representation is a Choice

Ideally, all operations would be efficient in high dimensions

 

Some representations:

• Boxes (hyper-rectangles)
• Polytopes (Constraint Form)
• Polytopes (Vertex Form)
• Ellipsoids
• Zonotopes
• Support Functions
• Linear Star Sets
• Taylor Models (nonlinear)

Set Representation is a Choice

Ideally, all operations would be efficient in high dimensions

 

Some representations:

• Boxes (hyper-rectangles)
• Polytopes (Constraint Form)
• Polytopes (Vertex Form)
• Ellipsoids
• Zonotopes
• Support Functions
• Linear Star Sets
• Taylor Models (nonlinear)

Example: Spring-Mass System

Parameterized by the number of masses. Each mass adds two variables: (1) position and (2) velocity

$$x_n' = v$$

$$v_n' = \frac{-k(x_n – x_{n-1}) + k(x_{n+1} - x_n) }{m}$$

Example: Spring-Mass System

Parameterized by the number of masses. Each mass adds two variables: (1) position and (2) velocity

$$x_n' = v$$

$$v_n' = \frac{-k(x_n – x_{n-1}) + k(x_{n+1} - x_n) }{m}$$

Formal Specification

Specifications can be given in terms of linear constraints
on the state variables:

 

First mass doesn't touch the wall:

\(x_0 \geq \frac{\textnormal{width}}{2}\)

 

Masses \(n\) and \(n+1\) doesn't collide:

\(x_{n+1} - x_n \geq \textnormal{width}\)

 

Velocity of mass \(m\) is bounded:

\(v_m \leq 0.7 \)

Initial States

Is the specification violated from the start point:

$$[x_0, v_0, x_1, v_1, \ldots x_n, v_n] = [0, 0.8, 0, 0, \ldots 0]$$

 

For one mass (\(n=1\))? For two? for ten?

 

How can we check?

Spring-Mass
Simulation

Uncertainty

We had considered a single initial case, with

$$[x_0, v_0, x_1, v_1, \ldots x_n, v_n] = [0, 0.8, 0, 0, \ldots 0]$$

 

What if there was uncertainty in the initial states? Let's say every value was within a tolerance of \(\pm 0.2\).

 

How can we check if there are any start states that violate the safety specification?