演算法
v0.6.4 - by 晴☆
前情提要
你需要知道的事
你需要的基礎
- 基本的 C++ 語法
- 變數與運算
- 函數
- 條件與迴圈
- STL
- Struct & Class
- 清晰的邏輯
- 一些數學
什麼是演算法
其實就是演算的方法
演算的方法
思考如何更有效率的解決問題
就這樣
蛤？
看個例子大概就知道了
不過先講一下比較實際的東西
解題與競程
可以放學習歷程欸
APCS
就是「大學程式設計先修檢測」
- 可以放學習歷程
- 可以幫你上頂大
應該不用多說什麼了吧
免費的，大家都去考
然後去年的我沒有去考
Online Judge
就是「線上評測系統」
- 練習寫實作題目的地方
- 上傳你的程式碼，測試它是否能夠正常運作
舉個例子：
給高中生的 OJ
是資訊之芽的 OJ
全世界最大的 OJ
有按照難度排序的 OJ
怎麼使用？
寫題目
- 來看這個例子吧
- 首先會有題目敘述，告訴你這題要幹嘛
- 然後還有輸入輸出格式，你的程式碼要按照這個順序讀取輸入 & 輸出結果
- 看完題目就可以開始寫程式
- 寫完程式就可以上傳程式碼
- 然後就可以看它是不是正確的囉
不過大部分時候可能都不是正確的
#include <iostream>
int main() {
int a, b;
std::cin >> a >> b;
std::cout << a + b << "\n";
}放一下這題的解答好了
等等 我是特例嗎？
寫題目
#include <iostream>
int main() {
int a, b;
std::cin >> a >> b;
std::cout << a + b << "\n";
}放一下這題的解答好了
- 來看這個例子吧
- 首先會有題目敘述，告訴你這題要幹嘛
- 然後還有輸入輸出格式，你的程式碼要按照這個順序讀取輸入 & 輸出結果
- 看完題目就可以開始寫程式
- 寫完程式就可以上傳程式碼
- 然後就可以看它是不是正確的囉
不過大部分時候可能都不是正確的
結果
| 簡稱 | 全名 | 白話的意思 |
|---|---|---|
| AC | Accept | 通過啦～ |
| NA | Not Accept | 沒通過，只拿到部分的分數 |
| WA | Wrong Answer | 錯了，沒分數可以拿 QQ |
| TLE | Time Limit Exceeded | 太慢，超過時間限制 |
| MLE | Memory Limit Exceeded | 使用太多資源，超過記憶體限制 |
| RE | Runtime Error | 執行到一半出現錯誤 |
| CE | Compile Error | 編譯錯誤 |
需要注意的事
-
自己至少執行過一次
-
測資範圍
-
要不要開 long long
-
可不可以用 unsigned
-
- 極端測資
-
是不是有 0 或 -1 之類的
-
-
複雜度
不是啦 這個還沒講
複雜度
好複雜，我不懂
你要做多少事情
很多事情
看圖形
右邊有一些函數的圖形：
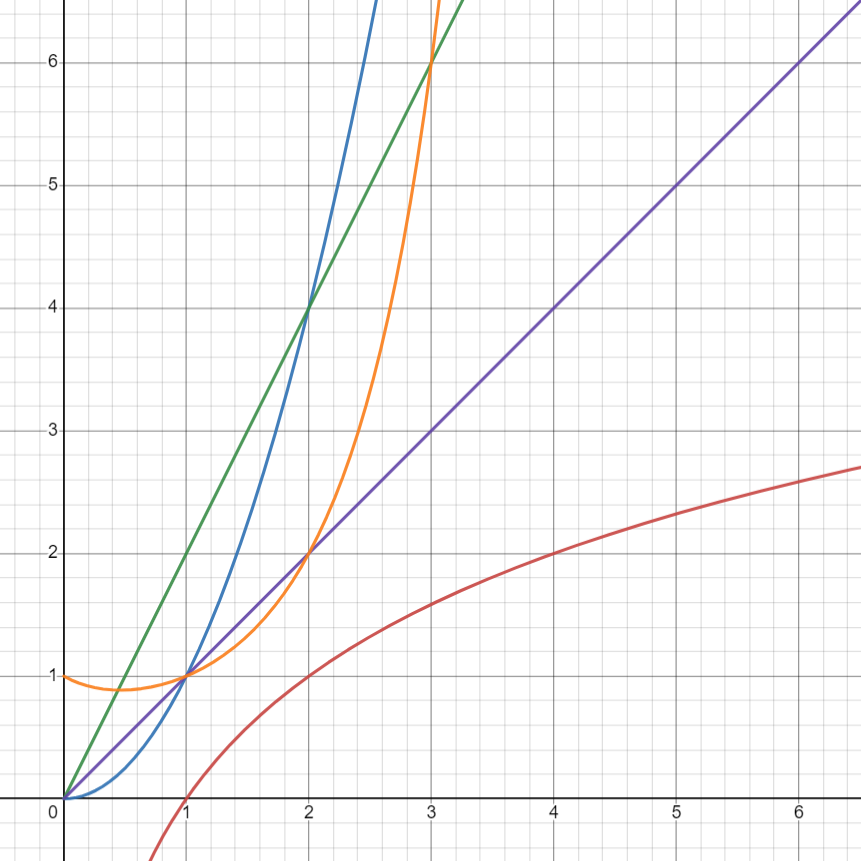
\(n\)
\(f(n)\)
- 紫色：\(x\)
- 綠色：\(2x\)
- 藍色：\(x^2\)
- 橘色：\(x!\)
- 紅色：\(log_2(x)\)
感覺很亂，什麼都看不出來？
縮小一點來看！
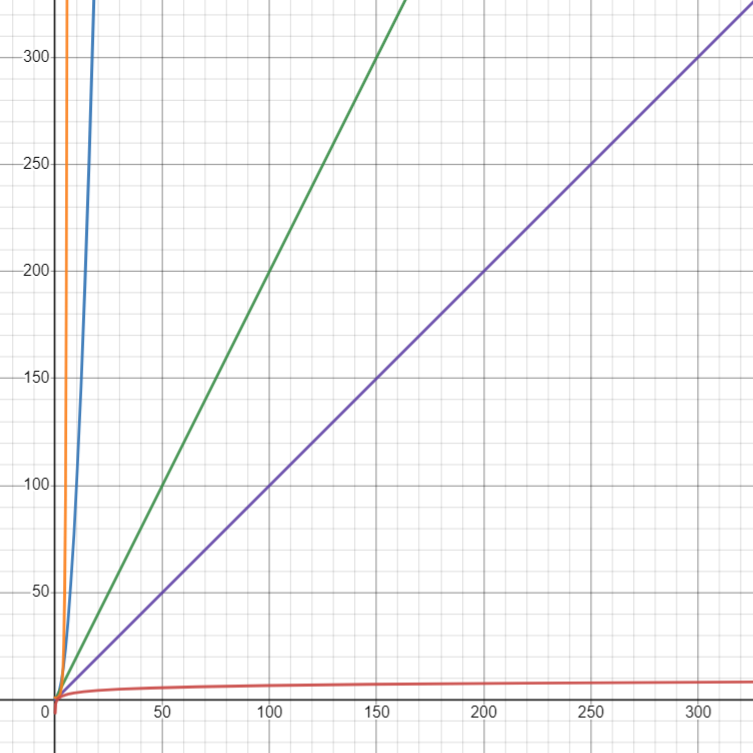
看圖形
右邊有一些函數的圖形：
\(n\)
\(f(n)\)
- 紫色：\(x\)
- 綠色：\(2x\)
- 藍色：\(x^2\)
- 橘色：\(x!\)
- 紅色：\(log_2(x)\)
感覺很亂，什麼都看不出來？
縮小一點來看！
\(x! > x^2 > 2x > x > log_2(x)\)
大致看得出速度關係了！
不過要注意一件事
從圖形不能看出真正的關係
比方說：
\(2^{16} x\ 和\ 2^{32} x\\看起來差不多但實際上差很多\)！
看數字
演算法的目的是要越有效率越好，以處理更大量的數據
所以，想一個很大的數字當作 \(n\) 吧
以 \(2^{31}\) 為例好了
\(x\ \ \ \ \ \ \ \approx 2.1 \cdot 10^9\)
\(x + 1 \approx 2.1 \cdot 10^9\)
基本上沒什麼差別
所以在複雜度中， \(x + 1 = x\)
看數字
演算法的目的是要越有效率越好，以處理更大量的數據
所以，想一個很大的數字當作 \(n\) 吧
以 \(2^{31}\) 為例好了
\(x\ \ \ \ \ \ \ \approx 2.1 \cdot 10^9\)
\(x + 1 \approx 2.1 \cdot 10^9\)
\(\ \ x \approx 2.1 \cdot 10^9\)
\(3x \approx 6.4 \cdot 10^9\)
基本上沒什麼差別
所以在複雜度中， \(x + 1 = x\)
差了 \(3\) 倍欸
\(x^2 \approx 4.6 \cdot 10^{18}\)
差了大概 \( 10^{9}\) 倍！
相較之下 \(3\) 倍似乎不算什麼了
所以在複雜度中， \(3x = x\)
大 \(O\) 符號
在表示複雜度時把所有常數和係數忽略
\(\Rightarrow O(x^3)\)
要做 \( 8x^3 + 2x^2 + x + log_2(x) + 256 \) 件事
\(\Rightarrow O(x\ log\ x)\)
要做 \( 4x \cdot log_2(x) \) 件事
貪婪 Greedy
不是得寸進尺、貪得無厭的感覺啦
AaW 與他的能量藥水
有一位製藥機器人 AaW 他可以釀出不同效果的藥水
但今天他一直電別人，導致電力不足，於是今天的藥水品質不一
有的會讓你很有精神，有的會直接讓你昏倒
現在你知道第 \(i\) 杯藥水喝下去會得到的能量為 \(e_i\)
\(\ e_i \in [-128, 128)\)
若你可以選擇要喝哪些，則最多能得到多少能量？
就把能量為正的全都喝掉就好啦
此故事來自 AaW 的簡報
寫成 Code 來看
#include <iostream>
#include <vector>
int main() {
// there are n bottles of potion
int n;
std::cin >> n;
// a vector to store the energy content of each potion
std::vector<int> potions;
// input
for (int& p : potions)
std::cin >> p;
// a variable to store the sum of all taken energy
int maxEnergy = 0;
// loop through
for (int& p : potions)
if (p > 0)
maxEnergy += p;
// print the result
std::cout << maxEnergy;
}輸入的順序
輸入的順序很重要，不然就會輸入錯的變數
假設這題的順序為 \(n \rightarrow e_1 \rightarrow e_2 \rightarrow e_3 \rightarrow ... \rightarrow e_{n-1} \rightarrow e_n\)
n
e_1 e_2 e_3 e_4 e_5 ... e_n你可能會覺得這樣很噁心
只有一堆數字，都沒有 UI
但沒辦法，我們得要有標準答案，不要太多變化
換成比較好理解的方式會長這樣：
題外話
所以什麼是貪婪
無論如何都選擇目前看起來比較好的！
以 AaW 的藥水為例，只拿帶正能量的
希望這個作法可以讓最後的結果最好！
但是使用前要先想一想，這個題目真的是要使用貪婪嗎？
使用貪婪的時機：
- 你可以證明沒有更好的做法
- 用數學歸納法或反證法
但基本上沒有人會去證明它
複雜度
以 AaW 的藥水為例
如果把所有可能都考慮一遍
那就是 \(O(2^n)\)
如果直接貪婪起來
那就是 \(O(n)\)
但我知道拿這個例子來討論複雜度好像沒什麼意義
二分搜
切一半，然後再切一半
晴☆與他的程式
有一天，晴☆在寫程式，但他發現他寫的程式爛掉了
原來是出現了某個 Bug！
不過晴☆有個好習慣，他會把每一個版本都備份
於是就可以回去找這個 Bug 是哪個版本開始出現的
但他發現他目前有 10000 個版本，開始往回翻最多要翻 10000 次
晴☆在找到 Bug 之前可能會先睡著
那我們使用二分搜好了
開始囉！
\(1\)
\(10000\)
Bug 出現
有 Bug
\(5000\)
Step 1
\(1\)
\(10000\)
Bug 出現
沒有 Bug
\(2500\)
Step 2
\(1\)
\(10000\)
Bug 出現
有 Bug
\(3750\)
Step 3
\(1\)
\(10000\)
Bug 出現
沒有 Bug
\(3125\)
Step 4
\(1\)
\(10000\)
Bug 出現
快速地接近目標了！
不過事實上的我是這樣
\(1\)
\(10000\)
Bug 出現
不過事實上的我是這樣
這是需要做最多次的情況之一
複雜度
從第 10000 個版本開始一個一個往前找
複雜度為 \(O(n)\)
使用二分搜
因為每次都切一半
所以最多只要做 \(log_2(n)\) 次
複雜度為 \(O(log\ n)\)
寶妮題目
小寶與小妮又出現了
寶妮老師與她的邪教儀式
你加入了某個邪教
今天就是獻祭儀式的日子了
是這樣的，所有人圍成一圈，並編號 \(1 \sim 100\)
接著從 \(1\) 號開始，每個人砍死右手邊的人
然後最後一個人舉刀自殺
儀式開始前，你忽然清醒並發現這是個邪教
但是你是無法退出邪教的
於是你想成為那最後一個人，然後逃走
沒聽懂？畫個圖
寶妮老師與她的邪教儀式
你加入了某個邪教
今天就是獻祭儀式的日子了
是這樣的，所有人圍成一圈，並編號 \(1 \sim 100\)
接著從 \(1\) 號開始，每個人砍死右手邊的人
然後最後一個人舉刀自殺
儀式開始前，你忽然清醒並發現這是個邪教
但是你是無法退出邪教的
於是你想成為那最後一個人，然後逃走
沒聽懂？畫個圖
1
2
3
4
5
寶妮老師與她的邪教儀式
2
1
5
4
3
寶妮老師與她的邪教儀式
1
5
4
3
寶妮老師與她的邪教儀式
1
5
3
寶妮老師與她的邪教儀式
5
3
寶妮老師與她的邪教儀式
3
活下來的是 \(3\) 號
寶妮老師與她的邪教儀式
3
今天有 \(100\) 位教徒（包括你自己）
你應該要是第幾號才能最後生存下來並逃走呢？
活下來的是 \(3\) 號
演算法
By 晴☆
