Deep Learning
Grundlagen

Dr. Stefan Hackstein
stefan.hackstein@fhnw.ch
Deep Learning
Grundlagen

Slides
Machine Learning
vs Deep Learning
Machine Learning
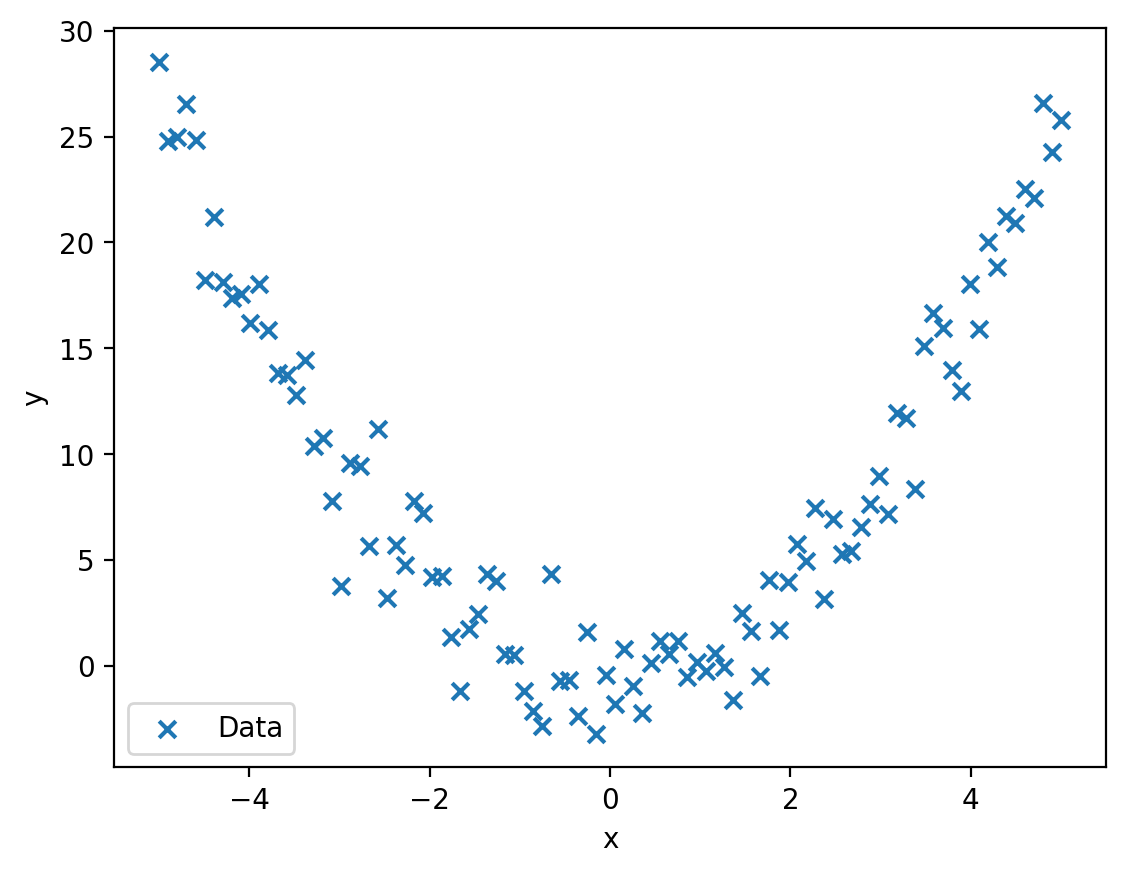
Text
Strukturen in Daten finden
Machine Learning

Lineare Regression
Machine Learning

Machine Learning
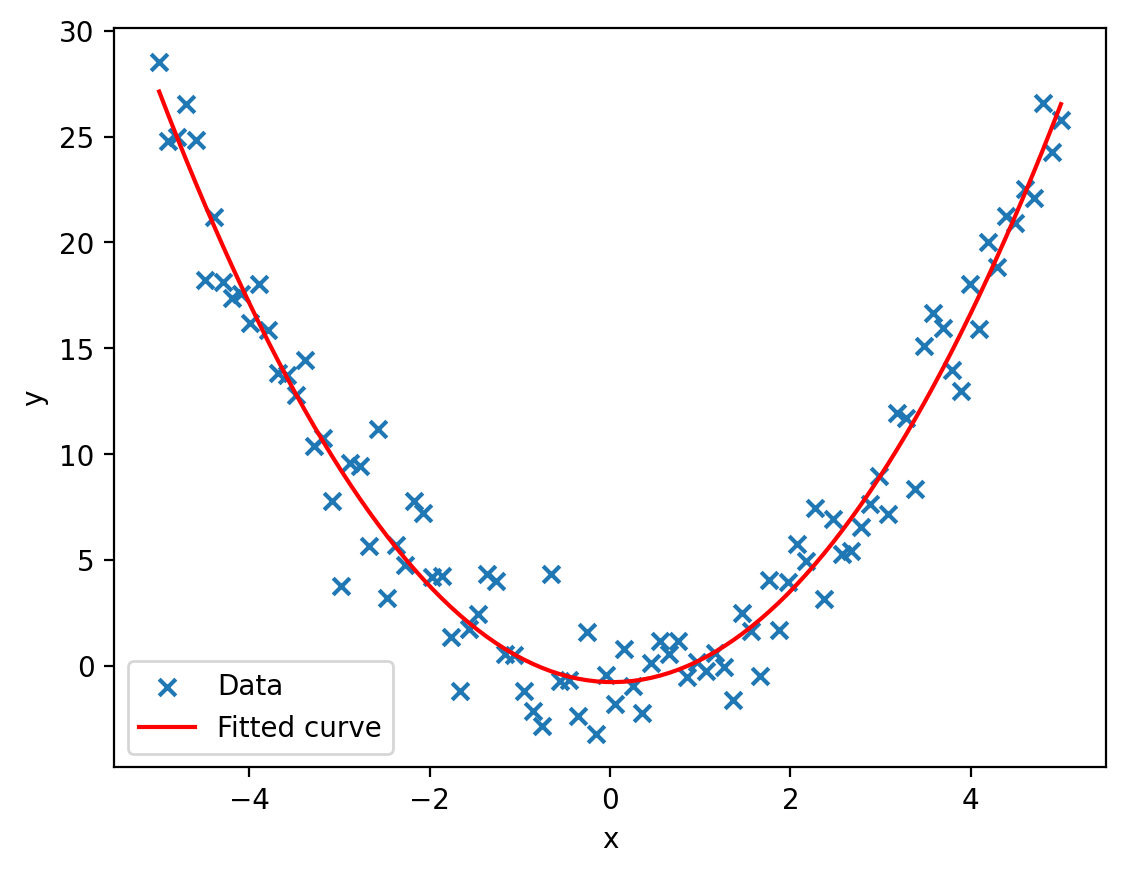
Machine Learning

- Genereller Funktionsapproximator
- braucht geeignete Basisfunktionen
- braucht kuratierte Daten

Machine Learning

Machine Learning
Deep Learning

Deep Learning

Deep Learning
-
Universeller Funktionsapproximator
- Findet Basisfunktionen selbst
Deep Learning
-
Findet Basisfunktionen selbst
mit Linearer Regression
Deep Learning
-
Findet Basisfunktionen selbst
mit Linearer Regression
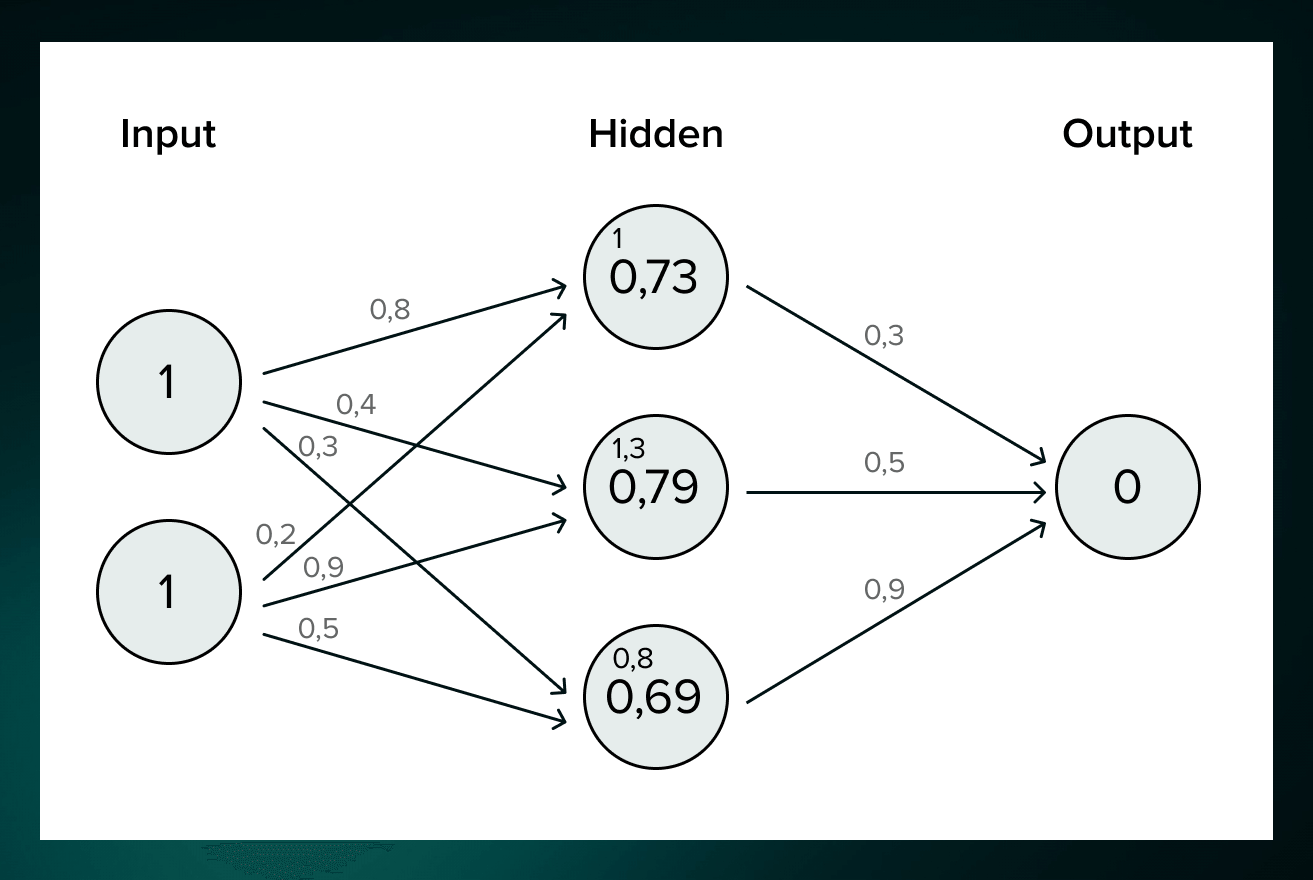
Deep Learning
-
Findet Basisfunktionen selbst
mit Linearer Regression

Weights * Inputs + Bias
Deep Learning
-
Findet Basisfunktionen selbst
mit Linearer Regression
Weights * Inputs + Bias
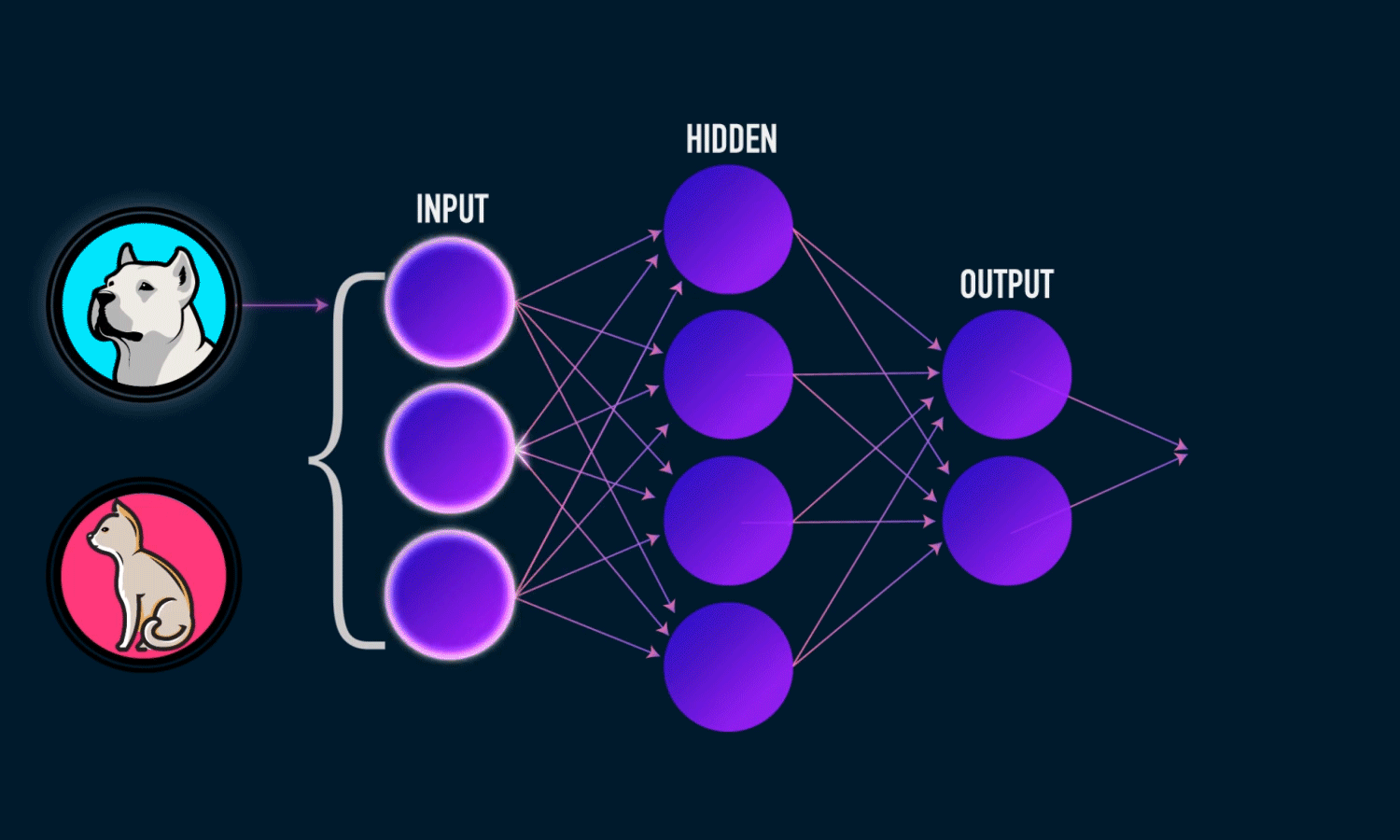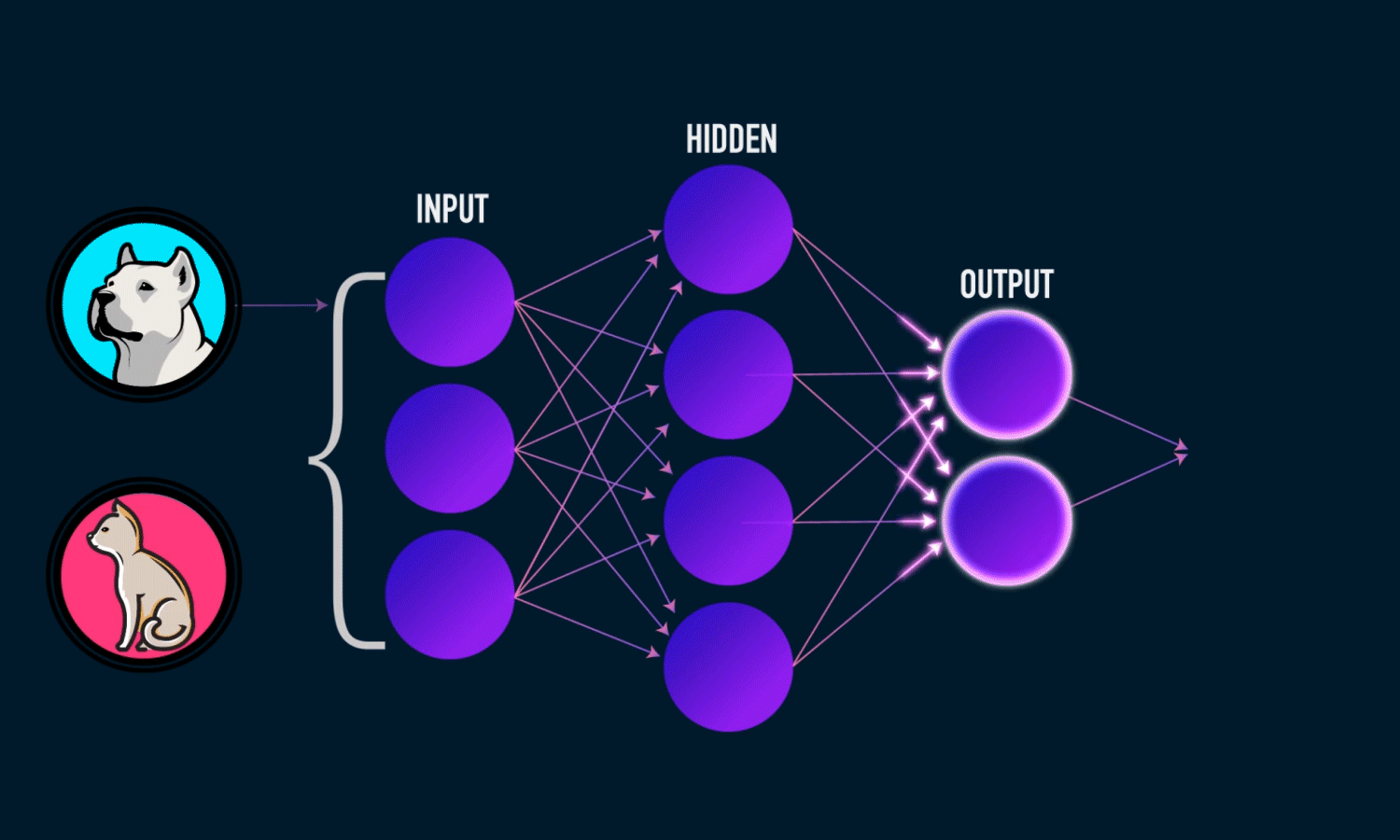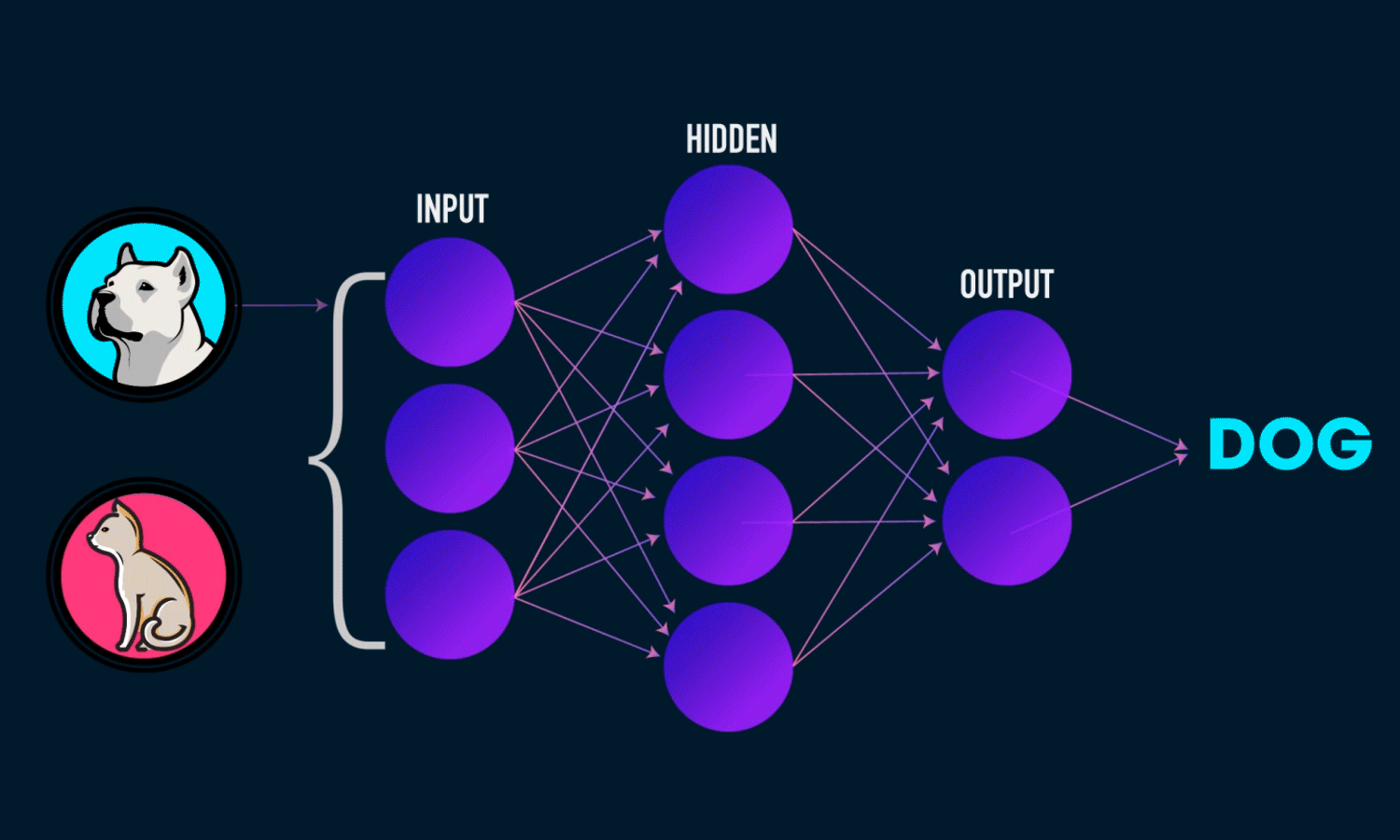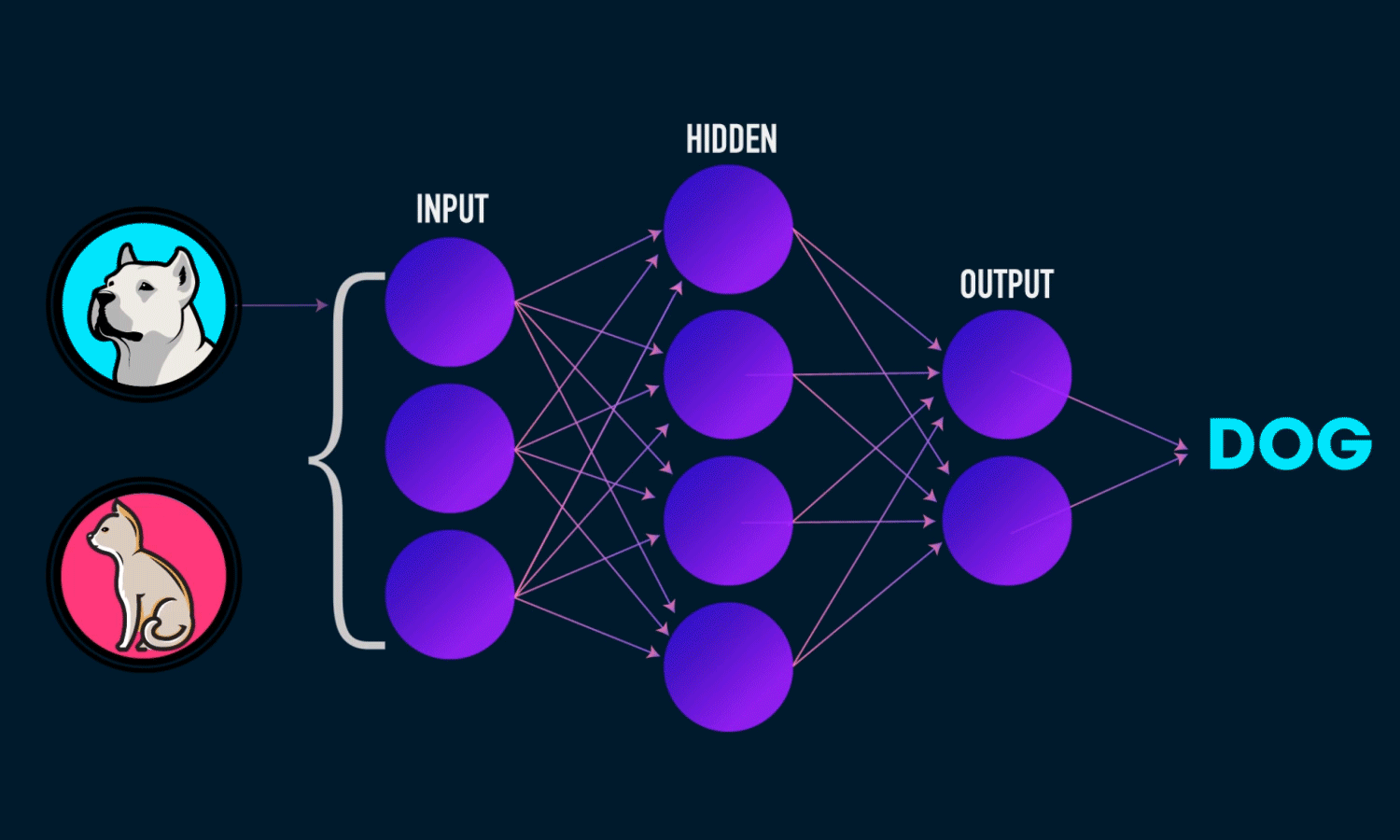
Deep Learning
- Spezialgebiet des Machine Learning
Deep Learning
- Spezialgebiet des Machine Learning
- Universeller Funktionsapproximator: Neuronale Netze
Deep Learning
- Spezialgebiet des Machine Learning
- Universeller Funktionsapproximator: Neuronale Netze
- Komplexe Algorithmen
Deep Learning
- Spezialgebiet des Machine Learning
- Universeller Funktionsapproximator: Neuronale Netze
- Komplexe Algorithmen
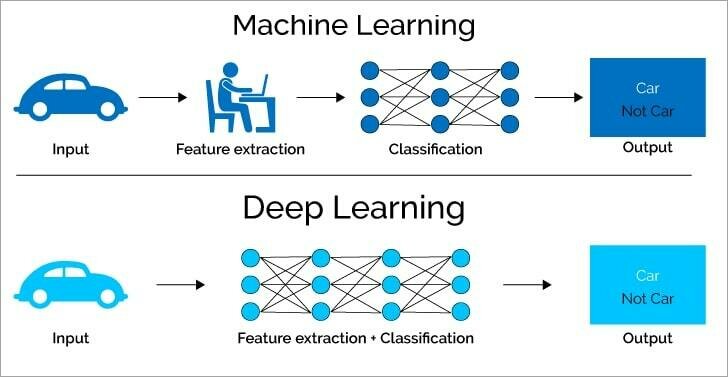
Deep Learning
Anwendungen
Deep Learning
Anwendungen
-
Computer Vision: Klassifizierung, Objekterkennung, Bildgenerierung
(16.09., 30.09. & 28.10. Amadeus Oertel) -
Natural Language Processing: Übersetzungen, Chatbots
(22.09., 29.09. & 20.10. Fabian Märki & Joel Akaret) -
Reinforcement Learning: Gaming, Robotik, Automatisierung
(10.11. Yanick Schraner) -
Zeitreihenanalyse: Markt- & Wetterprognosen, Anomalieerkennung
(03.11. Fernando Benites) -
Explainable AI: Transparenz, Vertrauen, Sicherheit
(04.11., 17.11. & 08.12. Susanne Suter)
Deep Learning
Good Practice
-
Daten Erkunden
-
Modell & Trainingsloop erstellen
-
Overfitten
-
Regularisieren
-
Optimieren
-
Evaluieren
Daten Erkunden
Daten Erkunden
- Verstehen: Inhalt, Format, Label, Metadaten
Daten Erkunden
- Verstehen: Inhalt, Format, Label, Metadaten
- Visualisieren: Verteilung, Korrelation, Ausreisser
Daten Erkunden
- Verstehen: Inhalt, Format, Label, Metadaten
- Visualisieren: Verteilung, Korrelation, Ausreisser
- Preprocessing: normalisieren, skalieren, enkodieren, balancieren
Daten Erkunden
Hands-On: MNIST Datensatz
Öffnen sie dieses Notebook und bearbeiten Sie die Aufgaben. Beantworten Sie so folgende Fragen:
- Welche Daten enthält der Datensatz?
- Welches Format haben die Daten?
- Welche Klassen gibt es und wie sind diese Verteilt?
- Wie machen wir die Klassen dem Modell verständlich?
- Welche Skalierung der Daten ist sinnvoll?
Die Lösung finden Sie in diesem Notebook
Daten Erkunden
Hands-On: MNIST Datensatz
Welche Daten enthält der Datensatz?
data.shape -> (N_data, size_input)Die shape eines Datensatzes zeigt die Anzahl der Elemente (N_data) sowie das format der einzelnen Elemente (size_input)
Daten Erkunden
Hands-On: MNIST Datensatz
Welches Format haben die Daten?
Die type(x) Funktion gibt die Klasse von x an
type(data[0]) -> classDie built-in Funktion x.dtype gibt den Datentyp von x an
data.dtype -> data_typeDaten Erkunden
Hands-On: MNIST Datensatz
Welche Klassen gibt es und wie sind diese Verteilt?
numpy.unique(x) liefert eine liste aller Elemente die in x vorkommen
labels = np.unique(target)numpy.bincount(x) liefert die Anzahl von Integerwerten in x, geordnet nach Zahlenwert der Integer
counts = np.bincount(target.astype(int))Daten Erkunden
Hands-On: MNIST Datensatz
Wie machen wir die Klassen dem Modell verständlich?
Um Stringlabel in für das Modell verständliche Floats zu verwandeln nutzen wir One-Hot-Encoding
# zB "3" -> [0,0,0,1,0,0,0,0,0,0]
#
from sklearn.preprocessing import OneHotEncoder
encoder = OneHotEncoder()
labels = encoder.fit_transform(target)Die letzte Zeile erwartet target mit shape (N,1)
Daten Erkunden
Hands-On: MNIST Datensatz
Welche Skalierung der Daten ist sinnvoll?
In den Knoten eines Neuronalen Netzes werden viele Werte aufsummiert, was zu sehr grossen Ergebnissen führen kann.
Ausserdem haben grundsätzlich hohe Features ein stärkeres Gewicht.
Um das zu verhindern werden die Input-Daten auf [-1,1] skaliert.
Dazu benutzt man idR das Min-Max scaling
scaled_data = (data - np.min(data)) / (np.max(data) - np.min(data)) * 2 - 1
Modell & Trainingsloop
Modell
Deep Learning Modell = Neuronales Netz
Neuronales Netz = einfache Dartstellung sehr komplizierter Rechnung
LinReg mit Basisfunktionen aus LinReg mit Basis...

Layer
Layer = Level für Lineare Regression
Mehrere Knoten (Perceptronen)
Knoten = gewichtete Summe & Aktivierungsfunktion
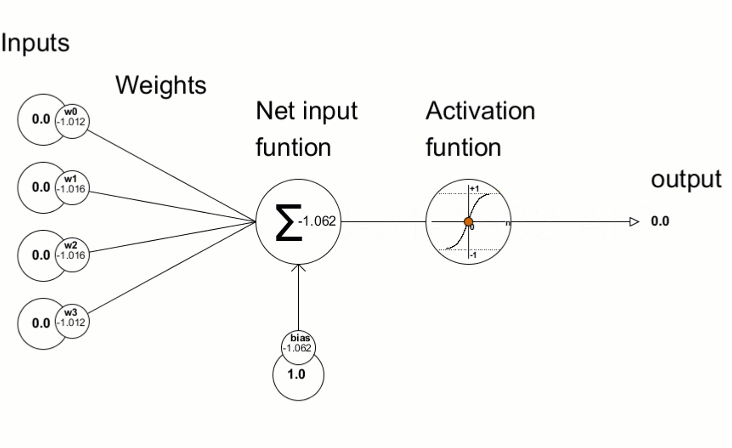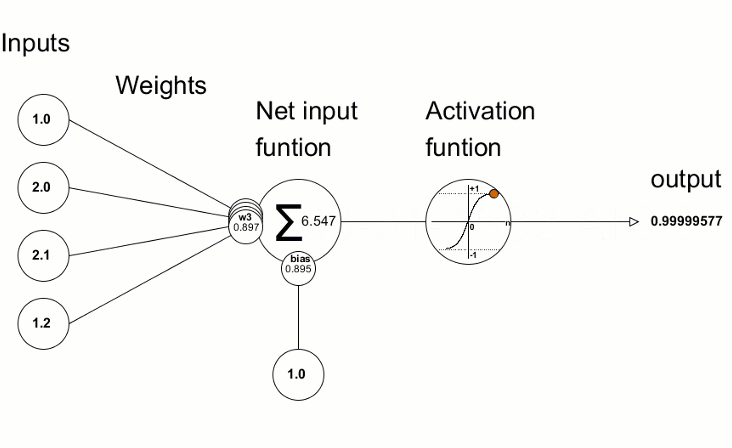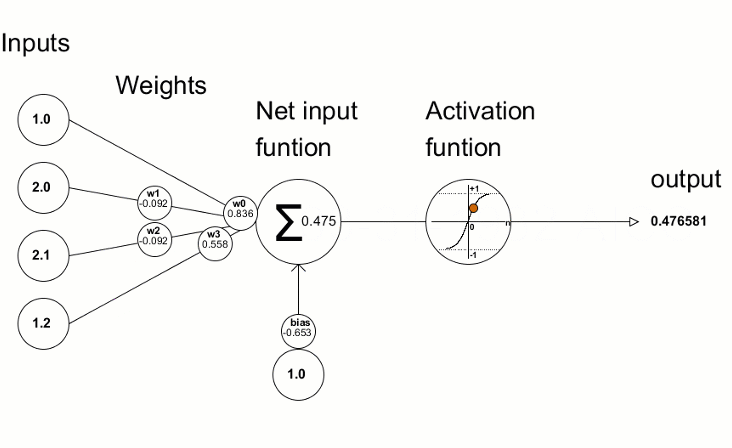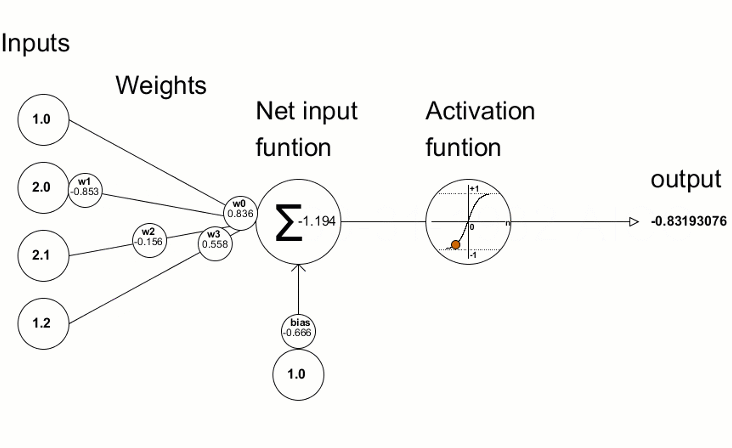
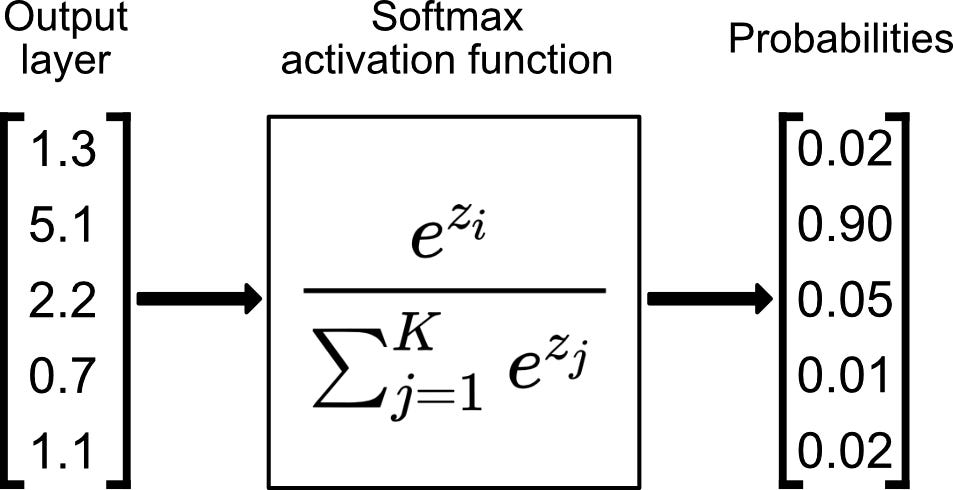
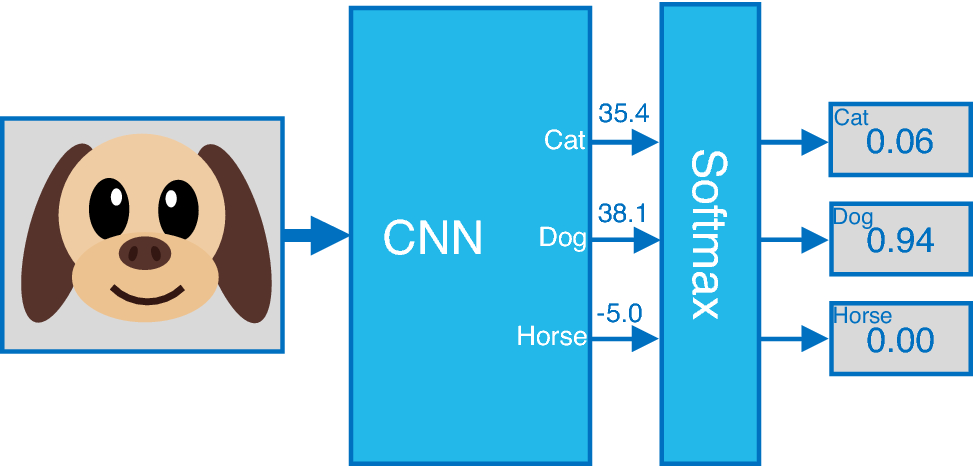
Aktivierungsfunktion
Wahl der Aktivierung:
- Hidden: Effizienz (ReLU)
- Output: Wertebereich Target
Aktivierungsfunktion
Architektur entwerfen
- Aufgabe klar definieren (Klassifikation, Regression, Erkennung, ...)
- Ein- und Ausgabedimension festlegen (MNIST: In: 784; Out: 10)
- Geeignete Art von Schichten bestimmen (Linear, Convolutional, ...)
- Anzahl Schichten und Neuronen pro Schicht festlegen
- Aktivierungsfunktionen festlegen (Hidden & Output)
Implementation
from torch import nn
import torch.nn.functional as F
class Classifier(nn.Module):
def __init__(self):
super().__init__()
self.fc1 = nn.Linear(784, 256)
self.fc2 = nn.Linear(256, 128)
self.fc3 = nn.Linear(128, 64)
self.fc4 = nn.Linear(64, 10)
def forward(self, x):
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
x = F.relu(self.fc3(x))
x = F.softmax(self.fc4(x), dim=1)
return x
model = Classifier()
output = model(data)
Pytorch (Meta)
import tensorflow as tf
from tensorflow.keras import layers
class Classifier(tf.keras.Model):
def __init__(self):
super(Classifier, self).__init__()
self.fc1 = layers.Dense(256, activation='relu')
self.fc2 = layers.Dense(128, activation='relu')
self.fc3 = layers.Dense(64, activation='relu')
self.fc4 = layers.Dense(10, activation='softmax')
def call(self, x):
x = self.fc1(x)
x = self.fc2(x)
x = self.fc3(x)
x = self.fc4(x)
return x
model = Classifier()
model.build((None, 784))
output = model(data)
Tensorflow (Google)
- MNIST Classifier
- 10 Outputs
- 2 Hidden Layer
- Softmax activation
Implementation
import torch.nn as nn
model = nn.Sequential(
nn.Linear(784, 256),
nn.ReLU(),
nn.Linear(256, 128),
nn.ReLU(),
nn.Linear(128, 64),
nn.ReLU(),
nn.Linear(64, 10),
nn.Softmax(dim=1)
)
output = model(data)
Pytorch (Meta)
from tensorflow.keras import models
model = models.Sequential([
layers.Dense(256, activation='relu', input_shape=(784,)),
layers.Dense(128, activation='relu'),
layers.Dense(64, activation='relu'),
layers.Dense(10, activation='softmax')
])
output = model(data)
Tensorflow (Google)
- MNIST Classifier
- 10 Outputs
- 2 Hidden Layer
- Softmax activation
Implementation
Pytorch
- Gentle learning curve
- More Pythonic
- Research-oriented
Tensorflow
- Steep learning curve
- Multi-Language support
- Production-oriented
Beide Frameworks sehr nützlich & weit verbreitet
Mathematik identisch & Aufbau sehr ähnlich
Wahl meist durch Arbeitsumfeld bestimmt
Trainingsloop
- Daten laden (batch)
- Modell anwenden (forward)
- Loss berechnen
- Updates berechnen (backward)
- Update durchfüren
Trainingsloop entwerfen
- Aufgabe klar definieren
- Lossfunktion bestimmen
- Berechnungsschritte definieren
Loss Funktion
- Definiert das Ziel des Trainings
- Ziel: Loss minimieren
- erlaubt Vergleich von Modellen
- verschiedene Losses für verschiedene Aufgaben
Loss Funktion
- Mean Squared Error (MSE):
mittlerer quadratische Abweichung
- Binare Cross-Entropy (BCE):
vergleich von Wahrscheinlichkeit einer Klasse
- Cross-Entropy (CE):
vergleich von Wahrscheinlichkeiten mehrerer Klassen
Update

Loss -> Ableitung -> Richtung für Verbesserung -> Update
Implementation
criterion = nn.CrossEntropyLoss()
optimizer = optim.Adam(model.parameters(), lr=0.003)
for e in range(epochs):
running_loss = 0
for images, labels in trainloader:
prediction = model(images)
loss = criterion(prediction, labels)
optimizer.zero_grad()
loss.backward()
optimizer.step()
running_loss += loss.item()Pytorch
- Loss: CrossEntropy
- Optimizer: Adam
model.compile(optimizer=optimizers.Adam(learning_rate=0.003),
loss='sparse_categorical_crossentropy',
metrics=['accuracy'])
history = model.fit(train_images, train_labels, epochs=1, batch_size=64)
print(f'Training loss: {history.history["loss"][0]}')
Tensorflow
Model & Trainingsloop
Hands-On: MNIST Classifier
Bearbeiten Sie eines dieser Notebooks: pytorch, tensorflow.
- Erstellen Sie einen Classifier
- Definieren Sie die Trainingsloop
- Testen Sie Ihre Implementation mit einer Trainingsepoche
Die Lösung finden Sie in diesen Notebooks: pytorch, tensorflow
Deep Learning Grundlagen
By Stefan Hackstein
Deep Learning Grundlagen
- 361



