Deep Learning
Grundlagen

Dr. Stefan Hackstein
stefan.hackstein@fhnw.ch
Deep Learning
Abschlusstag: 12. Januar, Vormittags?
Deep Learning
Grundlagen
Machine Learning
Deep Learning


Machine Learning
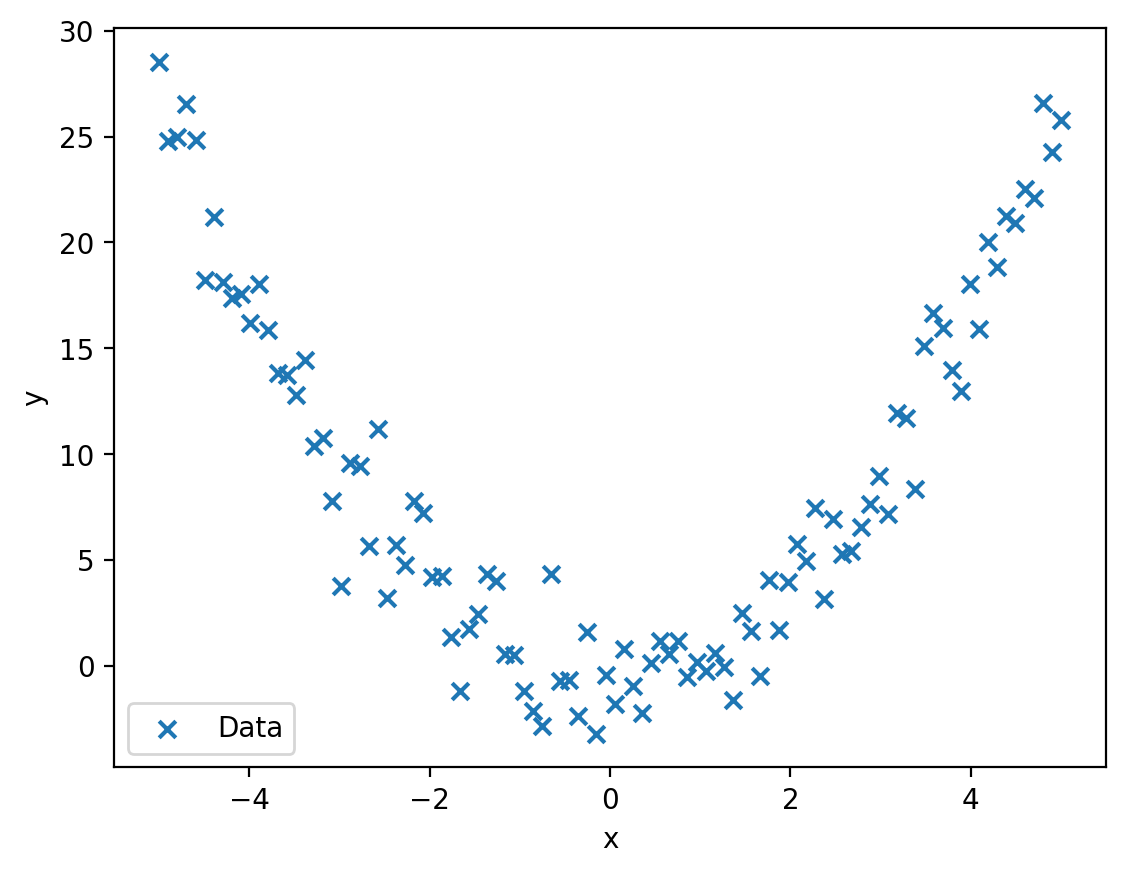
Strukturen in Daten finden
Machine Learning
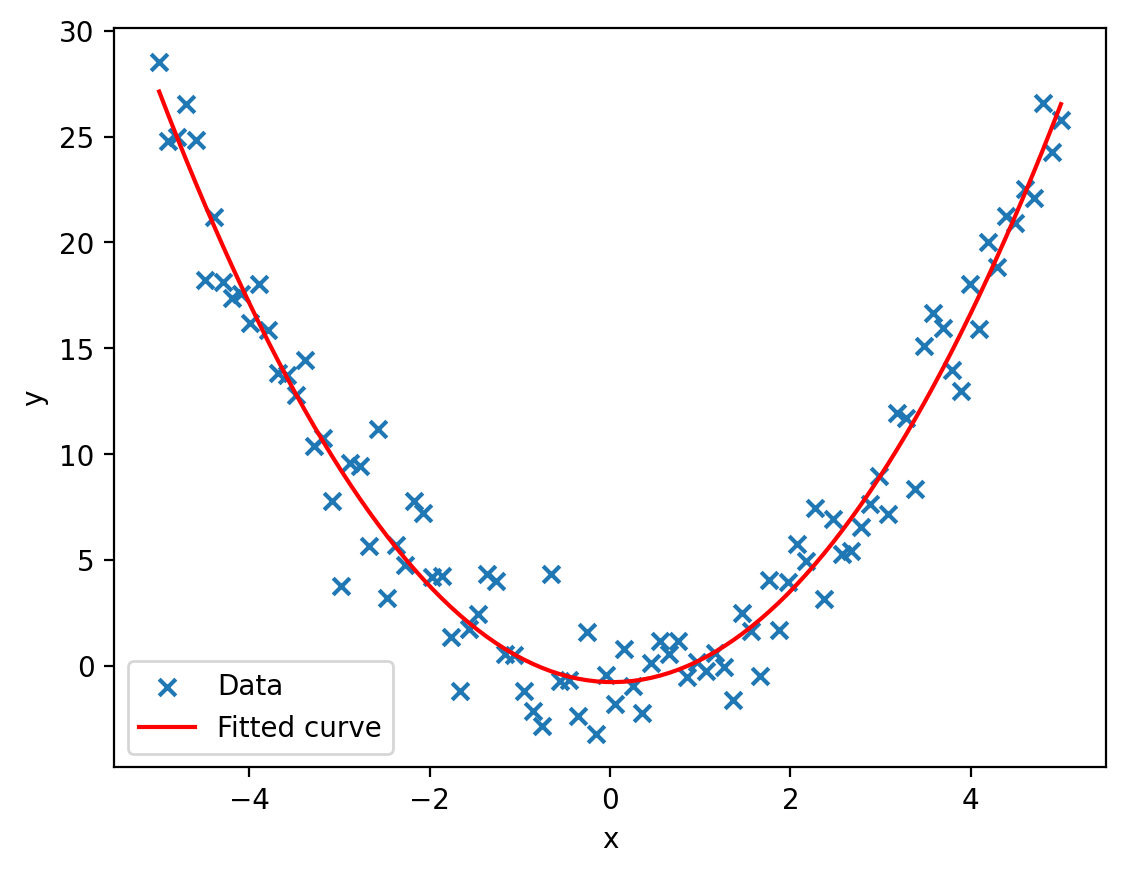
Lineare Regression
Machine Learning

- Genereller Funktionsapproximator
- braucht geeignete Basisfunktionen
- braucht kuratierte Daten
Lineare Regression

Machine Learning

Machine Learning
Deep Learning

Deep Learning

Deep Learning
-
Universeller Funktionsapproximator
- Findet Basisfunktionen selbst?
Deep Learning
-
Findet Basisfunktionen selbst
mit Linearer Regression
Deep Learning
-
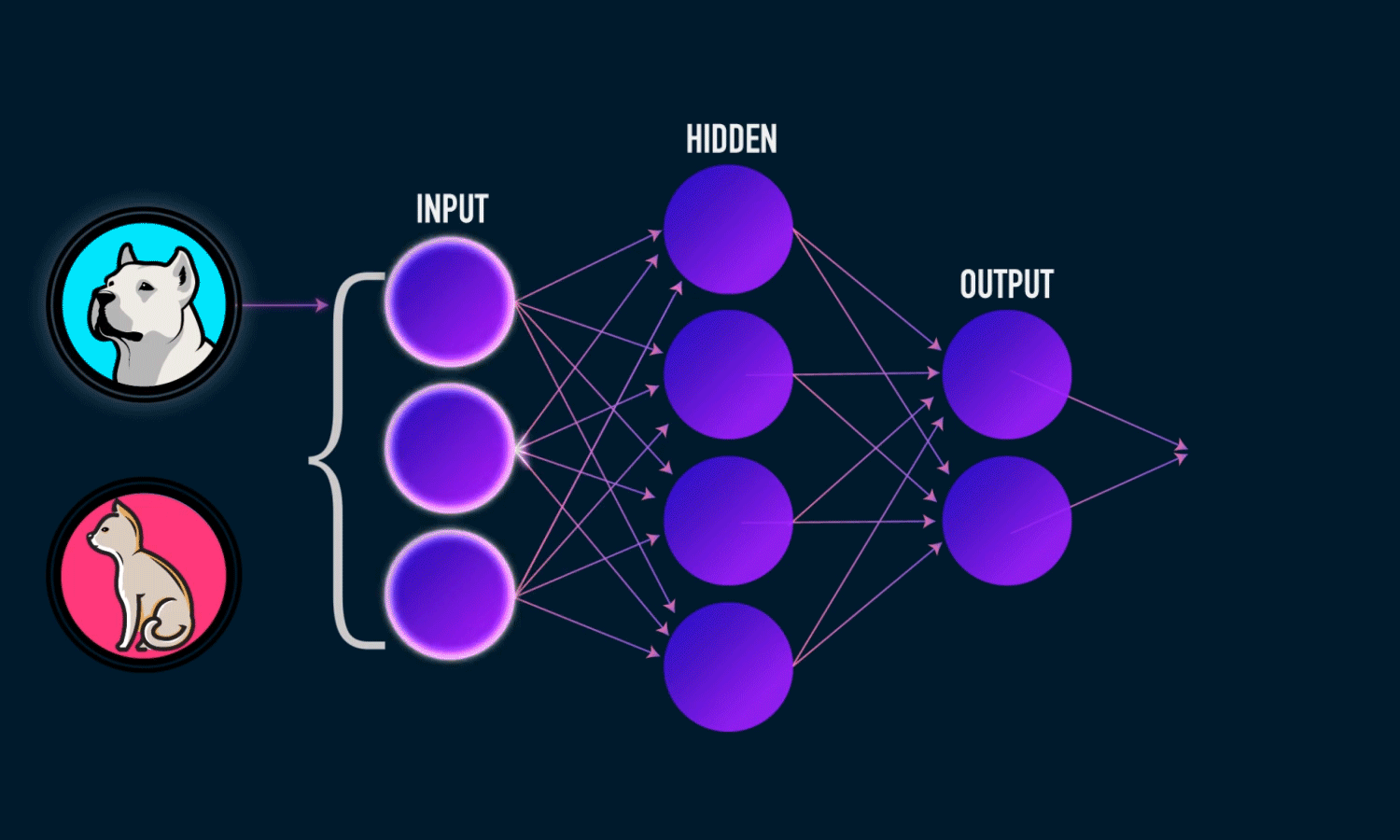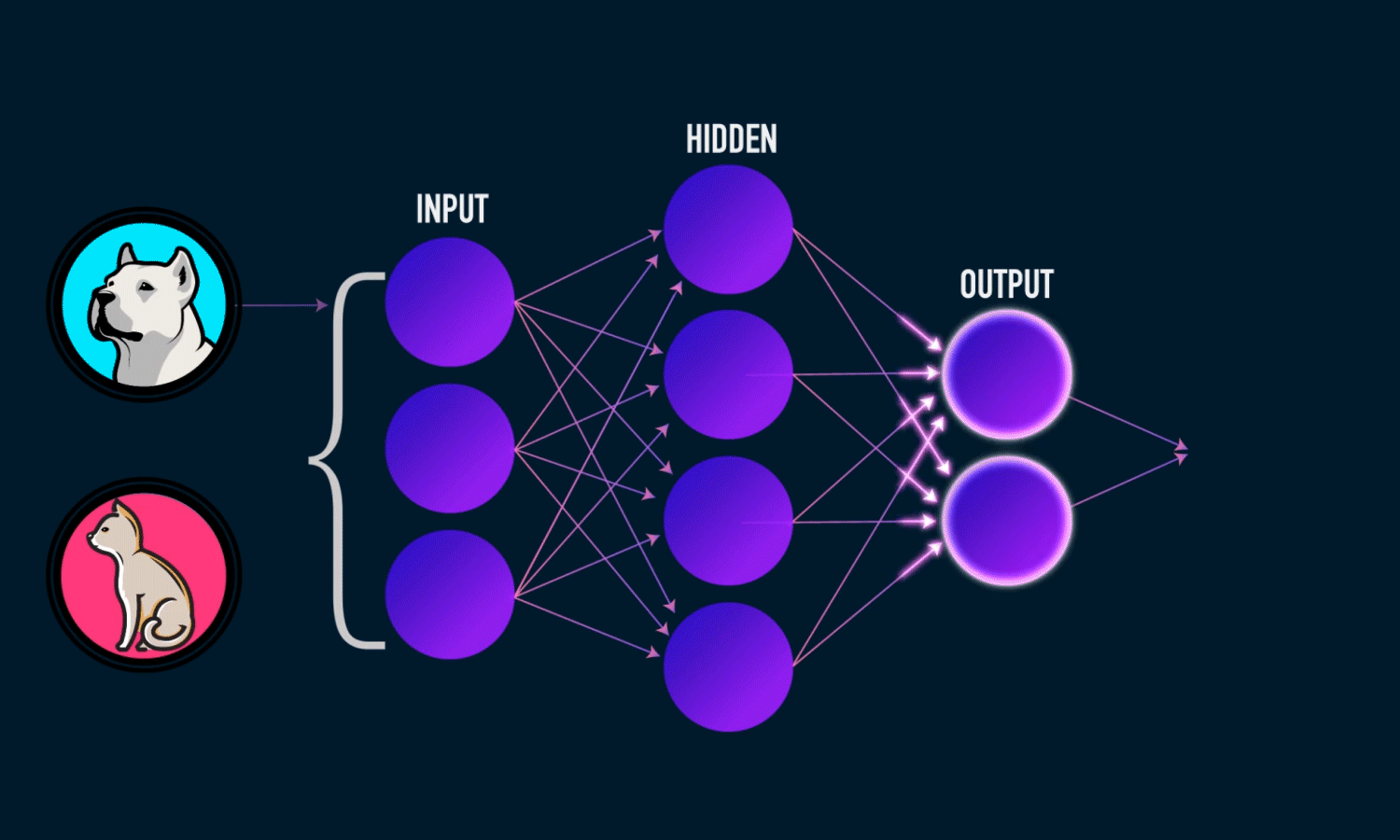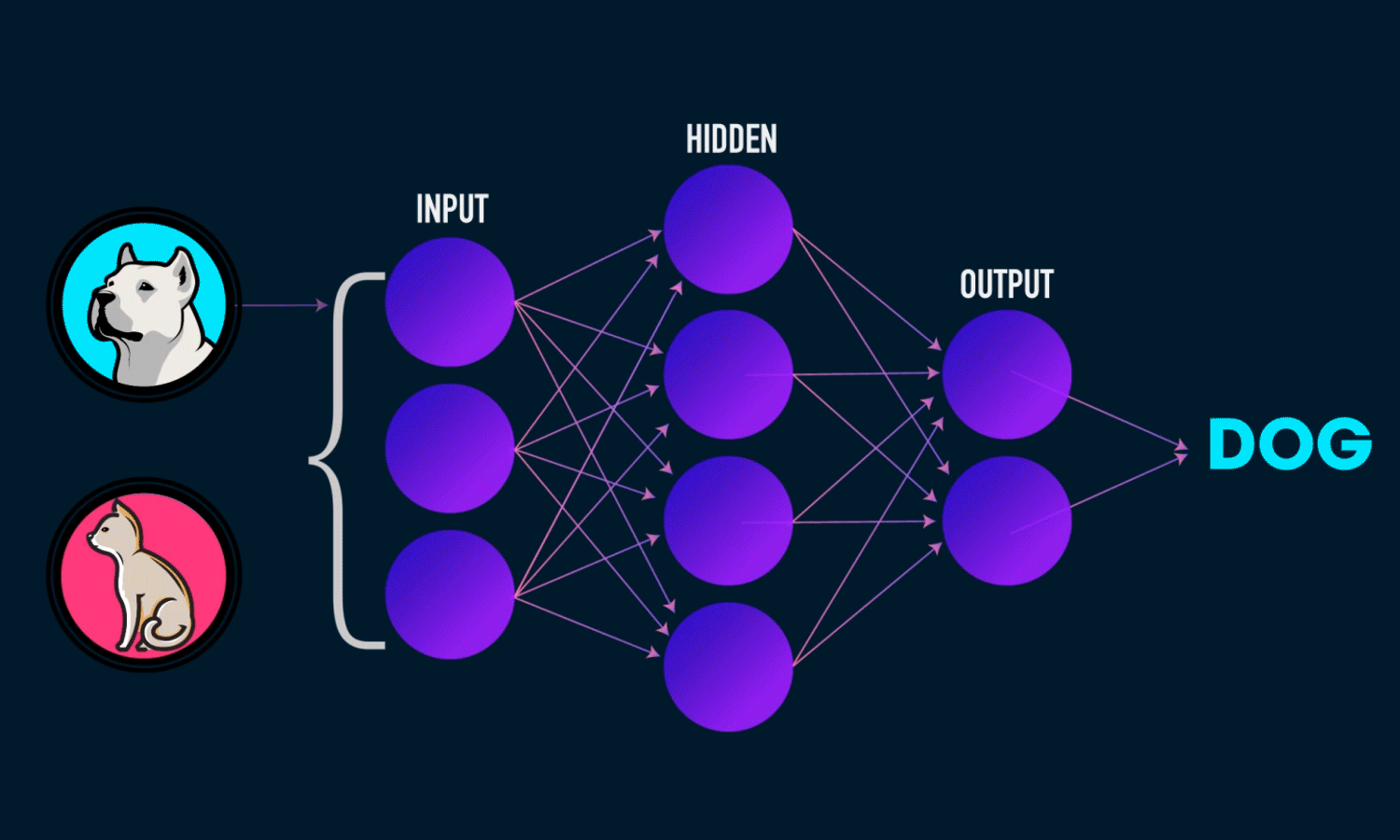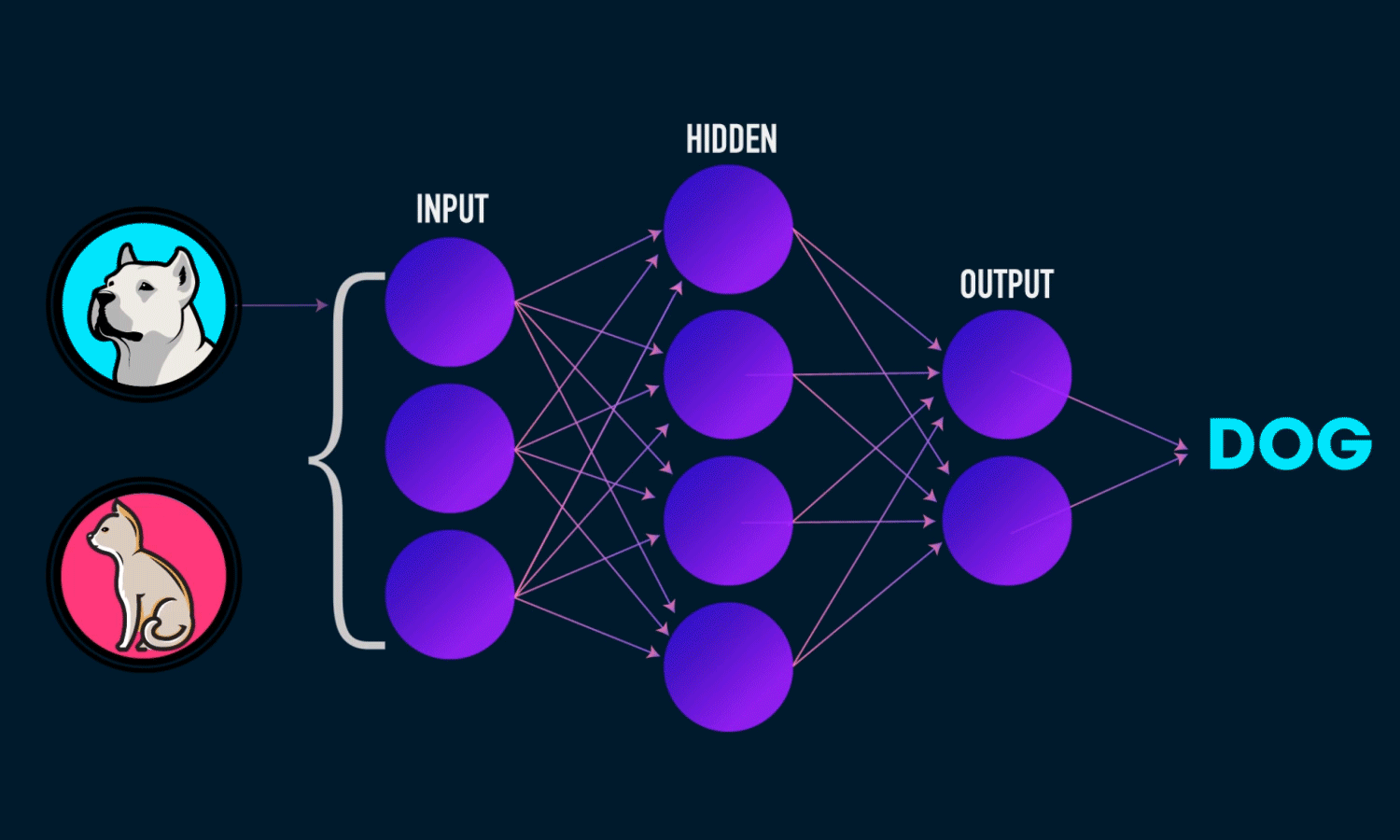
Findet Basisfunktionen selbst
mit Linearer Regression
Output Layer
Hidden Layers
Input Layer
Deep Learning
-
Findet Basisfunktionen selbst
mit Linearer Regression
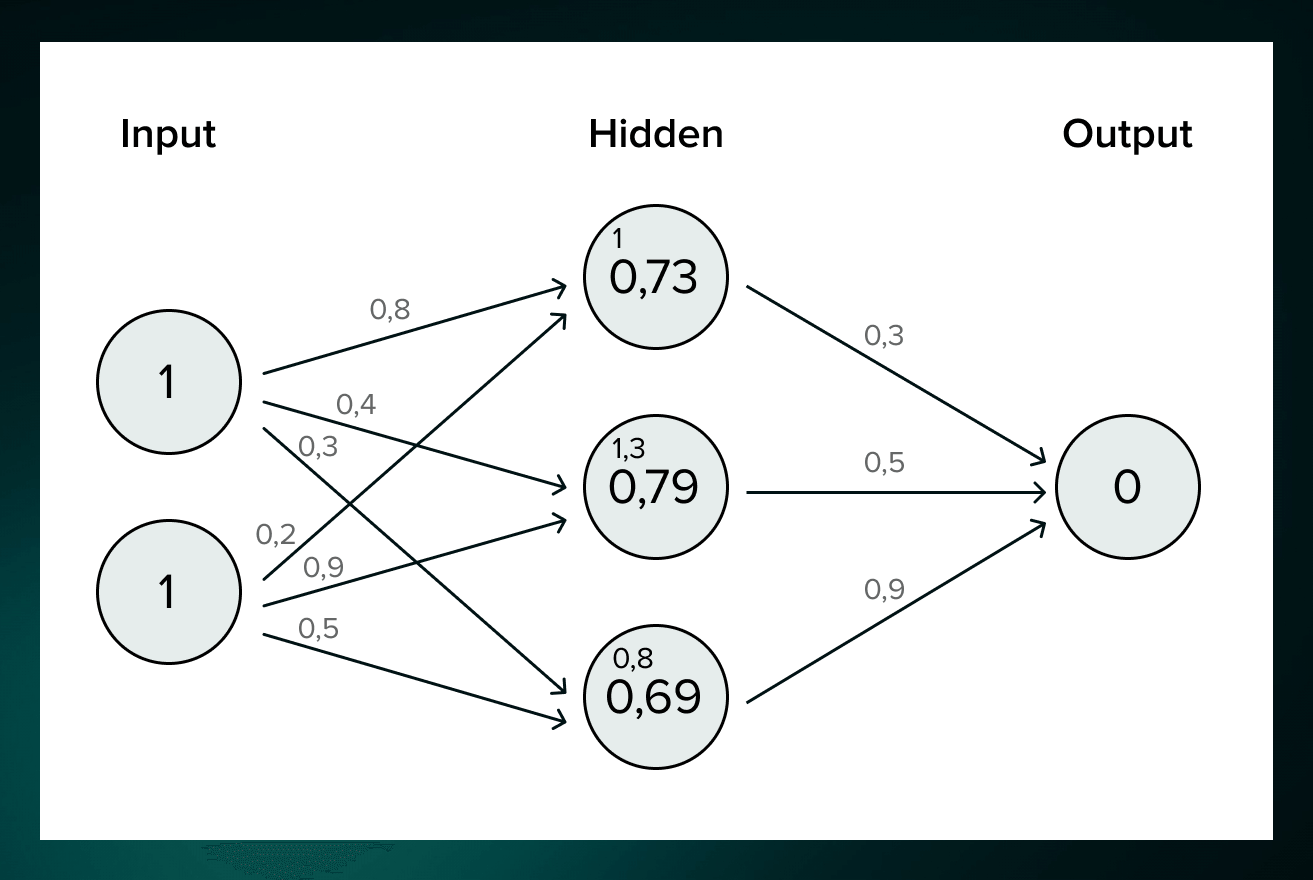
Weights * Inputs + Bias
Deep Learning
-
Findet Basisfunktionen selbst
mit Linearer Regression
Weights * Inputs + Bias
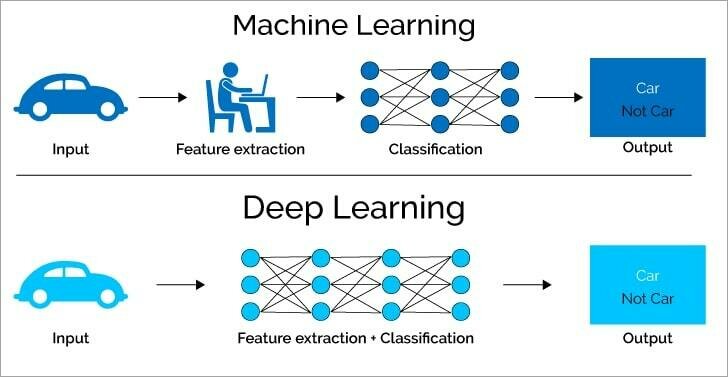
Deep Learning
- Spezialgebiet des Machine Learning
- Universeller Funktionsapproximator: Neuronale Netze
- Komplexe Algorithmen
Deep Learning
Anwendungen
-
Computer Vision: Klassifizierung, Objekterkennung, Bildgenerierung
-
Natural Language Processing: Übersetzungen, Chatbots
-
Reinforcement Learning: Gaming, Robotik, Automatisierung
-
Zeitreihenanalyse: Markt- & Wetterprognosen, Anomalieerkennung
-
Explainable AI: Transparenz, Vertrauen, Sicherheit
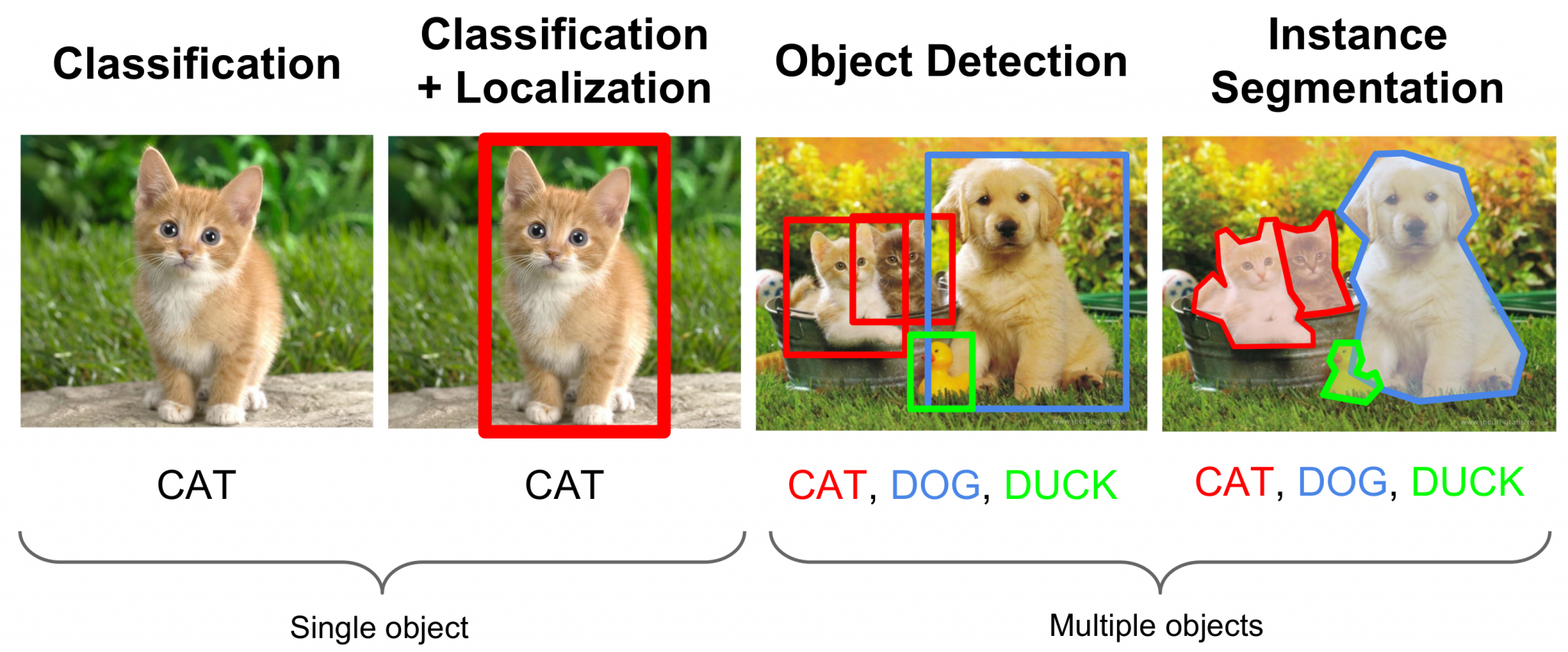
Deep Learning
Anwendungen
-
Computer Vision: Klassifizierung, Objekterkennung, Bildgenerierung
Deep Learning
Anwendungen
-
Computer Vision: Klassifizierung, Objekterkennung, Bildgenerierung

Deep Learning
Anwendungen
-
Computer Vision: Klassifizierung, Objekterkennung, Bildgenerierung
-
Natural Language Processing: Übersetzungen, Chatbots
-
Reinforcement Learning: Gaming, Robotik, Automatisierung
-
Zeitreihenanalyse: Markt- & Wetterprognosen, Anomalieerkennung
-
Explainable AI: Transparenz, Vertrauen, Sicherheit
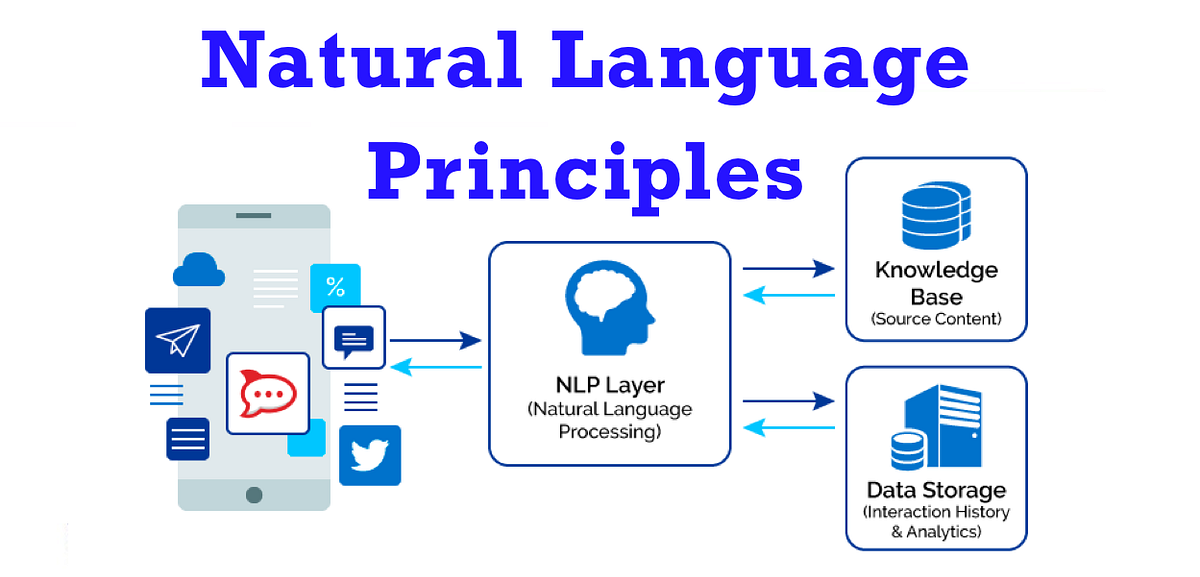
Deep Learning
Anwendungen
-
Natural Language Processing: Übersetzungen, Chatbots

Deep Learning
Anwendungen
-
Computer Vision: Klassifizierung, Objekterkennung, Bildgenerierung
-
Natural Language Processing: Übersetzungen, Chatbots
-
Reinforcement Learning: Gaming, Robotik, Automatisierung
-
Zeitreihenanalyse: Markt- & Wetterprognosen, Anomalieerkennung
-
Explainable AI: Transparenz, Vertrauen, Sicherheit
Deep Learning
Anwendungen
-
Reinforcement Learning: Gaming, Robotik, Automatisierung

Deep Learning
Anwendungen
-
Computer Vision: Klassifizierung, Objekterkennung, Bildgenerierung
-
Natural Language Processing: Übersetzungen, Chatbots
-
Reinforcement Learning: Gaming, Robotik, Automatisierung
-
Zeitreihenanalyse: Markt- & Wetterprognosen, Anomalieerkennung
-
Explainable AI: Transparenz, Vertrauen, Sicherheit
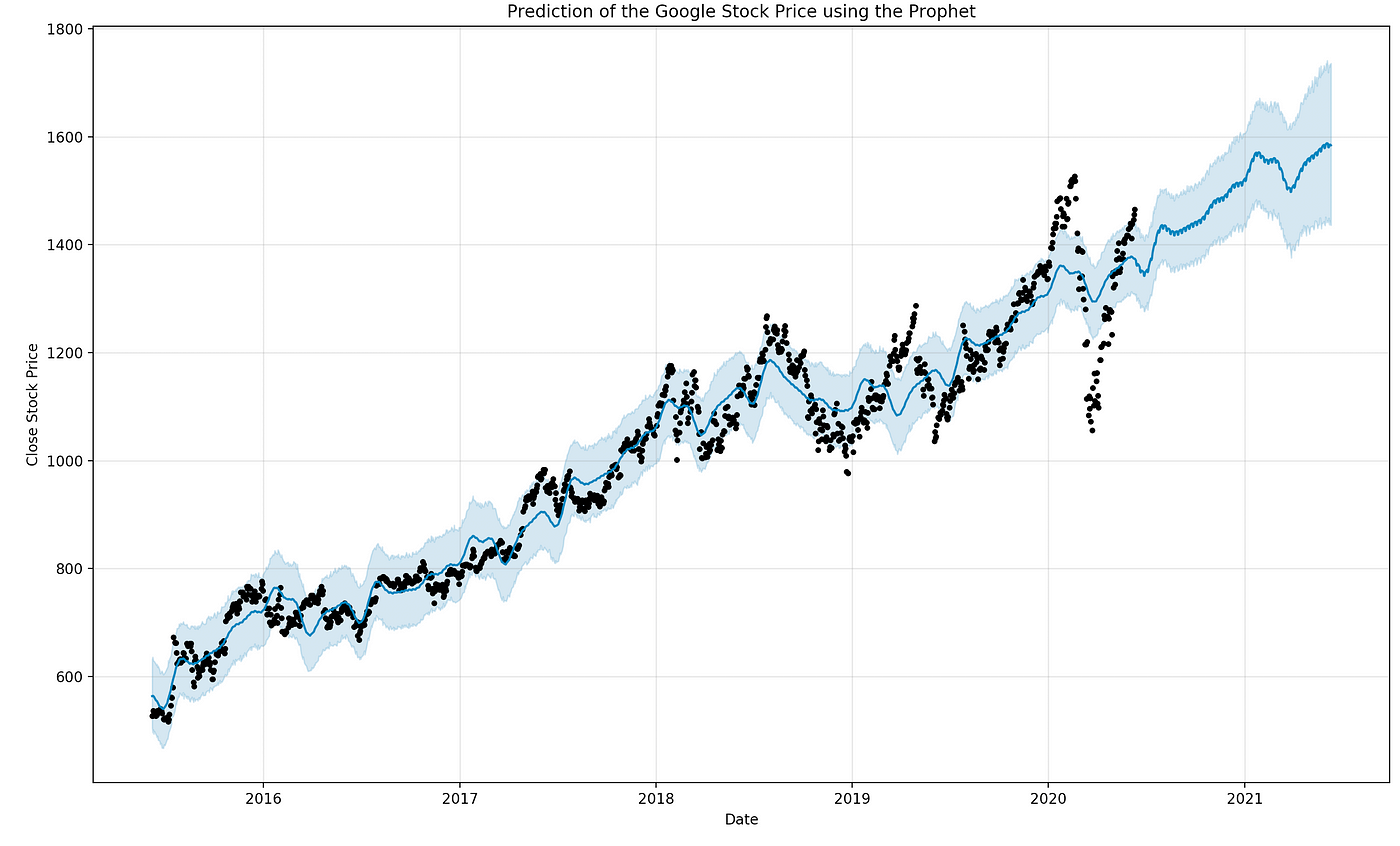
Deep Learning
Anwendungen
-
Zeitreihenanalyse: Markt- & Wetterprognosen, Anomalieerkennung

Deep Learning
Anwendungen
-
Computer Vision: Klassifizierung, Objekterkennung, Bildgenerierung
-
Natural Language Processing: Übersetzungen, Chatbots
-
Reinforcement Learning: Gaming, Robotik, Automatisierung
-
Zeitreihenanalyse: Markt- & Wetterprognosen, Anomalieerkennung
-
Explainable AI: Transparenz, Vertrauen, Sicherheit
Deep Learning
Anwendungen
-
Explainable AI: Transparenz, Vertrauen, Sicherheit

Deep Learning
Anwendungen
-
Computer Vision: Klassifizierung, Objekterkennung, Bildgenerierung
-
Natural Language Processing: Übersetzungen, Chatbots
-
Reinforcement Learning: Gaming, Robotik, Automatisierung
-
Zeitreihenanalyse: Markt- & Wetterprognosen, Anomalieerkennung
-
Explainable AI: Transparenz, Vertrauen, Sicherheit
Deep Learning
Good Practice
-
Daten Erkunden
-
Modell & Trainingsloop erstellen
-
Evaluieren
-
Overfitten
-
Regularisieren
-
Optimieren
Case Study: Fragestellung
- Forschungsfragen
- Ziele
- Anwendungsdomäne
- Daten
Report
- Diskussion
- Konklusion
Auch hilfreich: Lones: How to avoid machine learning pitfalls
Daten Erkunden
- Verstehen: Inhalt, Format, Label, Metadaten
- Visualisieren: Verteilung, Korrelation, Ausreisser
- Preprocessing: normalisieren, skalieren, enkodieren, balancieren
Daten Erkunden
Hands-On: MNIST Datensatz
Öffnen sie dieses Notebook und bearbeiten Sie die Aufgaben. Beantworten Sie so folgende Fragen:
- Welche Daten enthält der Datensatz?
- Welches Format haben die Daten?
- Welche Klassen gibt es und wie sind diese verteilt?
- Wie machen wir die Klassen dem Modell verständlich?
- Welche Skalierung der Daten ist sinnvoll?
Die Lösung finden Sie in diesem Notebook
Notebook auf Drive kopieren um Resultate zu speichern
Daten Erkunden
Hands-On: MNIST Datensatz
Welche Daten enthält der Datensatz?
data.shape -> (N_data, size_input)Die shape eines Datensatzes zeigt die Anzahl der Elemente (N_data) sowie das format der einzelnen Elemente (size_input)
Daten Erkunden
Hands-On: MNIST Datensatz
Welches Format haben die Daten?
Die type(x) Funktion gibt die Klasse von x an
type(data[0]) -> classDie built-in Funktion x.dtype gibt den Datentyp von x an
data.dtype -> data_typeDaten Erkunden
Hands-On: MNIST Datensatz
Welche Klassen gibt es und wie sind diese verteilt?
numpy.unique(x) liefert eine liste aller Elemente die in x vorkommen
labels = np.unique(target)numpy.bincount(x) liefert die Anzahl von Integerwerten in x, geordnet nach Zahlenwert der Integer
counts = np.bincount(target.astype(int))Daten Erkunden
Hands-On: MNIST Datensatz
Wie machen wir die Klassen dem Modell verständlich?
Um Stringlabel in für das Modell verständliche Floats zu verwandeln nutzen wir One-Hot-Encoding
# zB "3" -> [0,0,0,1,0,0,0,0,0,0]
#
from sklearn.preprocessing import OneHotEncoder
encoder = OneHotEncoder()
labels = encoder.fit_transform(target)Achtung: Die letzte Zeile erwartet hier target mit shape (N,1)
Daten Erkunden
Hands-On: MNIST Datensatz
Welche Skalierung der Daten ist sinnvoll?
In den Knoten eines Neuronalen Netzes werden viele Werte aufsummiert, was zu sehr grossen Ergebnissen führen kann.
Ausserdem haben grundsätzilch hohe Features ein stärkeres Gewicht.
Um das zu verhindern werden die Input-Daten auf [-1,1] skaliert.
Dazu benutzt man idR das Min-Max scaling
scaled_data = (data - np.min(data)) / (np.max(data) - np.min(data)) * 2 - 1
Deep Learning

Supervised

Lernen mit Zieldaten (Label / Target)
- Target fuer jeden Datensatz
- Training durch vergleich Output = Target
- Klassifizierung, Spracherkennung
Unsupervised
Lernen ohne Zieldaten
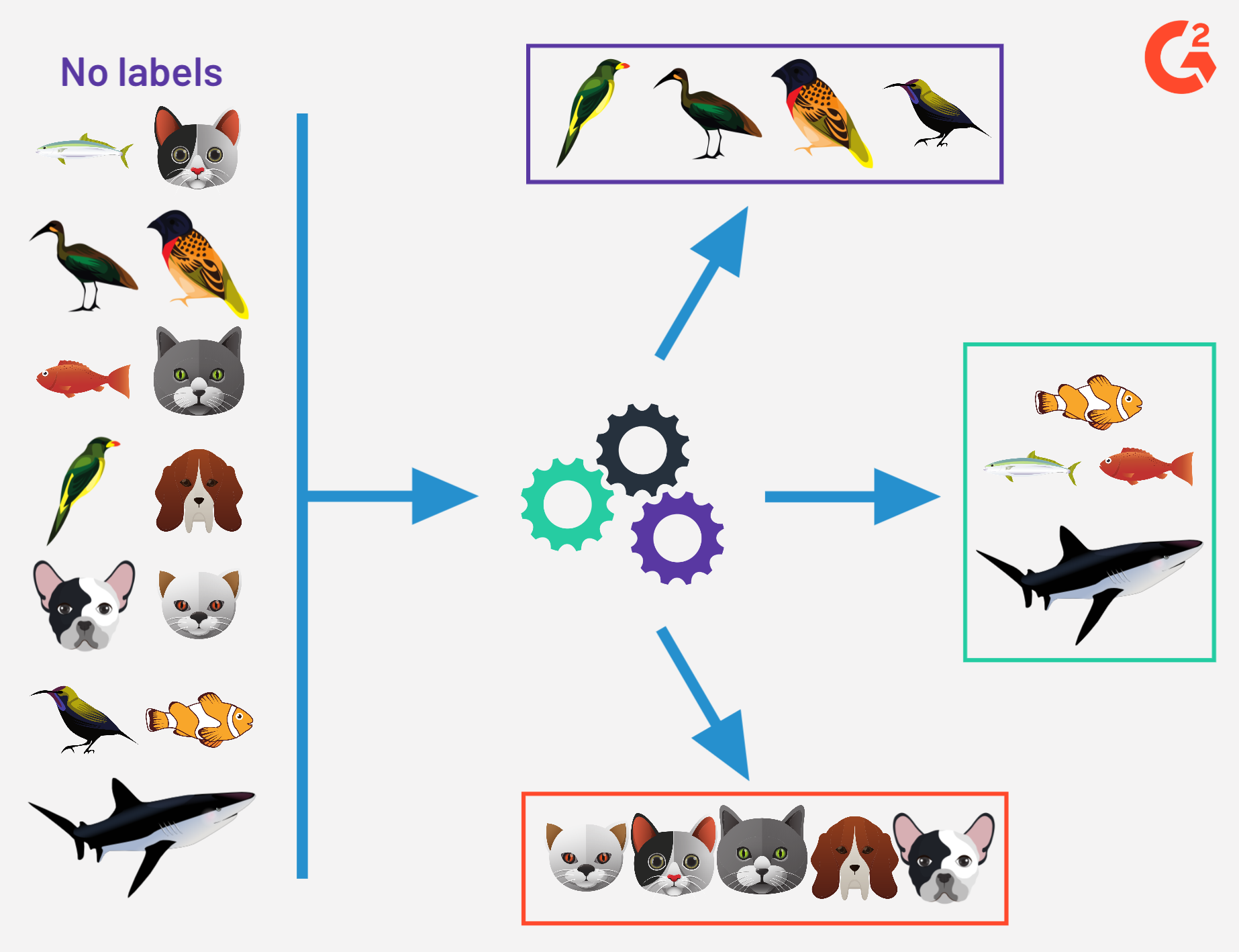
- Kein Target pro Datensatz
- Muster & Strukturen erkennen
- Clustering, Dimensionsreduktion
Reinforcement
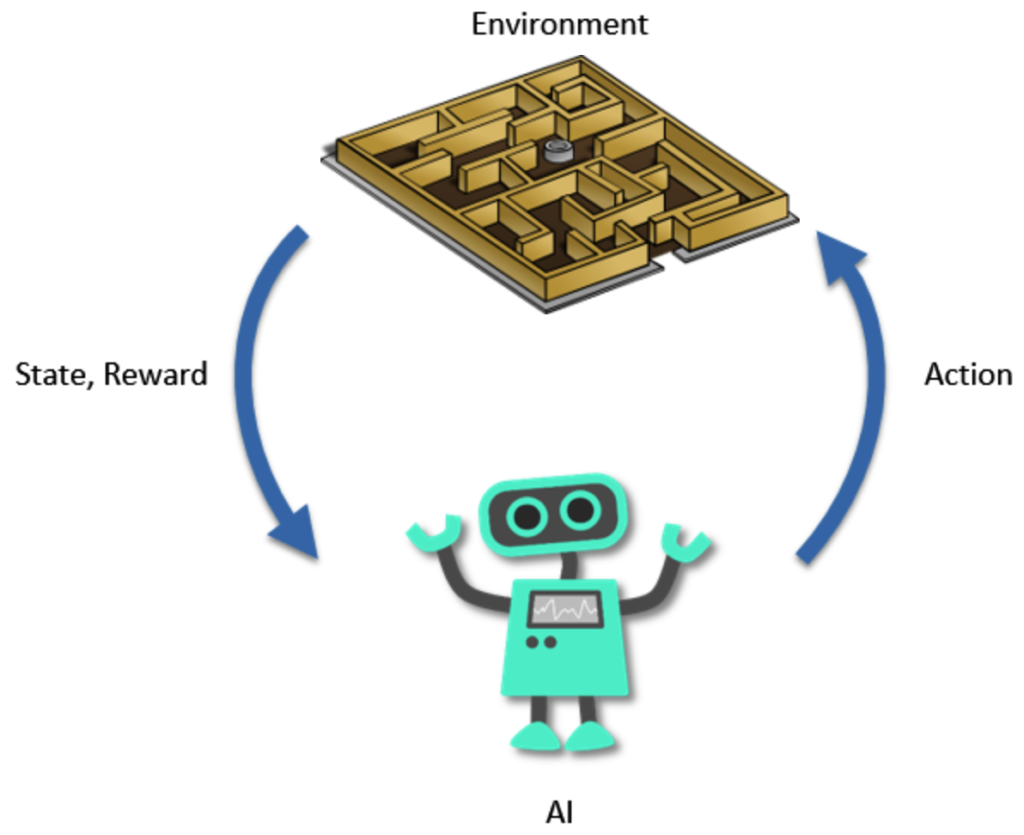
Interaktion mit Umgebung
- Lernen durch Interaktion
- Belohnung & Bestrafung
- Spiele, Roboter, Autonome Systeme
Deep Learning Modell
Architektur: Neuronale Netzstruktur
Neuronales Netz = einfache Dartstellung sehr komplizierter Rechnung
LinReg mit Basisfunktionen aus LinReg mit Basis aus Linreg mit Basis aus ...
Modell = Architektur mit Satz von Parametern

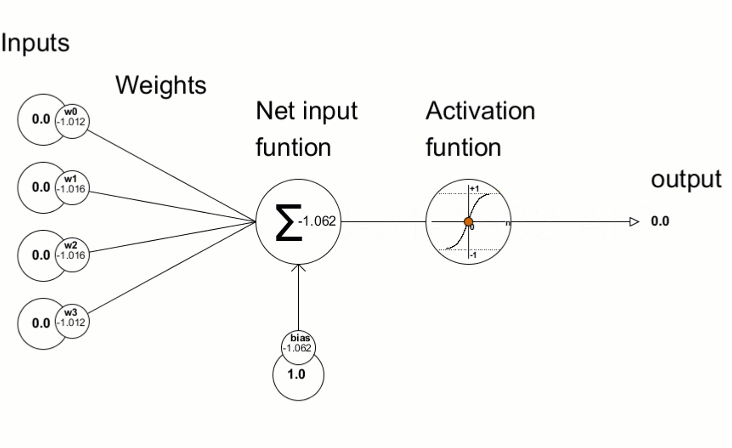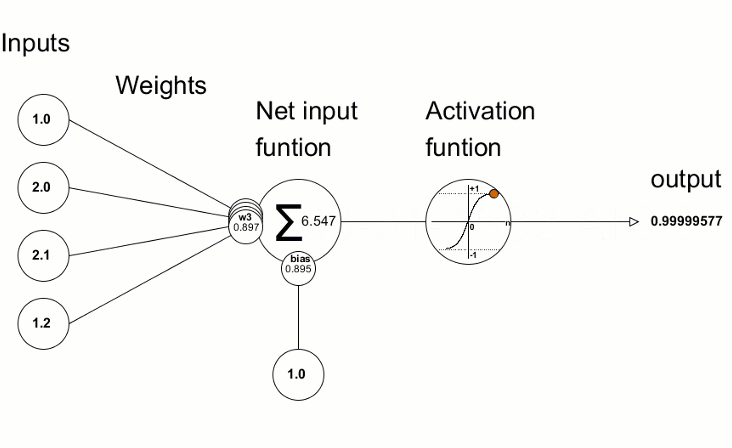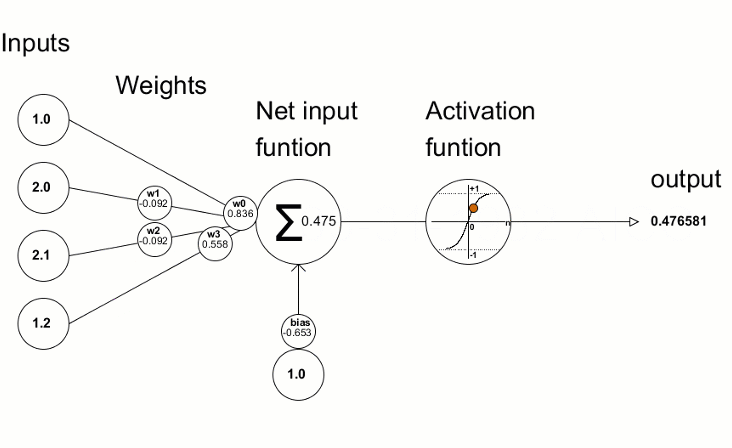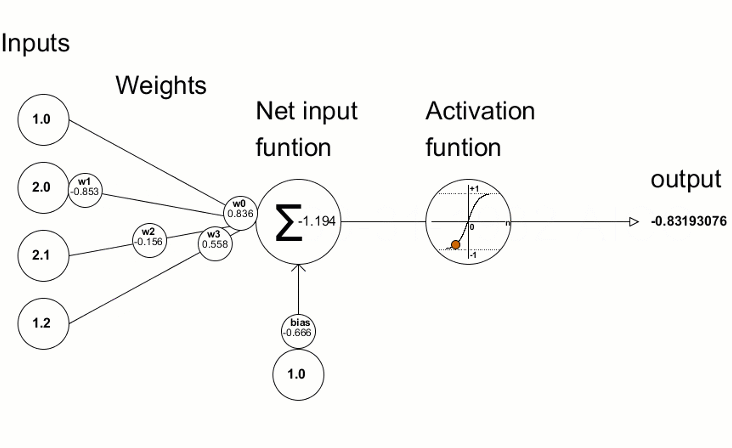
Layer
Layer = Level für Lineare Regression
Mehrere Knoten (Perceptronen)
Knoten = gewichtete Summe & Aktivierungsfunktion

Aktivierungsfunktion
Wofür Aktivierung?
Ohne Aktivierung: N Layer = 1 Layer
Lineare Kombination
von Linearkombinationen
ist eine Linearkombination
Nicht-Lineare Aktivierung
ermöglicht komplexe Modellierung
Aktivierungsfunktion
Wahl der Aktivierung:
- Output: Wertebereich Target
- Hidden: Effizienz (?)
Aktivierungsfunktion
Wahl der Aktivierung:
- Output: Wertebereich Target
- Hidden: Effizienz (ReLU)
Aktivierungsfunktion
Dying ReLU:
- Permanent x < 0
- ReLU & Ableitung = 0
- Perceptron lernt nicht
- Wird Unbrauchbar
Aktivierungsfunktion
Dying ReLU:
- Permanent x < 0
- ReLU & Ableitung = 0
- Perceptron lernt nicht
- Wird Unbrauchbar
PReLU, RReLU, ELU, SELU, GELU, Swish, Mish, ReLU6, ...
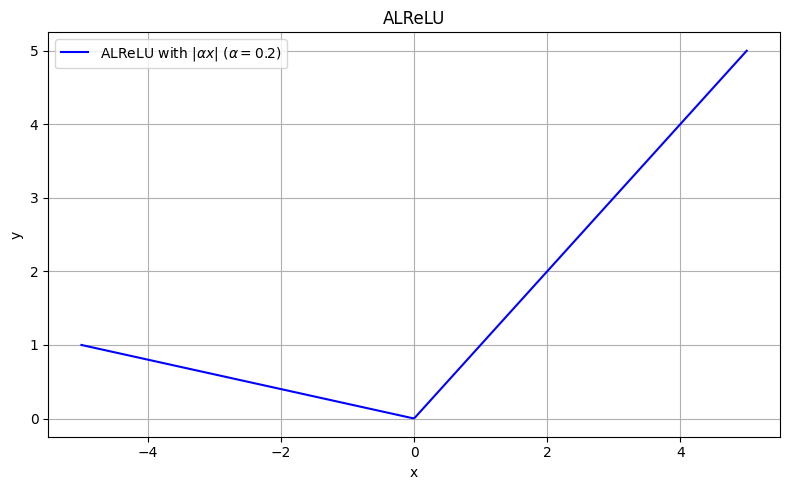
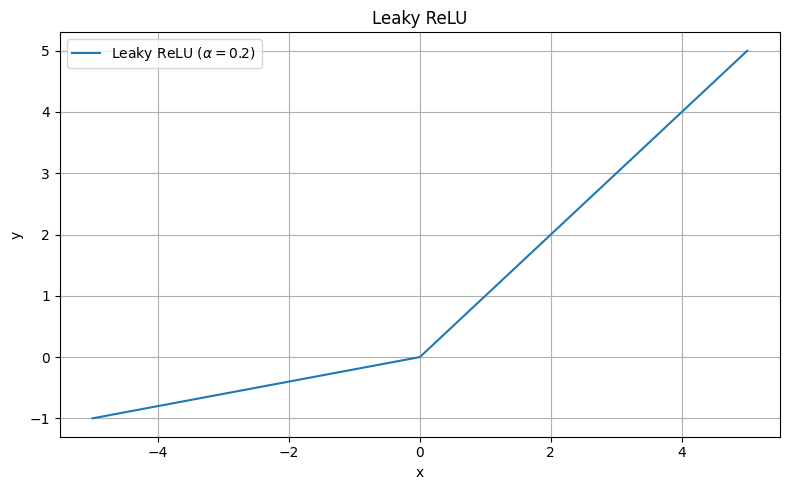
nützlich bei sehr seltener Aktivierung
Aktivierungsfunktion
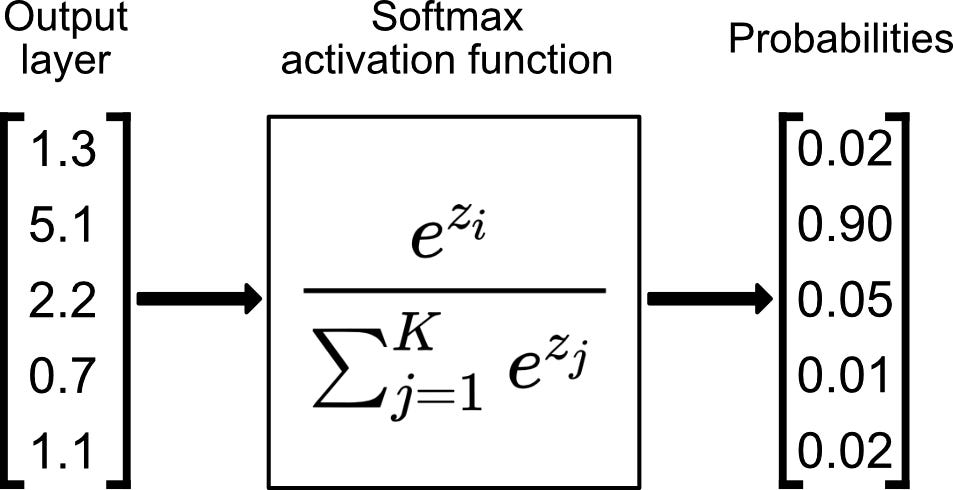
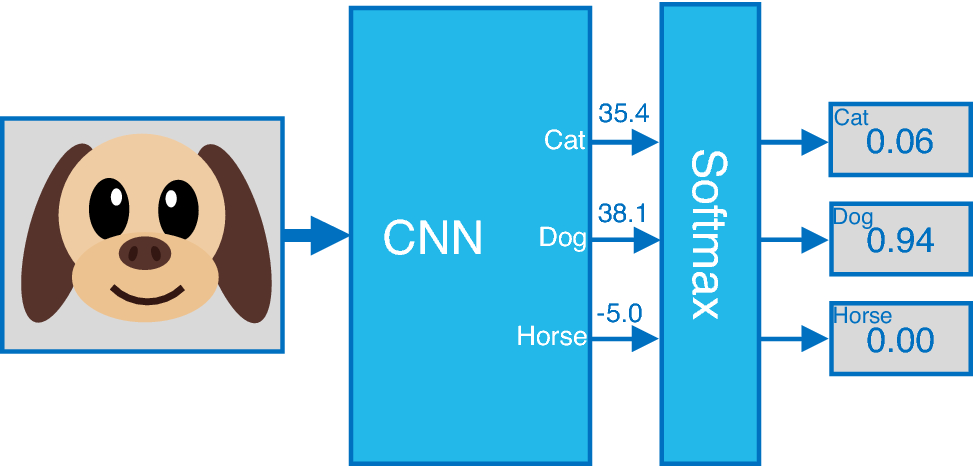
Implementation
| Pytorch | Tensorflow | |
|---|---|---|
| Eigenschaften | Pythonic, einfache Syntax schnelleres Training dynamischer Berenchnungsgraph höhere Flexibilität |
Skalierbar Speichereffizient statisch oder dynamisch |
| Hauptanwendung | Forschung Prototyping |
Grossprojekte Produktion |
| Community | Forschung | Industrie |
| Pakete | TorchText, TorchVision, TorchAudio | TF Extended, TF Lite, TF Serving |


Beide Frameworks sehr nützlich & weit verbreitet
Mathematik identisch & Aufbau sehr ähnlich
Wahl meist durch Arbeitsumfeld bestimmt
Architektur entwerfen
- Aufgabe klar definieren (Klassifikation, Regression, Erkennung, ...)
- Ein- und Ausgabedimension festlegen (MNIST: In: 784; Out: 10)
- Geeignete Art von Schichten bestimmen (Linear, Convolutional, ...)
- Anzahl Schichten und Neuronen pro Schicht festlegen
- Aktivierungsfunktionen festlegen (Hidden & Output)
Wenn möglich, bereits existierende Architektur / Modelle verwenden
Implementation
- MNIST Classifier
Implementation
from torch import nn
import torch.nn.functional as F
class Classifier(nn.Module):
def __init__(self):
super().__init__()
def forward(self, x):
return x
model = Classifier()
output = model(data)
Pytorch (Meta)
- MNIST Classifier
Implementation
from torch import nn
import torch.nn.functional as F
class Classifier(nn.Module):
def __init__(self):
super().__init__()
self.fc4 = nn.Linear(784, 10)
def forward(self, x):
x = self.fc4(x)
return x
model = Classifier()
output = model(data)
Pytorch (Meta)
- MNIST Classifier
- 10 Outputs
Implementation
from torch import nn
import torch.nn.functional as F
class Classifier(nn.Module):
def __init__(self):
super().__init__()
self.fc1 = nn.Linear(784, 64)
self.fc2 = nn.Linear(64, 64)
self.fc3 = nn.Linear(64, 64)
self.fc4 = nn.Linear(64, 10)
def forward(self, x):
x = self.fc1(x)
x = self.fc2(x)
x = self.fc3(x)
x = self.fc4(x)
return x
model = Classifier()
output = model(data)
Pytorch (Meta)
- MNIST Classifier
- 10 Outputs
- 3 Hidden Layer
Implementation
from torch import nn
import torch.nn.functional as F
class Classifier(nn.Module):
def __init__(self):
super().__init__()
self.fc1 = nn.Linear(784, 64)
self.fc2 = nn.Linear(64, 64)
self.fc3 = nn.Linear(64, 64)
self.fc4 = nn.Linear(64, 10)
def forward(self, x):
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
x = F.relu(self.fc3(x))
x = self.fc4(x)
return x
model = Classifier()
output = model(data)
Pytorch (Meta)
- MNIST Classifier
- 10 Outputs
- 3 Hidden Layer
Implementation
from torch import nn
import torch.nn.functional as F
class Classifier(nn.Module):
def __init__(self):
super().__init__()
self.fc1 = nn.Linear(784, 64)
self.fc2 = nn.Linear(64, 64)
self.fc3 = nn.Linear(64, 64)
self.fc4 = nn.Linear(64, 10)
def forward(self, x):
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
x = F.relu(self.fc3(x))
x = F.softmax(self.fc4(x), dim=1)
return x
model = Classifier()
output = model(data)
Pytorch (Meta)
- MNIST Classifier
- 10 Outputs
- 3 Hidden Layer
- Softmax activation
Implementation
from torch import nn
import torch.nn.functional as F
class Classifier(nn.Module):
def __init__(self):
super().__init__()
self.fc1 = nn.Linear(784, 64)
self.fc2 = nn.Linear(64, 64)
self.fc3 = nn.Linear(64, 64)
self.fc4 = nn.Linear(64, 10)
def forward(self, x):
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
x = F.relu(self.fc3(x))
x = F.softmax(self.fc4(x), dim=1)
return x
model = Classifier()
output = model(data)
Pytorch (Meta)
import tensorflow as tf
from tensorflow.keras import layers
class Classifier(tf.keras.Model):
def __init__(self):
super(Classifier, self).__init__()
self.fc1 = layers.Dense(64, activation='relu')
self.fc2 = layers.Dense(64, activation='relu')
self.fc3 = layers.Dense(64, activation='relu')
self.fc4 = layers.Dense(10, activation='softmax')
def call(self, x):
x = self.fc1(x)
x = self.fc2(x)
x = self.fc3(x)
x = self.fc4(x)
return x
model = Classifier()
model.build((None, 784))
model(data)
Tensorflow (Google)
- MNIST Classifier
- 10 Outputs
- 3 Hidden Layer
- Softmax activation
Implementation
import torch.nn as nn
model = nn.Sequential(
nn.Linear(784, 64),
nn.ReLU(),
nn.Linear(64, 64),
nn.ReLU(),
nn.Linear(64, 64),
nn.ReLU(),
nn.Linear(64, 10),
nn.Softmax(dim=1)
)
output = model(data)Pytorch (Meta)
from tensorflow.keras import models
model = models.Sequential([
layers.Dense(64, activation='relu', input_shape=(784,)),
layers.Dense(64, activation='relu'),
layers.Dense(64, activation='relu'),
layers.Dense(10, activation='softmax')
])
model(data)
Tensorflow (Google)
- MNIST Classifier
- 10 Outputs
- 3 Hidden Layer
- Softmax activation
Trainingsloop
- Daten laden (batch)
- Modell anwenden (forward)
- Loss berechnen
- Updates berechnen (backward)
- Update durchfüren
for images, labels in trainloader: prediction = model(images) loss = criterion(prediction, labels) optimizer.zero_grad()
loss.backward() optimizer.step()trainloader = DataLoader(trainset, batch_size=256, shuffle=True)Trainingsloop entwerfen
- Aufgabe klar definieren
- Lossfunktion bestimmen
- Berechnungsschritte definieren
Loss Funktion
- Definiert das Ziel des Trainings
- Ziel: Loss minimieren
- erlaubt Vergleich von Modellen
- verschiedene Losses für verschiedene Aufgaben
Loss Funktion
- Mean Squared Error (MSE):
mittlerer quadratische Abweichung
- Binäre Cross-Entropy (BCE):
vergleich von Wahrscheinlichkeit einer Klasse
- Cross-Entropy (CE):
vergleich von Wahrscheinlichkeiten mehrerer Klassen
Implementation
- Loss: CrossEntropy
Implementation
criterion = nn.CrossEntropyLoss()
Pytorch
- Loss: CrossEntropy
Implementation
criterion = nn.CrossEntropyLoss()
optimizer = optim.Adam(model.parameters(), lr=0.003)
Pytorch
- Loss: CrossEntropy
- Optimizer: Adam
Implementation
criterion = nn.CrossEntropyLoss()
optimizer = optim.Adam(model.parameters(), lr=0.003)
for e in range(epochs):
Pytorch
- Loss: CrossEntropy
- Optimizer: Adam
Implementation
criterion = nn.CrossEntropyLoss()
optimizer = optim.Adam(model.parameters(), lr=0.003)
for e in range(epochs):
for images, labels in trainloader:
Pytorch
- Loss: CrossEntropy
- Optimizer: Adam
Implementation
criterion = nn.CrossEntropyLoss()
optimizer = optim.Adam(model.parameters(), lr=0.003)
for e in range(epochs):
for images, labels in trainloader:
prediction = model(images)
loss = criterion(prediction, labels)
Pytorch
- Loss: CrossEntropy
- Optimizer: Adam
Forward-Pass
Implementation
criterion = nn.CrossEntropyLoss()
optimizer = optim.Adam(model.parameters(), lr=0.003)
for e in range(epochs):
for images, labels in trainloader:
prediction = model(images)
loss = criterion(prediction, labels)
optimizer.zero_grad()
loss.backward()
optimizer.step()
Pytorch
- Loss: CrossEntropy
- Optimizer: Adam
Backward-Pass
Implementation
criterion = nn.CrossEntropyLoss()
optimizer = optim.Adam(model.parameters(), lr=0.003)
for e in range(epochs):
running_loss = 0
for images, labels in trainloader:
prediction = model(images)
loss = criterion(prediction, labels)
optimizer.zero_grad()
loss.backward()
optimizer.step()
running_loss += loss.item()Pytorch
- Loss: CrossEntropy
- Optimizer: Adam
Implementation
criterion = nn.CrossEntropyLoss()
optimizer = optim.Adam(model.parameters(), lr=0.003)
for e in range(epochs):
running_loss = 0
for images, labels in trainloader:
prediction = model(images)
loss = criterion(prediction, labels)
optimizer.zero_grad()
loss.backward()
optimizer.step()
running_loss += loss.item()Pytorch
- Loss: CrossEntropy
- Optimizer: Adam
model.compile(optimizer=optimizers.Adam(learning_rate=0.003),
loss='sparse_categorical_crossentropy',
metrics=['accuracy'])
history = model.fit(train_images, train_labels, epochs=1, batch_size=64)
print(f'Training loss: {history.history["loss"][0]}')
Tensorflow
Update
Ableitung der Kosten -> Richtung für Verbesserung -> Update
Gradient Descent
Lernrate
Update

Ableitung der Kosten -> Richtung für Verbesserung -> Update
Gradient Descent
Update

Ableitung der Kosten -> Richtung für Verbesserung -> Update
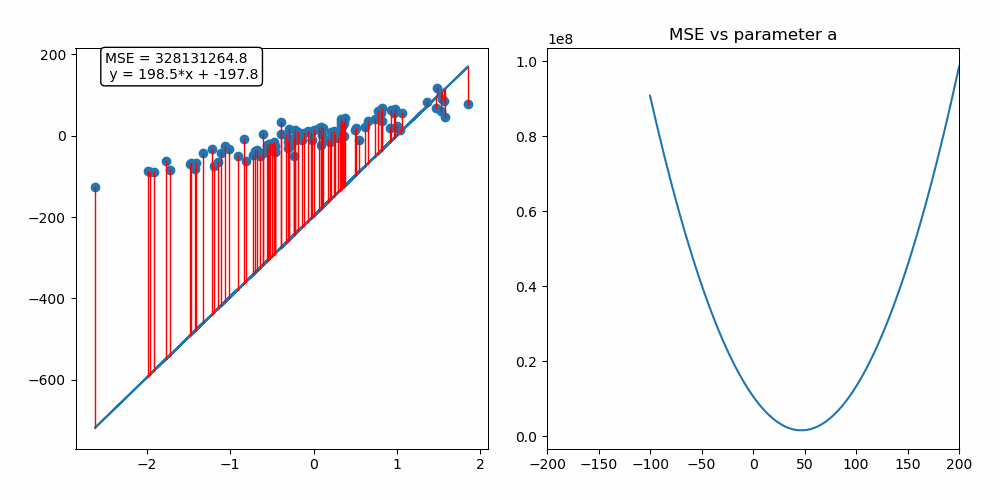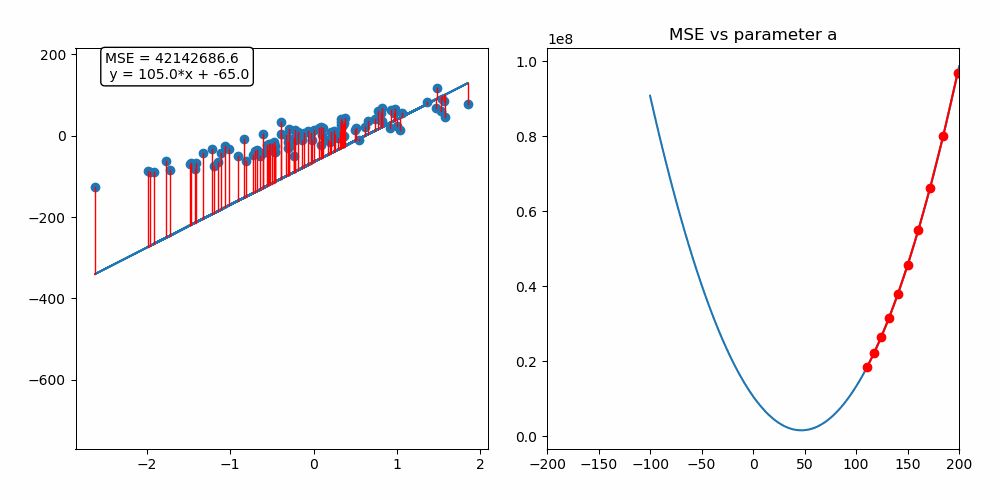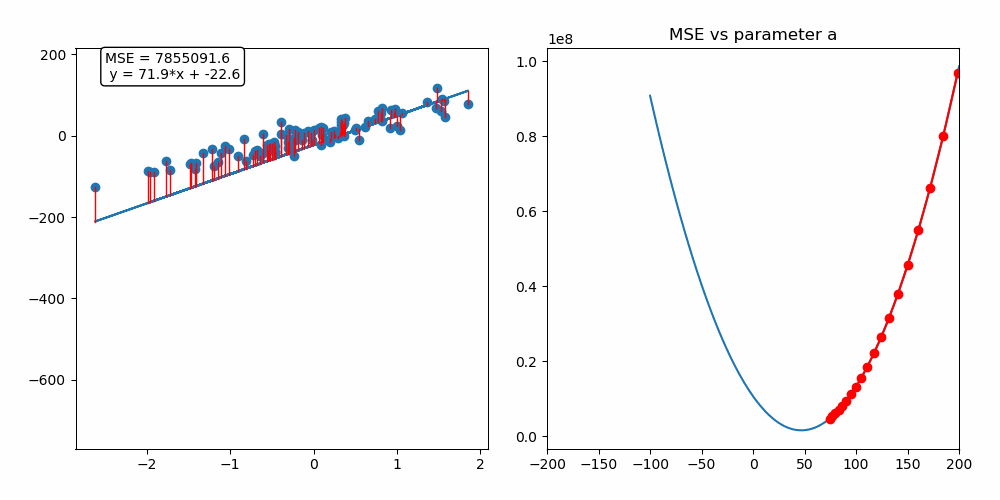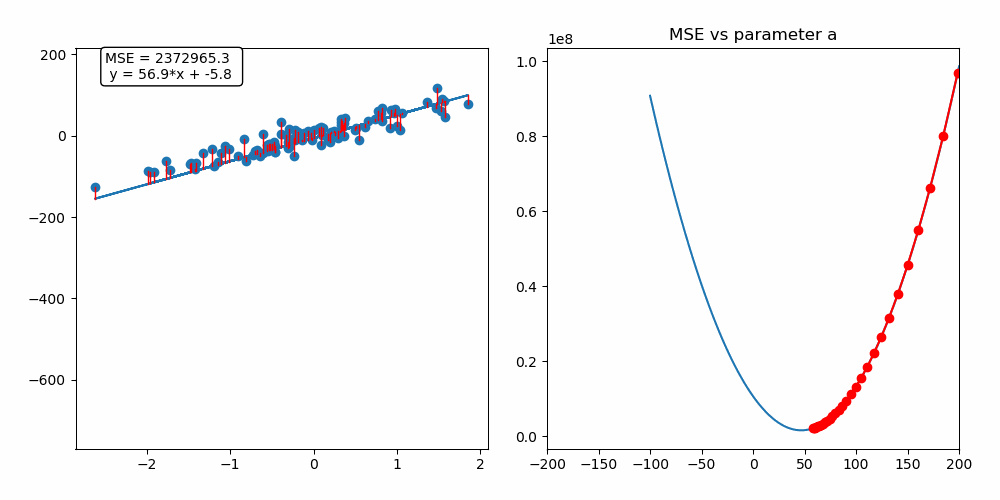
Gradient Descent
Update

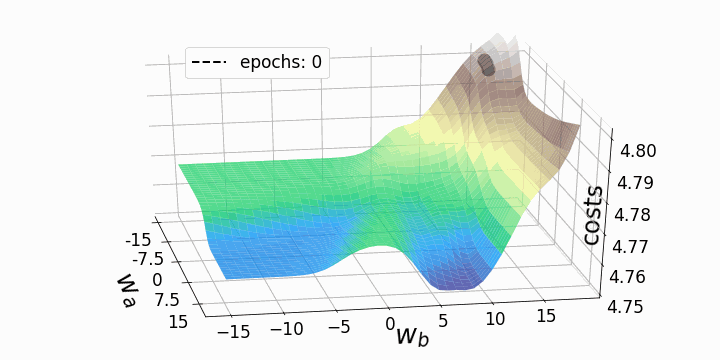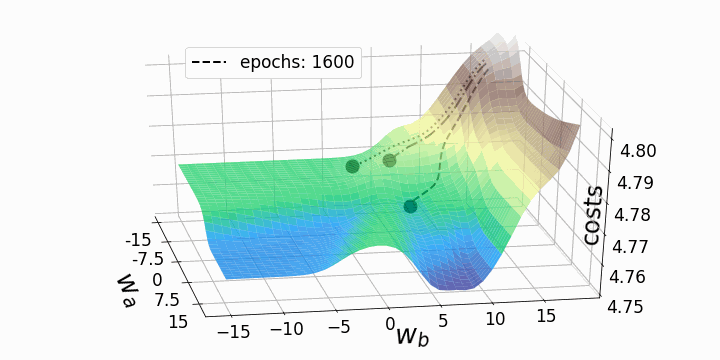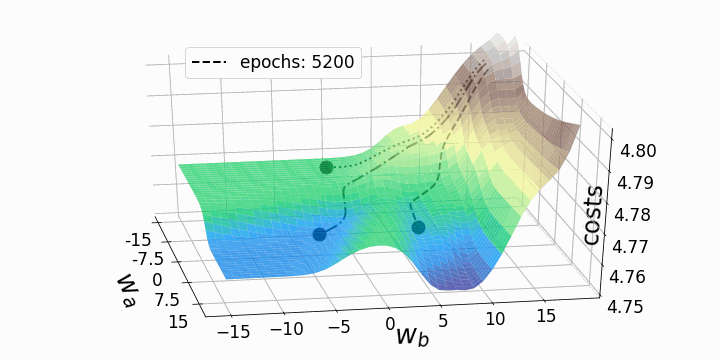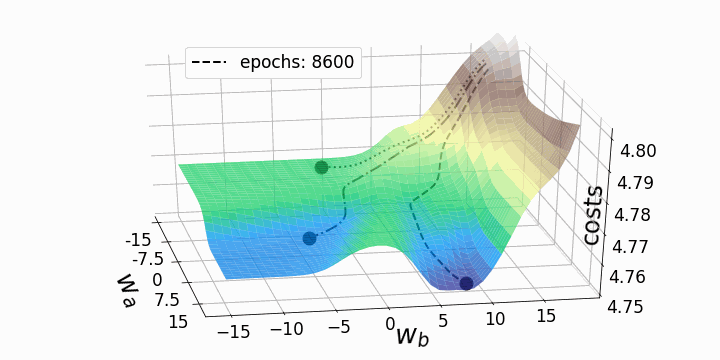
Ableitung der Kosten -> Richtung für Verbesserung -> Update
Gradient Descent
Optimizer


Gradient Descent
Optimizer


Gradient Descent
Optimizer


Gradient Descent
Optimizer


Gradient Descent
Optimizer


Gradient Descent
Optimizer


Gradient Descent
Optimizer


Gradient Descent
Optimizer


Gradient Descent
Optimizer


Gradient Descent
Optimizer
Berechnet Ableitung
für jedes Update
mit gesamten Datensatz
folgt exakt steilstem Abstieg
Bei Millionen von Daten
sehr rechenintensiv...
Gradient Descent
Optimizer
Gradient Descent
Berechnet Ableitung
für jedes Update
mit gesamten Datensatz
folgt exakt steilstem Abstieg
Bei Millionen von Daten
sehr rechenintensiv...
Stochastic Gradient Descent (SGD)
Zerlegt Datensatz in Batches
Update nach jeder Batch
folgt Schätzung des steilsten Abstiegs
Forschritt kann Schwanken
Schnelle Konvergenz
dank schneller Rechnung
Optimizer

Gradient Descent
Optimizer
SGD

Momentum
Model & Trainingsloop
Hands-On: MNIST Classifier
Bearbeiten Sie dieses Notebook
- Erstellen Sie einen MNIST Classifier
- Definieren Sie die Trainingsloop
- Testen sie die Trainingsloop ueber zwei Epochen
Die Lösung finden Sie in diesem Notebook
Evaluieren
Wie gut und stabil ist mein Model?
- Performance Messen
- Test auf unbekannten Daten
- Robust gegen Änderungen
- Vergleich mit Mensch?
Performance Messen
- Kosten vs Accuracy
- Kosten: Training, nicht interpretierbar
- Accuracy: verständliches Mass der Leistung

Performance Messen
- Kosten vs Accuracy
- Kosten: Training, nicht interpretierbar
- Accuracy: verständliches Mass der Leistung
- Klassifizierung:
- Accuracy
- Precision & Recall
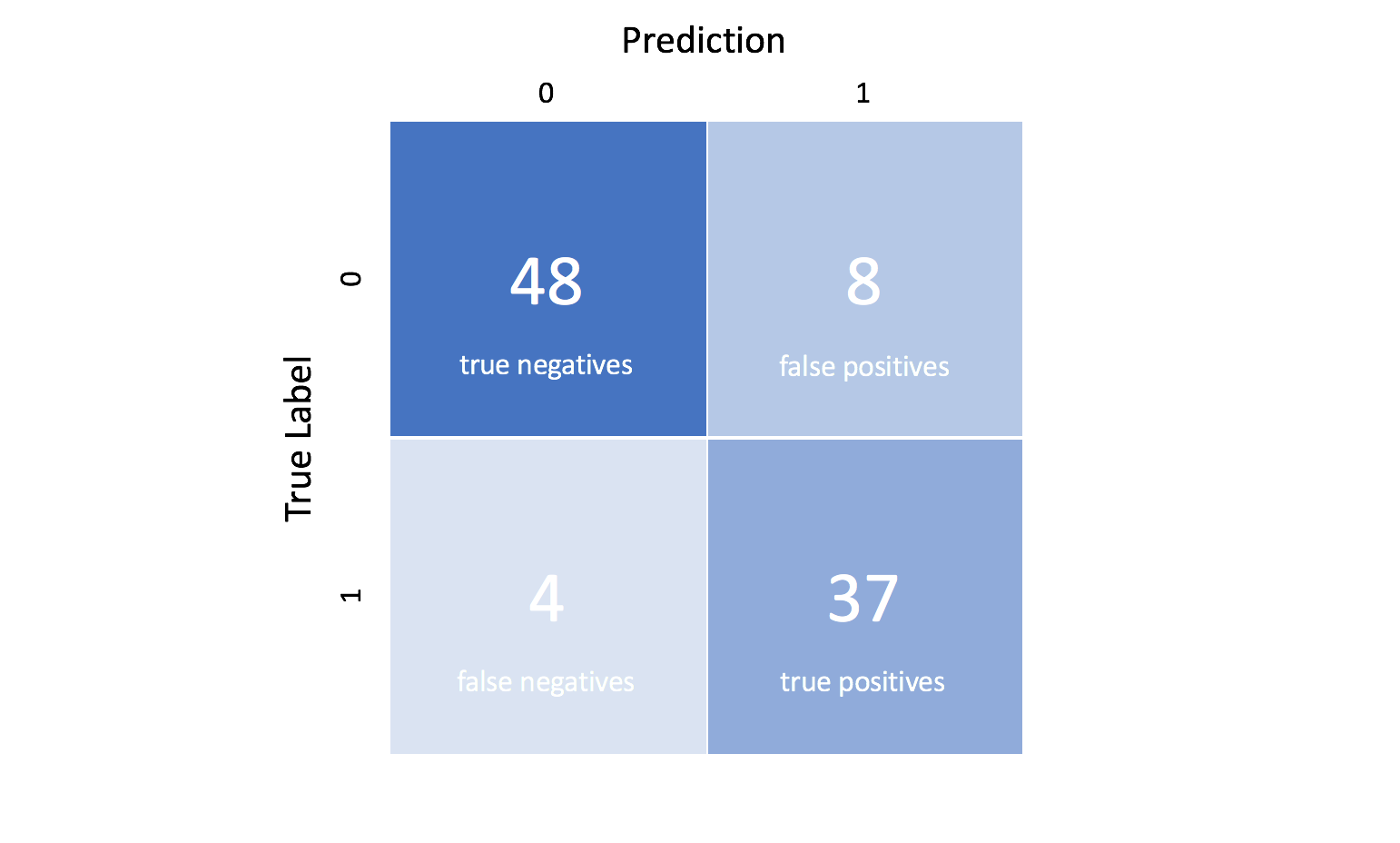
Performance Messen
- Kosten vs Accuracy
- Kosten: Training, nicht interpretierbar
- Accuracy: verständliches Mass der Leistung
- Klassifizierung:
- Accuracy (Binäres label & Balancierte Daten)
- Precision & Recall (Reinheit & Vollständigkeit)
- Confusion Matrix (Interpretation)
- F1 Score (vereint Precision & Recall)
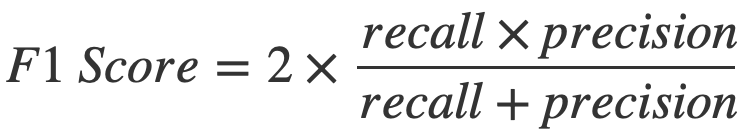

Performance Messen
- Kosten vs Accuracy
- Kosten: Training, nicht interpretierbar
- Accuracy: verständliches Mass der Leistung
- Klassifizierung:
- Accuracy (Binäres label & Balancierte Daten)
- Precision & Recall (Reinheit & Vollständigkeit)
- Confusion Matrix (Interpretation)
- F1 Score (vereint Precision & Recall)
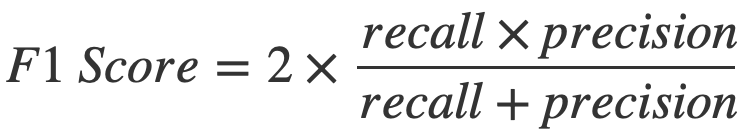
from sklearn.metrics import confusion_matrix, f1_score
conf_mat = confusion_matrix(all_labels, all_preds)
f1 = f1_score(all_labels, all_preds, average='macro')Unbekannte Daten
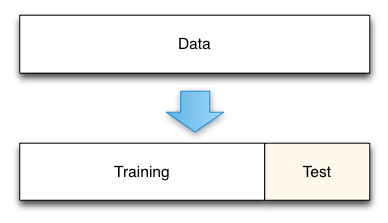
- Train-Test Split
- Training mit Train, Evaluation mit Test
- Verfolge bei Training:
für train & test je loss & accuracy
Robust
- Training an verschiedenen Punkten starten

Robust
- Training an verschiedenen Punkten starten
- k-fold cross-validation (mehr dazu)
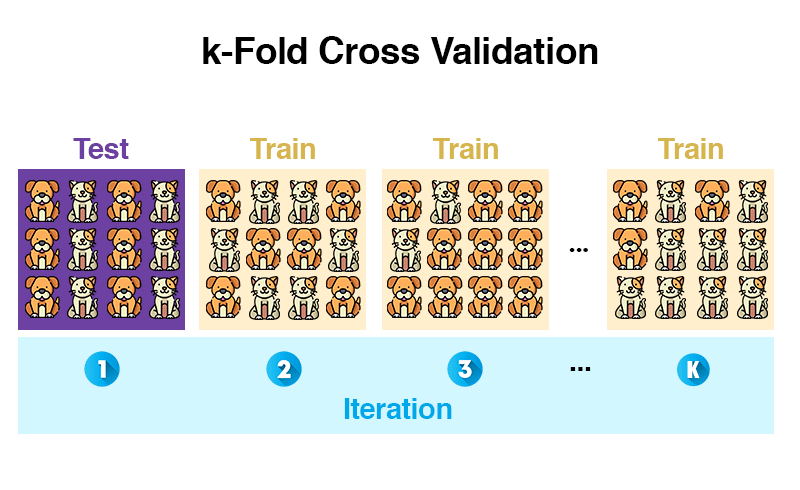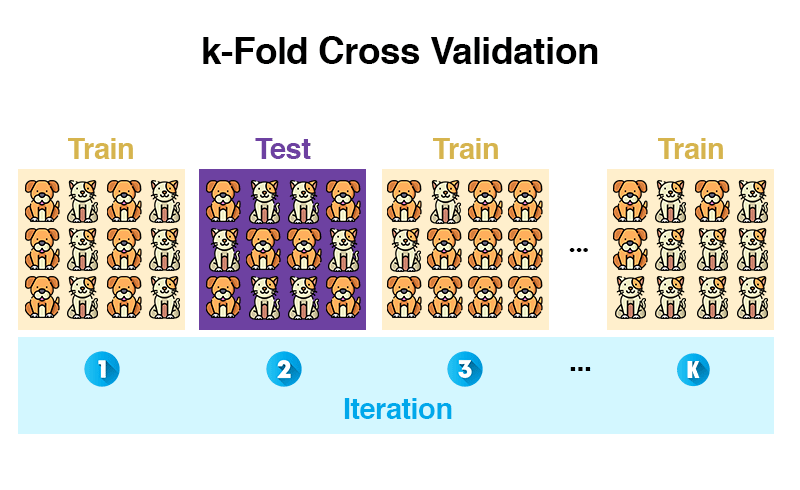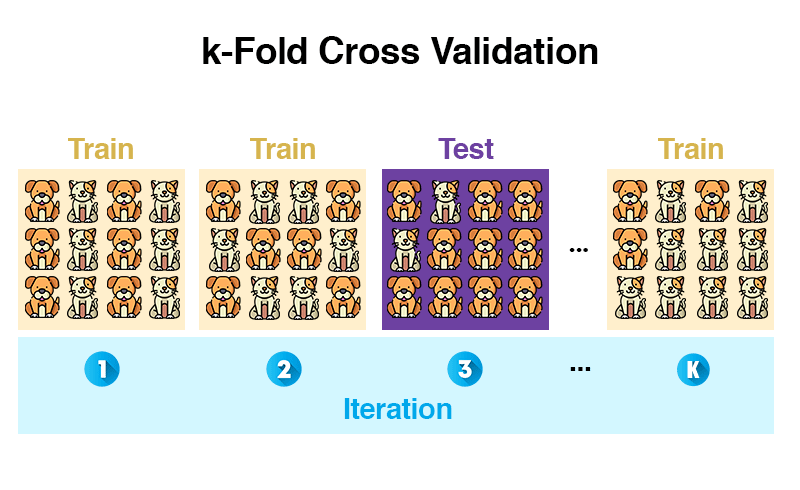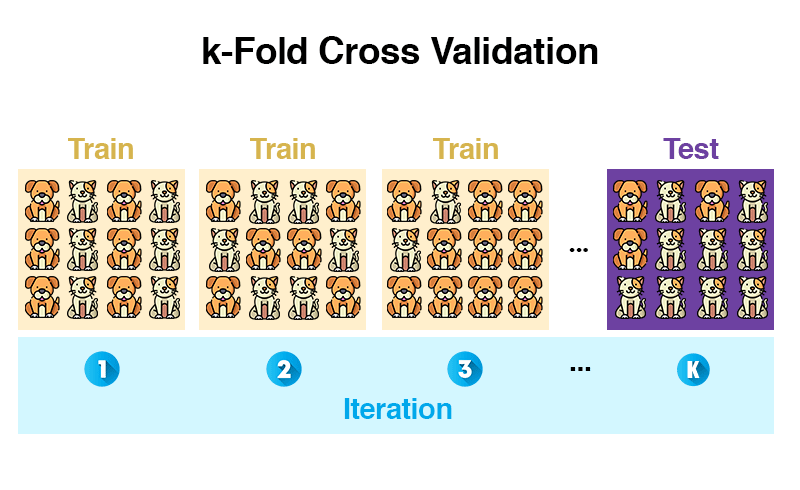
Vergleich mit Mensch
ImageNet Klassifikation

Vergleich mit Mensch
ImageNet Klassifikation

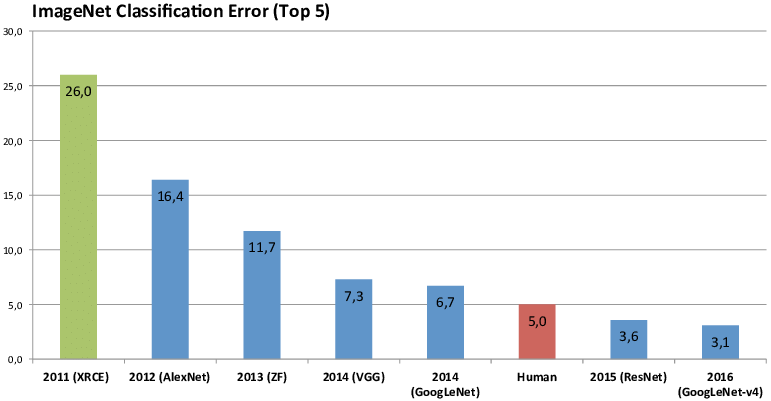
Vergleich mit Mensch
ImageNet Klassifikation


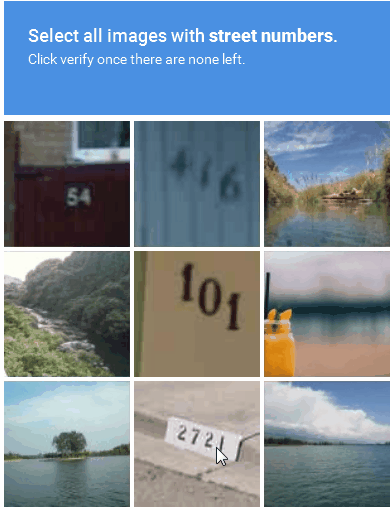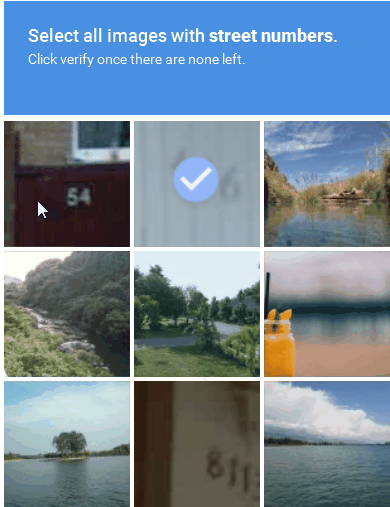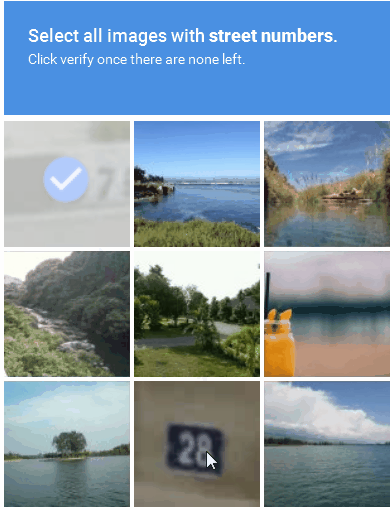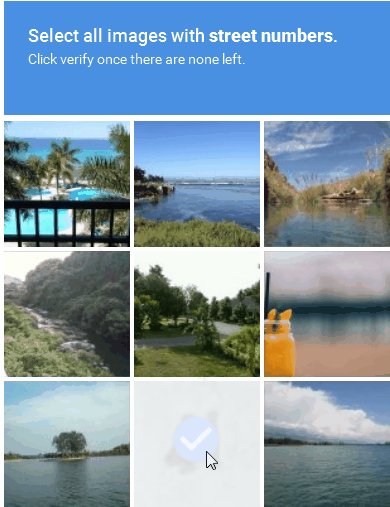
Evaluieren
Hands-On: MNIST Classifier
Bearbeiten Sie dieses Notebook
- Berechnen Sie die Konfusionsmatrix sowie den F1 score
auf einem beliebigen Datensatz
- Berechnen Sie diese explizit für ein untrainiertes Modell
auf dem Testdatensatz
Die Lösung finden Sie in diesem Notebook
Overfitting
- zu stark an Trainingsdaten angepasst
- schlechte verallgemeinerung auf Testdaten
- Model zu komplex / zu lange trainiert
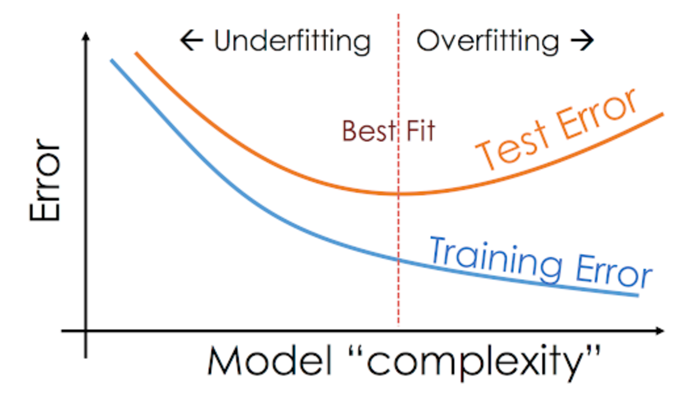
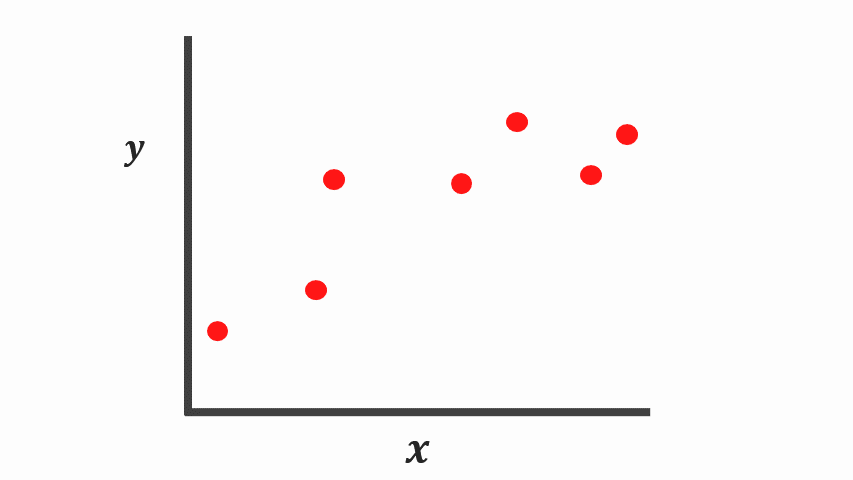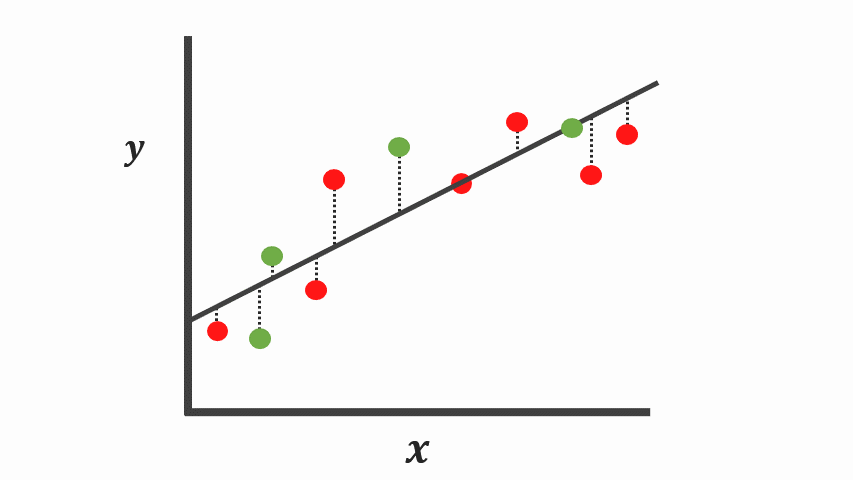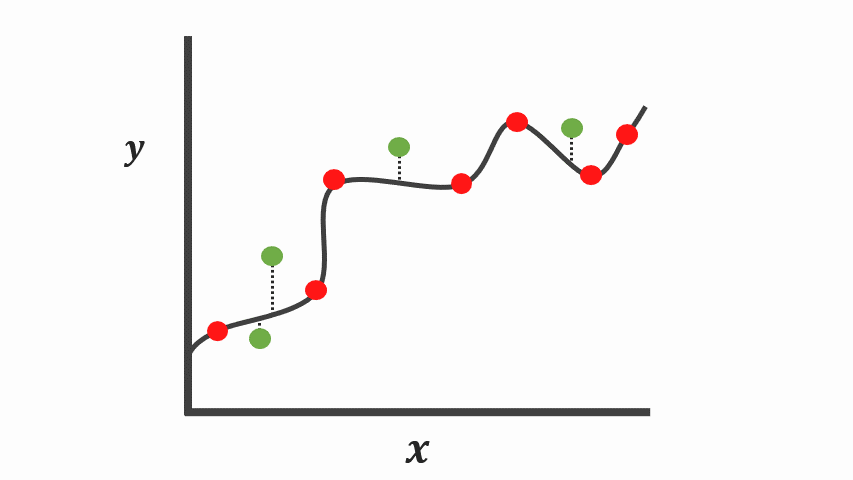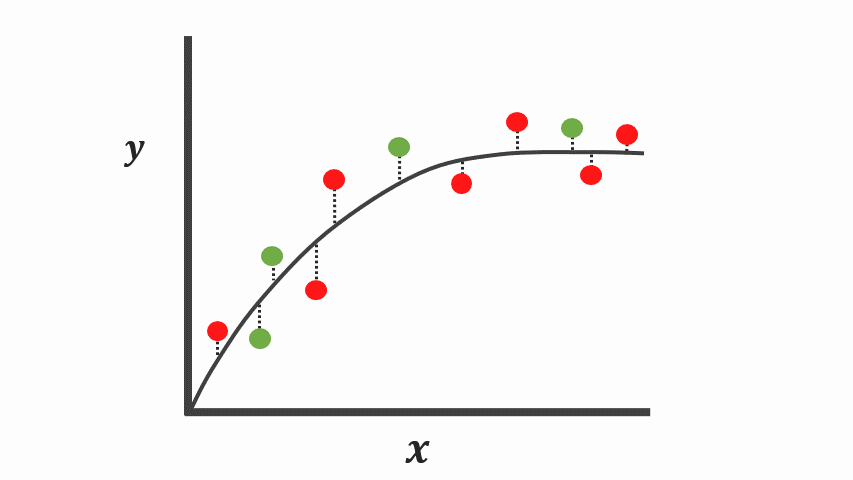
Overfitting
- zu stark an Trainingsdaten angepasst
- schlechte verallgemeinerung auf Testdaten
- Schlecht regularsiert / zu wenig Parameter
Overfitting
- zu stark an Trainingsdaten angepasst
- schlechte verallgemeinerung auf Testdaten
- Schlecht regularsiert / zu wenig Parameter
Gezielt Overfitten
Ist das Modell geeignet, Muster zu erkennen?
- overfitten auf einer batch (sanity check)
- catch bugs fast
# Get one batch from the training_loader
images, labels = next(iter(training_loader))
# alternativ:
for images, labels in training_loader:
break
# Train the model on the batch for 100 iterations
for _ in range(100):
train(model, criterion, optimizer, [(images, labels)])
Gezielt Overfitten
Ist das Modell geeignet, Muster zu erkennen?
- overfitten auf einer batch (sanity check)
- catch bugs fast
- Loss steigt -> hohe learning rate, +/- vertauscht
- Loss explodiert -> hohe lr, numerisches problem
- Loss oszilliert -> hohe lr, data / label fehlerhaft geladen
- Loss plateau -> tiefe lr, backprob error, falscher Input in Loss
Overfitten
Hands-On: MNIST Classifier
Bearbeiten Sie dieses Notebook
- Wählen Sie eine zufällige Batch zum overfitten
- Trainieren Sie auf dieser Batch für 100 Epochen
- Evaluieren Sie das Modell an dieser Batch und den Testdaten
Die Lösung finden Sie in diesem Notebook
Text
Tiefes NN kann jede Funktion fitten
-> overfit leicht
-> Generalisierung schwer
Regularisierung reduziert Varianz,
ohne Bias zu erhöhen
-> Modell lernt "einfach" & robust zu sein
Wieso Regularisieren?
Regularisieren
- reduziert Overfitting
(essentiell bei grossen NN)
- verbessert Generalisierung
- robustere Models & Training
- Balance: Komplexität - Generalisierung
Regularisieren
- L1 (Lasso):
- kleine Parameter
- Gewichte -> 0 => Feature Auswahl
l1_regularization_loss = torch.norm(model.parameters(), 1)Regularisieren
- L1 (Lasso):
- kleine Parameter
- Gewichte -> 0 => Feature Auswahl
- L2 (Ridge):
- kleine, ausgeglichene Parameter
- meistgebrauchte regularisation
l1_regularization_loss = torch.norm(model.parameters(), 1)optimizer = torch.optim.Adam(model.parameters(), lr=lr, weight_decay=beta)
Regularisieren
- L1 (Lasso):
- kleine Parameter
- Gewichte -> 0 => Feature Auswahl
- L2 (Ridge):
- kleine, ausgeglichene Parameter
- meistgebrauchte regularisation
- Dropout: setzt zufällig Neuronen auf 0
- Modell redundant & robust
l1_regularization_loss = torch.norm(model.parameters(), 1)optimizer = torch.optim.Adam(model.parameters(), lr=lr, weight_decay=beta)
nn.Dropout(0.2) # 0.2 of neurons set to 0Regularisieren
- L1 (Lasso):
- kleine Parameter
- Gewichte -> 0 => Feature Auswahl
- L2 (Ridge):
- kleine, ausgeglichene Parameter
- meistgebrauchte regularisation
- Dropout: setzt zufällig Neuronen auf 0
- Modell redundant & robust
- Modell redundant & robust
- Batch Normalization: Normalisiert Layer Input
- Reduziert Abhängikeit von vorigen Layern
l1_regularization_loss = torch.norm(model.parameters(), 1)optimizer = torch.optim.Adam(model.parameters(), lr=lr, weight_decay=beta)
nn.Dropout(0.2) # 0.2 of neurons set to 0nn.BatchNorm1d()PyTorch
Regularisieren
- L1 (Lasso):
- kleine Parameter
- Gewichte -> 0 => Feature Auswahl
- L2 (Ridge):
- kleine, ausgeglichene Parameter
- meistgebrauchte regularisation
- Dropout: setzt zufällig Neuronen auf 0
- Modell redundant & robust
- Modell redundant & robust
- Batch Normalization: Normalisiert Layer Input
- Reduziert Abhängikeit von vorigen Layern
Dense(N, kernel_regularizer=keras.regularizers.l2(beta), bias_regularizer=keras.regularizers.l2(beta))
tf.keras.layers.Dropout(0.2) # 0.2 of neurons set to 0tf.keras.layers.BatchNormalization(),Dense(N, kernel_regularizer=keras.regularizers.l1(beta), bias_regularizer=keras.regularizers.l1(beta))
TensorFlow
Data Augmentation
- Mehr Daten -> grössere Modelle -> komplexere Aufgaben
Data Augmentation
- Mehr Daten -> grössere Modelle -> komplexere Aufgaben
- Mehr Daten durch Datenbearbeitung

Data Augmentation
- Mehr Daten -> grössere Modelle -> komplexere Aufgaben
- Mehr Daten durch Datenbearbeitung


Data Augmentation
- Mehr Daten -> grössere Modelle -> komplexere Aufgaben
- Mehr Daten durch Datenbearbeitung


Data Augmentation
- Mehr Daten -> grössere Modelle -> komplexere Aufgaben
- Mehr Daten durch Datenbearbeitung
- Verbessert Generalisierung
- Reduziert Overfitting


Regularisieren
Hands-On: MNIST Classifier
Bearbeiten Sie dieses Notebook
- Modifizieren Sie den MNIST Classifier
mit zwei Regularisierungen: Dropout & L2
- Vergleichen Sie die Performance
mit und ohne Regularisierung
Die Lösung finden Sie in diesem Notebook
Deep Learning
Möglichkeiten & Grenzen
Deep Learning
Möglichkeiten
Deep Learning
Möglichkeiten
- Automatisierung: Selbstfahrende Autos, Produktionsroboter, ...
Deep Learning
Möglichkeiten
- Automatisierung: Selbstfahrende Autos, Produktionsroboter, ...
- Datenanalyse: Vorhersage von Kundenverhalten, Betrugserkennung, ...
Deep Learning
Möglichkeiten
- Automatisierung: Selbstfahrende Autos, Produktionsroboter, ...
- Datenanalyse: Vorhersage von Kundenverhalten, Betrugserkennung, ...
- Entscheidungssysteme: Kreditvergabe, Diagnosesysteme, ...
Deep Learning
Möglichkeiten
- Automatisierung: Selbstfahrende Autos, Produktionsroboter, ...
- Datenanalyse: Vorhersage von Kundenverhalten, Betrugserkennung, ...
- Entscheidungssysteme: Kreditvergabe, Diagnosesysteme, ...
- Individualisierung: Personalisierte Werbung, individueller Support, ...
Deep Learning
Möglichkeiten
- Automatisierung: Selbstfahrende Autos, Produktionsroboter, ...
- Datenanalyse: Vorhersage von Kundenverhalten, Betrugserkennung, ...
- Entscheidungssysteme: Kreditvergabe, Diagnosesysteme, ...
- Individualisierung: Personalisierte Werbung, individueller Support, ...
- Optimierung: Logistik und Lieferkettenmanagement, Energieverbrauchsreduktion, ...
Deep Learning
Möglichkeiten
- Automatisierung: Selbstfahrende Autos, Produktionsroboter, ...
- Datenanalyse: Vorhersage von Kundenverhalten, Betrugserkennung, ...
- Entscheidungssysteme: Kreditvergabe, Diagnosesysteme, ...
- Individualisierung: Personalisierte Werbung, individueller Support, ...
- Optimierung: Logistik und Lieferkettenmanagement, Energieverbrauchsreduktion, ...
- Beschleunigung: Automatisierte Dokumentenprüfung, beschleunigte Datenverarbeitung, ...
Deep Learning
Gefahren
Deep Learning
Gefahren
- Datenschutz: Risiken bei Sammlung und Verwendung von Daten.
Deep Learning
Gefahren
- Datenschutz: Risiken bei Sammlung und Verwendung von Daten.
- Fehleranfälligkeit: Ungenauigkeiten oder Fehler in Vorhersagen, Halluzination, ...
Deep Learning
Gefahren
- Datenschutz: Risiken bei Sammlung und Verwendung von Daten.
- Fehleranfälligkeit: Ungenauigkeiten oder Fehler in Vorhersagen, Halluzination, ...
- Arbeitsmarktveränderungen: Risiken durch Automatisierung für Berufe und Branchen.
Deep Learning
Gefahren
- Datenschutz: Risiken bei Sammlung und Verwendung von Daten.
- Fehleranfälligkeit: Ungenauigkeiten oder Fehler in Vorhersagen, Halluzination, ...
- Arbeitsmarktveränderungen: Risiken durch Automatisierung für Berufe und Branchen.
- Transparenz: Entscheidungsprozessen schwer nachvollziehbar.
Deep Learning
Gefahren
- Datenschutz: Risiken bei Sammlung und Verwendung von Daten.
- Fehleranfälligkeit: Ungenauigkeiten oder Fehler in Vorhersagen, Halluzination, ...
- Arbeitsmarktveränderungen: Risiken durch Automatisierung für Berufe und Branchen.
- Transparenz: Entscheidungsprozessen schwer nachvollziehbar.
- Desinformation, Manipulation: Missbrauch, Deepfakes, ...
Deep Learning
Gefahren
- Datenschutz: Risiken bei Sammlung und Verwendung von Daten.
- Fehleranfälligkeit: Ungenauigkeiten oder Fehler in Vorhersagen, Halluzination, ...
- Arbeitsmarktveränderungen: Risiken durch Automatisierung für Berufe und Branchen.
- Transparenz: Entscheidungsprozessen schwer nachvollziehbar.
- Desinformation, Manipulation: Missbrauch, Deepfakes, ...
- Verstärkung von Ungleichheiten: durch Voreingenommenheiten in Daten.
Deep Learning
Grenzen
- Datenabhängigkeit: Benötigt große Datenmengen.

Deep Learning
Grenzen
- Datenabhängigkeit: Benötigt große Datenmengen.

Curse of Dimensionality
Abstände zwischen den Datenpunkten steigen exponentiell mit Dimension
Benötigte Anzahl Daten steigt Exponentiell mit Anzahl extrahierter Informationen
Deep Learning
Grenzen
- Datenabhängigkeit: Benötigt große Datenmengen.
- Rechenintensität: Erfordert erhebliche Rechenleistung und Ressourcen.
Deep Learning
Grenzen
- Datenabhängigkeit: Benötigt große Datenmengen.
- Rechenintensität: Erfordert erhebliche Rechenleistung und Ressourcen.
- Überanpassung: Risiko der zu spezifischen Anpassung an Trainingsdaten.
Deep Learning
Grenzen
- Datenabhängigkeit: Benötigt große Datenmengen.
- Rechenintensität: Erfordert erhebliche Rechenleistung und Ressourcen.
- Überanpassung: Risiko der zu spezifischen Anpassung an Trainingsdaten.
- Mangelnde Erklärbarkeit: Entscheidungsprozesse sind oft nicht nachvollziehbar.
Deep Learning
Grenzen
- Datenabhängigkeit: Benötigt große Datenmengen.
- Rechenintensität: Erfordert erhebliche Rechenleistung und Ressourcen.
- Überanpassung: Risiko der zu spezifischen Anpassung an Trainingsdaten.
- Mangelnde Erklärbarkeit: Entscheidungsprozesse sind oft nicht nachvollziehbar.
- Bias-Verstärkung: Potenzielle Verstärkung von in Daten vorhandenen Vorurteilen.
Deep Learning
Grenzen
- Datenabhängigkeit: Benötigt große Datenmengen.
- Rechenintensität: Erfordert erhebliche Rechenleistung und Ressourcen.
- Überanpassung: Risiko der zu spezifischen Anpassung an Trainingsdaten.
- Mangelnde Erklärbarkeit: Entscheidungsprozesse sind oft nicht nachvollziehbar.
- Bias-Verstärkung: Potenzielle Verstärkung von in Daten vorhandenen Vorurteilen.
- Generalisierungsproblem: Schwierigkeiten bei neuartigen Daten.
Optimieren
Optimieren
Optimieren

Modell auf unbekannten Daten optimieren
aber
Testset erst ganz zum Schluss verwenden
Train-Test-Valid Split
Modell auf unbekannten Daten optimieren
aber
Testset erst ganz zum Schluss verwenden
Weiteres Datenset absplitten
Train-Test-Valid Split
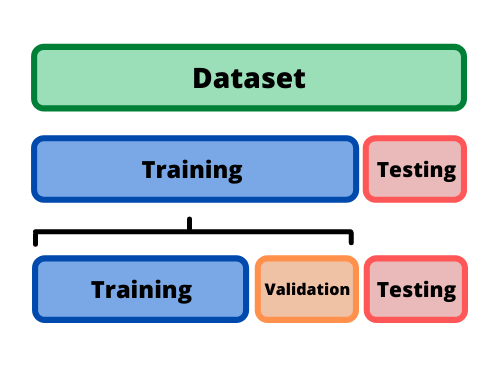
Train-Test-Valid Split

- verschiedene Settings wählen (Hyperparameter / Architektur)
- für wenige Epochen trainieren
- Leistung auf Validationsdaten vergleichen
- Setting mit bester Leistung voll trainieren
- Trainiertes Modell auf Testset Evaluieren
Train-Test-Valid Split

- verschiedene Settings wählen (Hyperparameter / Architektur)
- für wenige Epochen trainieren
- Leistung auf Validationsdaten vergleichen
- Setting mit bester Leistung voll trainieren
- Trainiertes Modell auf Testset Evaluieren
from torch.utils.data import random_split
train_ratio, valid_ratio = 0.8, 0.2
# Gesamteanzahl der Trainingsdaten
N_training = len(training_data)
# Berechne die Anzahl der Beispiele für jeden Split
train_size = int(train_ratio * N_training)
valid_size = N_training - train_size
# Teile den Trainingsdatensatz in Train und Valid auf
train_data, valid_data = random_split(training_data,
[train_size, valid_size])
Train-Test-Valid Split

- verschiedene Settings wählen (Hyperparameter / Architektur)
- für wenige Epochen trainieren
- Leistung auf Validationsdaten vergleichen
- Setting mit bester Leistung voll trainieren
- Trainiertes Modell auf Testset Evaluieren
from torch.utils.data import random_split
train_ratio, valid_ratio = 0.8, 0.2
# Gesamteanzahl der Trainingsdaten
N_training = len(training_data)
# Berechne die Anzahl der Beispiele für jeden Split
train_size = int(train_ratio * N_training)
valid_size = N_training - train_size
# Teile den Trainingsdatensatz in Train und Valid auf
train_data, valid_data = random_split(training_data,
[train_size, valid_size])
import tensorflow as tf
from sklearn.model_selection import train_test_split
valid_ratio = 0.2
input_data = your_input_data
labels = your_labels
input_train, input_valid, labels_train, labels_valid =
train_test_split(input_data, labels, test_size=valid_ratio, random_state=42)
# Create TensorFlow Datasets
train_dataset = tf.data.Dataset.from_tensor_slices((input_train, labels_train))
valid_dataset = tf.data.Dataset.from_tensor_slices((input_valid, labels_valid))
Hyperparameter

Hyperparameter

class MLP_var(nn.Module):
def __init__(self, N_layer: int):
super(MLP_var, self).__init__()
layers = []
layers.append(nn.Linear(28*28, 64))
layers.append(nn.ReLU())
for _ in range(N_layer-1):
layers.append(nn.Linear(64, 64))
layers.append(nn.ReLU())
layers.append(nn.Linear(64, 10))
self.model = nn.Sequential(*layers)
def forward(self, x):
x = x.view(x.size(0), -1)
x = self.model(x)
return x
Hyperparameter Search

Hyperparameter Search
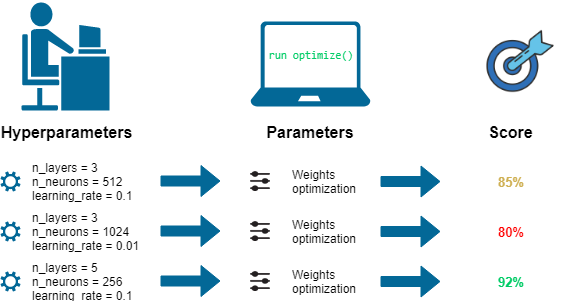
Try different Values, pick best score
Hyperparameter Search
Try different Values, pick best score
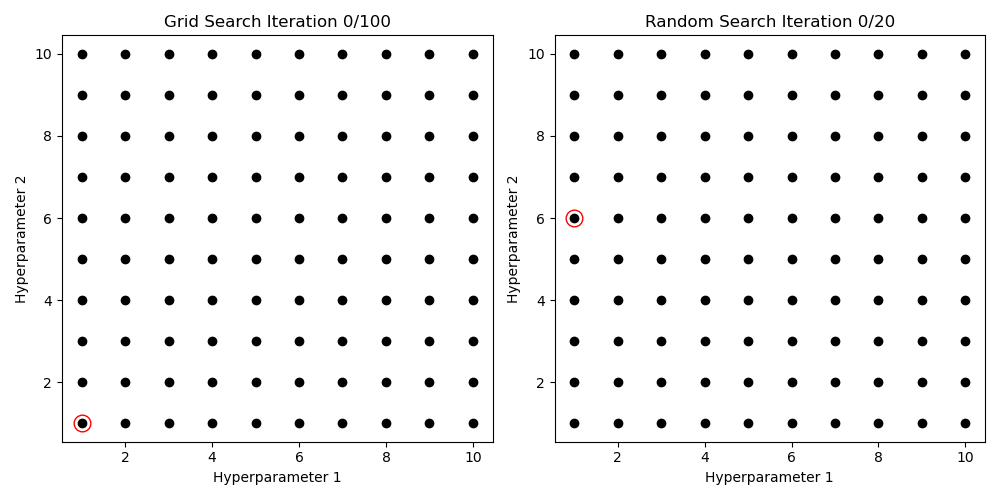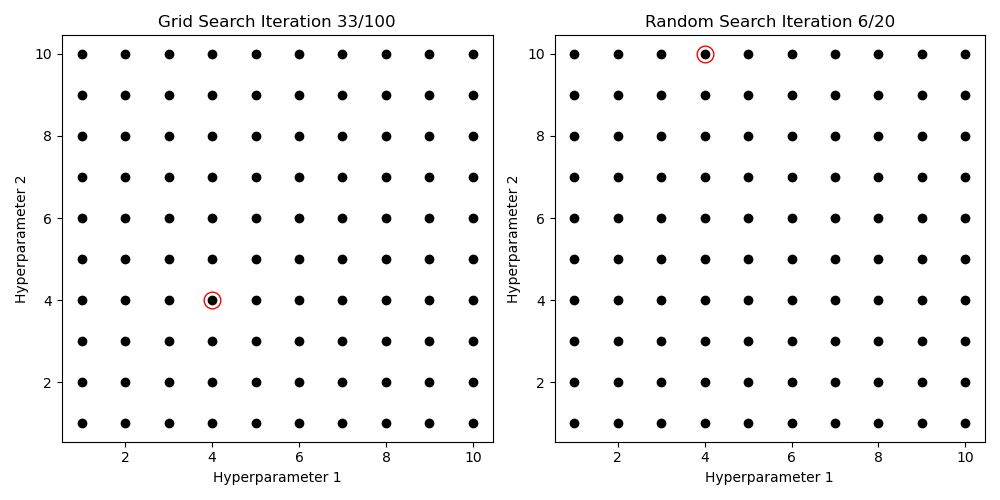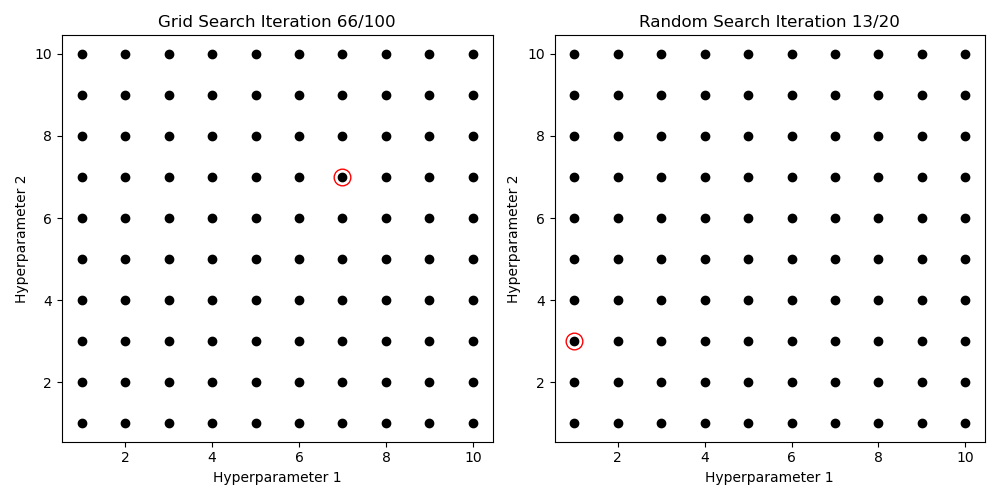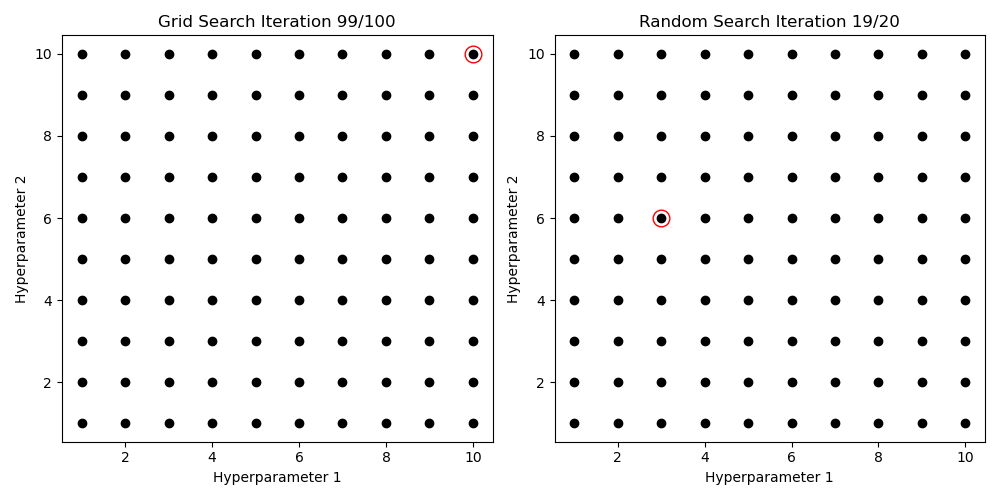

Hyperparameter Search
Gridsearch


for (N_layer, lr) in product(N_layer_values, learning_rate_values):
model = MLP_var(N_layer)
model.to(device)
criterion = nn.CrossEntropyLoss()
optimizer = optim.Adam(model.parameters(), lr=lr)
losses_train, losses_valid, f1_scores_train, f1_scores_valid = full_training(
model, criterion, optimizer, training_loader, valid_loader, epochs=epochs
)Einfluss auf Stabilität
Regularisierung
Hyperparameter
Tuning
Optimizer
Aufwand
Hyperparameter
Tuning
Optimizer
Regularisierung
Optimieren
Hands-On: MNIST Classifier
Bearbeiten Sie dieses Notebook
- Erstellen Sie einen MNIST Classifier
mit variabler Anzahl hidden Layer
- Erstellen Sie einen Validationsdatensatz
- Führen sie ein Hyperparametertuning durch
Die Lösung finden Sie in diesem Notebook
Deep Learning
Anwendungen
-
Computer Vision: Klassifizierung, Objekterkennung, Bildgenerierung
-
Natural Language Processing: Übersetzungen, Chatbots
-
Reinforcement Learning: Gaming, Robotik, Automatisierung
-
Zeitreihenanalyse: Markt- & Wetterprognosen, Anomalieerkennung
-
Explainable AI: Transparenz, Vertrauen, Sicherheit
Deep Learning
Anwendungen
-
Computer Vision: Klassifizierung, Objekterkennung, Bildgenerierung

Deep Learning
Computer Vision

Convolutional Neural Network (CNN)
Findet Strukturen
Deep Learning
Computer Vision

Convolutional Neural Network (CNN)
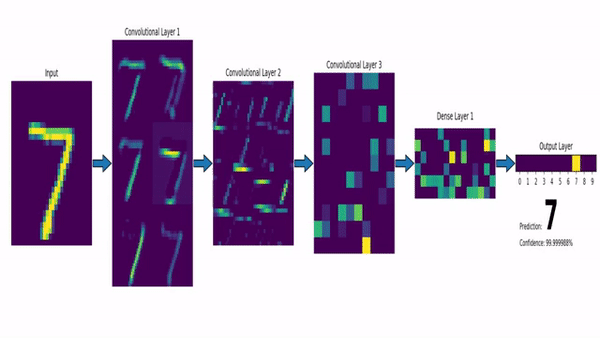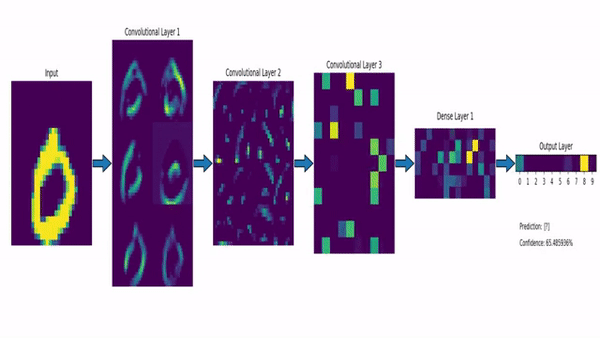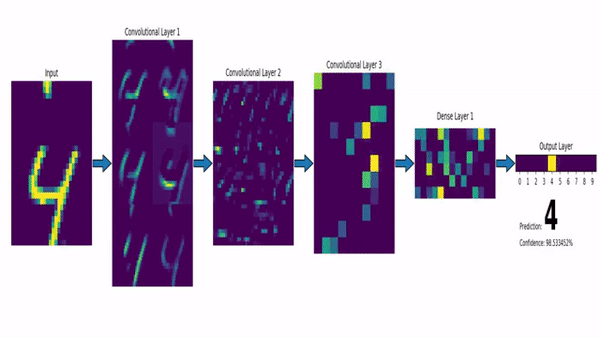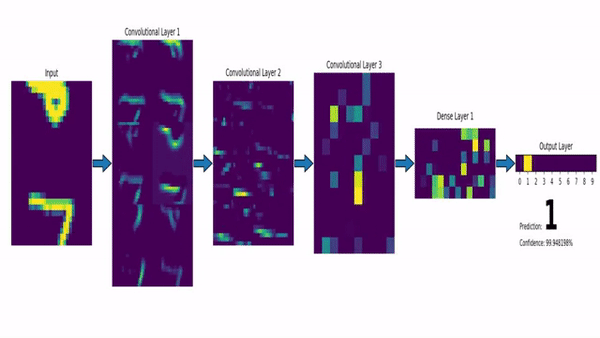
Klassifiziert durch Strukturen
Deep Learning
Generative Modelle

Erstellen neue Daten wie Trainingsdaten
aus Zufalls-zahlen
Varational Autoencoder
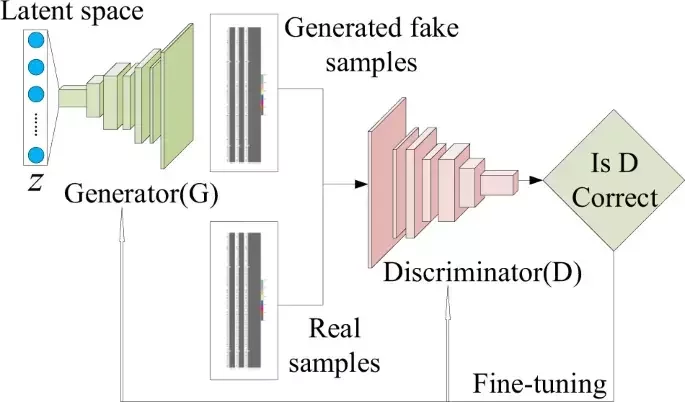
Generative Adversarial Network
Deep Learning
Varational Autoencoder
- Entfernt schrittweise Rauschen (Noise)
um darunter liegendes Bild zu enthüllen
- kann aus reinem Rauschen neue Bilder generieren
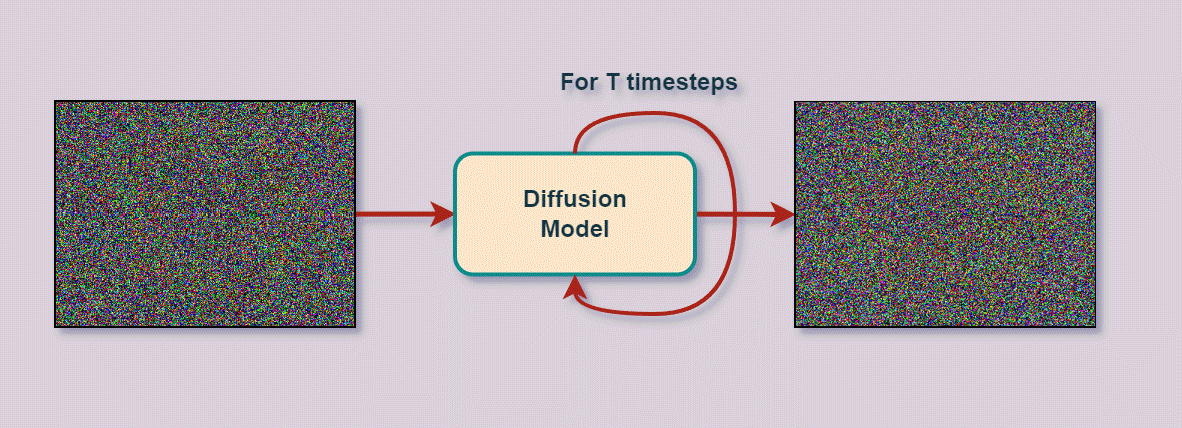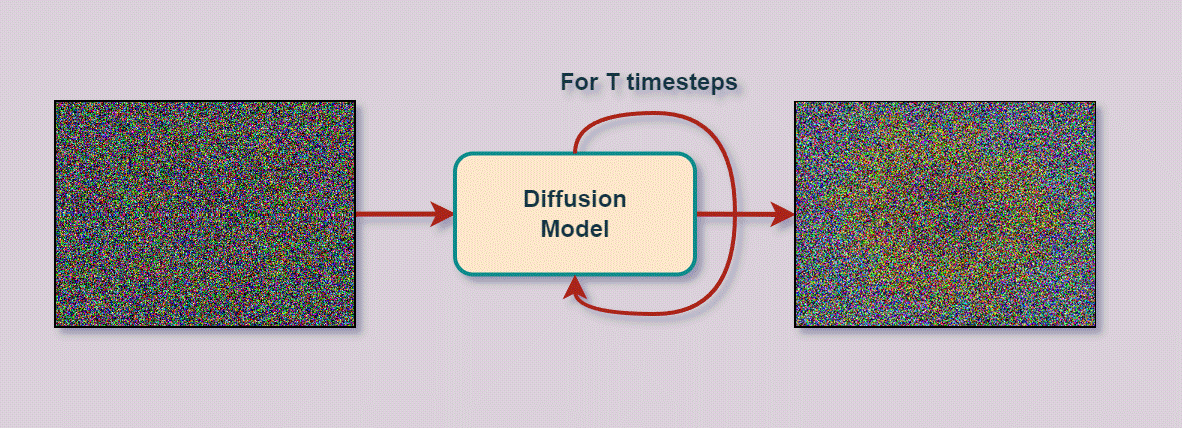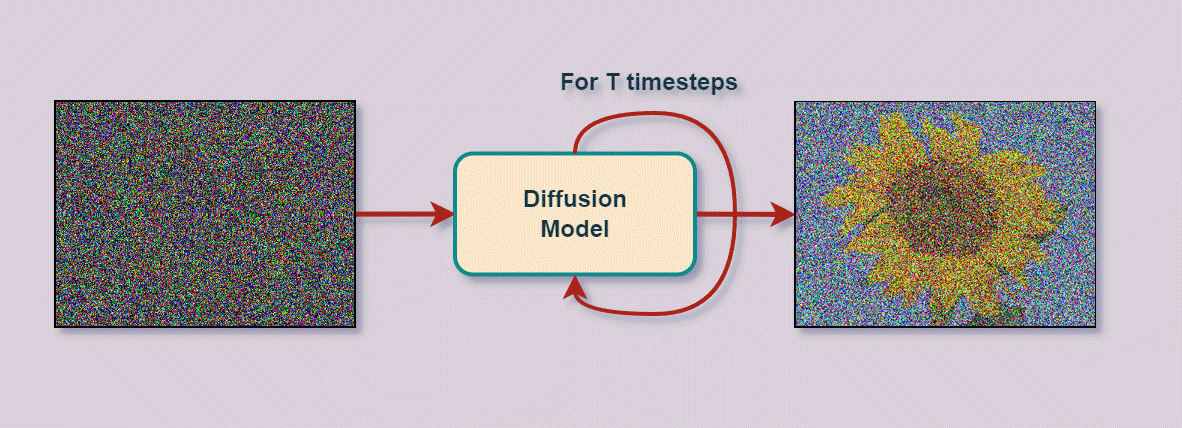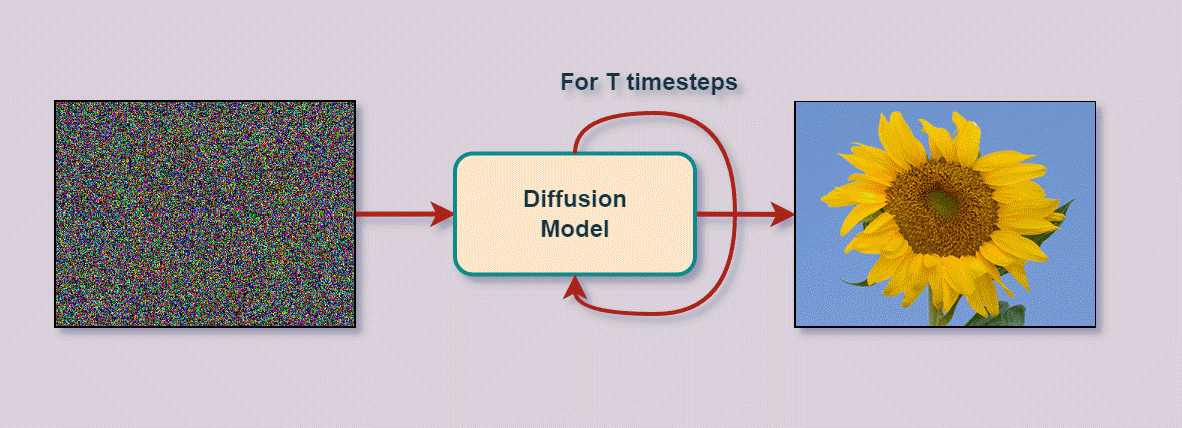
Deep Learning
Anwendungen
-
Computer Vision: Klassifizierung, Objekterkennung, Bildgenerierung
-
Natural Language Processing: Übersetzungen, Chatbots
-
Reinforcement Learning: Gaming, Robotik, Automatisierung
-
Zeitreihenanalyse: Markt- & Wetterprognosen, Anomalieerkennung
-
Explainable AI: Transparenz, Vertrauen, Sicherheit
Deep Learning
Anwendungen
-
Natural Language Processing: Übersetzungen, Chatbots

Deep Learning
Natural Language Processing
Sprachverarbeitung Wort für Wort
Wie in Kontext setzen?
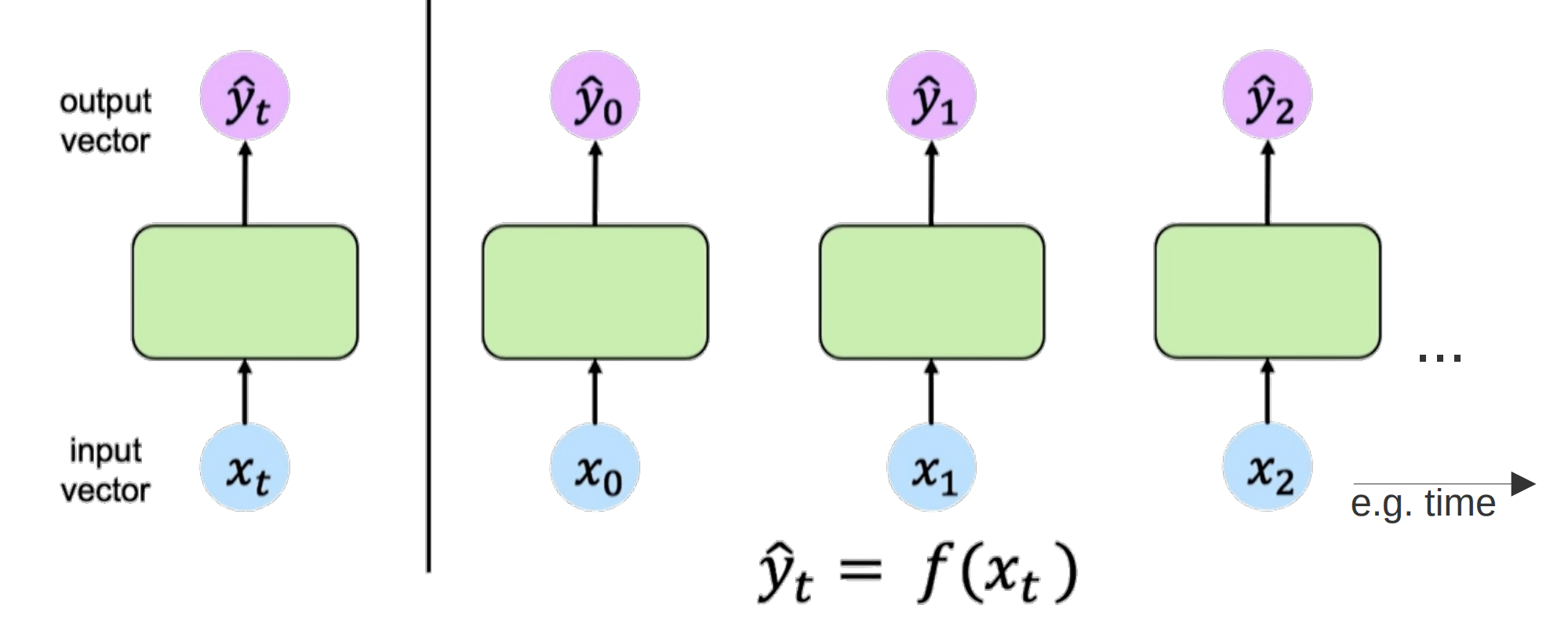
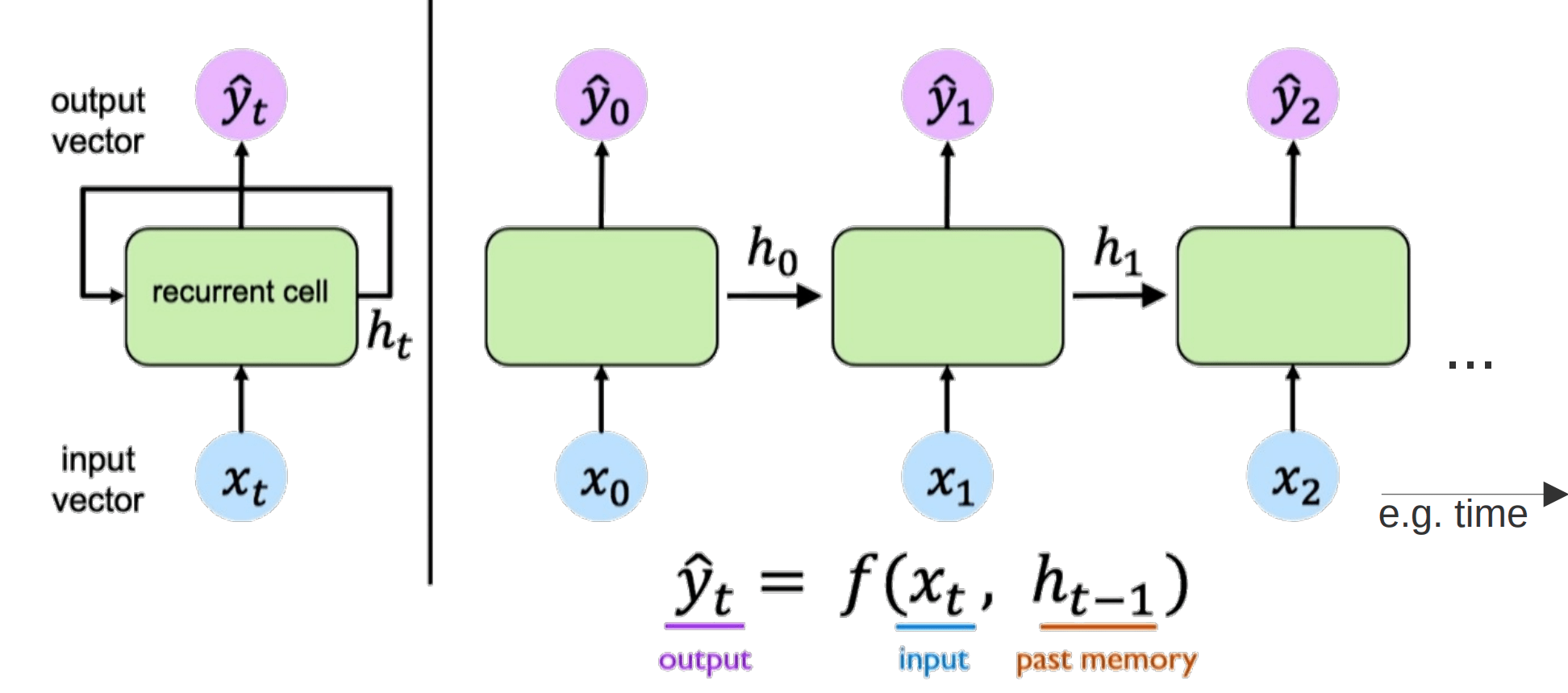
RNN

Deep Learning
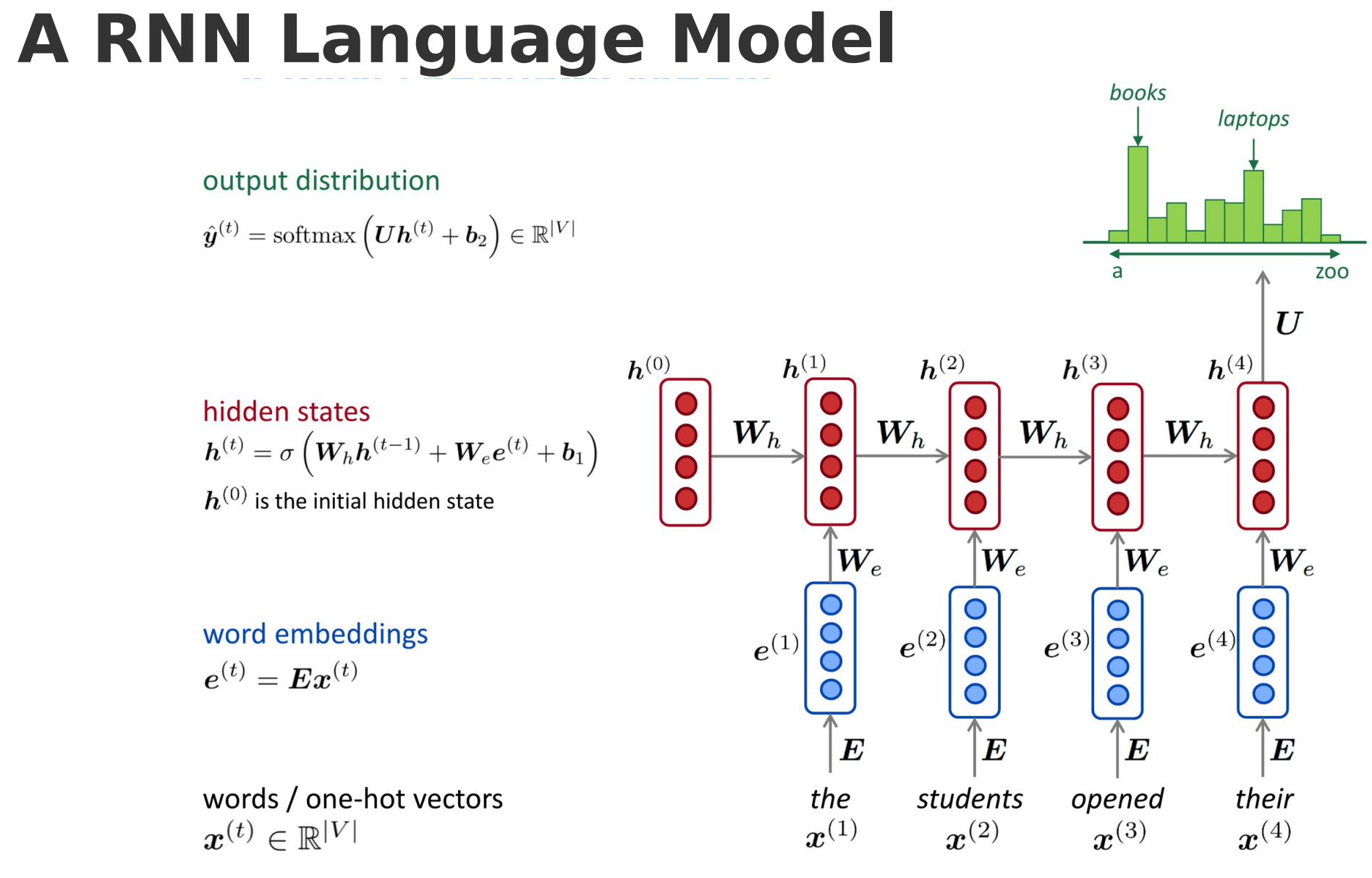
Natural Language Processing
Recurrent Neural Network (RNN)

Liest Satz Wort für Wort
Selbe Weights für jedes Wort
Deep Learning
Natural Language Processing

Liest Satz Wort für Wort
keine Parallelisierung
Deep Learning
Natural Language Processing
Transformer
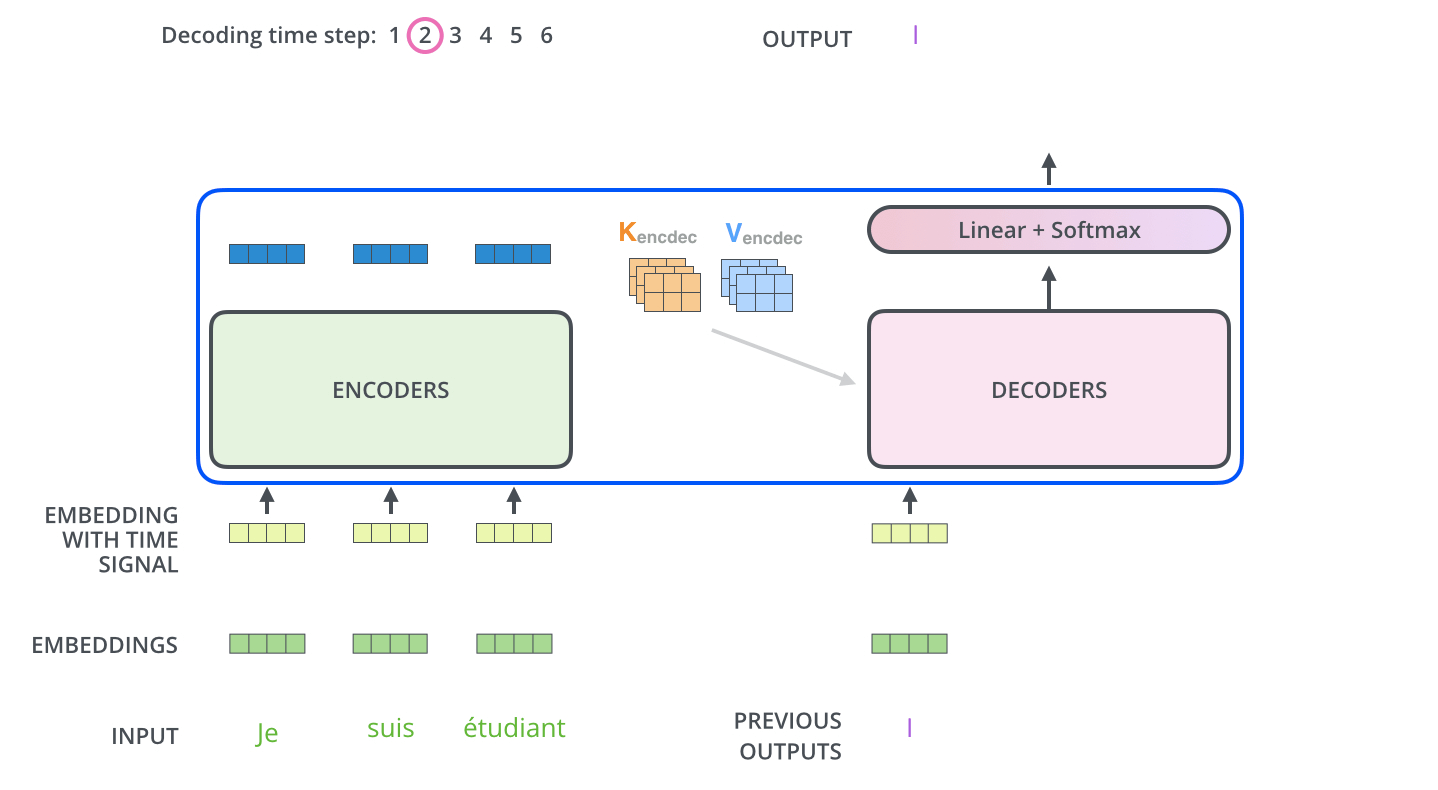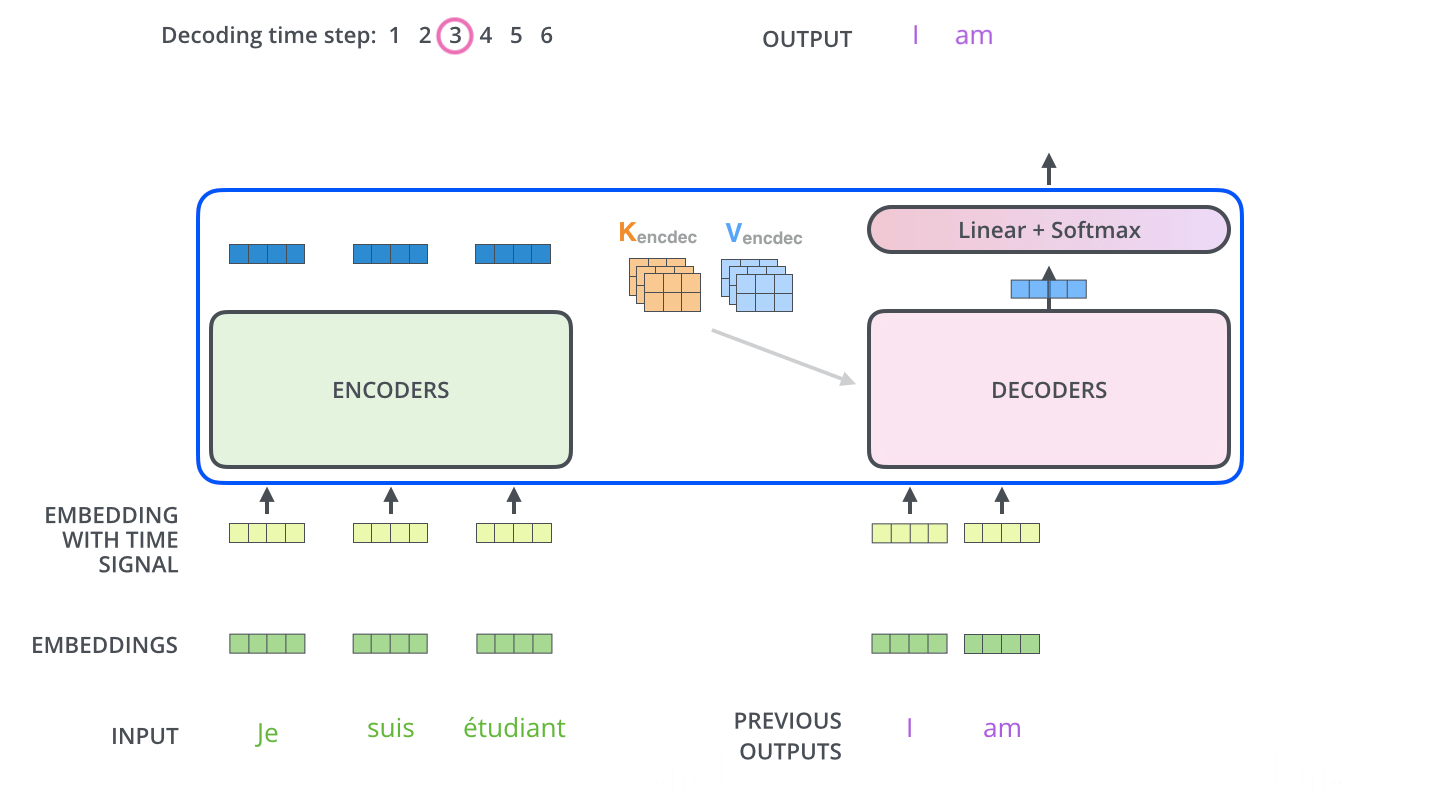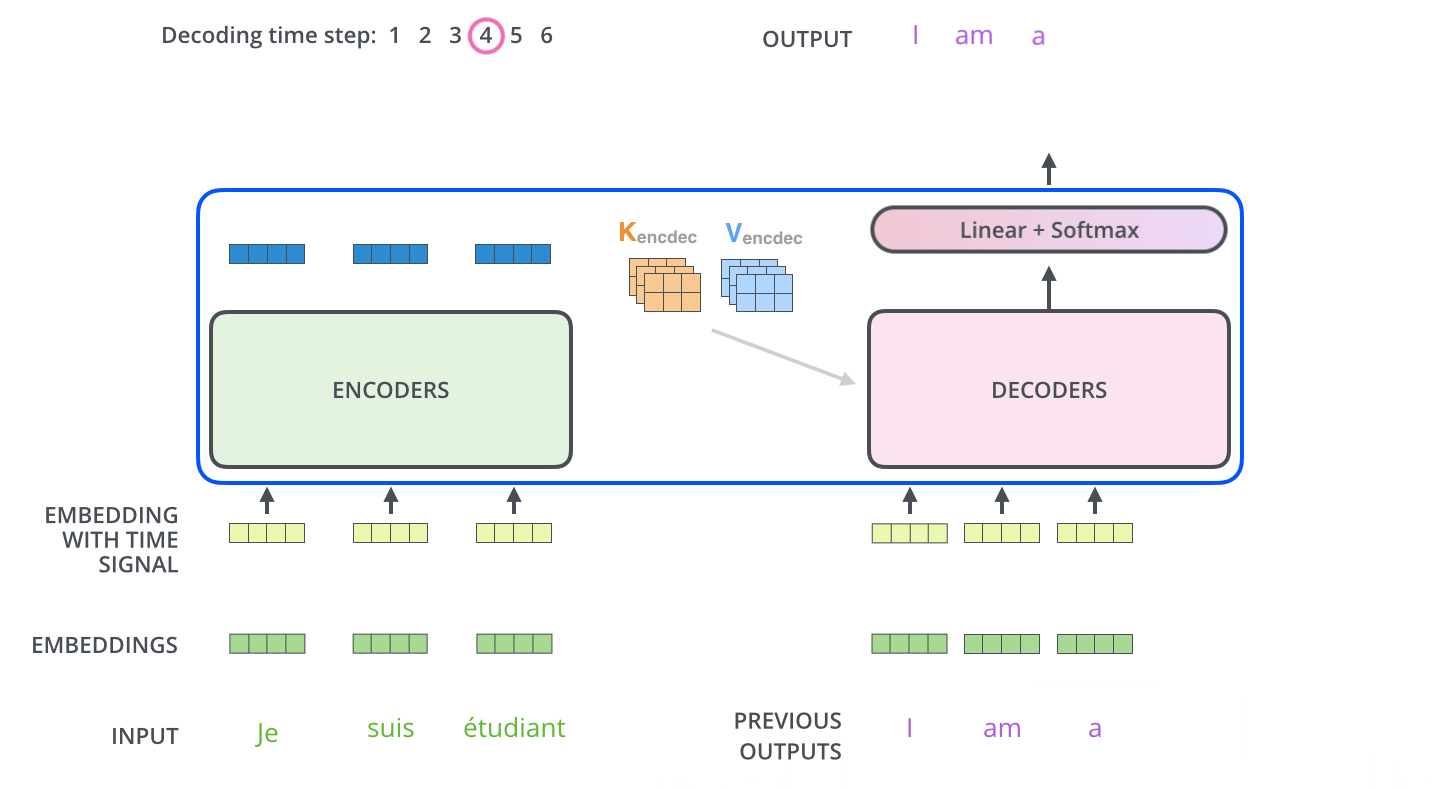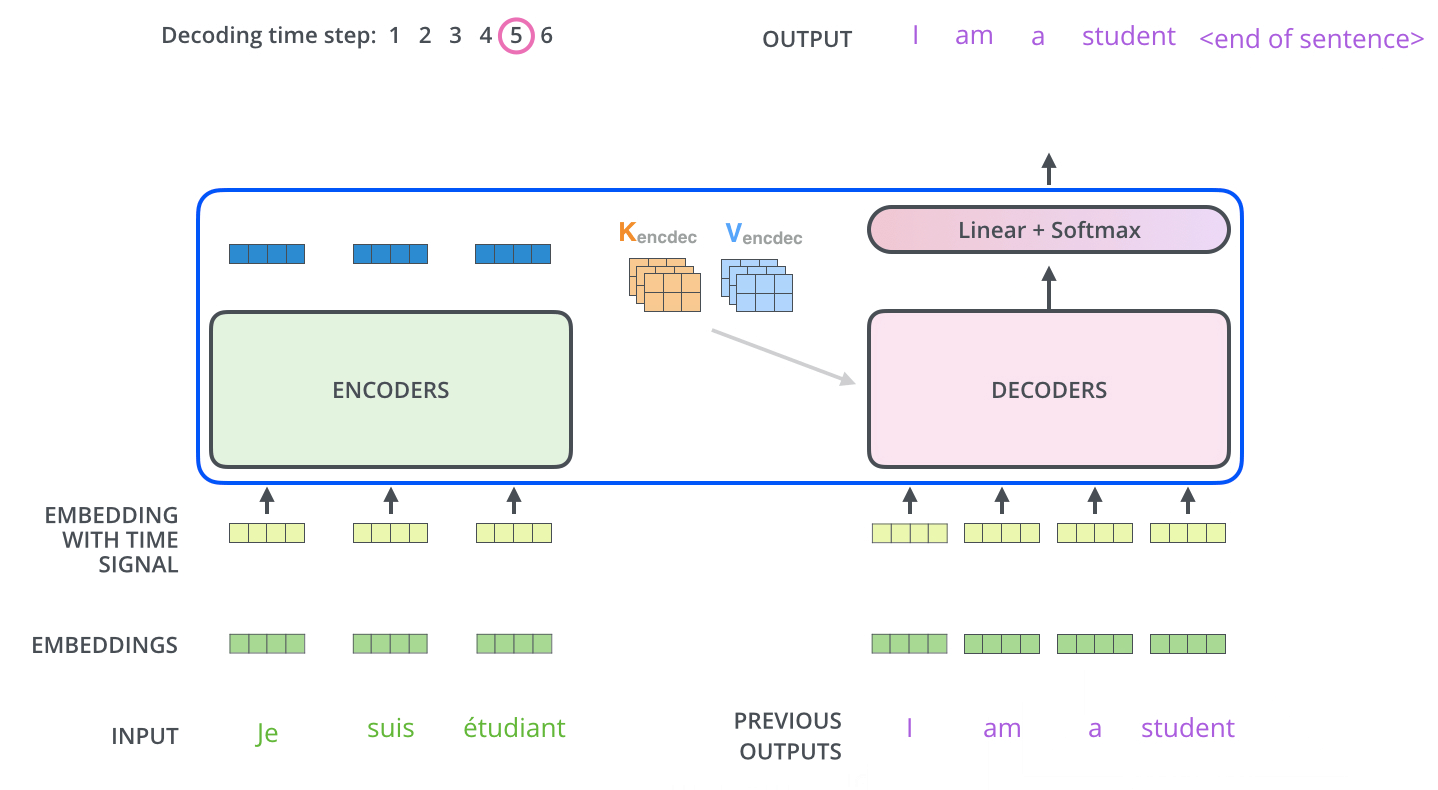
Transformiert Sequenz zu neuer Sequenz
Deep Learning
Natural Language Processing

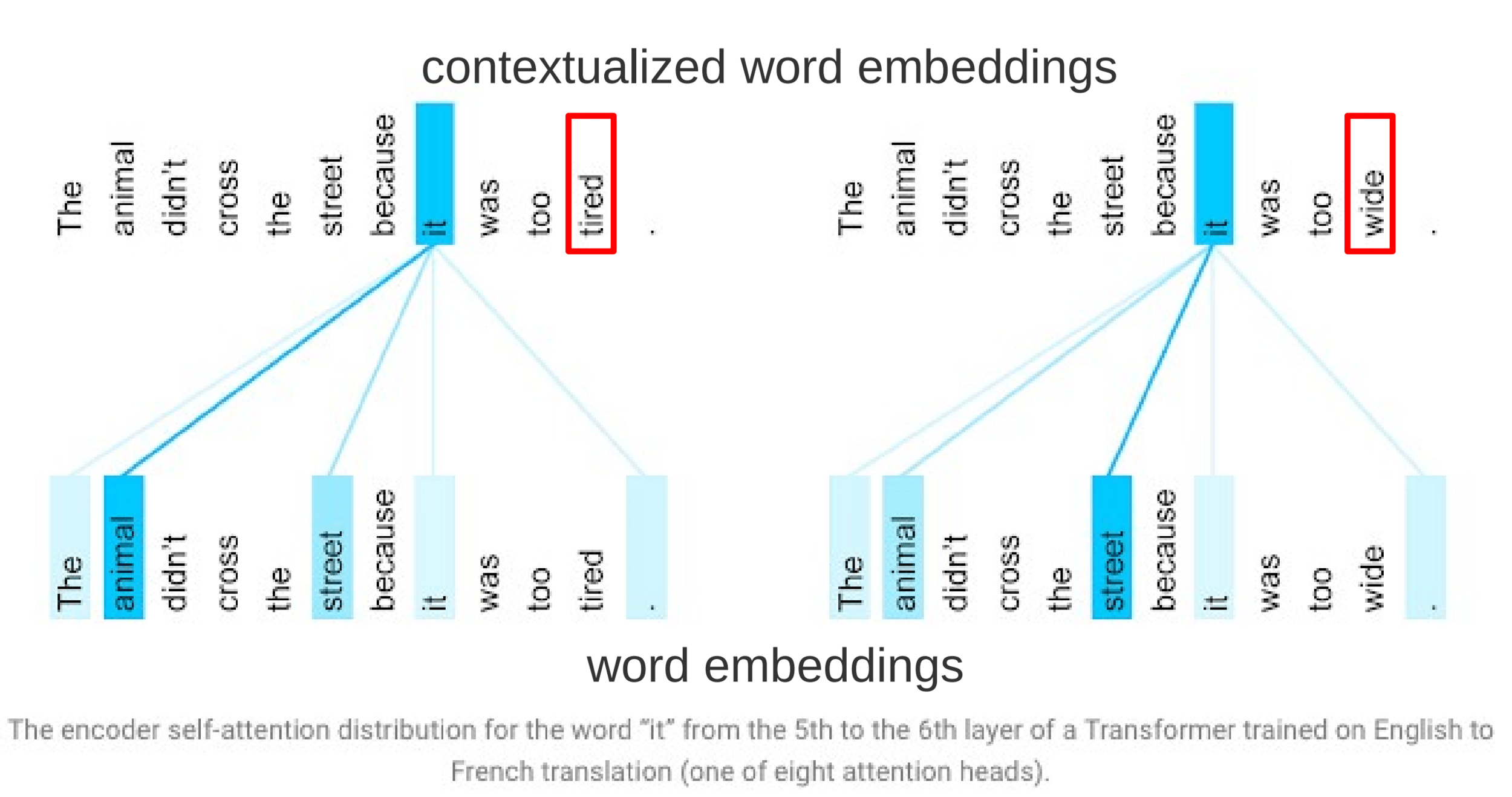
Attention layer lernt Kontext
als Stärke der Beziehung von Wörtern

Transformer
Deep Learning
Natural Language Processing
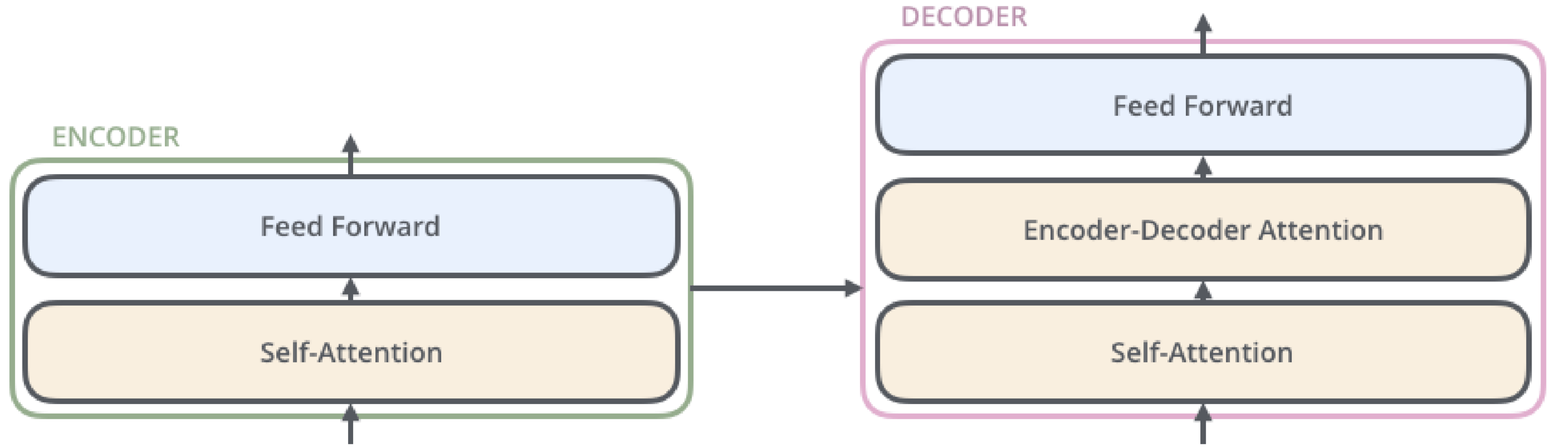
Transformer


Stacks von Encodern / Decodern
Erlaubt Parallelisierung
Deep Learning
Natural Language Processing
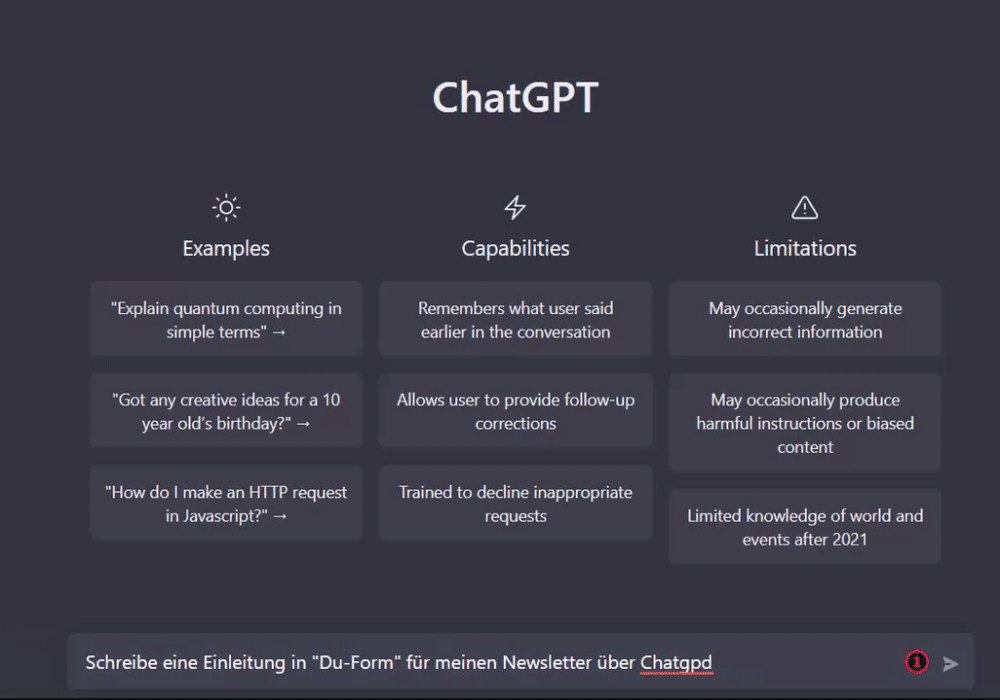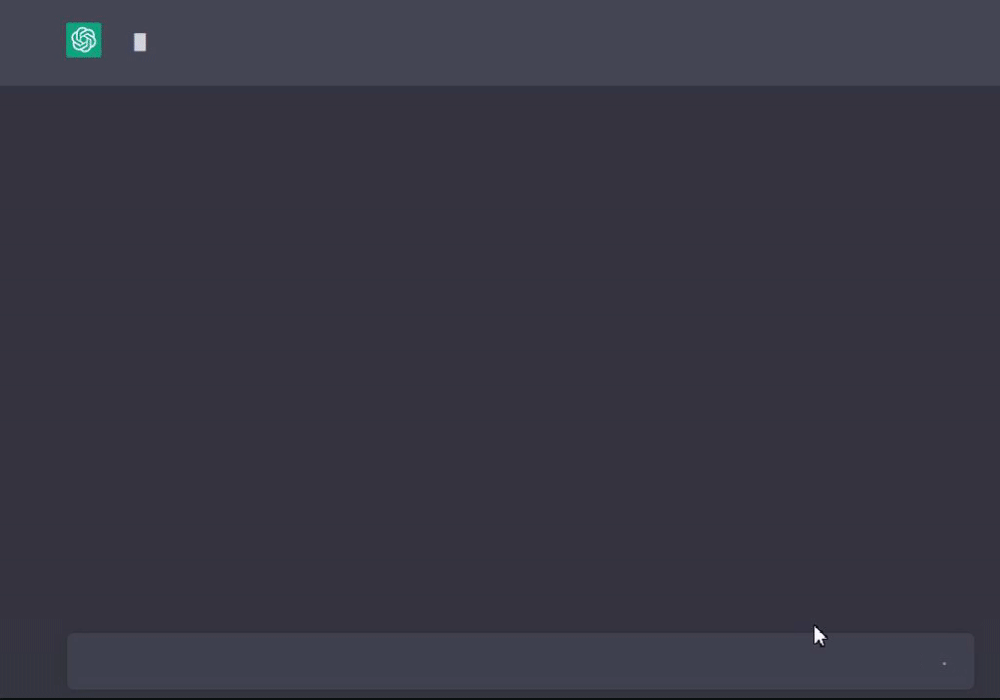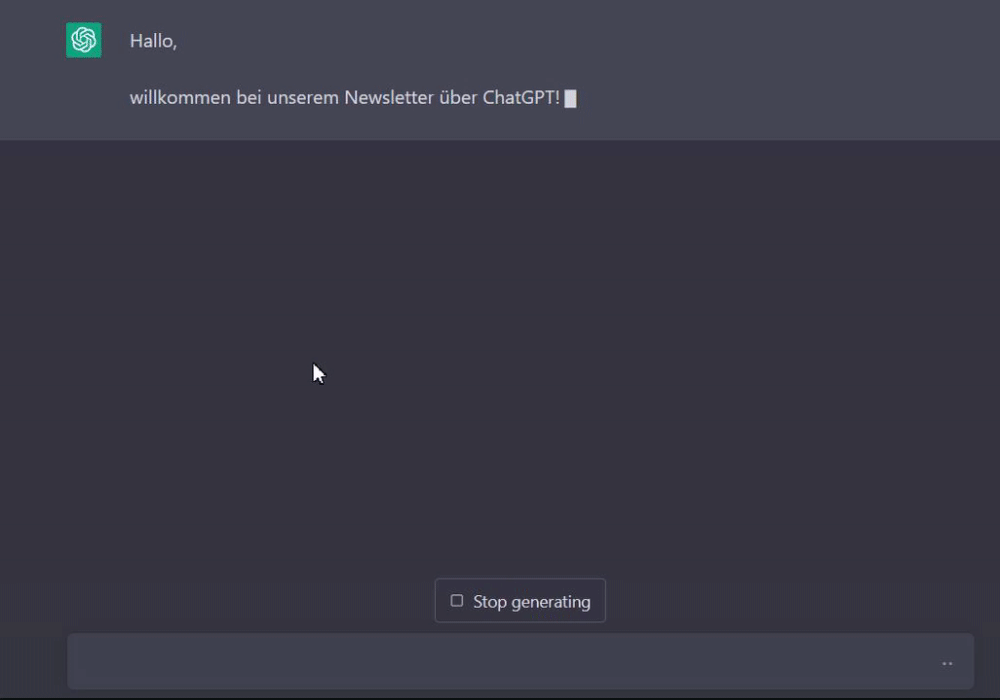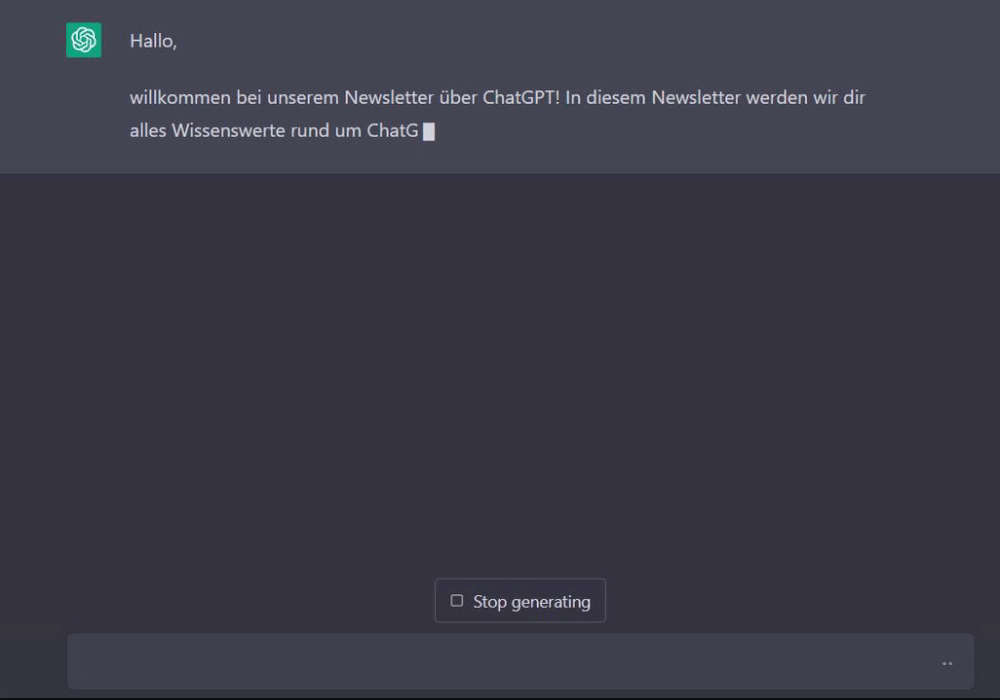
Transformer

- Autovervollständigung
- Übersetzung
- Chatbots
Deep Learning
Anwendungen
-
Computer Vision: Klassifizierung, Objekterkennung, Bildgenerierung
-
Natural Language Processing: Übersetzungen, Chatbots
-
Reinforcement Learning: Gaming, Robotik, Automatisierung
-
Zeitreihenanalyse: Markt- & Wetterprognosen, Anomalieerkennung
-
Explainable AI: Transparenz, Vertrauen, Sicherheit
Deep Learning
Anwendungen
-
Reinforcement Learning: Gaming, Robotik, Automatisierung

Deep Learning
Reinforcement Learning

Findet versprechendste Aktion in beliebigem Zustand
Deep Learning
Reinforcement Learning
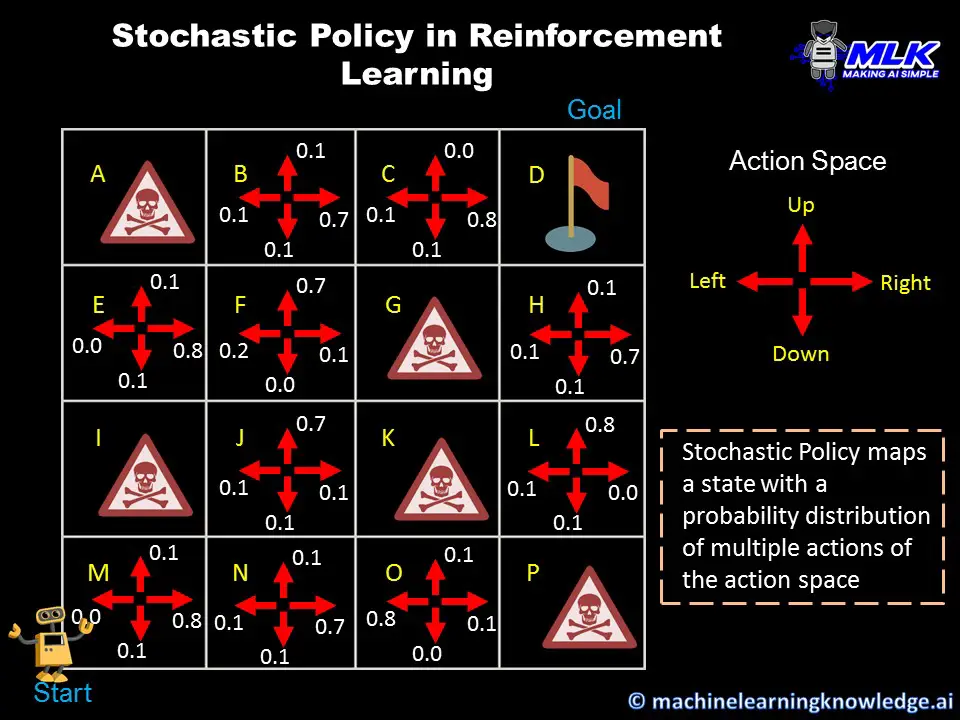
Hin und wieder neues ausprobieren
-> auf Veränderung reagieren
Deep Learning
Reinforcement Learning

Hin und wieder neues ausprobieren
-> auf Veränderung reagieren
Es ist gut Fehler zu machen!
Deep Learning
Reinforcement Learning

Früher: Tabelle
Heute:
Neuronales Netz
Deep Learning
Anwendungen
-
Computer Vision: Klassifizierung, Objekterkennung, Bildgenerierung
-
Natural Language Processing: Übersetzungen, Chatbots
-
Reinforcement Learning: Gaming, Robotik, Automatisierung
-
Zeitreihenanalyse: Markt- & Wetterprognosen, Anomalieerkennung
-
Explainable AI: Transparenz, Vertrauen, Sicherheit
Deep Learning
Anwendungen
-
Zeitreihenanalyse: Markt- & Wetterprognosen, Anomalieerkennung

Deep Learning
Zeitreihenanalyse

Kurzzeit-
Gedächtnis
Text
Langes
Kurzzeit-
Gedächtnis
Deep Learning
Layer

| Fully Connected (Dense) |
|---|
| Alle Neuronen verbunden |
| Lineare Approximation |
| Merkmale -> Klassifizierung |
| Viele lernbare Parameter (In x Out) |
| Hoher Rechenaufwand |
Deep Learning
Layer

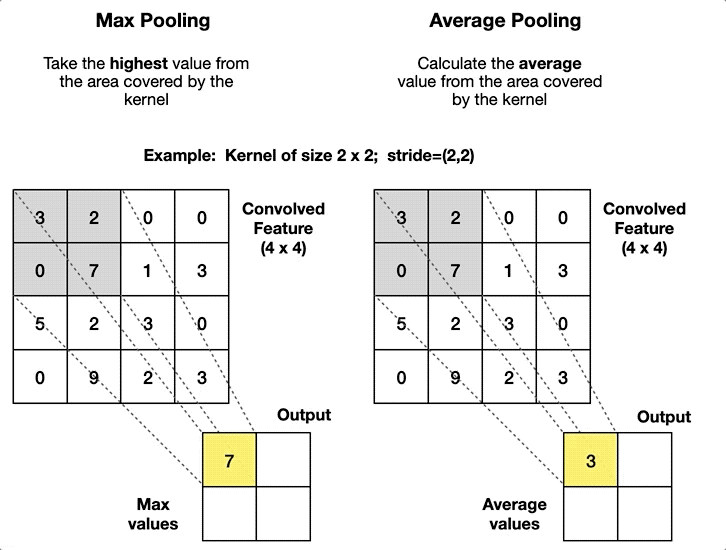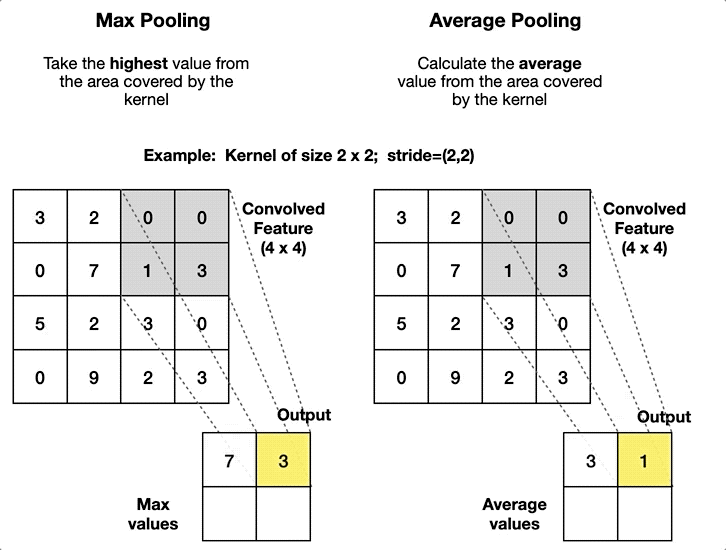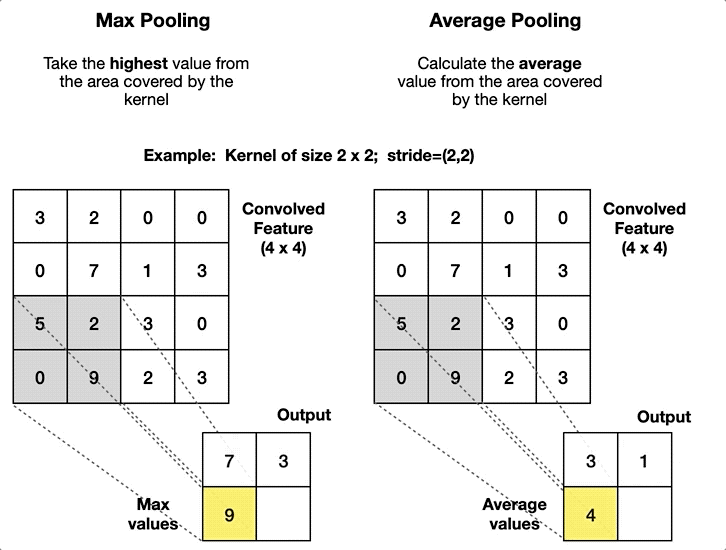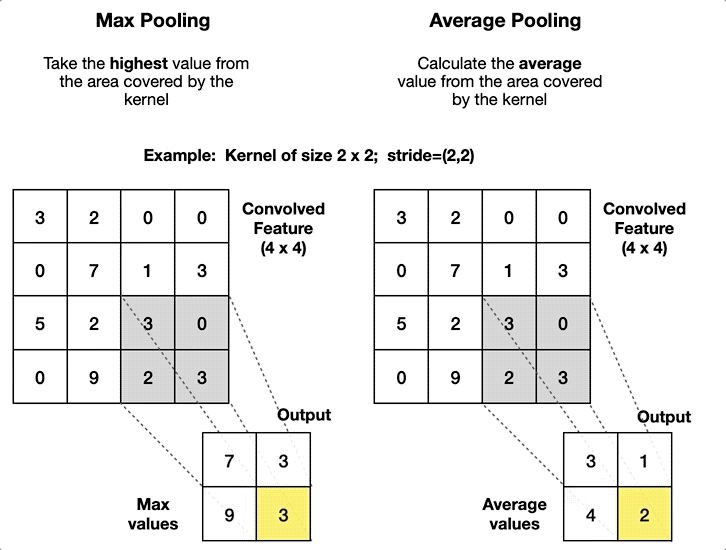
| Fully Connected (Dense) | Pooling (Pool) |
|---|---|
| Alle Neuronen verbunden | Filtert informationen |
| Lineare Approximation | Grössenreduktion |
| Merkmale -> Klassifizierung | Robustere Modelle |
| Viele lernbare Parameter (In x Out) | Keine Lernparameter |
| Hoher Rechenaufwand | Geringer Rechenaufwand |
Deep Learning
Layer


| Fully Connected (Dense) | Pooling (Pool) | Convolutional (Conv) |
|---|---|---|
| Alle Neuronen verbunden | Filtert informationen | Gelernter Filter gleiteit über Daten |
| Lineare Approximation | Grössenreduktion | Extrahiert lokale Merkmale |
| Merkmale -> Klassifizierung | Robustere Modelle | Mustererkennung |
| Viele lernbare Parameter (In x Out) | Keine Lernparameter | wenige lernbare Parameter |
| Hoher Rechenaufwand | Geringer Rechenaufwand | Geringer Rechenaufwand |

Deep Learning
Layer - Typische Anordnung


| Convolutional (Conv) | Pooling (Pool) | Fully Connected (Dense) |
|---|---|---|
| Extrahiert lokale Merkmale | Filtert informationen | Merkmale -> Klassifizierung |
| wenige lernbare Parameter | Robustere Modelle |

Effizienteres Modell Translationsinvariant Bessere Generalisierung
Layer
Hands-On: TensorFlow CIFAR-10
Starten Sie mit diesem Notebook
- Klasifizieren Sie den CIFAR-100
- Vergleichen Sie verschiedene Regularisationsmethoden an CNN
- Führen Sie ein Hyperparametertuning durch
Die Lösung finden Sie in diesem Notebook
Deep Learning Geschichte


Deep Learning Geschichte


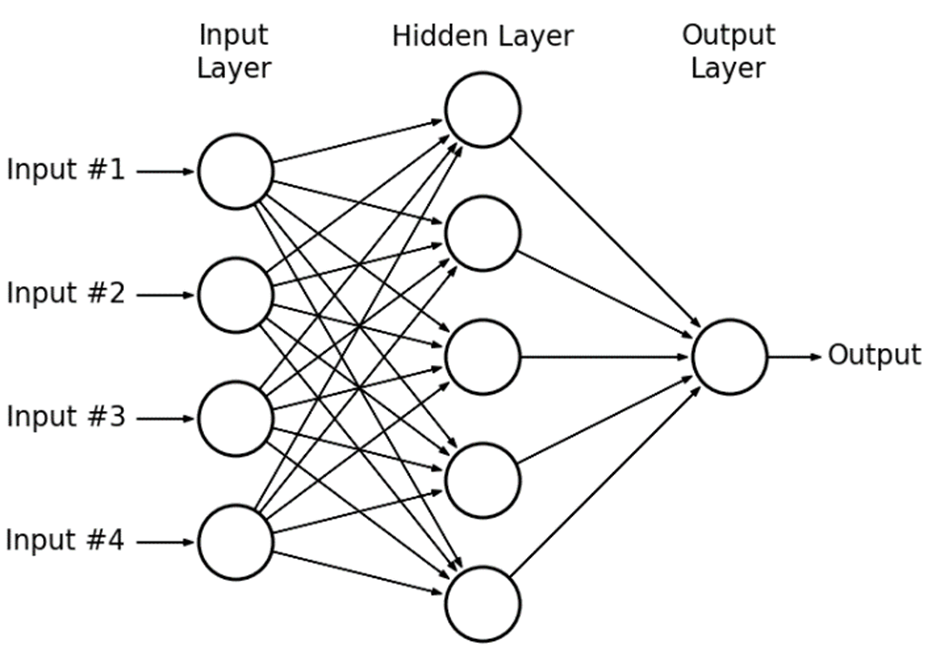





Single Layer Perceptron
Deep Learning Geschichte










Deep Learning Geschichte










Multilayer Perceptron
Deep Learning Geschichte










Deep Learning Geschichte










Recurrent Neural Network (RNN)
Deep Learning Geschichte










Deep Learning Geschichte










Convolutional Neural Network (CNN)
Deep Learning Geschichte






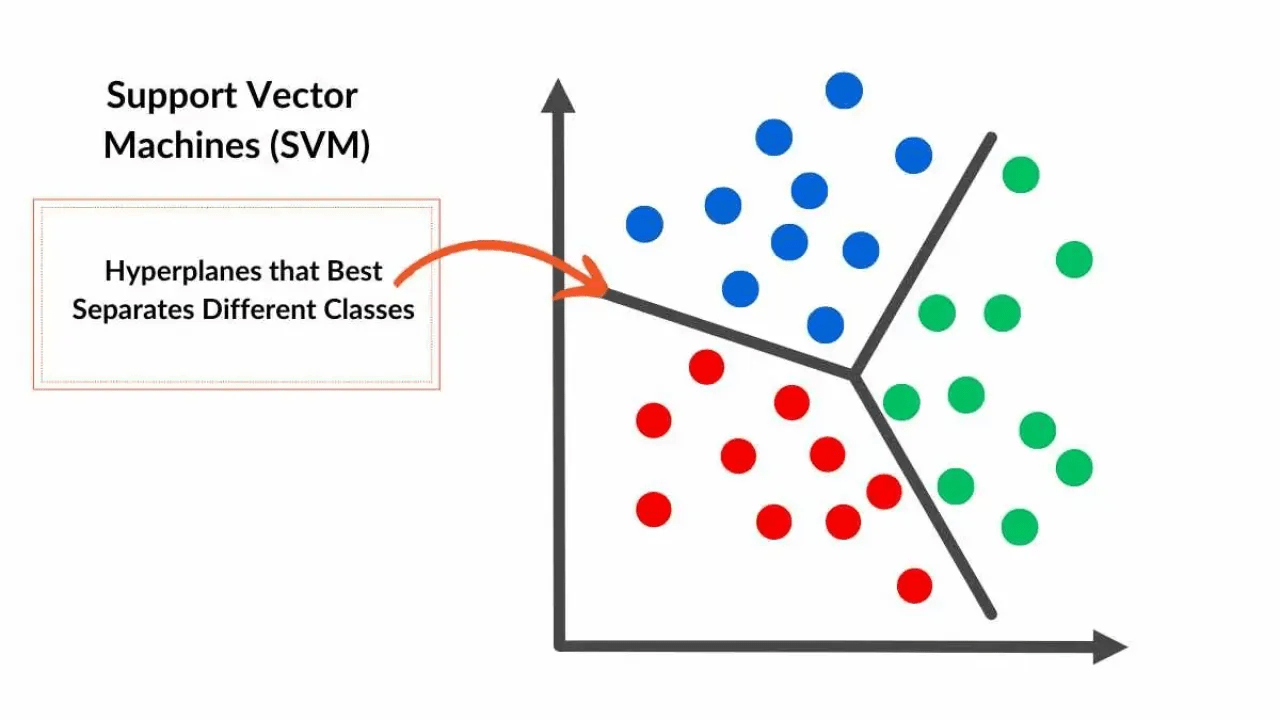




Deep Learning Geschichte











Support Vector Machines
Deep Learning Geschichte











Deep Learning Geschichte











Autoencoder
Deep Learning Geschichte











Deep Learning Geschichte











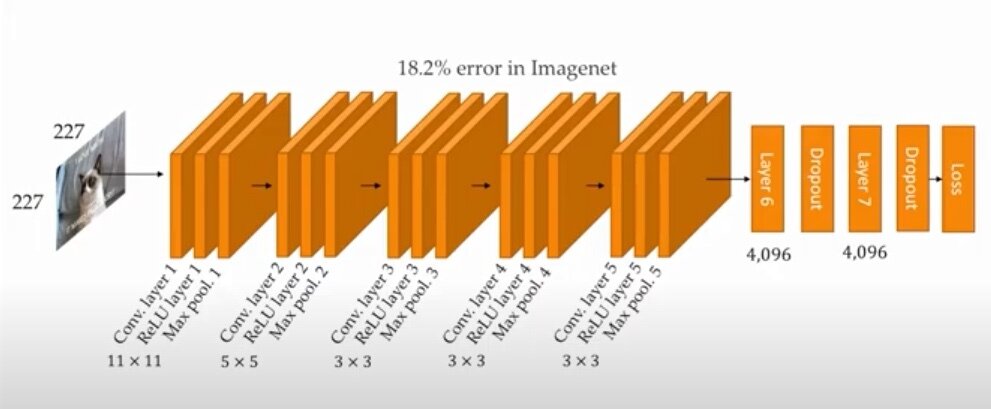
AlexNet
Deep Learning Geschichte











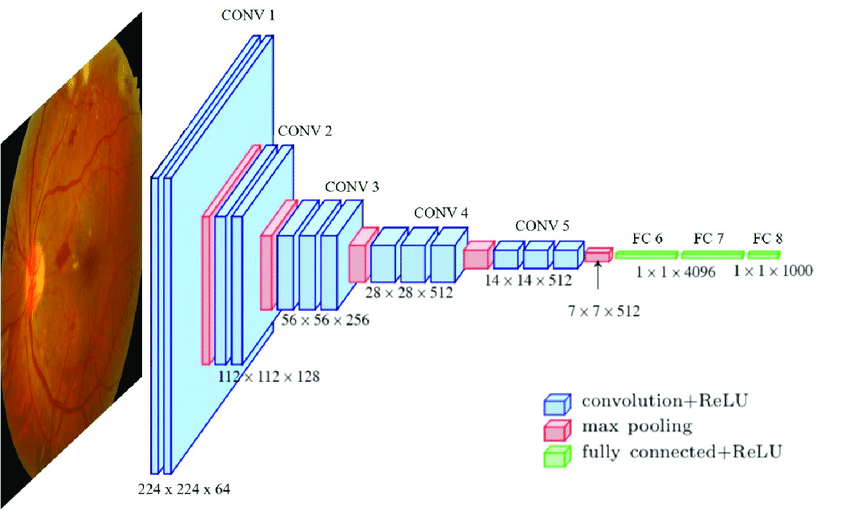
Deep Learning Geschichte












GoogleNet
Deep Learning Geschichte












Deep Learning Geschichte












Generative Adversarial Network (GAN)


Deep Learning Geschichte












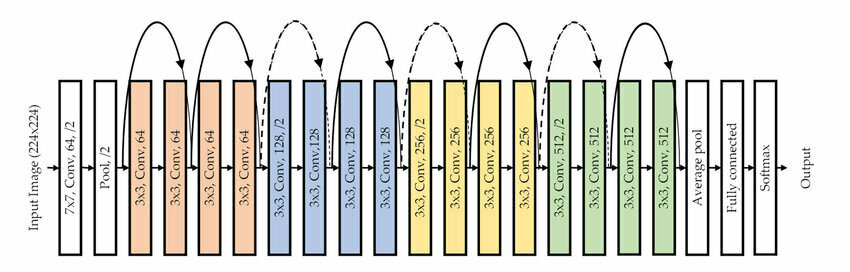
Deep Learning Geschichte













ResNet-18
Deep Learning Geschichte













Nochmal von Vorne...
Hands-On: Cifar-100 Classification
Starten Sie mit diesem Notebook
- Erstellen, trainieren und evaluieren Sie einen Classifier für den Cifar-100 Datensatz
Aufs wichtige beschränken
Hands-On: Audio Noise Reduction
Starten Sie mit diesem Notebook
- Optimieren Sie die Audio Entrauschung so, dass der Output weniger Rauschen zeigt als der Input, die Sprache aber trotzdem zu hören ist.
Squeeze the Juice ...
Hands-On: Pytorch MNIST Anomaly Detection
Betrachten Sie dieses Notebook
- Versuchen Sie, die Performance eines der Outputs zu verbessern
- Classifier
- Generator (Variational Autoencoder)
- Anomaly Detection
- Vergleichen Sie die Ergebnisse der verschiedenen Anomaly Detection methoden:
- Isolation Forest
- Mahalanobis Distanz
- VAE reconstruction error
Deep Learning
- Universeller Funktionsapproximator

Deep Learning
- Universeller Funktionsapproximator

Deep Learning
- Universeller Funktionsapproximator
- Mehr Daten, grössere Modelle
Deep Learning
- Universeller Funktionsapproximator
- Mehr Daten, grössere Modelle
- Good Practice






Deep Learning
- Universeller Funktionsapproximator
- Mehr Daten, grössere Modelle
- Good Practice
- Verstehen Sie ihr Modell!

High Performance Computing
Slurm: Umgang mit HPC Rechenclustern
Unterlagen auf Teams:
General > Class Materials > 20230710 - HowToSlurm.pdf
Ihre Meinung ist uns wichtig!
Bitte nehmen Sie sich einen Moment Zeit, um uns zu bewerten.



CAS - Deep Learning Grundlagen
By Stefan Hackstein
CAS - Deep Learning Grundlagen
- 1,005



