Decision Tree Classifiers

Suchin Gurururangan

Today

• Decision Tree Construction
• Decision Tree Prediction
• Advantages and Issues

Yesterday

• Bias-Variance Tradeoff

A brief history

  • Developed by Breiman, Friedman, Olshen, Stone in early 80’s.
  • Introduced tree-based modeling into the statistical mainstream
  • Many variants:
    • CART  --  the classic, used in scikit learn
    • CHAID
    •  C5.0
    •  ID3

Will Jane ride her bike to work today?

Day

Raining?

Temp

Humidity

Rode bike

D1

Yes

67

Low

Yes

D2

No

61

Med

Yes

D3

Yes

54

High

No

D4

No

84

High

Yes

D5

Yes

46

Low

No

D6

No

75

Med

Yes

Today

Yes

65

Low

?

Label

D7

Yes

65

High

No

D8

Yes

79

High

Yes

High level approach

  1. Pick feature to split training data samples into subsets 
  2. Measure the purity of each subset
  3. If the subset is pure, then assign classification to majority class
  4. Else repeat

Training:

Prediction:

1. Use feature combinations to figure out which subset new sample is in

2. Assign new sample to corresponding class 

Recursive Partitioning

Rain

Yes

No

Temp < 60

Temp > 60

 3 Yes / 0 No

 0 Yes / 2 No

 2 Yes / 1 No

Humidity High

1 Yes / 1 No

 2 Yes / 3 No

Humidity Low

1 Yes / 0 No

Prediction

Today

Yes

65

Low

?

Day

Raining?

Temp

Humidity

Rode bike

Rain

Yes

No

Temp < 60

Temp > 60

Humidity High

Humidity Low

1 Yes / 0 No

Yes

Question: What's the complexity of prediction on a binary decision tree?

O(log(n))
O(log(n))O(log(n))

How do we decide what attribute to split on?

Rain

Humidity

Yes

No

 3 Yes / 0 No

 2 Yes / 3 No

High

Med

Low

 1 Yes / 1 No

 2 Yes / 0 No

 2 Yes / 2 No

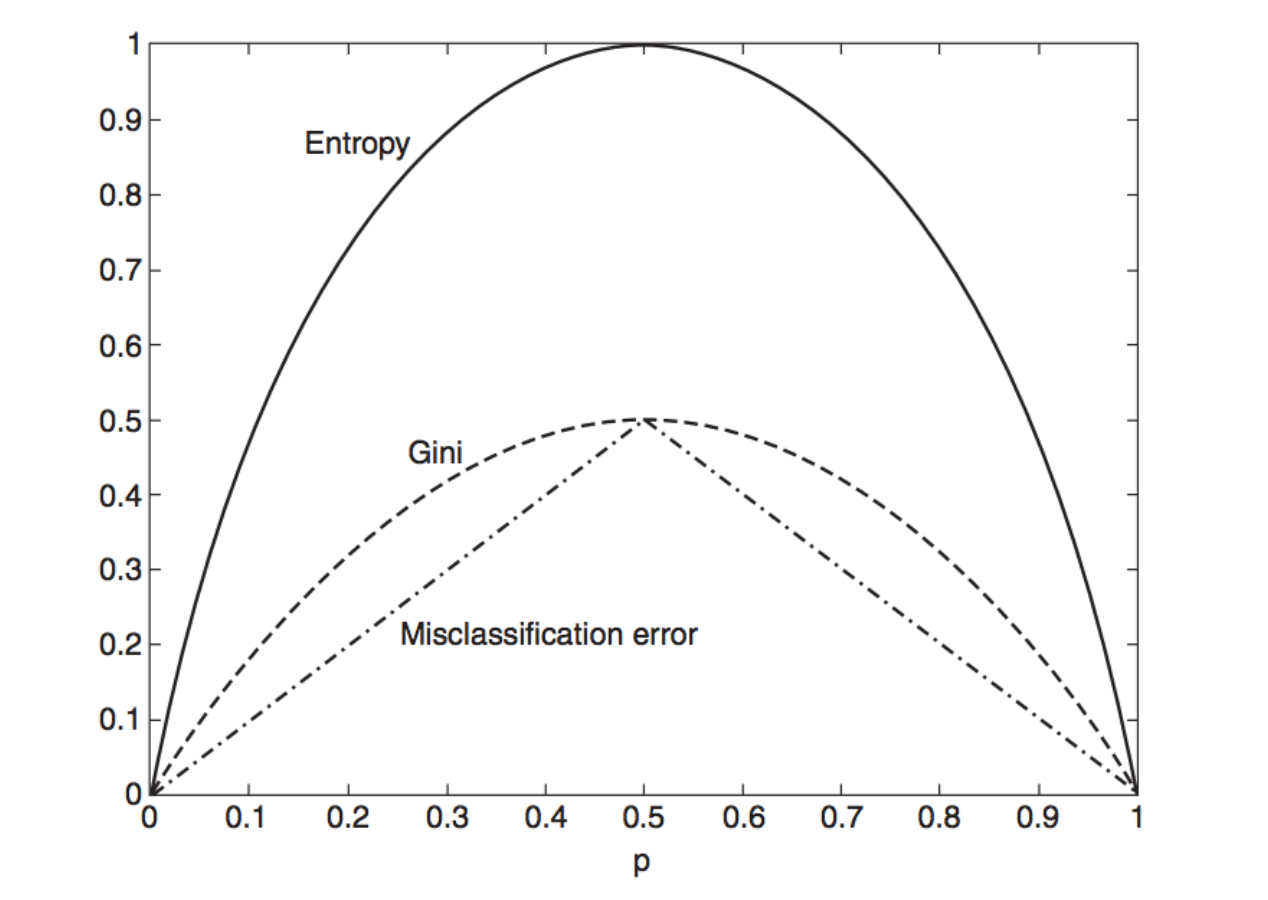
The purity (entropy, homogeneity) of the split.

 

A measure of confidence in the classification

\text{1. } Q_{left}(\theta) = {(x_i, y) | x_{ij} <= t_m}
1. Qleft(θ)=(xi,y)∣xij<=tm\text{1. } Q_{left}(\theta) = {(x_i, y) | x_{ij} <= t_m}
\text{2. } Q_{right}(\theta) = Q \setminus Q_{left}(\theta)
2. Qright(θ)=Q∖Qleft(θ)\text{2. } Q_{right}(\theta) = Q \setminus Q_{left}(\theta)
\text{3. Compute } G(Q, \theta) = H(Q_{left}(\theta)) + H(Q_{right}(\theta))
3. Compute G(Q,θ)=H(Qleft(θ))+H(Qright(θ))\text{3. Compute } G(Q, \theta) = H(Q_{left}(\theta)) + H(Q_{right}(\theta))
\text{4. Find }\theta^* = \text{argmin}_\theta G(Q, \theta)
4. Find θ∗=argminθG(Q,θ)\text{4. Find }\theta^* = \text{argmin}_\theta G(Q, \theta)
\text{ Let } \{x_1, ..., x_n\} \in X \text{ be our training data }
 Let {x1,...,xn}∈X be our training data \text{ Let } \{x_1, ..., x_n\} \in X \text{ be our training data }
\text{ and let } y \text{ be our vector of labels.}
 and let y be our vector of labels.\text{ and let } y \text{ be our vector of labels.}
\text{Feature Splitting Problem}
Feature Splitting Problem\text{Feature Splitting Problem}
\text{For each feature } x_i \text{ :}
For each feature xi :\text{For each feature } x_i \text{ :}
p_{k} = \frac{1}{N}\sum I(y_i = k)
pk=1N∑I(yi=k)p_{k} = \frac{1}{N}\sum I(y_i = k)
H = 1- \sum_k p_k^2
H=1−∑kpk2H = 1- \sum_k p_k^2
H = - \sum_k p_{k} \log(p_{k})
H=−∑kpklog(pk)H = - \sum_k p_{k} \log(p_{k})
H = 1 - \max([p_{k_1},...,p_{k_n}])
H=1−max([pk1,...,pkn])H = 1 - \max([p_{k_1},...,p_{k_n}])

Gini Impurity

Cross-Entropy Impurity

Misclassification Impurity

\text{ Let the proportion of } N \text{ labels } y_i \text{ in a subset for feature } x_i \text{ be }
 Let the proportion of N labels yi in a subset for feature xi be \text{ Let the proportion of } N \text{ labels } y_i \text{ in a subset for feature } x_i \text{ be }

Exercise

A B Label
T F Yes
T T Yes
T T Yes
T F No
T T Yes
F F No
F F No
F F No
T T No
T F No

Calculate gini, entropy, and misclassification impurities of splitting on either A or B. Which feature is best to split on?

A

T

F

4 Yes / 3 No

0 Yes / 3 No

1 - (\frac{0}{3})^2 - (\frac{3}{3})^2 = 0
1−(03)2−(33)2=01 - (\frac{0}{3})^2 - (\frac{3}{3})^2 = 0
- \frac{0}{3}log(\frac{0}{3}) - \frac{3}{3}log(\frac{3}{3}) = 0
−03log(03)−33log(33)=0 - \frac{0}{3}log(\frac{0}{3}) - \frac{3}{3}log(\frac{3}{3}) = 0
1 - max([\frac{0}{3}, \frac{3}{3}]) = 0
1−max([03,33])=01 - max([\frac{0}{3}, \frac{3}{3}]) = 0
1 - (\frac{4}{7})^2 - (\frac{3}{7})^2 = 0.49
1−(47)2−(37)2=0.491 - (\frac{4}{7})^2 - (\frac{3}{7})^2 = 0.49
T F
Gini
Cross Entropy
Misclassification
-\frac{4}{7}log(\frac{4}{7}) - \frac{3}{7}log(\frac{3}{7}) = 0.3
−47log(47)−37log(37)=0.3-\frac{4}{7}log(\frac{4}{7}) - \frac{3}{7}log(\frac{3}{7}) = 0.3
1 - max([\frac{3}{7}, \frac{4}{7}]) = 0.42
1−max([37,47])=0.421 - max([\frac{3}{7}, \frac{4}{7}]) = 0.42

B

T

F

3 Yes / 1 No

1 Yes / 5 No

1 - (\frac{1}{6})^2 - (\frac{5}{6})^2 = 0.28
1−(16)2−(56)2=0.281 - (\frac{1}{6})^2 - (\frac{5}{6})^2 = 0.28
- \frac{1}{6}log(\frac{1}{6}) - \frac{5}{6}log(\frac{5}{6}) = 0.2
−16log(16)−56log(56)=0.2 - \frac{1}{6}log(\frac{1}{6}) - \frac{5}{6}log(\frac{5}{6}) = 0.2
1 - max([\frac{1}{6}, \frac{5}{6}]) = 0.17
1−max([16,56])=0.171 - max([\frac{1}{6}, \frac{5}{6}]) = 0.17
1 - (\frac{3}{4})^2 - (\frac{1}{4})^2 = 0.38
1−(34)2−(14)2=0.381 - (\frac{3}{4})^2 - (\frac{1}{4})^2 = 0.38
T F
Gini
Cross Entropy
Misclassification
-\frac{3}{4}log(\frac{3}{4}) - \frac{1}{4}log(\frac{1}{4}) = 0.24
−34log(34)−14log(14)=0.24-\frac{3}{4}log(\frac{3}{4}) - \frac{1}{4}log(\frac{1}{4}) = 0.24
1 - max([\frac{3}{4}, \frac{1}{4}]) = 0.25
1−max([34,14])=0.251 - max([\frac{3}{4}, \frac{1}{4}]) = 0.25
A B
Gini 0.49 0.68
Cross Entropy 0.3 0.44
Misclassification 0.42 0.42

Total Impurities

Split on feature A with Gini/Cross Entropy Impurity

Randomly choose with Misclassification Impurity

What if we chose day as our feature split? 

Decision trees tend to overfit the training data.

Day

D1

D2

D3

D4

D5

 1 Yes / 0 No

 1 Yes / 0 No

 1 Yes / 0 No

 1 Yes / 0 No

 1 Yes / 0 No

Next class:

  • How do we avoid overfitting?
  • How do we avoid unnecessary leaves and branches?
  • Cost complexity pruning
  • Cross-validation

deck

By Suchin Gururangan

Made with Slides.com

deck

  • 816

More from Suchin Gururangan