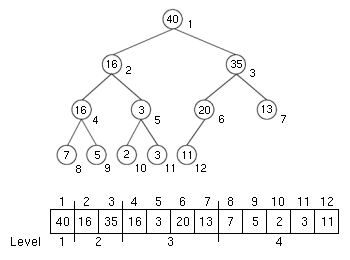
Heaps

👉 for Heap definition

👇refresher on Binary Trees

@swyx || swyx.io

Binary Trees

• Trees where each node only has up to 2 children
• "Complete" tree = every level filled; last level filled from left to right
• "Full" tree = No node has 1 child.
• "Perfect" = Full + Complete

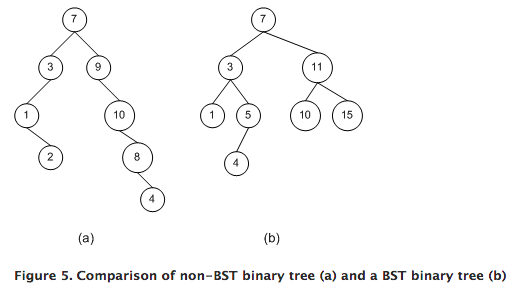
Binary Search Trees

• All left descendents <= node value < all right descendents

Heap Definition

• Complete Binary Trees
• A type of priority queue
• Satisfies the heap property, either a Min-Heap or Max-Heap.
• In a Max-Heap, if P is a parent node of C
  • then P >= C
  • compare vs BSTs:
  • No idea if C1 < C2
• Top node is max/min value
• There are non-binary heaps

👉 for Heap methods

👇 vs other Data Structures

BSTs

• Insert: O(lg N) avg
• Contains: O (lg N) avg
• Remove: O(lg N) avg
• getMin: O(lg N)
• in/post/preordered traversal

Heaps

• Insert: O(lg N) avg
• Contains: O (lg N) avg
• Remove: O(lg N) avg
• getMin: O(1)
• ordered traversal not possible

PQueues (Linked List)

• Insert: O(N)
• Contains: O(N) avg
• Remove: O(1) avg
• getMin: O(1)
• basically insertion sort

Heaps

• Insert: O(lg N) avg
• Contains: O (lg N) avg
• Remove: O(lg N) avg
• getMin: O(1)

What else?

I can't do the full comparisons justice

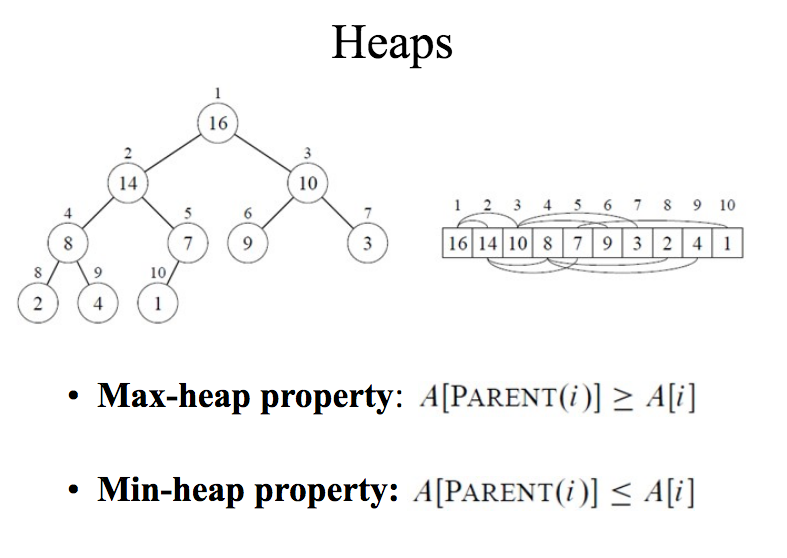
Key Methods

(and their Complexity)

• peek: O(1)
• remove: O(lg N)
• insert: O(lg N)
• Internal Methods:
  • Swap(i, j): O(1)
  • SiftDown(i): O(lg N) - used by remove
  • SiftUp(i): O(lg N) - used by insert

👉 Practice Time!

👇 pseudocode for methods

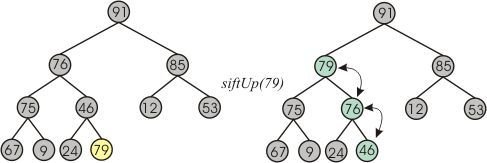
Sift-Up

Example:

• Given a valid Max-Heap, insert 79 at the end (of the array/heap)
• Compare to 79's parent
• Swap up if 79 > 79's parent
• repeat until 79 < parent
• You now have a new, valid Max-Heap with 79 in it

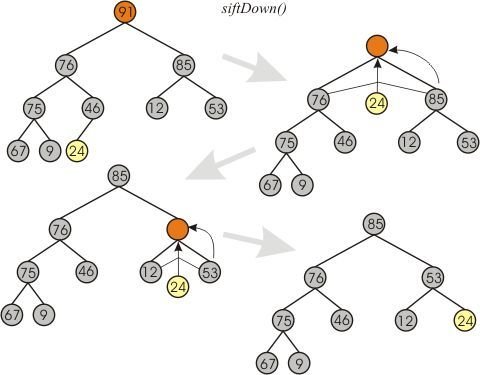
Sift-Down

Example:

• Given a valid Max-Heap, remove the max (91) and pull the last node (24) into the root
• Now the Heap is invalid, 24 is less than 76 or 85
• Swap down 24 with the bigger of the two children (85, then 53)
• Repeat until you have a valid Max-Heap again, with 91 popped off.

Review: Why Use A Heap

• O(1) Retrieval of Max or Min
• O(1) Space complexity (same as Trees)
• O(lg N) Insertion/Removal

Used in these Algorithms:

• Heap Sort (great big O properties)
  • no O(n^2) worst case eg QuickSort
  • O(1) space compared to MergeSort O(n)
• Continuous Median
• (if sparse) Dijkstra's Algorithm

👉 for End of Slides/More Resources

👇Heap Sort and Continuous Median

Heap Sort

Given an unsorted array, produce a sorted array using heap sort

First try doing it on top of a complete Heap Sort implementation like here:

https://repl.it/@swyx/Heaps-Basic-Solution

Then practice writing from scratch

Solution

1. Subdivide into unsorted (A) and an empty (B)
2. Put A into a Max-Heap
3. While A is not empty, pop off the root of A and unshift it into B
4. B is the sorted array

Notes

1. Sorting done in-place
2. Video

Continuous Median

Write a class that can support the following two functionalities: 1) the continuous insertion of numbers and 2) the instant (O(1) time) retrieval of the median of the numbers that have been inserted thus far.

Solution

1. Class has a maxHeap, a minHeap, and a median
2. insert by comparing with max of minHeap or min of maxHeap
   1. then rebalance
   2. then update median
3. rebalance by comparing lengths
   1. e.g. minHeap > maxHeap
   2. x = minHeap.remove()
   3. maxHeap.insert(x)
4. update median
   1. if equal length, get average
   2. if unbalanced, peek longer

Dijkstra's Algo

• Find the shortest path between a and b.
  • It picks the unvisited vertex with the lowest distance
  • calculates the distance through it to each unvisited neighbor
  • updates the neighbor's distance if smaller.
• Use a pQ to keep track of vertex with lowest distance
  • LList if not sparse
  • Heap if E << V² / logV
    • Especially Fibonacci Heap
• see wiki for pseudocode

Other Notes

• Here
• DecreaseKey is tricky
  • either write it
  • or keep a hash table