Graphs of Geodesically-Convex Sets
Loose Ends, and SO(3) without SDPs
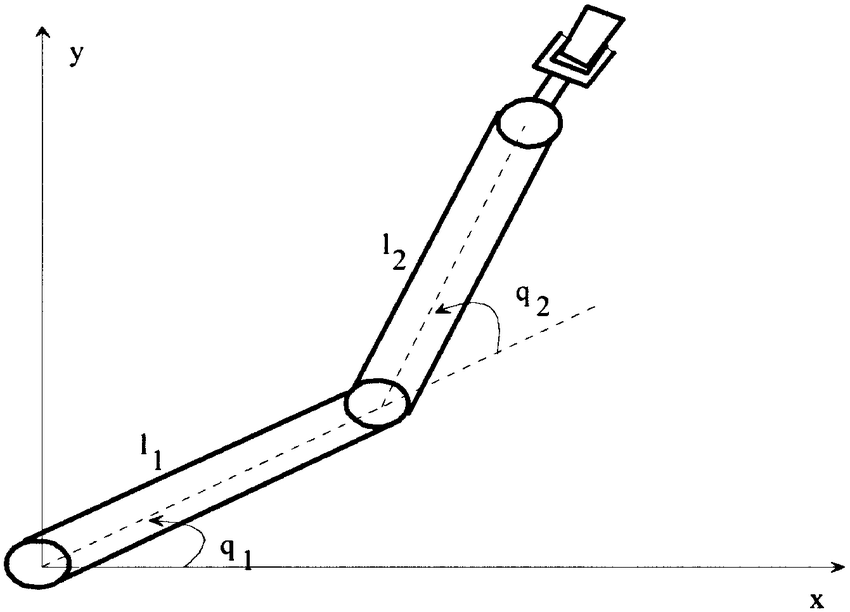
Robot Configuration Spaces as Smooth Manifolds
Robust Combined Adaptive and Variable Structure Adaptive Control of Robot Manipulators, Yu
(No joint limits)
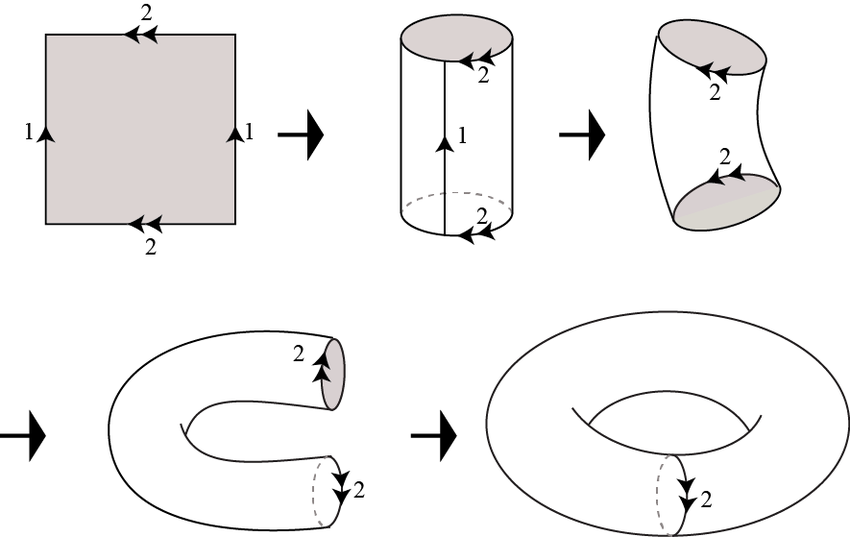
Survey of Graph Embeddings into Compact Surfaces, Potoczak
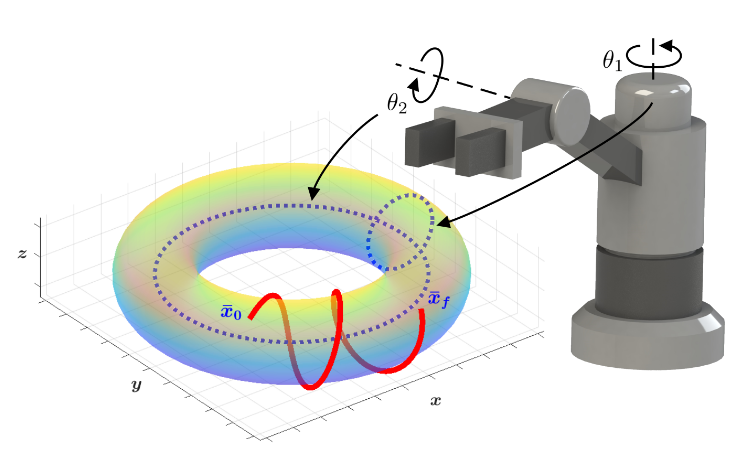
Trajectory Optimization on Manifolds: A Theoretically-Guaranteed Embedded Sequential Convex Programming Approach, Bonalli et. al.
Geodesics: Shortest Paths
For a curve \(\gamma\) connecting two points \(p=\gamma(0),q=\gamma(1)\) on a manifold, its arc length is
\[\int_0^1||\dot\gamma(t)||\,\mathrm{d}t\]
Geodesics on Surfaces by Variational Calculus, Villanueva
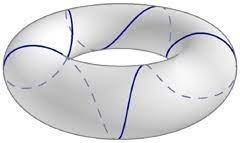
The Curvature and Geodesics of the Torus, Irons
This yields a distance metric
\[d(p,q)=\inf\{L(\gamma)\,|\,\gamma\in\mathcal{C}^{1}_{\operatorname{pw}}([0,1],\mathcal{M}),\\\gamma(0)=p,\gamma(1)=q\}\]
A geodesic is a (locally) length-minimizing curve.
Convex Sets
A set \(X\subseteq\mathbb{R}^n\) is convex if \(\forall p,q\in X\), the line connecting \(p\) and \(q\) is contained in \(X\)
Geodesically Convex Sets
A set \(X\subseteq\mathcal{M}\) is strongly geodesically convex if \(\forall p,q\in X\), there is a unique length-minimizing geodesic (w.r.t. \(\mathcal{M}\)) connecting \(p\) and \(q\), which is completely contained in \(X\).
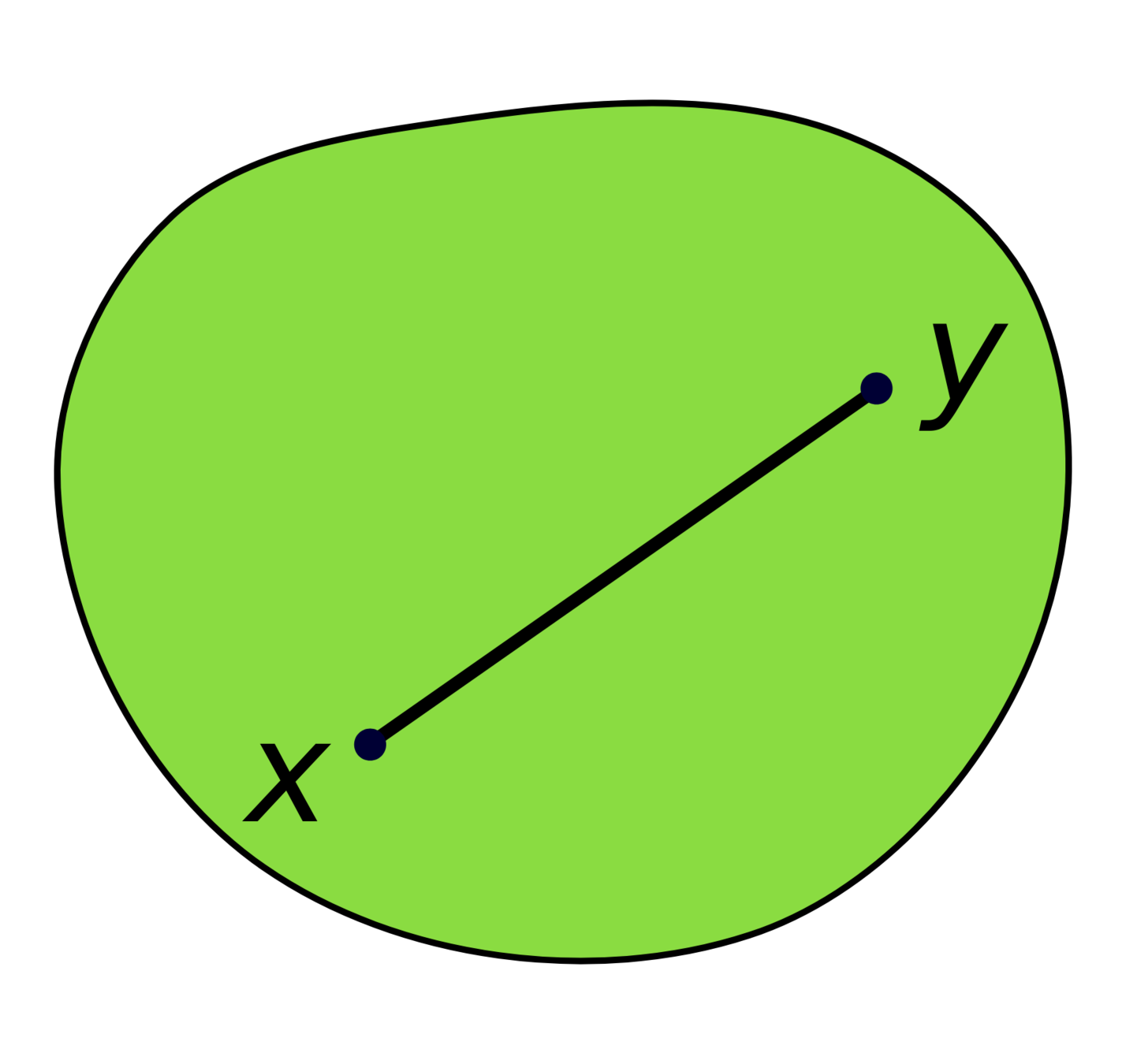
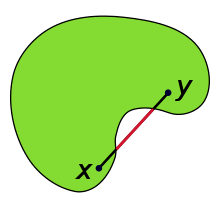
Convex Set, Wikipedia
Convex Functions
A function \(f:X\to\mathbb{R}\) is convex if for any \(x,y\in X\) and \(\lambda\in[0,1]\), we have
\[f(\lambda x+(1-\lambda)y)\le\]
\[\lambda f(x)+(1-\lambda) f(y)\]
Geodesically Convex Functions
A function \(f:\mathcal{M}\to\mathbb{R}\) is geodesically convex if for any \(x,y\in \mathcal{M}\) and any geodesic \(\gamma:[0,1]\to\mathcal{M}\) such that \(\gamma(0)=x\) and \(\gamma(1)=y\), \(f\circ\gamma\) is convex
Convex Functions
Geodesically Convex Functions

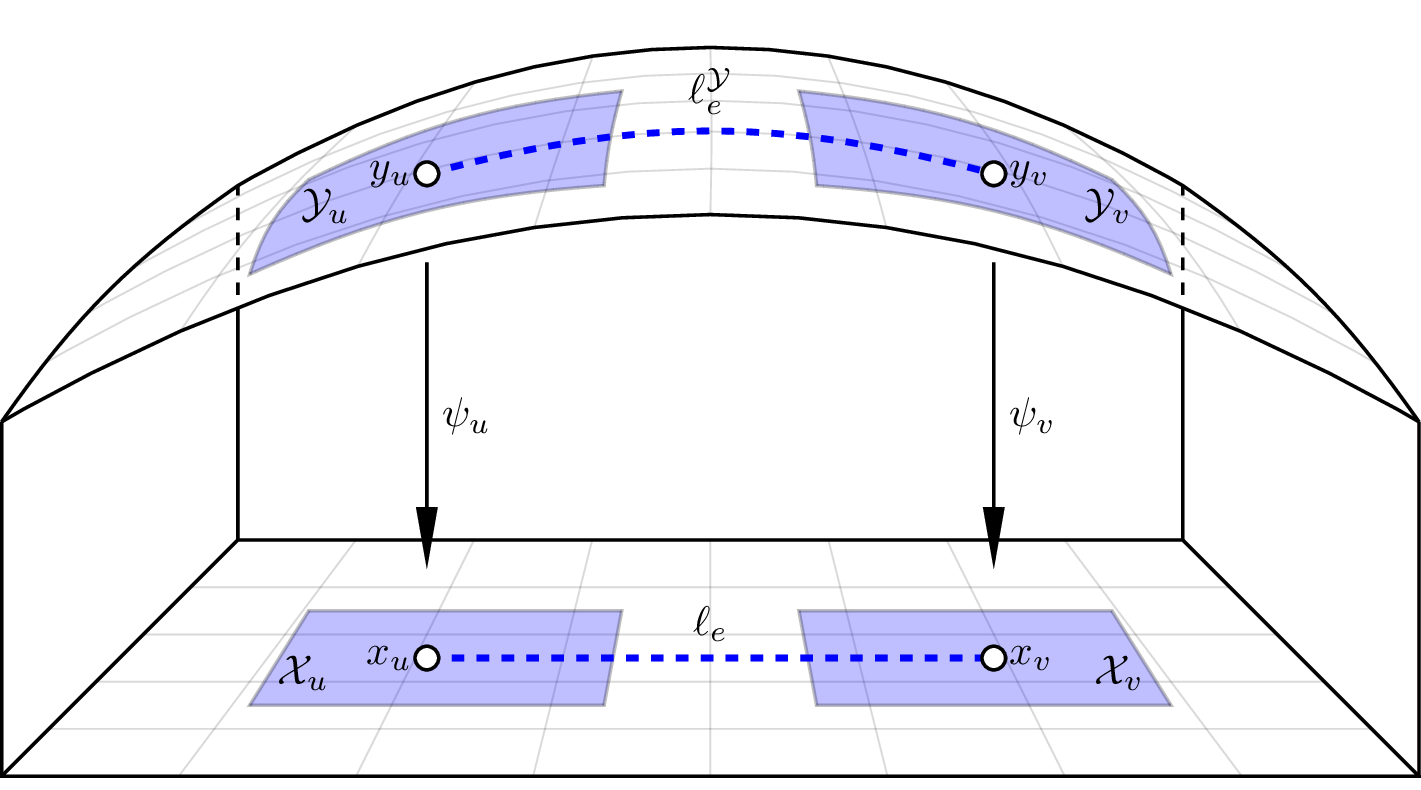
A Graph of Geodesically Convex Sets (GGCS)
A directed graph \(G=(V,E)\)
- For each vertex \(v\in V\), there is a strongly geodesically convex manifold \(\mathcal{Y}_v\)
- For each edge \(e=(u,v)\in E\), there is a cost function \(\ell_e^\mathcal{Y}:\mathcal{Y}_u\times\mathcal{Y}_v\to\mathbb{R}\)
- \(\ell_e^\mathcal{Y}\) must be geodesically convex on \(\mathcal{Y}_u\times\mathcal{Y}_v\)
Transforming Back to a GCS
When is it Convex?
Have to consider the curvature of the manifold.
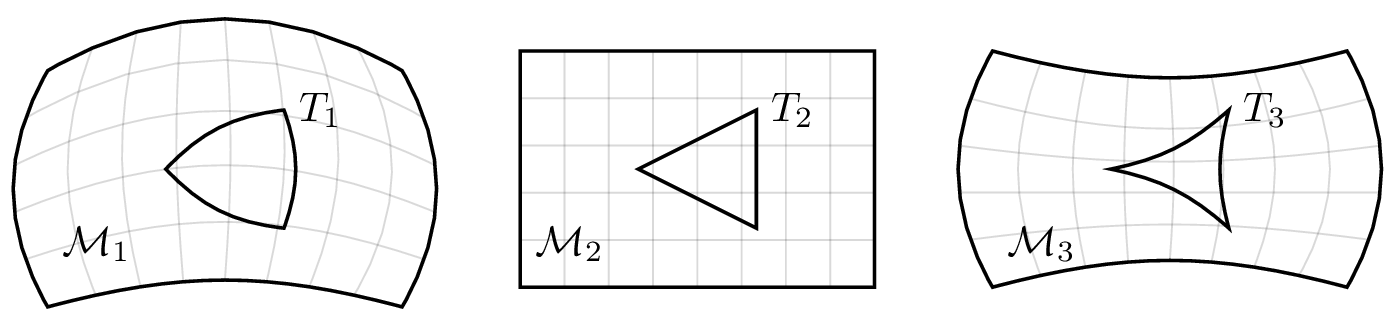
Positive curvature
E.g. \(S^n,\operatorname{SO}(3),\operatorname{SE}(3)\)
Negative curvature
E.g. Saddle, PSD Cone \(\vphantom{S^n}\)
Zero curvature
E.g. \(\mathbb R^n, \mathbb T^n\)


Zero-Curvature is Still Useful
- All 1-dimensional manifolds
- Continuous revolute joints
- \(\operatorname{SO}(2)\), \(\operatorname{SE}(2)\)
- Products of flat manifolds
Fetch Robot Configuration
Space: \(\operatorname{SE}(2)\times \mathbb{T}^3\times \mathbb{R}^7\)

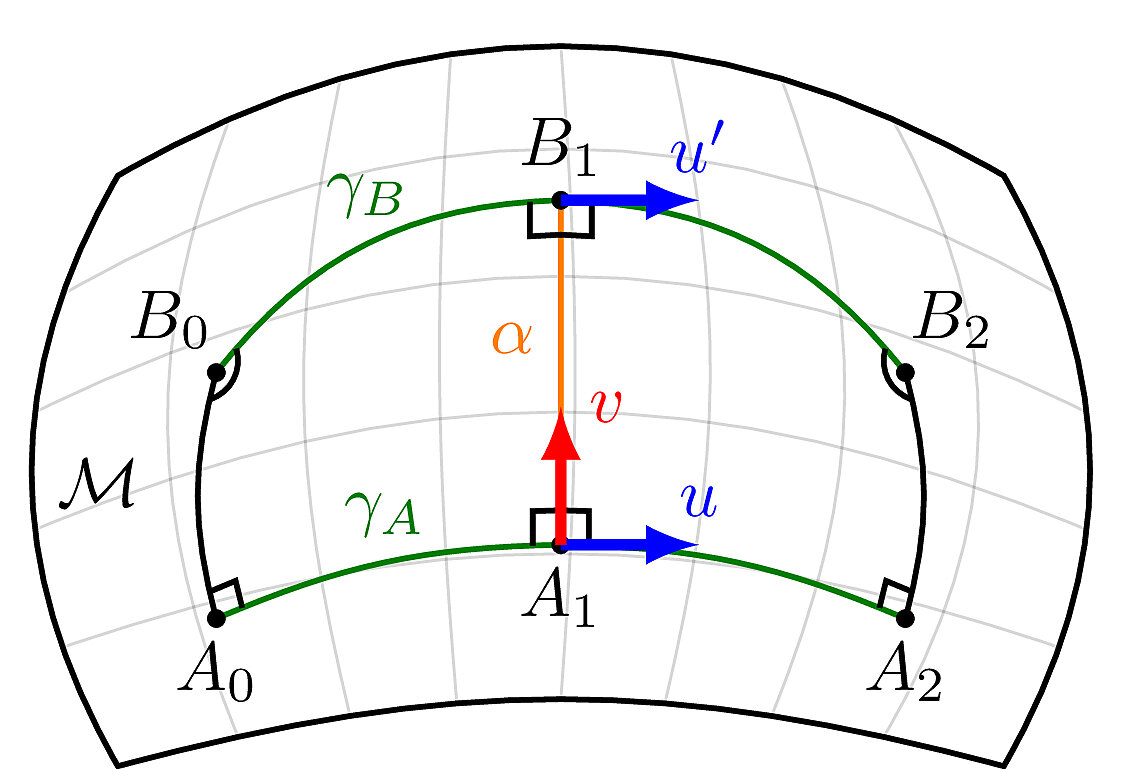
Why is Positive Curvature Bad?

Planning on PL Approximations
Path Planning on Manifolds using Randomized Higher-Dimensional Continuation, Porta and Jaillet
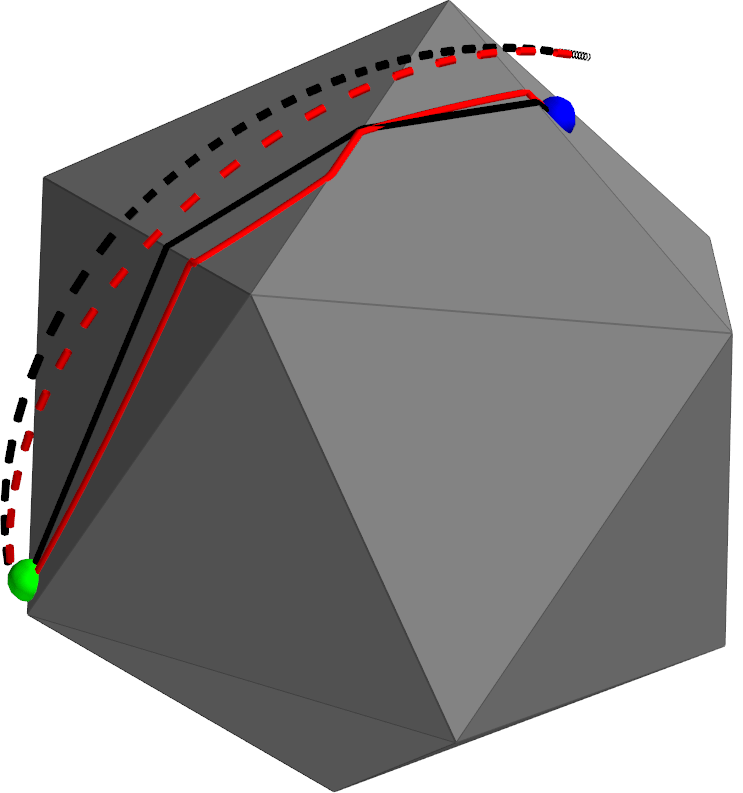


Planning on PL Approximations
Black: Shortest path on PL approximation
Red: Shortest path on sphere
Rough Bounds on Approximation Error
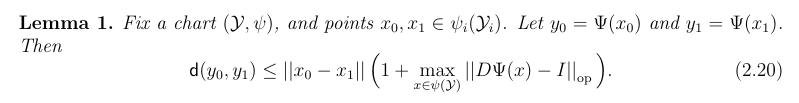
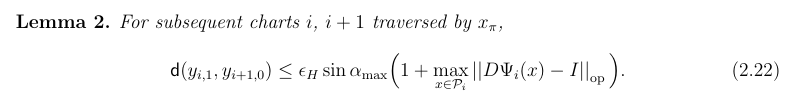
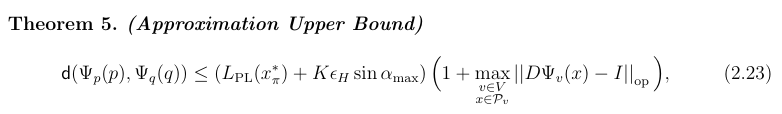
Intuition: How much does the Jacobian of the chart vary?
Intuition: The amount we can "slip" along the boundary also depends on the Hausdorff distance \(\epsilon_H\) between the manifold and its triangulation, as well as the angle \(\alpha_{\operatorname{max}}\) between adjacent charts.
Intuition: The error grows additively with the number of sets traversed in the optimal path.
Focusing on SO(3)/SE(3)
Recall that \(\operatorname{SE}(3)\) is just \(\operatorname{SO}(3)\times\mathbb R^3\)
Three representations for \(\operatorname{SO}(3)\):
- Euler angles (\(S^1\times S^1\times S^1\))
- 27 sets, 702 edges (fully connected)
- Axis-angle (\(S^2\times S^1\))
- 60 sets, 660 edges
- Quaternions (\(S^3\))
- 27 sets and 390 edges or 64 sets and 2240 edges
\(S^1\) is flat (no approximation needed)
Numerical Comparison
Randomly sample \(n\) start and goal pairs, plan between them with each approximation.
Compute the true distance, and explore the error distribution.
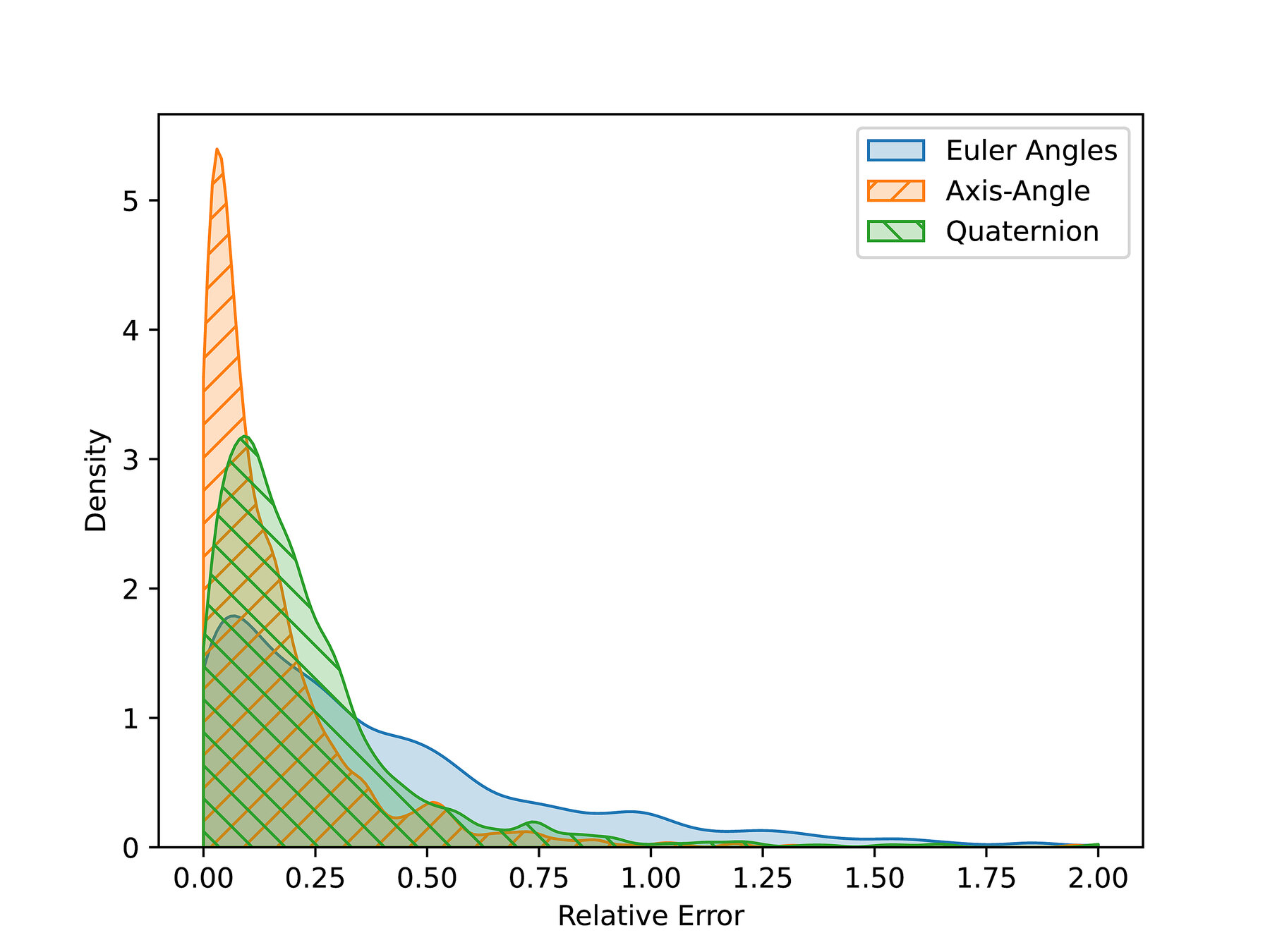
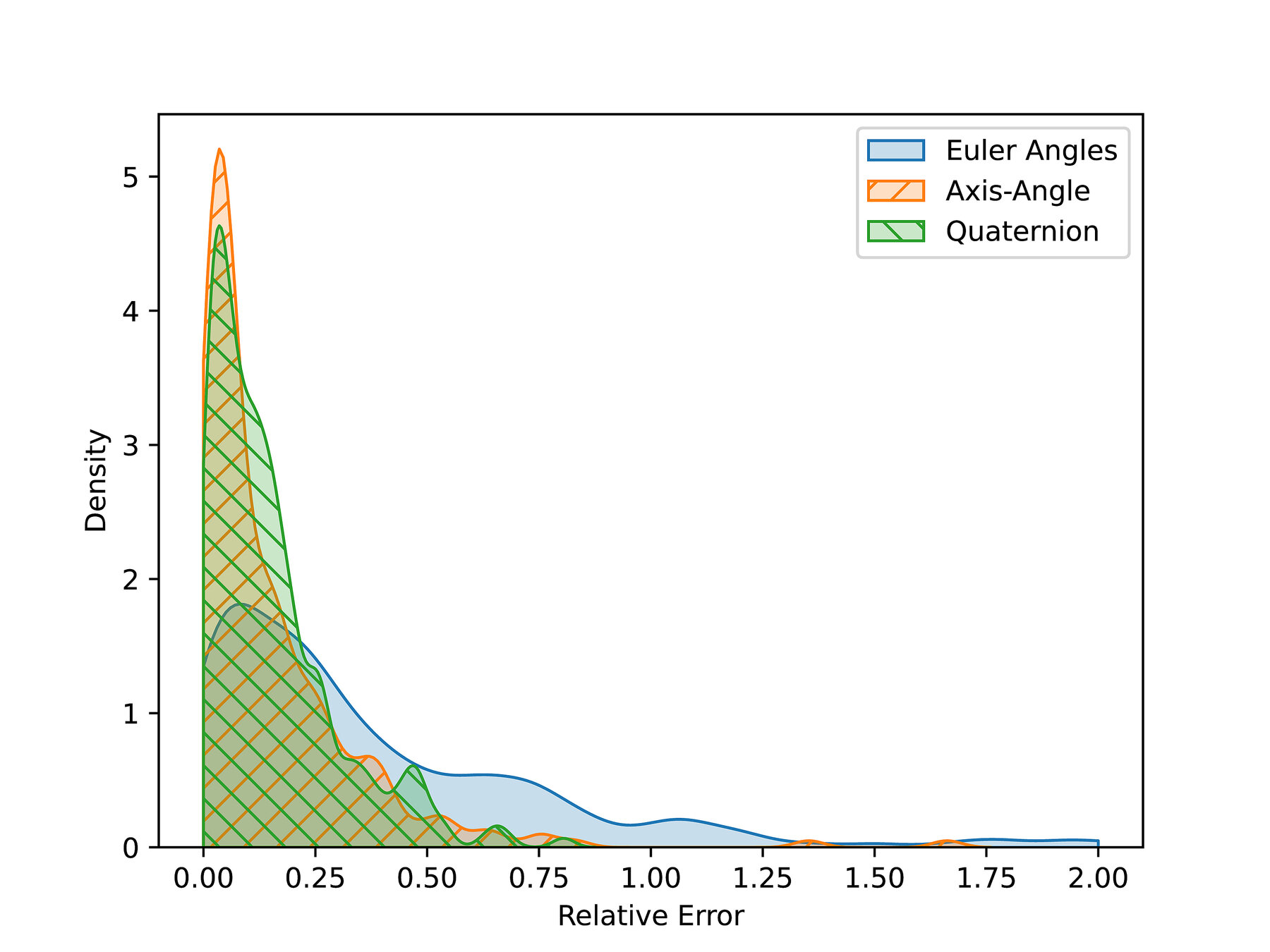
Note: two possible representations in axis-angle and quaternion, so we plan twice. Euler angles are stranger, so we ignore.
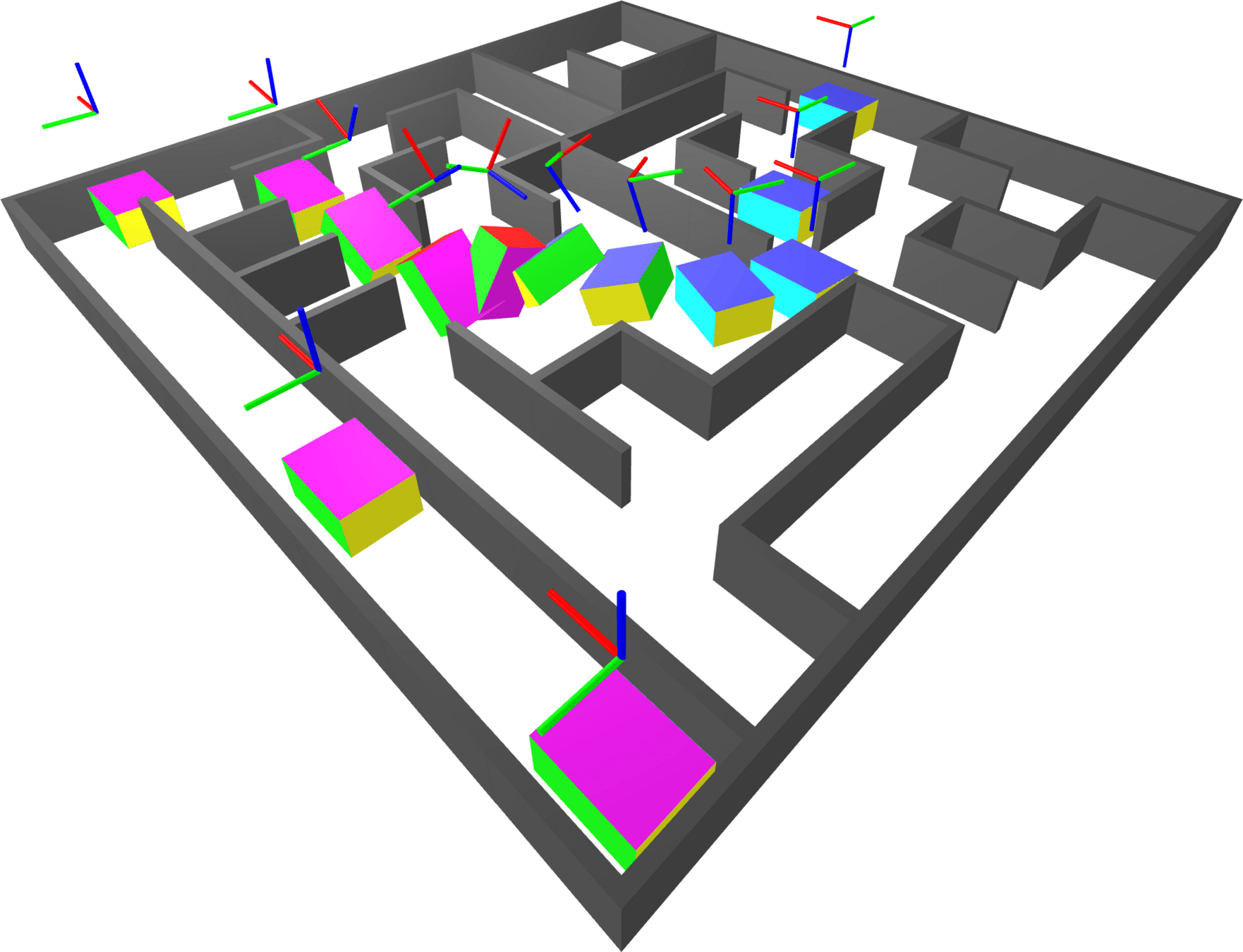
SE(3) Maze
Consider a block moving freely in 3D through a 2D maze.
Generate collision free regions with IRIS-NP. (Have to use Euler angles.)
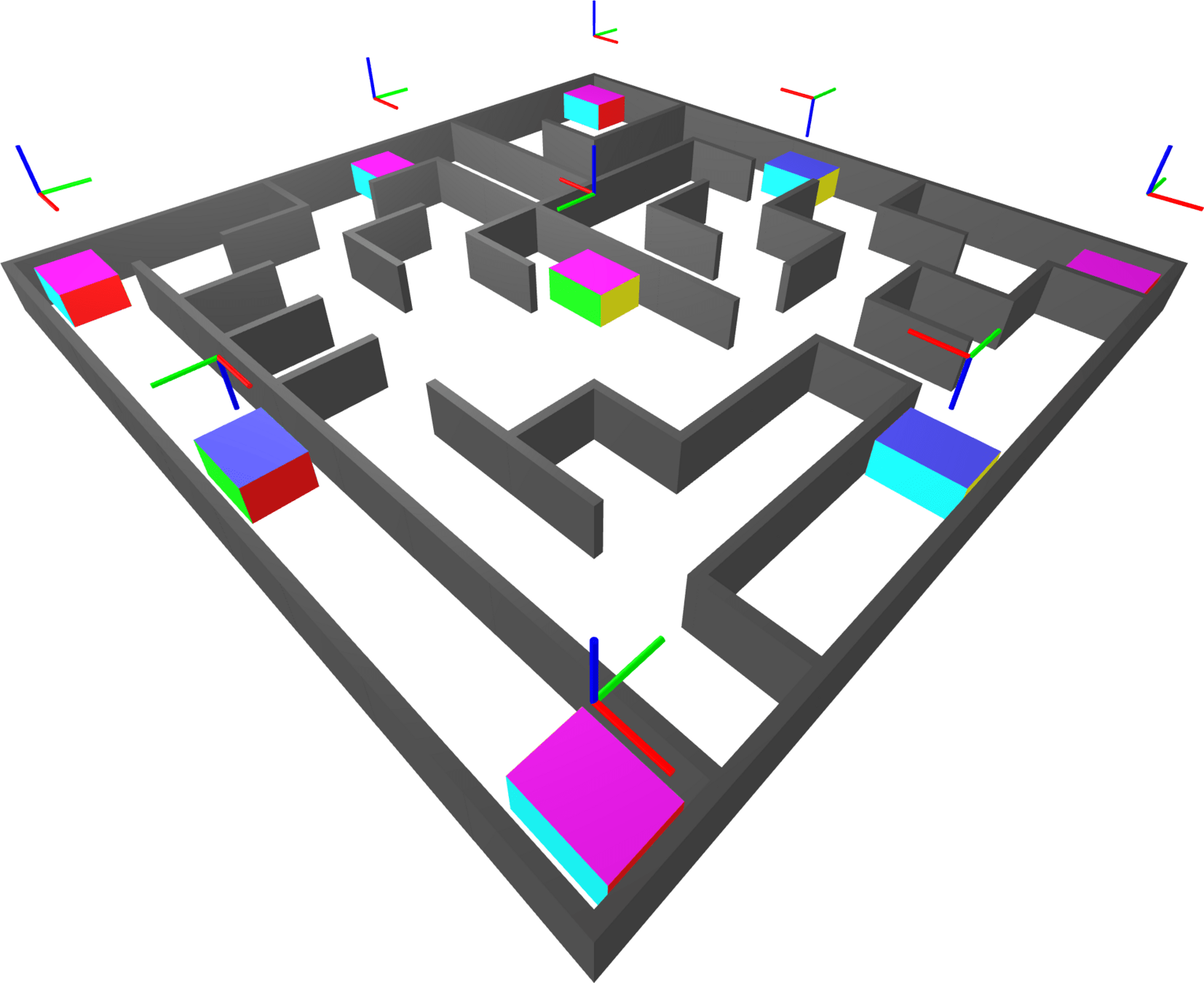
More Setup Details
Making the graph:
- Create a grid-like roadmap
- Cover subset of edges with IRIS regions to connect key poses
200 sets, 4744 edges
- Good engineering
- Loose tolerance for relaxation (\(\sim 10^3\))
- Use L1-norm for convex relaxation (still use L2-norm for the convex restriction)
Tricks to deal with the bigger graph:
Shortest Paths in the Maze
Sample path between a start/goal pair.
The large gap in the center gives room for the block to reorient itself.
Statistics across All Pairs
GCS average runtime: 354.98 seconds
GCS* average runtime: 46.71 seconds
GCS* is ~7 times faster, and produces paths that are only 4.4% longer than GCS on average.
Takeaway: For large collision-free kinematic motion planning problems, use GCS*
What's Next?
- Shruti's talk
- SO(3) representations are non-unique, but maybe we can get around that with auxiliary vertices and edges.
- Can interpret this as a configuration-space symmetry
- I'll be talking more about this next week
RLG Group Meeting Short Talk 11/15/24
By tcohn
RLG Group Meeting Short Talk 11/15/24
- 239



