The Quotient Topology and Object Symmetries

Thomas Cohn

February 24, 2023
Motivation:
Symmetries in Planning
Global Planning for Contact-Rich Manipulation via Local Smoothing of Quasi-dynamic Contact Models, Pang et. al.
Motivation:
Symmetries in Planning
Motivation:
Symmetries in Planning
Idea: Describe the Configuration Space up to Symmetry
Benefits:
- Can take advantage of symmetries to find shorter plans
- Smaller configuration space -- can find plans faster
Mathematical language: quotient spaces
Intuition: Quotients as Gluing


Topology, Munkres
Equivalence Relations
An Equivalence Relation \(\sim\) on a set \(X\) is a subset of \(X\times X\) s.t.
- \(x\sim x\) (Reflexivity)
- \(x\sim y\Rightarrow y\sim x\) (Symmetry)
- \(x\sim y,y\sim z\Rightarrow x\sim z\) (Transitivity)
An Equivalence Relation \(\sim\) on a set \(X\) is a subset of \(X\times X\) s.t.
- \(x\sim x\) (Reflexivity)
- \(x\sim y\Rightarrow y\sim x\) (Symmetry)
- \(x\sim y,y\sim z\Rightarrow x\sim z\) (Transitivity)
The equivalence class of an element \(x\in X\) is
\[[x]:=\{y\in X:x\sim y\}\]
Quotient Space
Given an equivalence relation \(\sim\) on \(X\), we can consider the set of equivalence classes \[X/\!\sim\;:=\{[x]:x\in X\}\]
We have the projection map \[\pi:X\to X/\!\sim\quad x\mapsto[x]\]
If \(X\) has certain properties, does \(X/\!\sim\)?
Answer: Sometimes
Quotient Topology
If \(X\) is a topological space, we can use \(\pi\) to define the quotient topology on \(X/\!\sim\), where \(Y\subseteq X/\!\sim\) is an open set iff \(\pi^{-1}(Y)\) is open in \(X\).
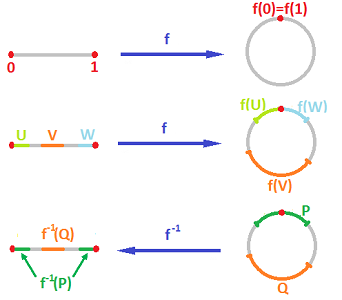
https://calculus123.com/wiki/Quotients
Intuition: Quotients as Gluing


Topology, Munkres
Groups and Group Actions
Example of a group: rotations in \(\mathbb{R}^3\), called \(\operatorname{SO}(3)\)
- Has an identity element
- Every rotation has an inverse
- Can compose two rotations and get a new one
Example of a group action: rotations applied to points in \(\mathbb{R}^3\)
- Must be compatible with the group operation
A group action yields an equivalence relation
- \(x\sim y\) if there is a rotation \(R\) such that \(R(x)=y\)
The Quotient Manifold Theorem
If \(\mathcal{M}\) is a manifold, and \(G\) is a group that acts on \(\mathcal{M}\), then* \(\mathcal{M}/\!\sim\), also written as \(\mathcal{M}/G\), is a manifold.
*Assuming \(G\) satisfies various technical properties. See Introduction to Smooth Manifolds, Lee, Chapter 21, for details.
The Riemannian Case
Under certain further conditions (which are satisfied by the symmetry groups of rigid bodies), \(\mathcal{M}/G\) gets a Riemannian metric from \(\mathcal{M}\).
Furthermore, the distance function takes the following form: \[d([x],[y])=\inf\{d(x,y):x\in[x],y\in[y]\}\]
For a finite group \(G\), this is just a minimum of finitely many entries.
Infinite symmetry groups still have nice properties?
RLG Group Meeting Short Talk 2/24/23
By tcohn
RLG Group Meeting Short Talk 2/24/23
- 255



