Constrained Bimanual Planning with Analytic Inverse Kinematics

Thomas Cohn, Seiji Shaw, Max Simchowitz, Russ Tedrake

September 29 2023
Outline
- Background: Constrained Planning
- Background: Analytic IK
- Reparametrizing the Constraint Manifold
- Planning with the Reparametrization
- Next Steps
Part 1
Constrained Planning
Configuration-Space Planning
https://github.com/ethz-asl/amr_visualisations
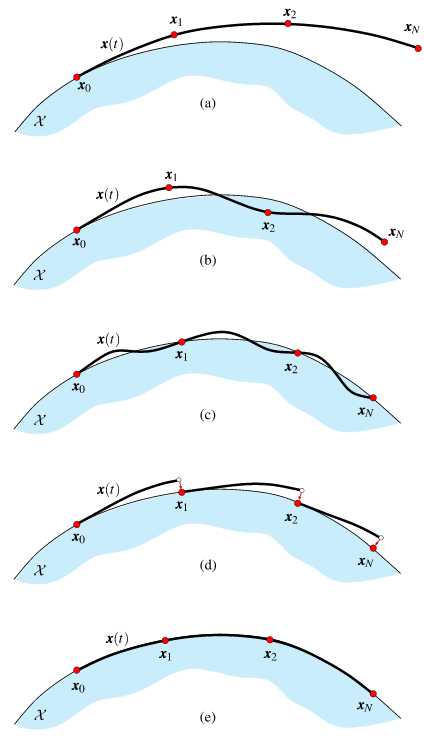
Task-Space Constraints
Learning the Metric of Task Constraint Manifolds for Constrained Motion Planning, Zha et. al.
Existing Approaches
Trajectory Optimization

Trajectory Optimization On Manifolds with
Applications to \(SO(3)\) and \(\mathbb{R}^3 \times S^2\), Watterson et. al.
Trajectory Optimization on Manifolds: A
Theoretically-Guaranteed Embedded Sequential
Convex Programming Approach, Bonalli et. al.
Direct Collocation Methods for Trajectory
Optimization in Constrained Robotic Systems, Bordabla et. al.
Existing Approaches
Sampling-Based Planning
Sampling-Based Methods for Motion Planning with Constraints, Kingston et. al.
Part 2
Analytic Inverse Kinematics
Inverse Kinematics
https://thewanderingtech.blogspot.com/2009/06/educational-flash-application-on.html


Global Inverse Kinematics via
Mixed-Integer Convex Optimization, Dai et. al.
https://www.youtube.com/watch?v=c87OyAZDS54
Analytic Inverse Kinematics
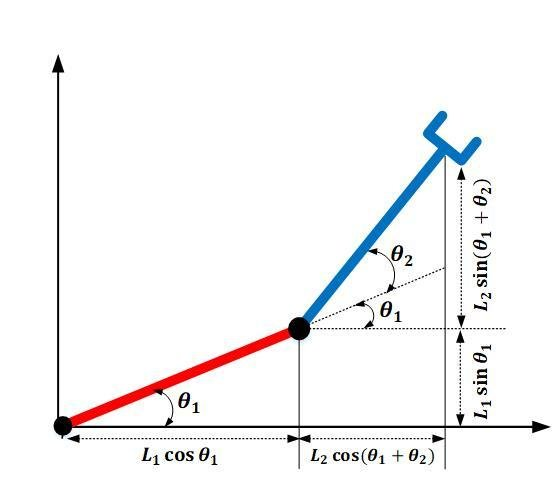
Robot Arm Free Cartesian Space Analysis for Heuristic Path Planning Enhancement, Raheem et. al.
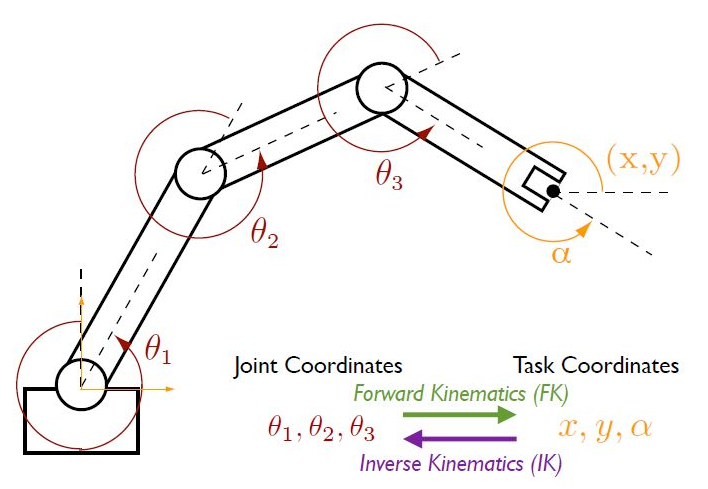
https://disigns.wordpress.com/portfolio/solving-inverse-kinematics/
Analytic Inverse Kinematics





IKFast
Part 3
Reparametrizing the Constraint Manifold
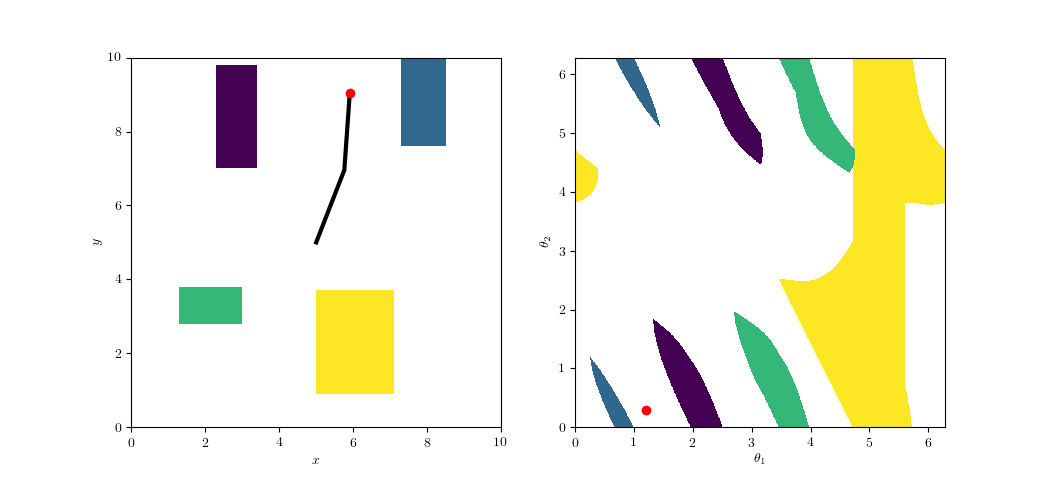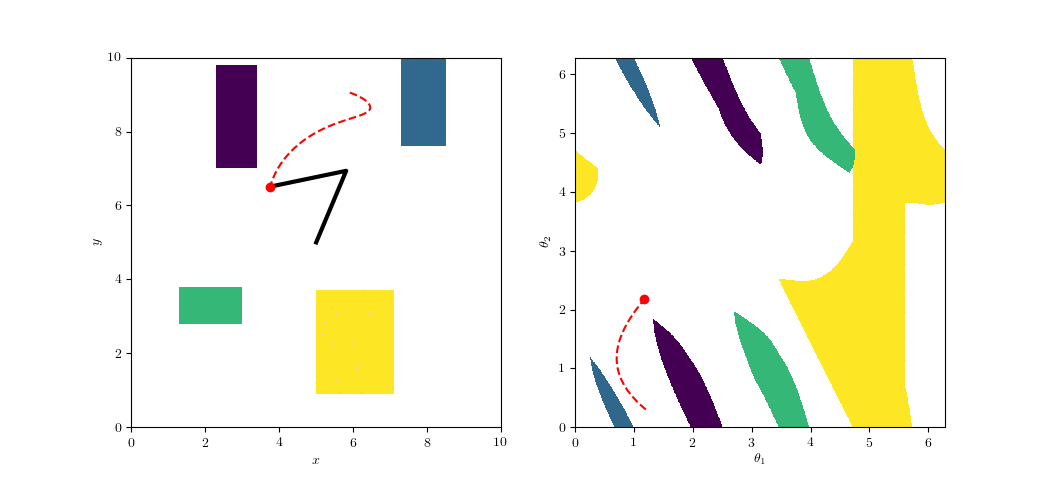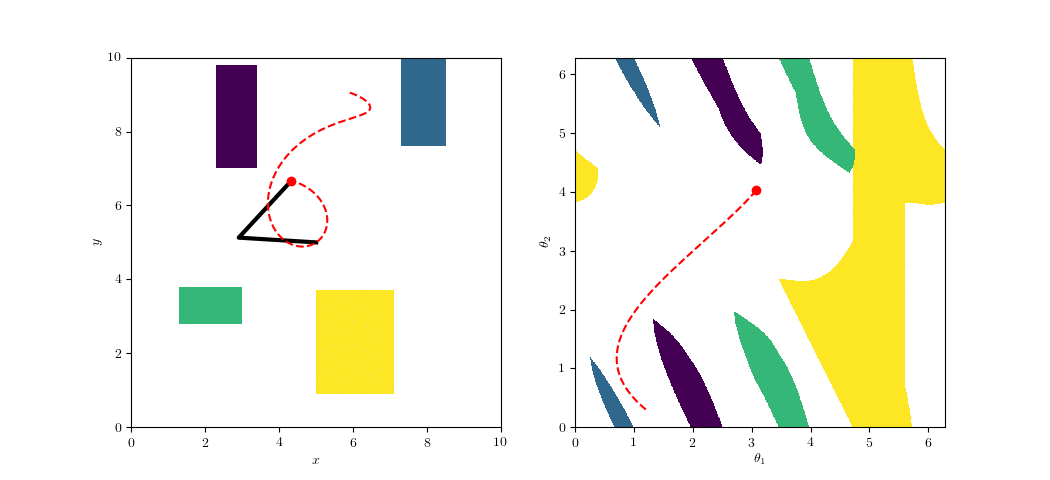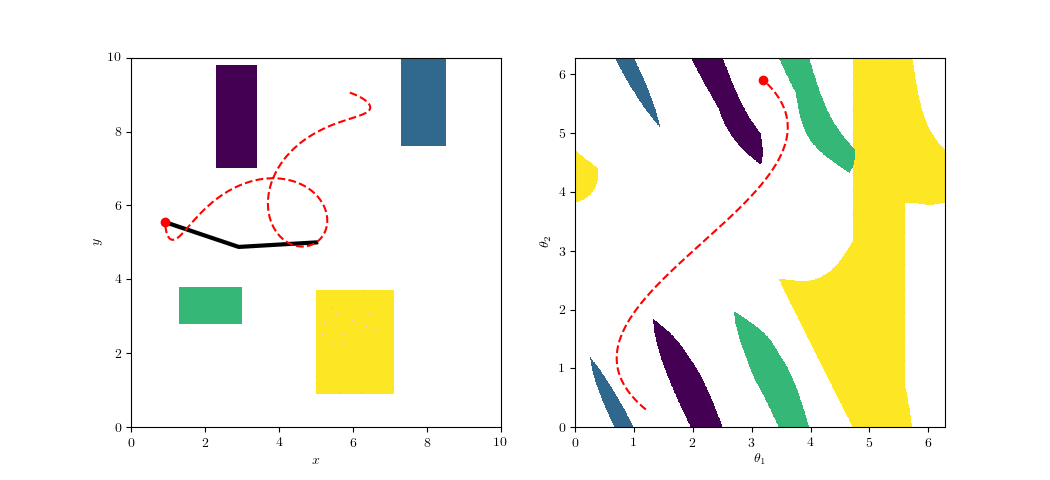
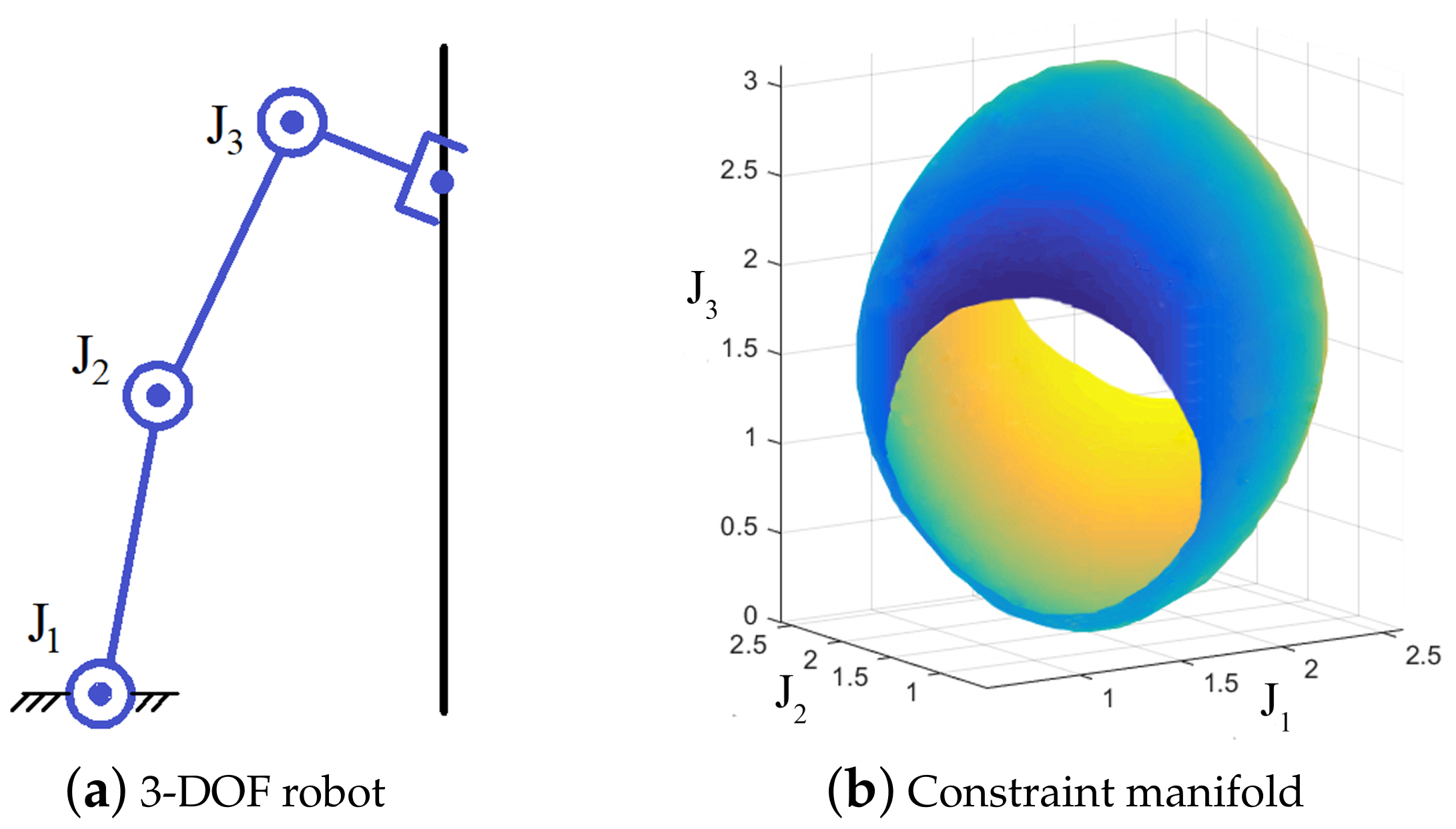
System Setup
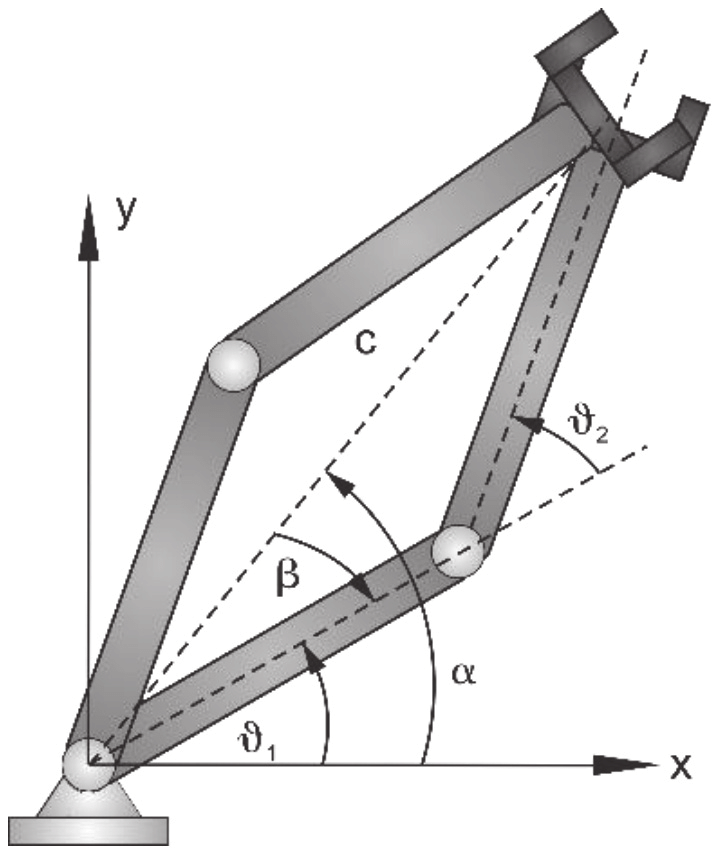
Problem: FK is Not Injective
Kinematics of Serial Manipulators, Virgala et. al.

Self Motion
Making IK a Bijection
- Fix a global configuration
- Treat the redundancy parameter as an argument
- Restrict the domain and range to avoid singularities, etc.
Topology of Kinematics
- Configuration space \(\mathcal{Q}\)
- End-effector space \(\mathcal{X}\)
- Forward kinematics \(f:\mathcal{Q}\to\mathcal{X}\)
- Regular Point: \(q\in\mathcal{Q}\) s.t. \(Df(q)\) is full rank
- Critical Point: \(q\in\mathcal{Q}\) s.t. \(Df(q)\) is singular
- Regular Value: \(x\in\mathcal{X}\) s.t. \(\forall q\in f^{-1}(x)\), \(Df(q)\) is full rank
- Critical Value: \(x\in\mathcal{X}\) s.t. \(\forall q\in f^{-1}(x)\), \(Df(q)\) is singular
- Coregular Value: \(x\in\mathcal{X}\) s.t. \(\exists q_1,q_2\in f^{-1}(x)\) s.t. \(Df(q_1)\) is full rank and \(Df(q_2)\) is singular
Topology of Kinematics (cont'd)
- \(\mathcal{W}\)-Sheet: A connected set of regular and coregular values. Their boundaries are called Critical Value Manifolds.
- \(\mathcal{C}\)-Bundle: A connected set of regular points. Their boundaries are called Coregular Surfaces.
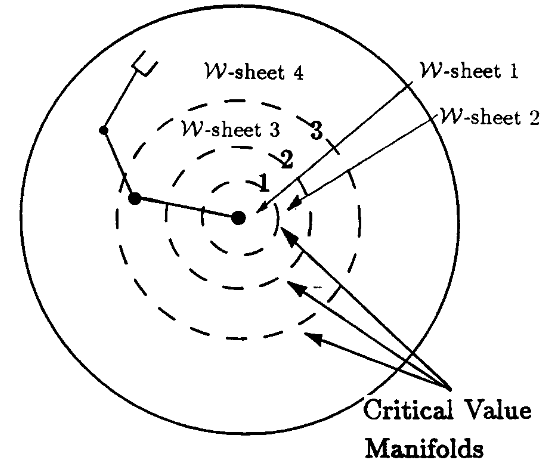
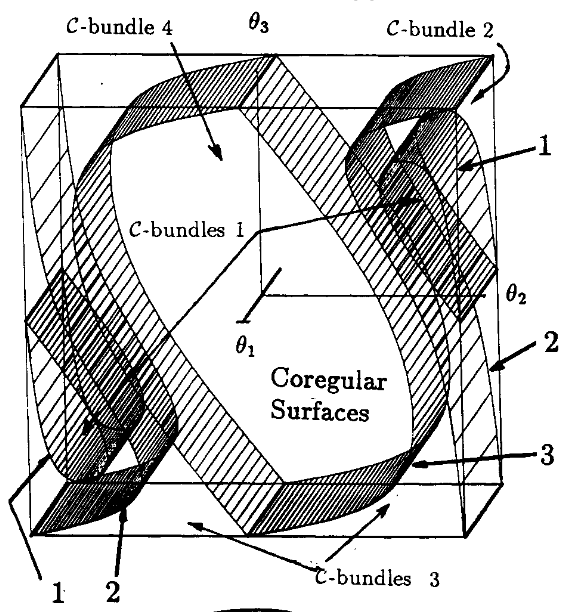
On the inverse kinematics of redundant manipulators: characterization of the self-motion manifolds, Burdick
Making IK a Bijection
- Fix a global configuration
- Treat the redundancy parameter as an argument
- Restrict the domain and range to avoid singularities, etc.
- End effector must stay within a single \(\mathcal{W}\)-sheet
- Joints must stay within a single \(\mathcal{C}\)-bundle
Our Parametrization in Practice
Part 4
Planning with the Reparametrization
Sampling-Based Planning
Easy! Just draw samples in the parametrized space
C.f. Atlas-BiRRT (from OMPL)
Trajectory Optimization
C.f. Baseline
But We're the Robot Locomotion Group...
So let's do GCS
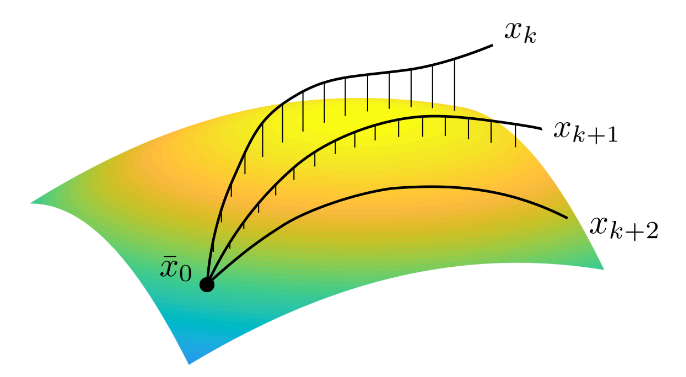
Constrained IRIS
Grow an IRIS region in the parametrized space
Multiple sources of hyperplanes
- IK Mapping Domain (\(\arccos(w)\) where \(w\not\in[-1,1]\))
- Subordinate arm joint limit violations
- Reachability violations
- Collisions
Harder optimization landscape -- need many more counterexample searches
IRIS Random Walk
GCS Planning
- All planning done in the parametrized space
- Use arc length in parametrized space as the objective
- Self-motion manifolds?
- In our experience, don't need GGCS -- just cut the configuration space
- If the joints or self-motions can wrap around, we can use a flat metric.
Varying the Grasp Distance
- Can treat the entries of the end-effector transform (e.g. grasp distance) as free variables for IRIS
- Fix the transform at plan time
Part 5
Next Steps
" 'Harder Better
Faster Stronger'
-Daft Punk "
-Tommy Cohn
More Ideas
- Post-processing GCS trajectories with PGD
- Improve trajectories while maintaining guarantees
- Planning across \(\mathcal{C}\)-bundles and \(\mathcal{W}\)-sheets
- When can/can't we avoid singularities?
- Manipulating articulated objects in the environment
- Tools, doors, drawers, rubix cubes?
- Extend to more general kinematic structures
- Leverage a formulation of IK as an eigenvalue problem
Constrained Bimanual Planning with Analytic Inverse Kinematics

Thomas Cohn, Seiji Shaw, Max Simchowitz, Russ Tedrake

September 29 2023
RLG Group Meeting Long Talk 9/29/23
By tcohn
RLG Group Meeting Long Talk 9/29/23
- 237



