Dictionaries, Hash Tables and Sets
Telerik Academy Alpha

 

DSA

 Table of contents

  • Dictionaries

  • Hash Tables

  • Dictionary Class

  • HashSet and SortedSet

  • Advanced Data Collections

Dictionaries

What is Dictionary

  • A dictionary is an indexed collection that allows values to be found by user-defined keys










 

  • ​Definition - Dictionary<int, string>
     
  • Also known as map or associative array
Key Value
1 Sofia
2 Plovdiv
3 Burgas
4 Ruse

Why using Dictionaries

Very fast searching by key

O(1)

 

 The Dictionary (Map) ADT

  • Operations:
    • Add(key, value)
    • FindByKey(key) 
    • Delete(key)
       
  • Can be implemented in several ways
    • List, array, hash table, balanced tree

Hash Tables

HashTable

The most efficient implementation of Dictionary

What is HashTable

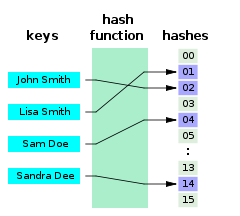
 Hash Tables Efficiency

 

  • Add / Find / Delete take just a few primitive operations
    • Speed does not depend on the size of the hash-table
      • Amortized complexity \( O(1) \)
    • Example: finding an element in a hash-table with 1 000 000 elements takes just a few steps
      • Finding an element in array of 1 000 000 elements takes average 500 000 steps

 Hash Tables

  • A hash table is an array that holds a set of (key, value) pairs
  • The process of mapping a key to a position in a table is called hashing
  • A hash table has m slots, indexed from 0 to m-1
  • A hash function h(k) maps keys to positions:
    • \( h: k \rightarrow 0 ... (m-1) \)
  • For any value k in the key range and some hash function h we have h(k) = p and 0 ≤ p < m

 Example of hashing


A hash table of length 10 uses open addressing with hash function h(k)=k mod 10, and linear probing. After inserting 6 values into an empty hash table, the table is as shown below. The numbers are: 46, 34, 42, 23, 52, 33

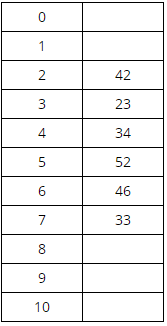
42 mod 10 = 2

34 mod 10 = 4

33 mod 10 = 3

 Hash Tables

  • Perfect hashing function (PHF)
    • \( h(k) \) : one-to-one mapping of each key k to an integer in the range \( [0, m-1] \)
    • The PHF maps each key to a distinct integer within some manageable range
  • Finding a perfect hashing function is in most cases impossible
  • More realistically, hash function \( h(k) \) that maps most of the keys onto unique integers, but not all

 Collisions in Hash Tables

  • A collision is a situation when different keys have the same hash value
    • ( h(k1) = h(k2) ) for ( k1 != k2 )



       

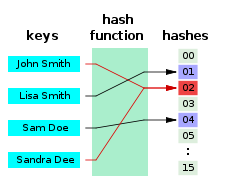
 NB: When the number of collisions is sufficiently small, the   hash tables work quite well (fast)

Resolving Collisions

  • Strategies

    • Chaining in a list
    • Using the neighboring slots (linear probing)
    • Re-hashing (second hash function)

Chaining in a list:

Dictionaries in C#

Dictionary<TKey, TValue>

Type of the key

Type of the value

Task

Create collection containing information about a city's temperature

 Dictionary

  • Implements the ADT dictionary as hash table
    • The size is dynamically increased as needed
    • Contains a collection of key-value pairs
    • Collisions are resolved by chaining
    • Elements have almost random order
      • Ordered by the hash code of the key
  • Dictionary relies on
    • Object.Equals() – for comparing the keys
    • Object.GetHashCode() – for calculating the hash codes of the keys

 Dictionary

  • Major operations:
    • Add(TKey,TValue) – adds an element with the specified key and value
    • Remove(TKey) – removes the element by key
      this[] – get / add / replace of element by key
    • Clear() – removes all elements
    • Count – returns the number of elements
    • Keys – returns a collection of the keys
    • Values – returns a collection of the values

 Dictionary

  • Major operations:
    • ContainsKey(TKey) – checks whether the dictionary contains the given key
    • ContainsValue(TValue) – checks whether the dictionary contains the given value
      • Warning: slow operation – \( O(n) \)
         
    • TryGetValue(TKey, out TValue)
      • If the key is found, returns it in the TValue
        Otherwise, returns false

Task

1. Update info for each city to contain population and country

  2. Update population for a particular city                                   

Task

Override Equals and GetHashCode methods

 

(Try the performance when they return the same value for each item)

 Dictionary Demo - Student Grades

Sorted Dictionaries in C#

SortedDictionary

Dictionary with items ordered by key

 SortedDictionary

  • SortedDictionary implements the ADT "dictionary" as self-balancing search tree​
    • Traversing the tree returns the elements in increasing order
    • Add / Find / Delete perform ( log2(n) ) operations
       
  • Use SortedDictionary when you need the elements sorted by key
    • Otherwise, use Dictionary – it has better performance

Task

User SortedDictionary to count the time each word appears in:

 

 string text = "a text some text just some text";

Note: Write on paper

 SortedDictionary Demo - Word Count

 Quizlet

  1. Which one is faster in Dictionary - searching by value or by key?
  2. HashTable - add/find/delete operations- do or do not depend on the size?
  3. What is a collision? 
  4. ContainsValue - is or is not fast operation?
  5. Which element will be this one:




     
  6. Equals method is used for ...? GetHashCode() is used for ...?
  7. Dictionaries resolve collision by ....?
  8. How would those elements be ordered:



 

var dictionary = new Dictionary<int, string>();
 
dictionary.Add(1, "one");
dictionary.Add(2, "two");
dictionary.Add(3, "three");

var element = dictionary.ElementAt(1);
var dictionary = new SortedDictionary<int, string>();

dictionary.Add(2, "c");            
dictionary.Add(1, "a");           
dictionary.Add(3, "b");

Sets

Set

Keeps items with no duplicates

Bag

Keeps items with duplicates

 Set and Bag ADTs

  • Operations:
    • Add(element)
    • Contains(element) → true / false
    • Delete(element)
    • Union(set) / Intersect(set)
       
  • Sets can be implemented in several ways
    • List, array, hash table, balanced tree

HashSet

Set implementation by HashTable

 HashSet

  • Elements are in no particular order
     
  • All major operations are fast:
    • Add(element) – appends an element to the set
      • Does nothing if the element already exists
    • Remove(element) – removes given element
    • Count – returns the number of elements
    • UnionWith(set) / IntersectWith(set) – performs union / intersection with another set

 HashSet Demo

SortedSet

HashSet with elements sorted in increasing order

 SortedSet

  • SortedSet implements ADT set by balanced search tree (red-black tree)

Advanced Data Structures

 Wintellect Power Collections

  • Wintellect Power Collections is powerful open-source data structure library
  • Installing Power Collections in Visual Studio
    • Use NuGet package manager

 Power Collections Classes

  • Bag<T>
    • A bag (multi-set) based on hash-table
    • Unordered collection (with duplicates)
    • Add / Find / Remove work in time \( O(1) \)
    • T should provide Equals() and GetHashCode()
  • OrderedBag<T>
    • A bag (multi-set) based on balanced search tree
    • Add / Find / Remove work in time \( O(log(N)) \)
    • T should implement IComparable<T>

 Power Collections Classes

  • Set<T>
    • A set based on hash-table 
    • Add / Find / Remove work in time \( O(1) \)
    • Like .NET’s HashSet<T>
  • OrderedSet<T>
    • A set based on balanced search tree (red-black)
    • Add / Find / Remove work in time \( O(log(N)) \)
    • Like .NET’s SortedSet<T>
    • Provides fast .Range(from, to) operation

 Power Collections Classes

  • MultiDictionary<TKey,TValue>
    • A dictionary (map) implemented by hash-table
    • Allows duplicates (configurable)
    • Add / Find / Remove work in time \( O(1) \)
    • Like Dictionary<TKey,List<TValue>>
  • OrderedDictionary<TKey,TValue>
  • OrderedMultiDictionary<TKey,TValue>
    • A dictionary based on balanced search tree
    • Add / Find / Remove work in time \( O(log(N)) \)
    • Provides fast .Range(from,to) operation

 Power Collections Classes

  • Deque<T>
    • Double-ended queue (deque)
  • BigList<T>
    • Editable sequence of indexed items
    • Like List<T> but provides
      • Fast Insert / Delete operations (at any position)
      • Fast Copy / Concat / Sub-range operations
    • Implemented by the data structure "Rope"
      • Special kind of balanced binary tree

PriorityQueue

A queue which elements have priority associated with it

 Priority Queue

  • Why using PriorityQueue
    • Find the item with the highest priority
       
  • Operations
    • Enqueue (T element)
    • Deque() → T
       
  • There is no built-in priority queue in .NET
    • See the data structure "binary heap"
    • Can be implemented also by OrderedBag

 Priority Queue Implementation

class PriorityQueue<T> where T : IComparable<T>
{
   private OrderedBag<T> queue;
   public int Count
   {
      get { return this.queue.Count; }
   }
   public PriorityQueue()
   {
      this.queue = new OrderedBag<T>();
   }
   public void Enqueue(T element)
   {
      this.queue.Add(element);
   }
   public T Dequeue()
   {
      return this.queue.RemoveFirst();
   }
}

 Quizlet

  1. What is the difference between Set and Bag?
  2. Set or Bag has Union and Intersect methods?
  3. What is the Difference between SortedSet (.Net) and OrderedSet(PowerCollection)? 
  4. Which collections do support Range(from, to)?
  5. What would be the order of:





     
  6. Which collections use Rope structure?
  7. PriorityQueue can be implemented easily with ...?
var firstSet = new SortedSet<string>(new string[] { "Alabama", "Washington", "Colorado", "New York" });
var secondSet = new SortedSet<string>(new string[] { "New York", "Alaska", "Alabama" });
 
var union = new SortedSet<string>(firstSet);
union.UnionWith(secondSet);

Questions

[C# DSA] Dictionaries, Hash Tables and Sets

By telerikacademy

Made with Slides.com

[C# DSA] Dictionaries, Hash Tables and Sets

  • 1,529

More from telerikacademy