Sorting and Searching Algorithms
Telerik Academy Alpha

 

DSA

 Table of contents

What is a sorting algorithm?

 What is a sorting algorithm?

  • Sorting algorithm
    • An algorithm that puts elements of a list in a certain order
  • More formally:
    • The output is in some order
    • The output is a permutation of the input
  • Efficient sorting is important for
    • Producing human-readable output
    • Optimizing the use of other algorithms
  • Sorting presents many important techniques

 Sorting algorithms animation

https://www.toptal.com/developers/sorting-algorithms/

https://visualgo.net/en/sorting

 Classification

  • Sorting algorithms are often classified by

    • Computational complexity

      • worst, average and best behavior

    • Memory usage

    • Recursive or non-recursive

    • Stability

    • Whether or not they are a comparison sort

    • General method

      • insertion, exchange (bubble sort and quicksort), selection (heapsort), merging, serial or parallel…

 Stability

  • Stable sorting algorithms

    • Maintain the relative order of records with equal values

  • If two items compare as equal, then their relative order will be preserved

    • When sorting only part of the data is examined when determining the sort order

Sorting algorithms

 Selection sort

  • Very simple and very inefficient algorithm
    • Best, worst and average case: \( n^2 \)
    • Memory: 1 (constant, only for the min element)
    • Stable: No
    • Method: Selection

 Selection sort 

procedure selectionSort( A : list of sortable items )
    n = length(A)
    for i = 0 to n-1 inclusive do
        min = i;

        for j = i+1 to n inclusive do
            if A[j] < A[min]
                min = j    
            end if
        end for
        
        if min != j
            swap(A[j], A[min])
        end if
    end for
end procedure
  • Pseudocode

 Bubble sort​

  • Repeatedly stepping through the list
    • Comparing each pair of adjacent items
    • Swap them if they are in the wrong order
    • Best case: \( n \),
    • Worst and average case: \( n^2 \)
    • Memory: 1
    •  Stable: Yes
    •  Method: Exchanging

 Bubble sort​ 

procedure bubbleSort( A : list of sortable items )
    n = length(A)
    repeat 
        swapped = false
        for i = 1 to n-1 inclusive do
            /* if this pair is out of order */
            if A[i-1] > A[i] then
                /* swap them and remember something changed */
                swap( A[i-1], A[i] )
                swapped = true
            end if
        end for
    until not swapped
end procedure
  • Pseudocode

 Insertion sort

  • Builds the final sorted array one item at a time
    • Best case: n
    • Worst and average case: \( n^2 \)
    • Memory: 1
    • Stable: Yes
    • Method: Insertion

 Insertion sort 

procedure insertionSort( A : list of sortable items )
    i = 1
    while i < length(A)
        j = i
        while j > 0 and A[j-1] > A[j]
            swap A[j] and A[j-1]
            j = j - 1
        end while
        i = i + 1
    end while
end procedure
  • Pseudocode

 Quicksort

  • First divides a large list into two smaller sub-lists then recursively sort the sub-lists
    • Best and average case: \( n*log(n) \)
    • Worst: \( n^2 \)
    • Memory: \( log(n) \) stack space
    • Stable: Depends
    • Method: Partitioning

 Quicksort 

algorithm quicksort(A, lo, hi) is
    if lo < hi then
        p = partition(A, lo, hi)
        quicksort(A, lo, p)
        quicksort(A, p + 1, hi)
  • Pseudocode
algorithm partition(A, lo, hi) is
    pivot = A[lo]
    i = lo - 1
    j = hi + 1
    loop forever
        do
            i = i + 1
        while A[i] < pivot

        do
            j = j - 1
        while A[j] > pivot

        if i >= j then
            return j

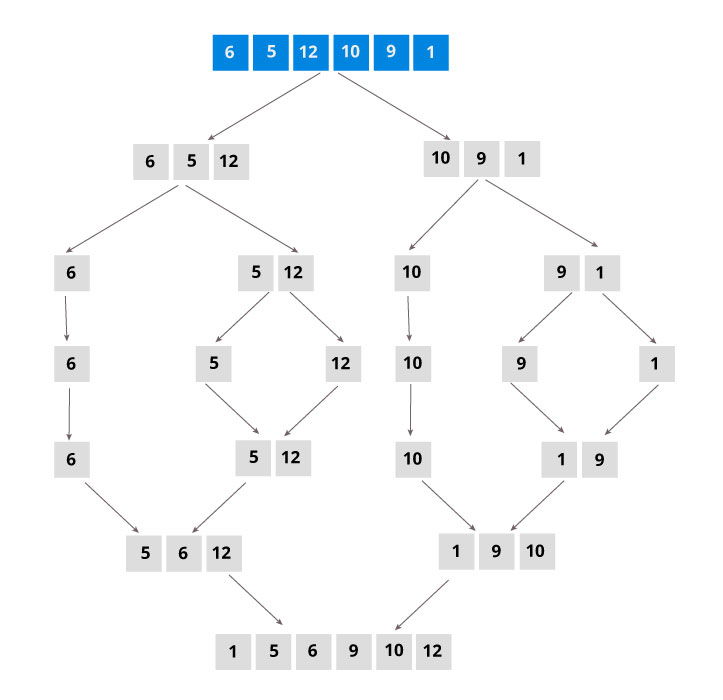
        swap A[i] with A[j]

 Merge Sort​

  • Conceptually, a merge sort works as follows
    • Divide the unsorted list into n sublists, each containing 1 element (list of 1 element is sorted)
    • Repeatedly merge sublists to produce new sublists until there is only 1 sublist remaining
  • Best, average and worst case: \( n*log(n) \)
  • Memory: Depends; worst case is \( n \)
  • Stable: Yes;
  • Method: Merging
  • Highly parallelizable (up to \( O(log(n) \))
    • using the Three Hungarian's Algorithm

 Merge Sort​

 Merge Sort​ 

merge(A, lo, mid, hi)
{ 

    /* Merge A[lo..mid] with A[mid+1..hi] */
    i = lo
    j = mid+1
    for (int k = lo; k <= hi; k++)
 
        /* Copy a[lo..hi] to aux[lo..hi] */
        Aux[k] = A[k];
    for (int k = lo; k <= hi; k++) 

        /* Merge back to a[lo..hi] */
        if (i > mid) A[k] = Aux[j++];
        else if (j > hi ) A[k] = Aux[i++];
        else if (less(Aux[j], Aux[i])) A[k] = Aux[j++];
        else A[k] = Aux[i++];
}
  • Pseudocode

 Merge Sort​ 

sort(A, lo, hi)
{ 
    /* Sort a[lo..hi] */
    if (hi <= lo) return;

    int mid = lo + (hi - lo)/2;
    
    /* Sort left half */
    sort(a, lo, mid); 
    
    /* Sort right half */
    sort(a, mid+1, hi); 

    /* Merge results */
    merge(a, lo, mid, hi); 
}
  • Pseudocode

 Comparison of Sorting Algorithms

  • There are hundreds of sorting algorithms
    • Some of them are:
Name Best Avg Worst Memory Stable
Bubble n n^2  n^2 1 Yes
Insertion n n^2 n^2 1 Yes
Quick n*log(n) n*log(n) n^2 log(n) Depends
Merge n*log(n) n*log(n) n*log(n) n Yes
Heap n*log(n) n*log(n) n*log(n) n No
Bogo n n*n! n*n! 1 No

What is a searching algorithm?

 What is a searching algorithm?

  • An algorithm for finding an item with specified properties among a collection of items
  • Different types of searching algorithms
    • For virtual search spaces
      • satisfy specific mathematical equations
      • try to exploit partial knowledge about structure
    • For sub-structures of a given structure
      • graph, a string, a finite group
      • Search for the max (min) of a function

 Which algorithm

  • What the most people (non-programmers) would think when they need to search a value in a collection
    • Scan all the possibilities and if found return it
    • A big problem with large collections
      • The next exmple is simple enough
      • But imagine thousands or millions of numbers

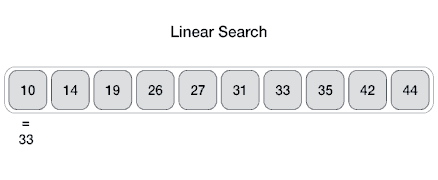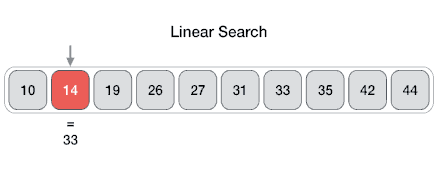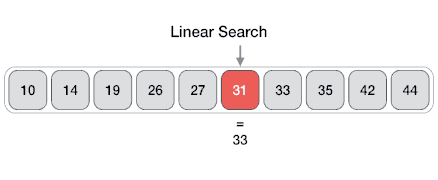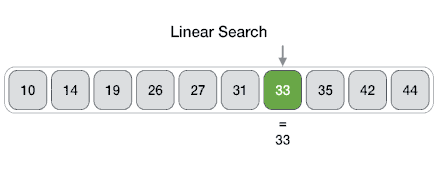
Searching Algorithms

 Linear Search

  • Method for finding a particular value in a list
    • Checking every one of the elements
    • One at a time in sequence
    • Until the desired one is found
  • Worst and average performance: \( O(n) \)
for each item in the list:
     if that item has the desired value,
         stop the search and return the location.
 return nothing.

 Binary Search

  • Finds the position of a specified value within an ordered data structure
  • In each step, compare the input with the middle
    • The algorithm repeats its action to the left or right sub-structure
  • Average performance: \( O(log(n)) \)
  • Example: Recursive binary search

 Binary Search - recursive

binarySearch(A, key, lo, hi)
  if (to < from)
    // set is empty, so return value showing not found
    return KEY_NOT_FOUND
  // calculate midpoint to cut set in half
  middle = midpoint(from, to)
  if (A[middle] > key)
    // key is in lower subset
    return binarySearch(A, key, from, middle - 1)
  else if (A[middle] < key)
    // key is in upper subset
    return binarySearch(A, key, middle + 1, to)
  else
    // key has been found
    return middle
  • Pseudocode

 Binary Search - linear

binarySearch(A, int key)
  while (from <= to)
    //calculate the midpoint for roughly equal partition x/
    middle = midpoint(from, to)
    // determine which subarray to search
    if (A[middle] < key)
      // change from index to search upper subarray
       from = middle + 1
    else if (A[middle] > key)
      // change to index to search lower subarray
       to = middle - 1
    else
      // key found at index middle
      return middle
  return KEY_NOT_FOUND
  • Pseudocode

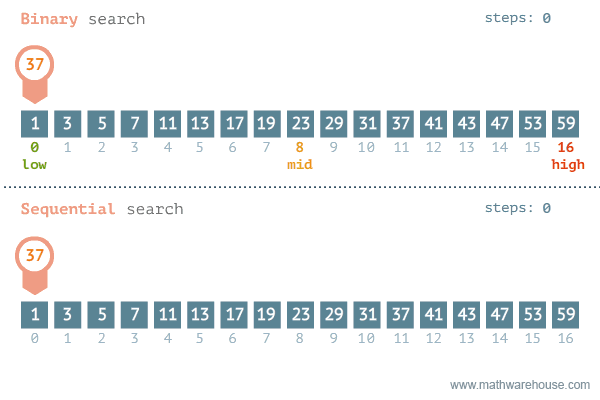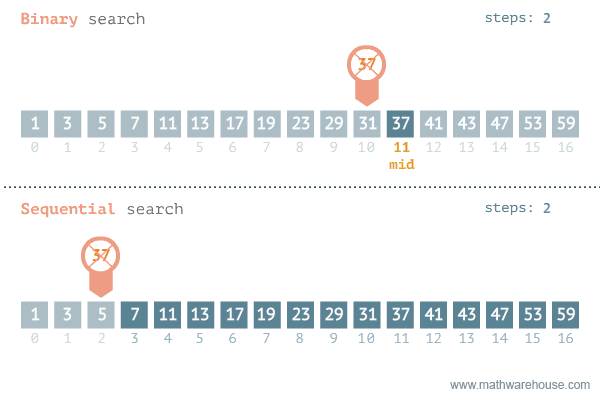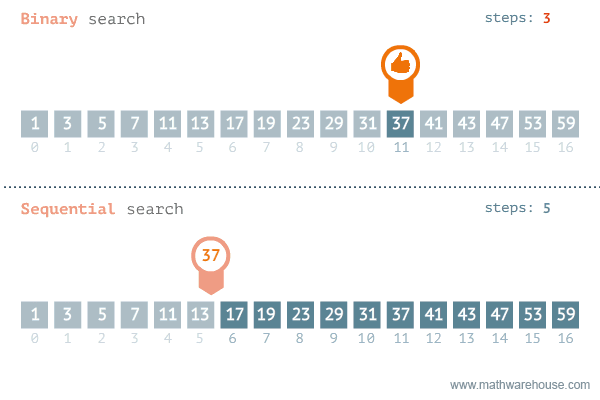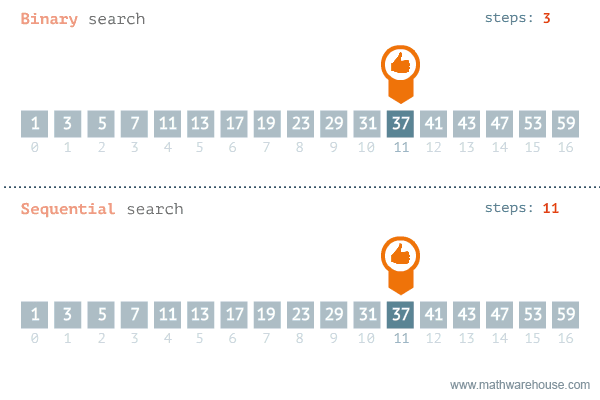
 Linear vs Binary search

Questions?

[C# DSA] Sorting and Searching Algorithms

By telerikacademy

Made with Slides.com

[C# DSA] Sorting and Searching Algorithms

  • 1,365

More from telerikacademy