Analyse spatiale

Concepts, théories et méthodes

 

Thierry FEUILLET
Prof. univ. Caen

L3 Unicaen - 2025-2026

  • Organisation du cours et bibliographie
  • Introduction - A quoi sert l'analyse spatiale ?

  • Chapitre I - Concepts, lois, modèles et théories de l’analyse spatiale

  • Chapitre II - En quoi les données spatiales sont-elles spéciales ?
  • Chapitre III - Les méthodes de l’analyse spatiale

Plan détaillé dispo ici : https://hackmd.io/@tfeuillet/Sknde01T3

Plan

  • 12 semaines 2h CM + 2hTD
  • MCC : 1 CC (01/12) + 1 examen terminal
  • Cours principaux avec moi + 4 ou 5 interventions de collègues

Organisation du cours

  • Pumain, D., Saint-Julien, T. (2010). Analyse spatiale: les localisations. Armand Colin.
  • Pumain, D., Saint-Julien, T. (2010). Analyse spatiale: les interactions. Armand Colin.
  • Feuillet T., Cossart E., Commenges H. (2019). Manuel de géographie quantitative. Armand Colin.

Bibliographie

Introduction : à quoi sert l'analyse spatiale ?

Quelques définitions...

L’analyse spatiale :

  • cherche à caractériser et à comprendre les structures spatiales, les localisations, et leurs processus sous-jacents

  • … + les relations entre les lieux

  •  => Approche nomothétique horizontale - vs approche idiographique, ie verticale

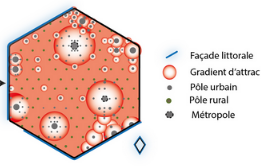
L'analyse spatiale s’appuie sur des théories et des méthodes empiriques spécifiques

Enault et Chatel, 2017

Principaux concepts de l’analyse spatiale :

gradient, discontinuité, hétérogénéité, concentration,

interaction, dispersion/attraction, etc.

Relations structures-processus, ex : concentration = attraction

  • L’analyse spatiale est parfois définie de façon restrictive en géomatique

  • Elle est alors synonyme de géotraitement (opérations sur des géométries)

Warning !

1.2. L'analyse spatiale : une chaîne d'analyses et de traitements

Analyse spatiale

Théories et concepts

Dimension théorique

Données et méthodes

Hypothèses

Outils

Mise en oeuvre

Dimension méthodologique (géomatique)

  • Contraction de géographie et informatique
  • => Traitements informatiques de l'information géographique
  • Parfois appelée science de l'information géographique

La géomatique

  • SI qui intègre, stocke, analyse et affiche l’information géographique

Les systèmes d'information gépographique (SIG)

  • SI qui intègre, stocke, analyse et affiche l’information géographique

  • Les 5 “A” d’un SIG :

    • Acquisition

    • Archivage

    • Analyse

    • Affichage

    • Abstraction (passage du modèle physique au modèle numérique)

Les systèmes d'information gépographique (SIG)

  • L'analyse spatiale a pour but de comprendre/modéliser des localisations d’objets ou de processus dans l’espace
  • L'analyse spatiale encapsule la géomatique (incluant les SIG)
  • Les théories spatiales (chapitre 1) permettent au préalable de poser des hypothèses sur les localisations

Pour résumer

  • A gagner des élections
  • A gagner de l'argent
  • A sauver des vies
  • A sauver des animaux
  • A gagner du temps
  • A valider sa L3 et trouver un job

1.3. A quoi sert l'analyse spatiale ?

A gagner des élections (gerrymandering)

  • Le gerrymandering désigne le découpage électoral partisan, ou charcutage électoral
  • Le nom provient du nom du gouverneur américain Gerry (1811) et de mandering pour salamandre

Exemple récent avec Trump

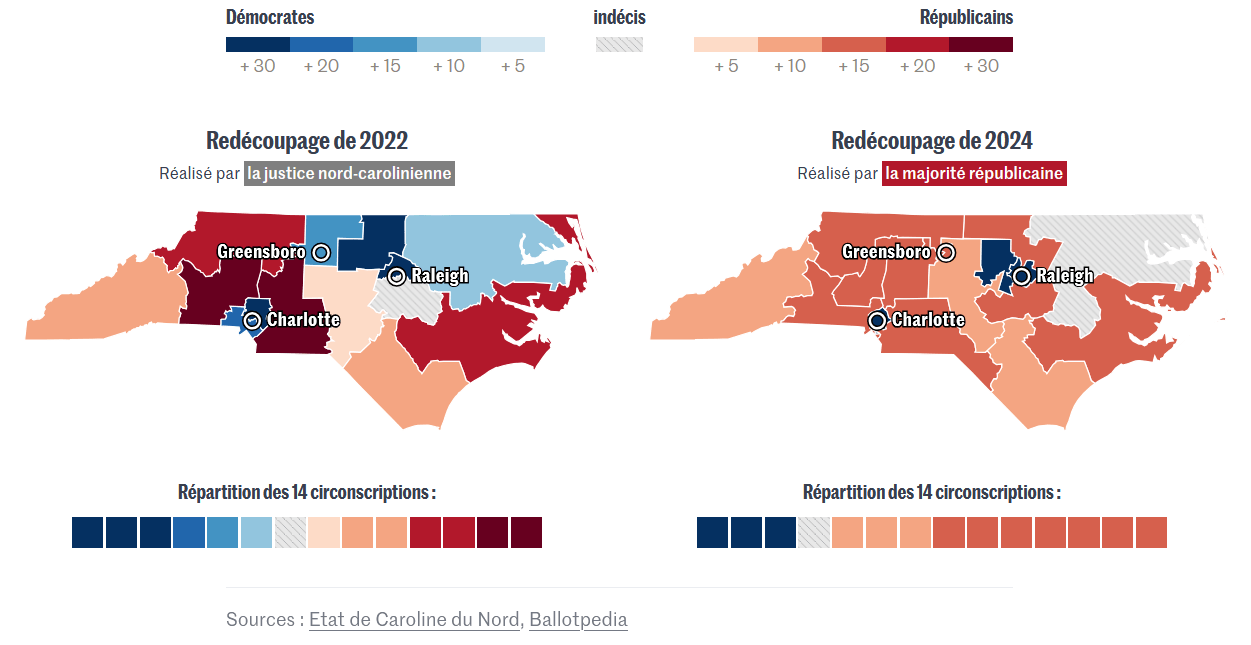
A gagner des élections (gerrymandering)

  • Ce problème est bien connu en géographie quantitative
  • C'est le MAUP (modifiable areal unit problem) ou plus largement le biais d'agrégation, ou erreur écologique
  • Ce sera l'objet du chapitre 2 (le spatial est spécial)

A gagner de l'argent (optimisation spatiale)

  • Une branche de l'analyse spatiale s'intéresse à l'optimisation spatiale
  • Cela consiste à déterminer des localisations optimales, ie permettant de minimiser une fonction objectif (par ex perte d'argent)
  • Appliquée au domaine commercial, il s'agit de géomarketing

A gagner de l'argent (optimisation spatiale)

  • La recherche de localisations optimales s'appuie sur deux types de modèles :
    • Les modèles gravitaires
    • Les modèles de localisation-allocation

Modèles gravitaires

  • Dérivent de la loi de Newton
  • Modèles d'interaction spatiale

Modèles de localisation

  • Localisation optimale de points de vente
  • Minimisation des couts de déplacement des clients (optimisation)
  • Géographie de la santé / épidémiologie spatiale
  • Analyse de la distribution spatiale des maladies et de leurs facteurs

A sauver des vies

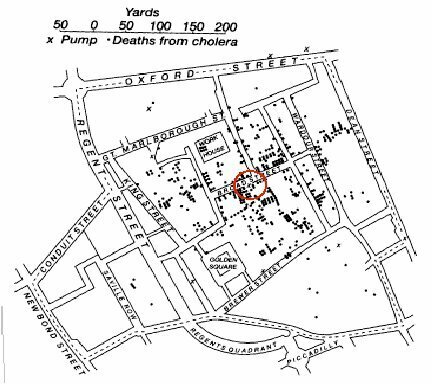
Exemple de l'épidémie de choléra de 1854 à Londres

A sauver des vies

Source wikipédia

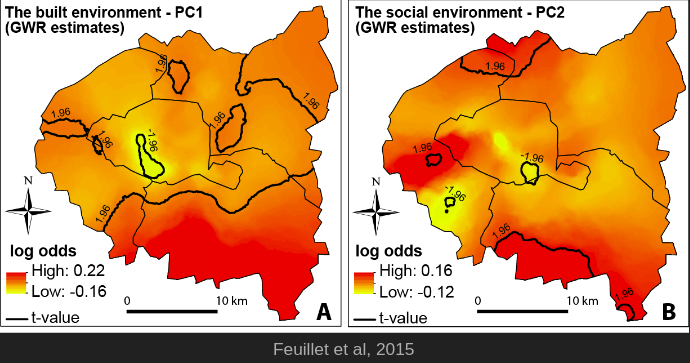
Spatialisation des facteurs de santé pour des interventions de santé publique ciblées

A sauver des vies

  • Il existe de nombreuses applications d'analyse spatiale en biogéographie et en écologie
  • Beaucoup s'appuient sur des théories d'écologie spatiale et théorie des graphes (connectivité écologique)

A sauver des animaux

  • Exemple de théorie d'écologie spatiale : la théorie biogéographique des îles

A sauver des animaux

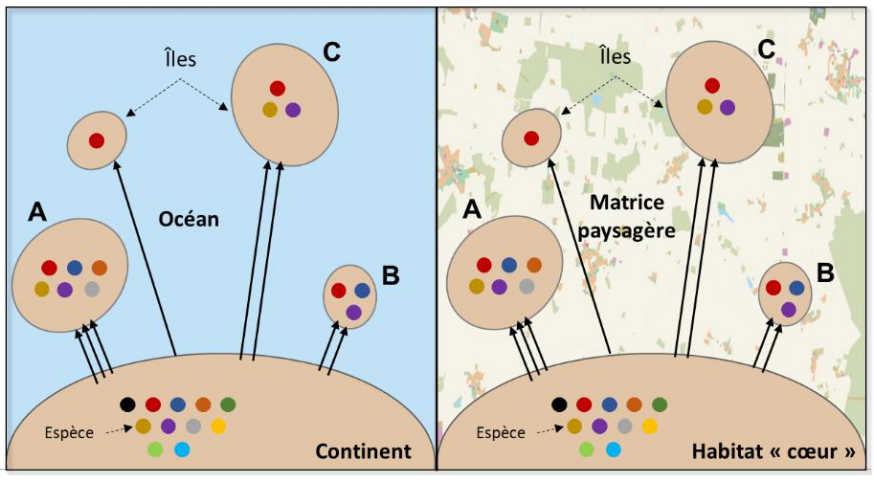
Clauzel 2021

  • Exemple de modélisation de réseaux écologiques

A sauver des animaux

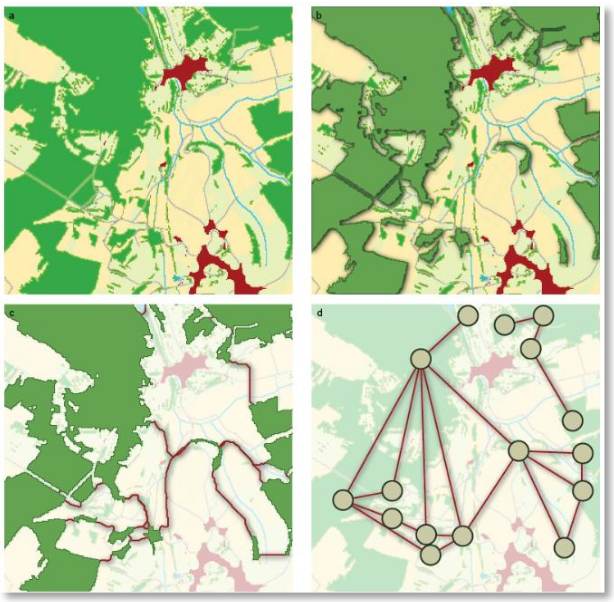
- Noeuds = taches d'habitat

- Liens = chemins de moindre coût

 

Girardet et Clauzel, 2018

  • Analyse de réseaux (chemins de moindre coût)
  • Modèles d'interaction spatiale pour prédire les flux de navetteurs

A gagner du temps

Chapitre I

Concepts, lois, modèles et théories de l'analyse spatiale

  • Concept : terme associé à des idées plus ou moins abstraites, à des théories, mais construit de façon formelle
  • Loi : énoncé universel et non accidentel, valable partout et tout le temps (en SHS : presque toujours vrai - principe, conjecture, régularité)
  • Modèle : outil dérivant des lois et permettant d'extraire des régularités utiles pour la compréhension d'un phénomène
  • Théorie : ensemble structuré et formel de lois

D'abord les méta-concepts

  • Avant Darwin, on comprenait des choses mais sans les relier dans un cadre explicatif global
  • Par exemple, on constatait que les espèces s'adaptaient à leur milieu (transformisme de Lamarck)
  • Ceci est une loi, mais pas une théorie

Exemple de théorie : l'évolution des espèces

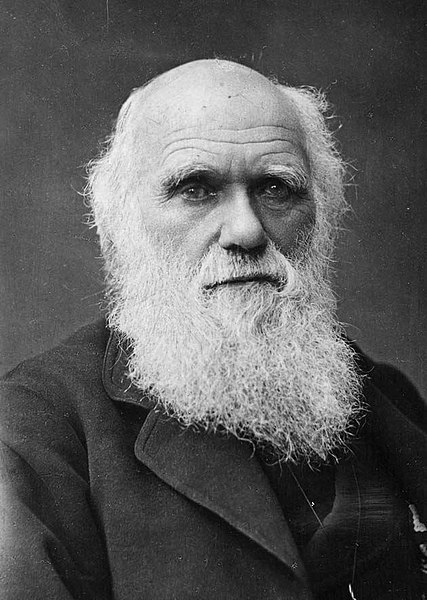
  • Darwin a remis les lois en ordre dans un cadre explicatif :
    1. Les espèces luttent pour leur survie (car elles sont trop nombreuses)
    2. Il existe une hétérogénéité individuelle

Exemple de théorie : l'évolution des espèces

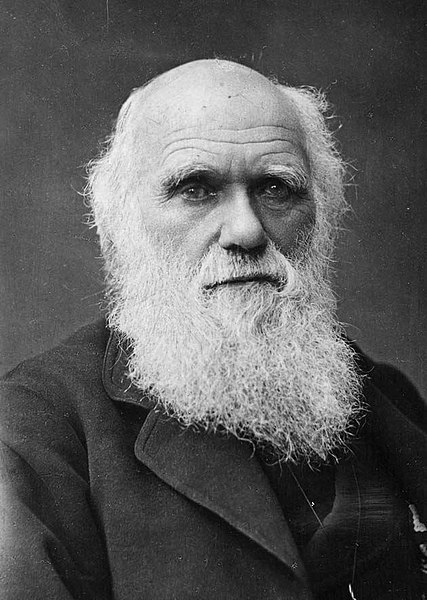
  • Darwin a remis les lois en ordre dans un cadre explicatif :
    • 3. Les individus les mieux adaptés sont sélectionnés
    • 4. Les caractères sont héréditaires

Exemple de théorie : l'évolution des espèces

En géographie, il y a beaucoup de lois mais peu de théories !

Pourquoi modéliser en géographie ?

  • Avant 1950, la géographie consistait principalement en une compilation d'observations locales/régionales (approche idiograhique)
  • Après ~1950, on a commencé à chercher à extraire des régularités ou des lois de l'ensemble de ces observations
  • C'est la révolution quantitative (début de la géographie quantitative)

Un peu d'historique

  • La démarche de la géographie quantitative est principalement nomothétique et abductive
  • Nomothétique : tête bien faite - recherche de lois/régularités
  • Abductive : compromis entre approche inductive et déductive
  • Approche formalisée dans le cadre de l'analyse exploratoire de données spatiales (ESDA)

Démarche nomothétique et abductive

  • La modélisation est particulièrement utile pour formaliser les propriétés et les relations entre objets géographiques
  • En d'autres termes, pour décrire et expliquer les localisations (ie analyse spatiale)
  • Modélisation mathématique/statistique et modélisation dynamique

Démarche nomothétique et abductive

1.1. Les lois de la géographie

Dépendance spatiale

#1

Hétérogénéité spatiale

#2

Lois d'échelle

#3

Autres lois

#4

La première loi de Tobler

〞

Everything is related to everything else, but near things are more related than distant things

– Waldo Tobler, 1970

Waldo Tobler (1930-2018)

  • Loi fondamentale en géographie qui détermine notamment le modèle gravitaire

La première loi de Tobler

F_{ij} = K.( \frac{M_{i}.M_{j}}{d_{ij}^{a}} )
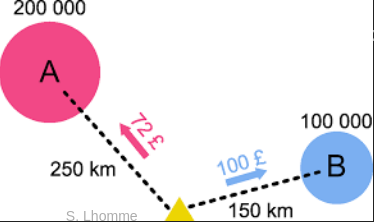
  • Plus largement, cette loi est associée à l'autocorrélation spatiale
  • Les lieux proches se ressemblent davantage que les lieux éloignées
  • Cette loi est intrinsèquement liée à la notion de distance...
  • ... et donc à des processus horizontaux

La première loi de Tobler

  • Différence entre dépendance spatiale et autocorrélation spatiale ?
  • L'une implique des processus, l'autre décrit uniquement des structures
  • Dans tous les cas, cette loi est descriptive et non explicative (cf. théorie)

La première loi de Tobler

  • A noter que cette loi a ses équivalents dans d'autres disciplines
  • En histoire (path dependence), en sociologie, etc.

La première loi de Tobler

  • Enoncé : aucun lieu n'est représentatif de tous les autres, ie toute chose varie selon la localisation

Deuxième loi : l'hétérogénéité spatiale

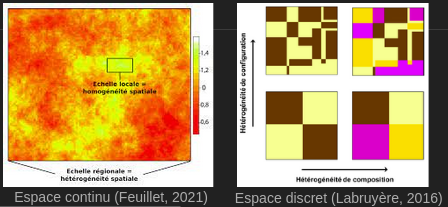
  • Implication : les observations varient nécessairement selon l’échelle d’analyse et l’étendue de l’espace étudié => biais d’agrégation (i.e. erreur écologique)

Deuxième loi : l'hétérogénéité spatiale

  • L'échelle est définie selon deux composantes :
    • L'étendue
    • La résolution
  • La résolution est intrinsèquement liée au principe d'agrégation

Définition de l'échelle

  • Implication statistique : non-stationnarité spatiale des paramètres

Deuxième loi : l'hétérogénéité spatiale

  • Elles englobent toutes les régularités observées lors de changements d'échelle
  • Elles correspondent à la forme de la relation mesurée entre deux variables caractérisant des objets à des échelles différentes (invariance d'échelle)

Les lois d'échelle

  • Cette relation est appelée "élasticité"
  • L'élasticité est un rapport de variations :

 

 

  • On peut ensuite écrire la relation entre les deux variables avec e en exposant

Les lois d'échelle

e = \frac{\frac{d(x)}{x}} {\frac{d(y)}{y}}
y = k.x^e
  • Si e = 1, relation proportionnelle
  • Si e > 1, relation supra-linéaire
  • Si e < 1, relation sub-linéaire

Les lois d'échelle

  • Exemple en modélisation urbaine : on mesure la relation entre la taille des villes et différentes quantités

Les lois d'échelle

Cottineau et al., 2017

  • Fractales : est fractale toute structure qui se déploie sur plusieurs échelles (Mandelbrot)

Autres lois

  • Loi de Zipf : loi rang-taille (ou loi puissance négative, ou loi de Pareto) fonctionnant notamment pour la distribution des villes
  • Loi de Zahavi : le budget temps de transport dans une ville est constant
  • Loi de Clark : la relation entre la densité de population et la distance au centre-ville est exponentielle négative

Autres lois

  • Loi de Zipf :
    où A est la taille de la plus grande ville et alpha le paramètre à estimer
     

     
  • Loi de Clark :
    où y est la densité et x la distance au centre

Equations

y = A.x^{-\alpha}
y = Ax^{-\alpha}
y = Ae^{bx}
  • Durand-Dastès (1931-2021) était un géographe français théoricien
  • Il a proposé une grille de lecture des localisations, relativement universelle
  • C'est un cadre explicatif théorique car il relie les localisations aux processus sous-jacents

1.2. La théorie des localisations de Durand-Dastès

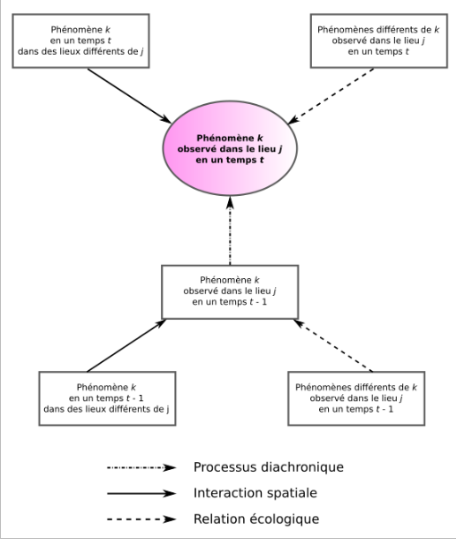
Durand-Dastès (2001)

La localisation d'un phénomène k dans un lieu j en un temps t dépend :

  • de processus horizontaux
  • de processus verticaux (ou écologiques)
  • de processus diachroniques
  • Les effets horizontaux (interactions spatiales) impliquent la notion de distance
  • Les effets verticaux (effets de contexte) impliquent la notion d'appartenance

Processus verticaux : les effets de contexte

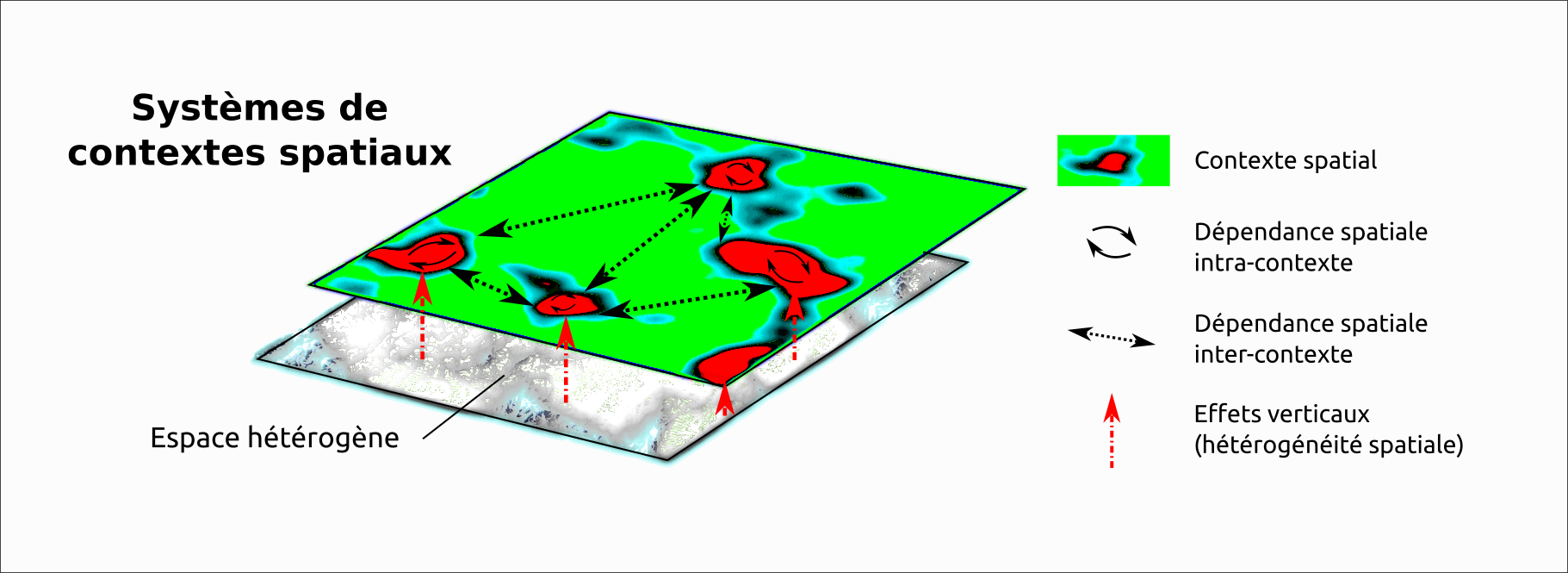
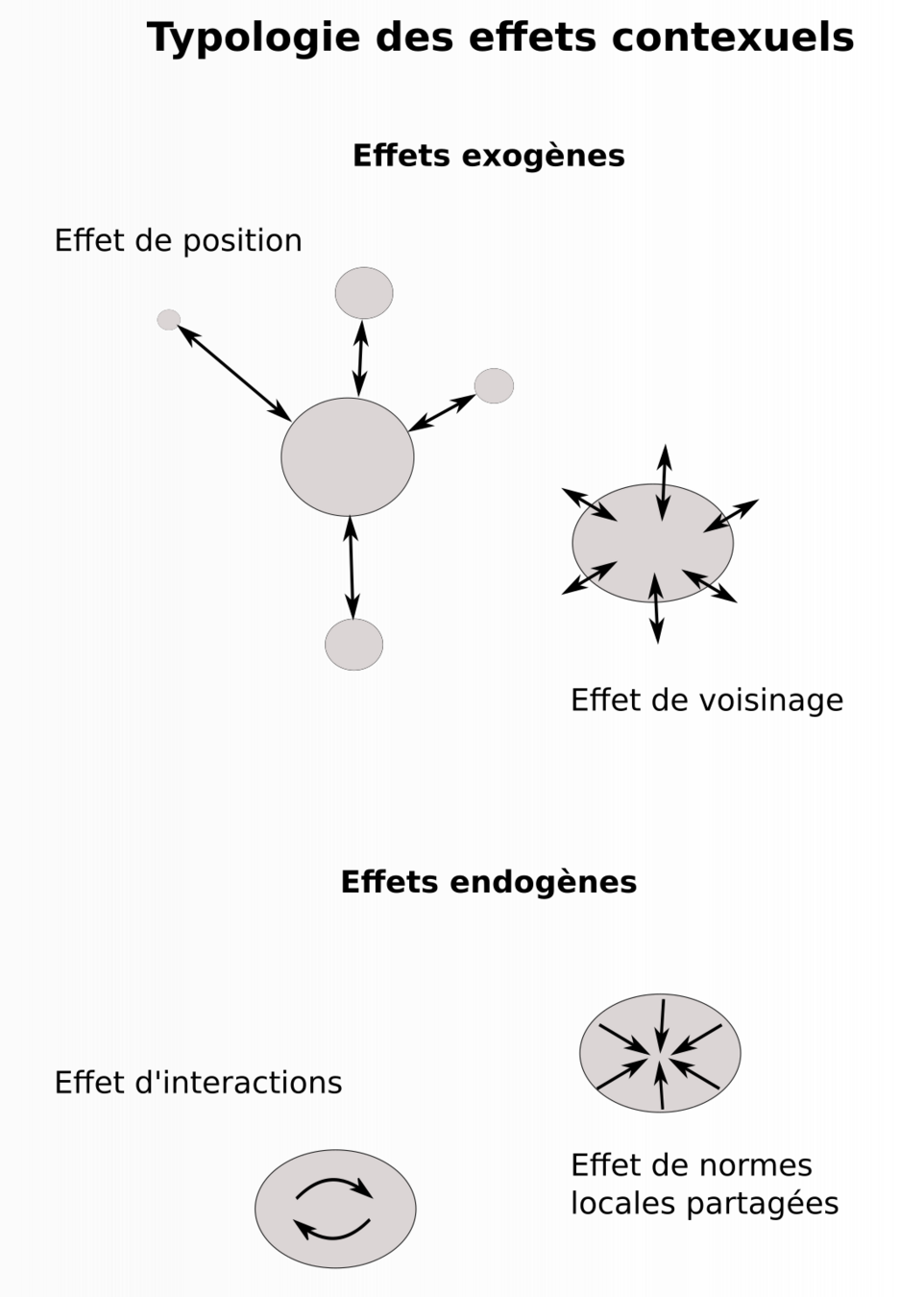
Typologie des effets de contexte

Inspiré des effets de Manski (1993)

Feuillet (2021)

  • La description ne suffit pas, l'explication est nécessaire
  • Il faut chercher les causes des structures spatiales
  • Mais les processus sous-jacents sont souvent complexes, multiples et multi-scalaires

Relier les structures spatiales aux processus

ssc

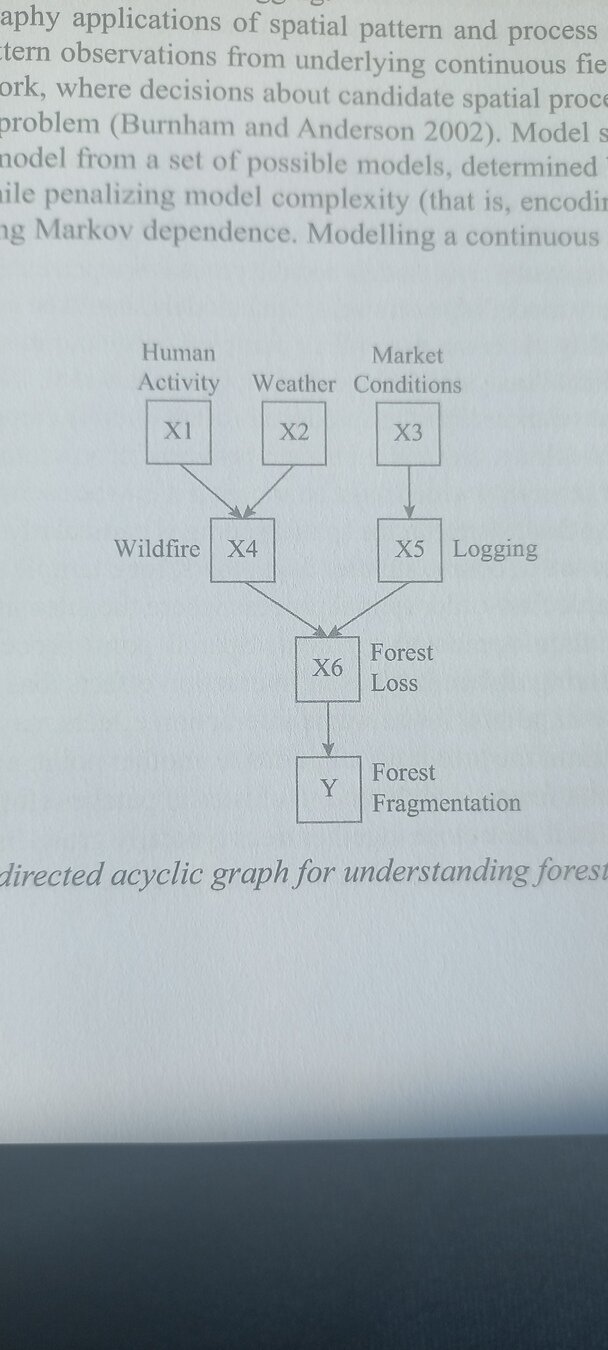
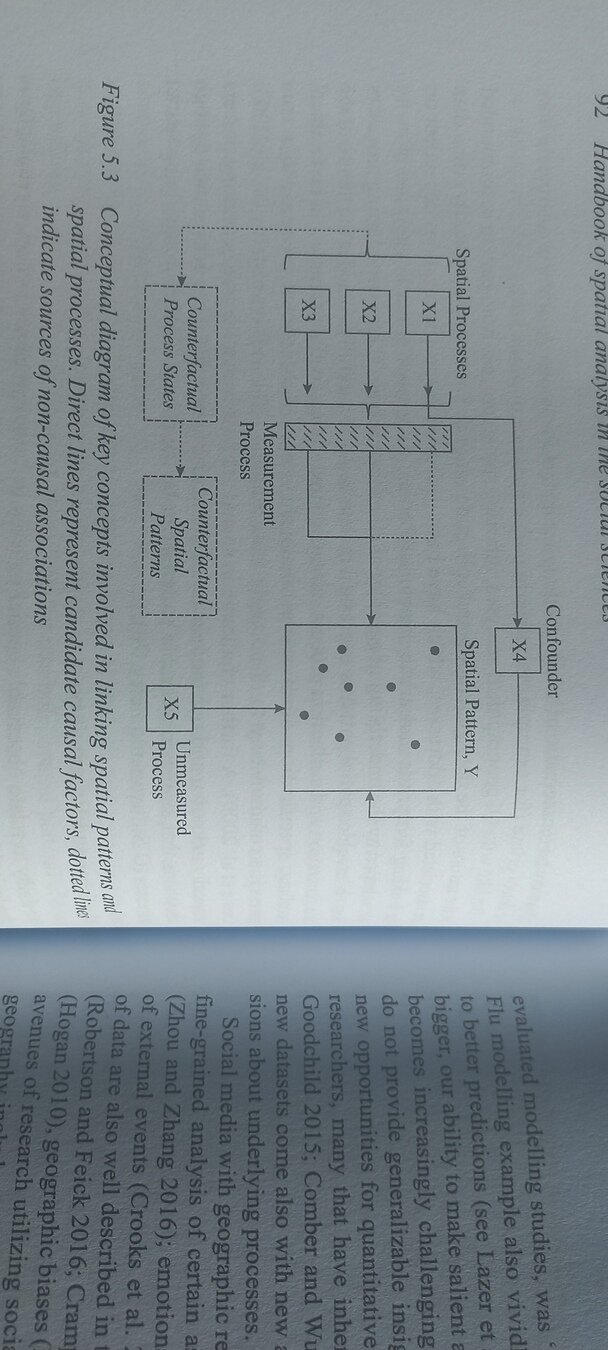
Les chemins de la causalité

Chemins souvent complexes

Robinson, 2023

Illustration

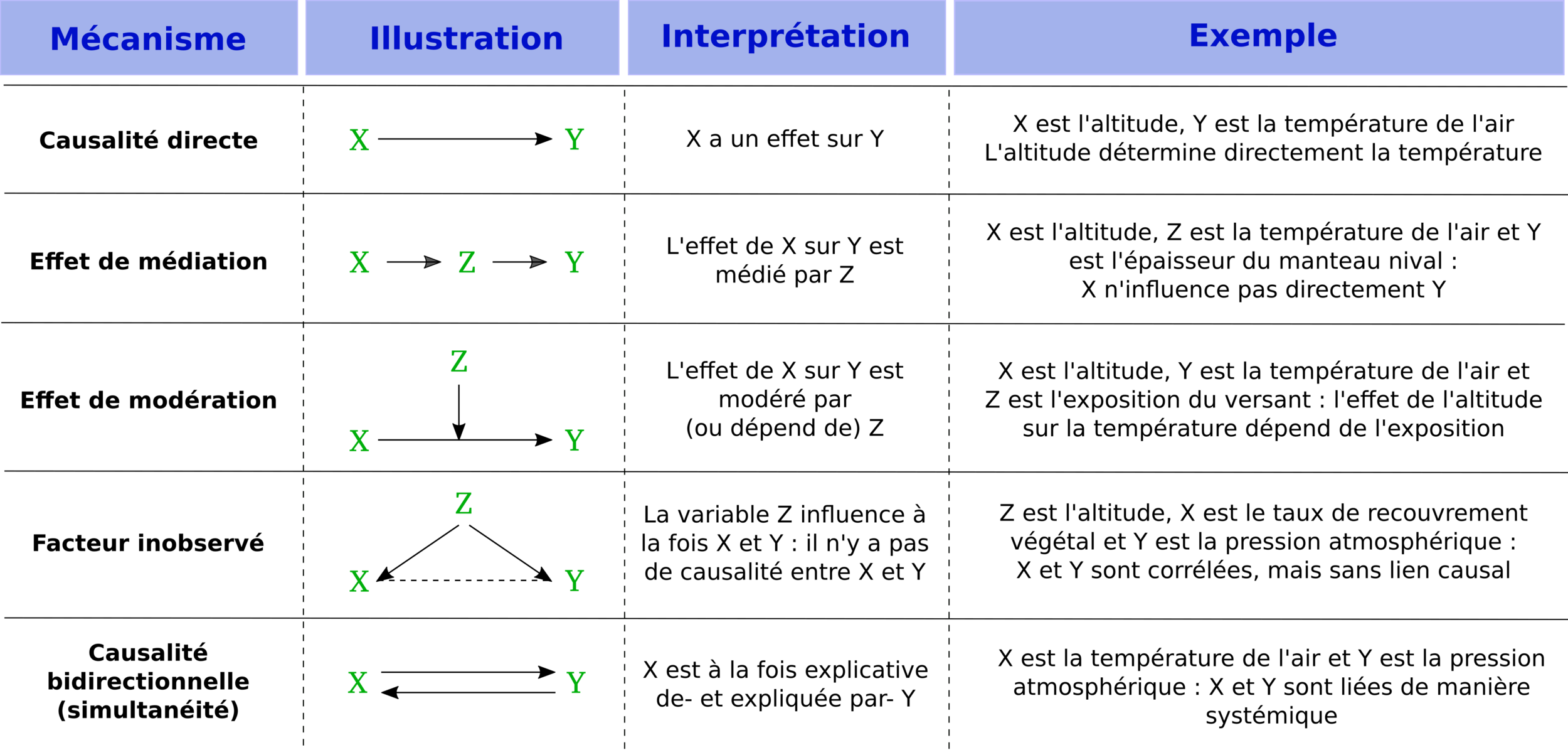
Feuillet et al., 2019

- Les deux principales lois de la géographie sont la dépendance spatiale (interactions spatiales) et l'hétérogénéité spatiale

- Il y a des lois et des modèles en géographie, mais peu de théories globales des localisations (ex Durand-Dastès)

- Globalement, l'analyse spatiale cherche à caractériser les structures spatiales et à les relier aux processus sous-jacents

Résumé du chapitre I

  • Les approches statistiques sont indispensables pour caractériser et objectiver de grandes masses de données
  • Quand les données sont localisées (ie associées à des coordonnées géographiques), des problèmes spécifiques se posent

Chapitre II
Le spatial est spécial

2.1. Biais et erreurs en statistiques

https://quizlet.com/be/497546113/chapitre-8-precision-et-validite-en-epidemiologie-flash-cards/

2.2. Spécificités des données géographiques

  • Les données géographiques sont hétérogènes => biais inférentiel en cas de mauvais échantillonnage spatial
  • Les données géographiques sont souvent agrégées => biais d'agrégation

Echantillonnage spatial

Thiele et al, 2023 (http://dx.doi.org/10.1007/s10980-023-01605-1)

2.3. Biais d'agrégation

  • En géographie humaine, on ne dispose que rarement des données au niveau individuel (secret statistique)
  • Les données sont donc agrégées (quartier, commune, département, etc.)

2.3. Biais d'agrégation

  • L'agrégation des données a des implications sur les calculs statistiques
  • Ce problème est connu sous le nom de MAUP (modifiable areal unit problem)

Cas extrême de MAUP : le paradoxe de Simpson

  • Il arrive que la relation statistique soit inversée dans les sous-groupes d'un échantillon

L'erreur écologique

  • L'erreur écologique consiste à observer une corrélation à un certain niveau d'agrégation et à en déduire qu'elle existe à d'autres niveaux
  • Niveau écologique = niveau agrégé (rien à voir avec l'écologie)
  • Formalisée par Robinson en 1950 : relation négative entre l'illettrisme et le taux d'immigrés au niveau agrégé, inverse sinon

L'erreur écologique

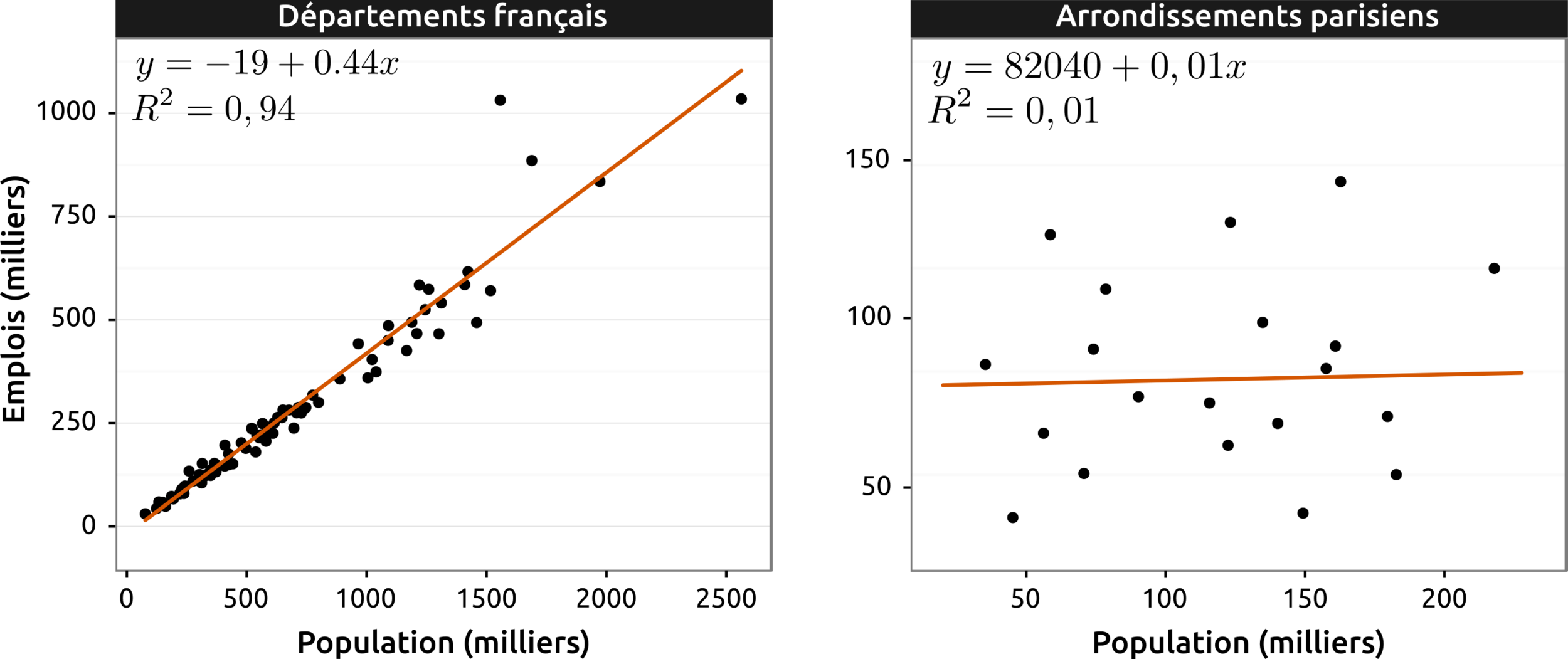
Manuel de géographie quantitative (Feuillet et al., 2019)

L'erreur écologique

  • Les corrélations au niveau individuel s'expliquent principalement par des facteurs de niveau individuel, même raisonnement pour les niveaux écologiques
  • Dans la mesure du possible, il faut toujours essayer de disposer d'information au niveau le plus fin, et ne pas inférer de résultats empiriques à une autre échelle que celle analysée

L'erreur atomiste

  • L'erreur atomiste consiste à ne pas considérer le contexte dans lequel évoluent les individus (ie rester au niveau individuel)
  • En effet, certaines observations au niveau individuel s'expliquent par des processus au niveau agrégé (ex. effets corrélés de Manski, effet contextuel)
  • Le niveau d'un élève dépend de facteurs individuels ET du niveau moyen de la classe
  • 3.1. Rappels basiques de statistiques
  • 3.2. Caractériser les structures spatiales
  • 3.3. Modéliser les processus sous-jacents

 

Chapitre III
Les méthodes de l'analyse spatiale

  • Les statistiques représentent l'ensemble des méthodes permettant d'étudier la variation des données
  • L'analyse spatiale est indissociable de l'analyse statistique

 

3.1. Rappels basiques de statistiques

Les types de variables

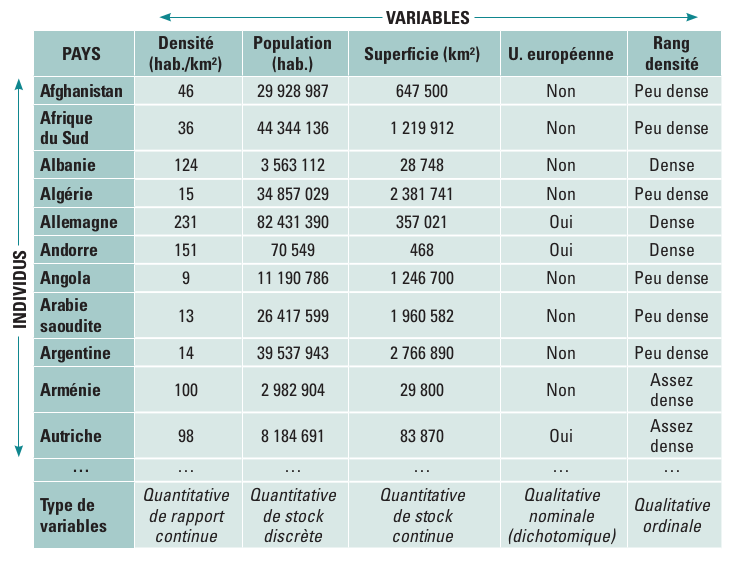
Paramètres de position et de dispersion

  • Paramètres de position : décrire une variable par ses valeurs centrales
  • Paramètres de dispersion : décrire une variable par la dispersion de ses valeurs autour d'une valeur centrale

 

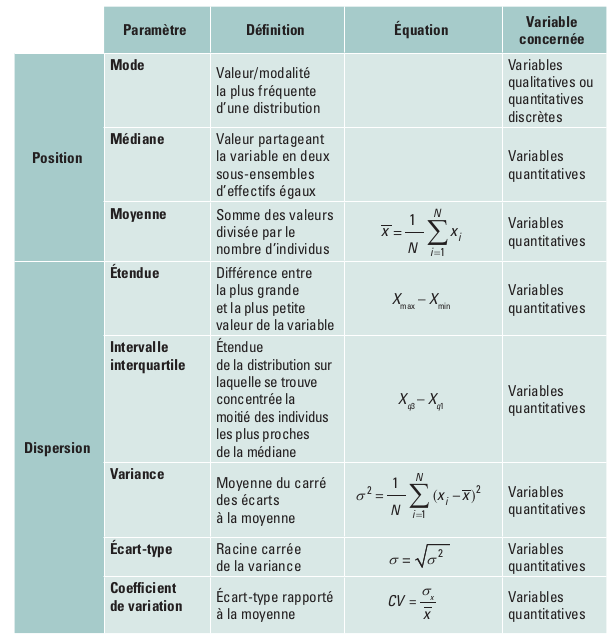
Corrélation

  • La corrélation désigne la covariation de deux variables (cf. élasticité)
  • Quand l'une augmente, l'autre aussi et inversement
  • Le nuage de points (graphique cartésien) est un bon moyen visuel pour caractériser des corrélations

 

Corrélation

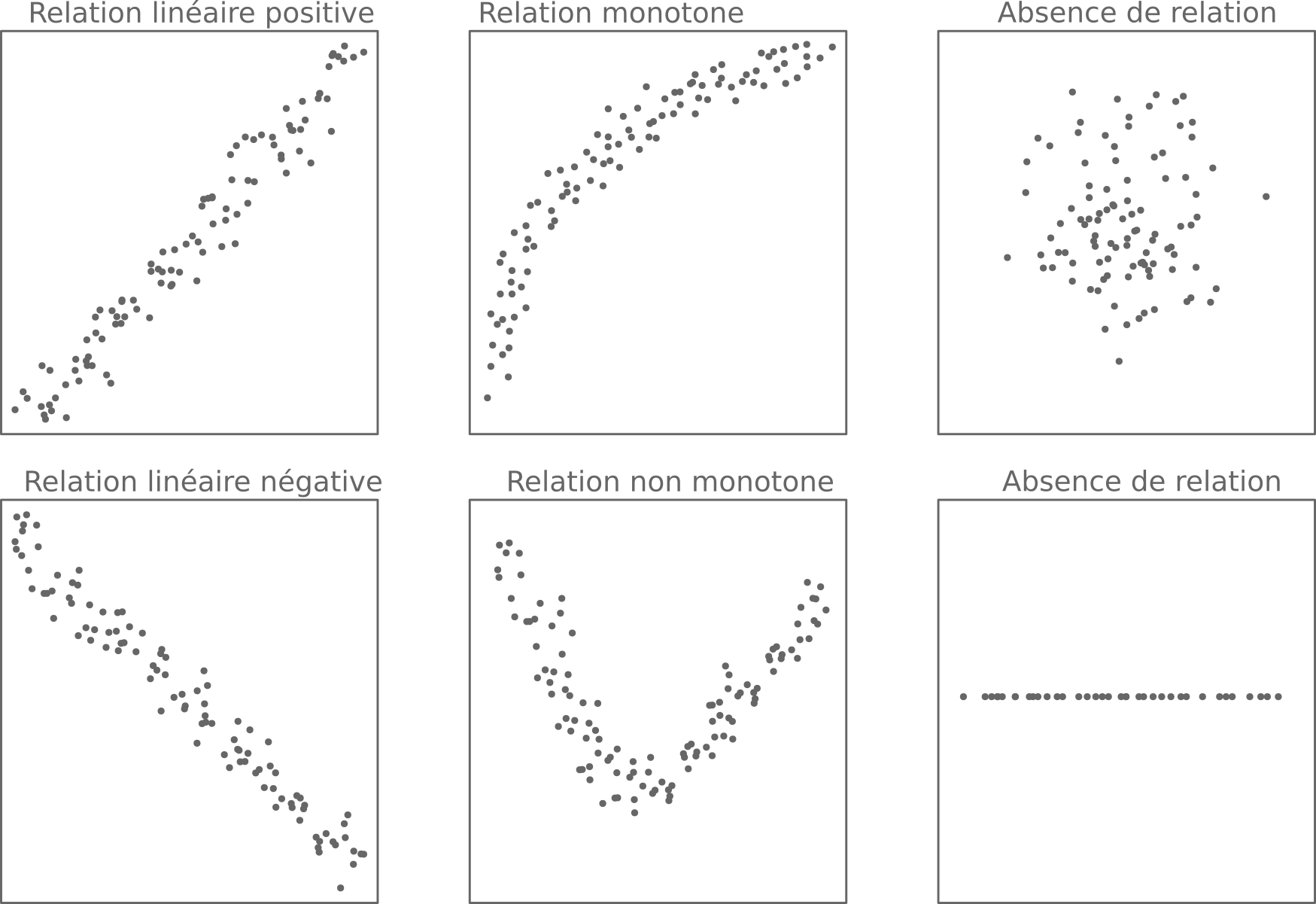
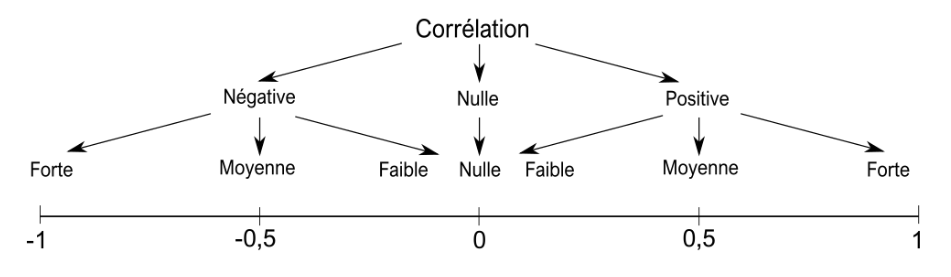
Corrélation

  • On peut aussi la quantifier à travers le coefficient de corrélation (noté R)

 

 

 

r = \frac{ \sum_{i=1}^{n}(x_i-\bar{x})(y_i-\bar{y}) }{% \sqrt{\sum_{i=1}^{n}(x_i-\bar{x})^2}\sqrt{\sum_{i=1}^{n}(y_i-\bar{y})^2}}

Corrélation spatiale

  • Désigne la co-occurrence ou la covariation spatiale de deux phénomènes
  • Fondamental pour relier les structures aux processus

 

 

 

Corrélation spatiale

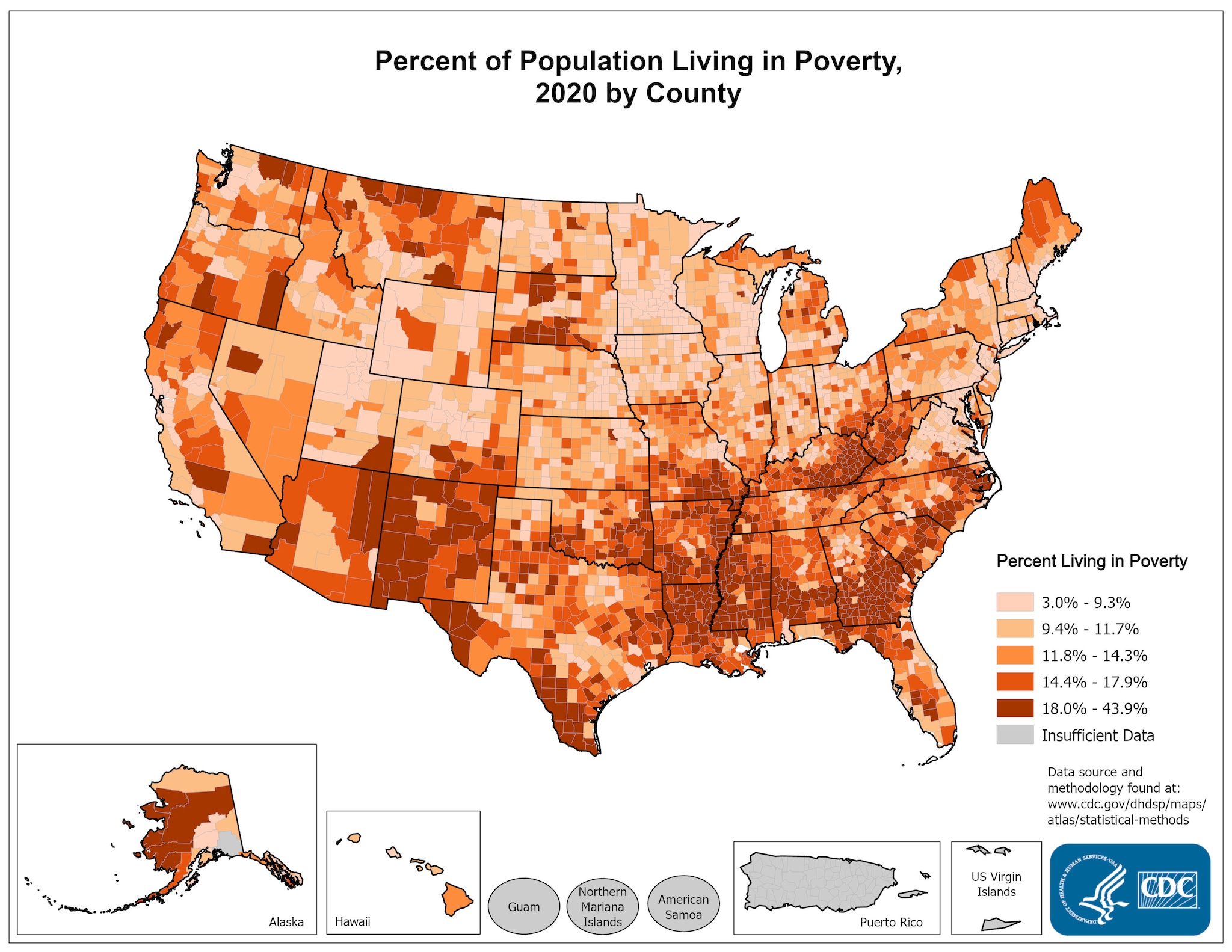
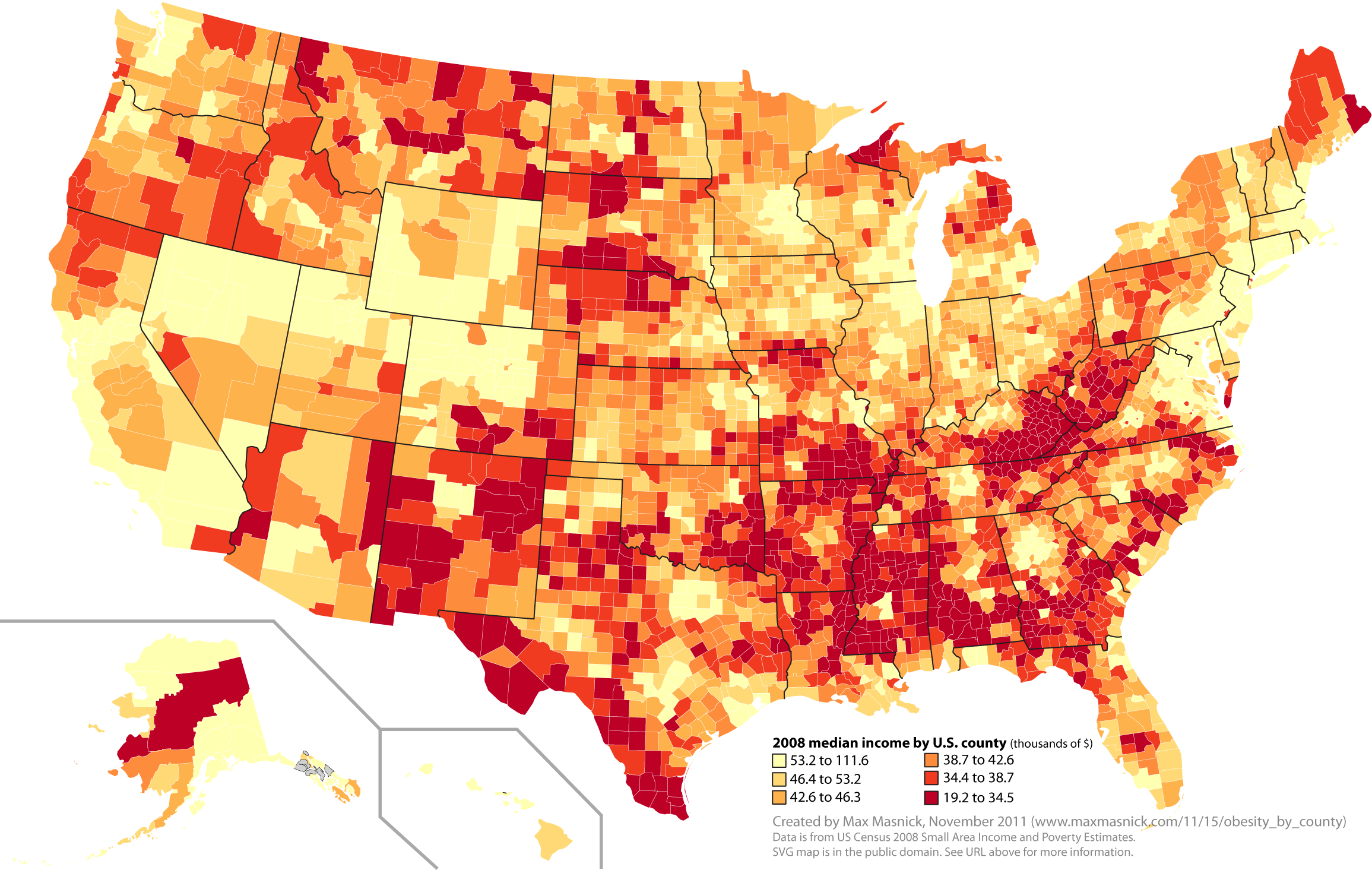
Obesity rate

https://www.maxmasnick.com/2011/11/15/obesity_by_county/

Régression linéaire

  • Méthode servant à modéliser la relation entre des variables

 

 

 

Régression linéaire

  • Méthode servant à modéliser la relation entre des variables

 

 

 

Incertitude et inférence

  • En géographie, les données sont très souvent :
    1. Imprécise (incertitude)
    2. Incomplète (inférence)
  • Les résultats empiriques sont donc associés à des probabilités d'erreurs ou de biais
  • Il est indispensable de toujours bien comprendre comment la donnée traitée à été construite, et ses limites

 

 

 

Incertitude et inférence

  • Pourquoi travaille-t-on sur des échantillons seulement ?
    • Données inacessibles
    • Population trop grande
    • Processus trop couteux
  • La statistique inférentielle consiste à généraliser les résultats issus d'un échantillon, à la population

 

 

 

  • L'inférence est associée à des marges d'erreur
  • Par exemple : les sondages électoraux
  • L'inférence est associée à la notion de significativité : si la marge d'erreur est trop grande, le résultat n'est pas significatif

Inférence statistique

  • Heureusement, il existe des lois en statistique qui nous permettent de faire de l'inférence !
  • Tout d'abord, la loi des grands nombres : elle énonce que quand un échantillon est assez grand, sa moyenne tend vers la moyenne théorique
  • Exemple des lancés de dés
  • Simulation : https://analytics.huma-num.fr/geographie-cites/SimulatR/

Le théorème central limite

  • Les variations observées à chaque tirage représentent la distribution d'échantillonnage de la moyenne
  • le TCL stipule que la distribution des moyennes d'échantillons est normale, de moyenne mu (vraie valeur) et d'un écart-type appelé "erreur standard"
  • Or on connait les propriétés théoriques de la distribution normale
  • La définition des aires sous cette courbe donne les intervalles de confiance d'une estimation

Le théorème central limite

Le théorème central limite

  • Les élections : 18% d'intention de votes pour Jospin en 2002
  • Il y a donc 95% de chances pour que le résultat final soit compris entre p - 2σp et p + 2σp
  • Soit entre 15,6% et 20,4% (résultat final : 16,1%)

Exemples d'applications du TCL

  • Dans une étude sur l'obésité à Paris, nous avons calculé un IMC moyen de 22,9 (sd = 4,1) sur un échantillon de 3938 individus
  • Il y a donc 95% de chances pour que l'IMC moyen des français soit compris entre m +/- 2*(σx/rac(n))
  • [22,9 - 2*(4,1/rac(3938)) ; 22,9 - 2*(4,1/rac(3938))] = [22,9 - 0,13 ; 22,9 + 0,13] => [22,77 ; 23.03]
  • Pourquoi ce raisonnement est-il faux ?

Exemples d'applications du TCL

  • Tout dépend de la qualité de l'échantillonnage spatial, car la moyenne calculée dans le 93 est de 24,7...

Exemples d'applications du TCL

Thiele et al, 2023 (http://dx.doi.org/10.1007/s10980-023-01605-1)

  • Il faut distinguer deux grands types d'information spatiale :
    • Des événements ou objets non marqués (des points sans attributs)
    • Des valeurs (attributs) associées à des points (événements marqués), des lignes ou des surfaces (données agrégées) spatialisées
    • Les valeurs peuvent être continues (géostatistique) ou non

3.2. Caractériser les structures spatiales

  • Les méthodes de caractérisation des structures spatiales dépendent de la nature des données et de leurs processus générateurs
  • Pour les événements, on va principalement estimer des distributions, des densités et des degrés d'agrégation
  • Pour les valeurs, on va s'intéresser aux degrés de ressemblance entre voisins

3.2. Caractériser les structures spatiales

  • Si vos données ne sont pas exhaustives, certaines de ces méthodes ne seront pas adaptées !

Warning

  • On peut tout d'abord calculer le point moyen d'un semis de points (moyenne des coordonnées de tous les points)
  • C'est le point G !

Caractériser des distributions d'objets

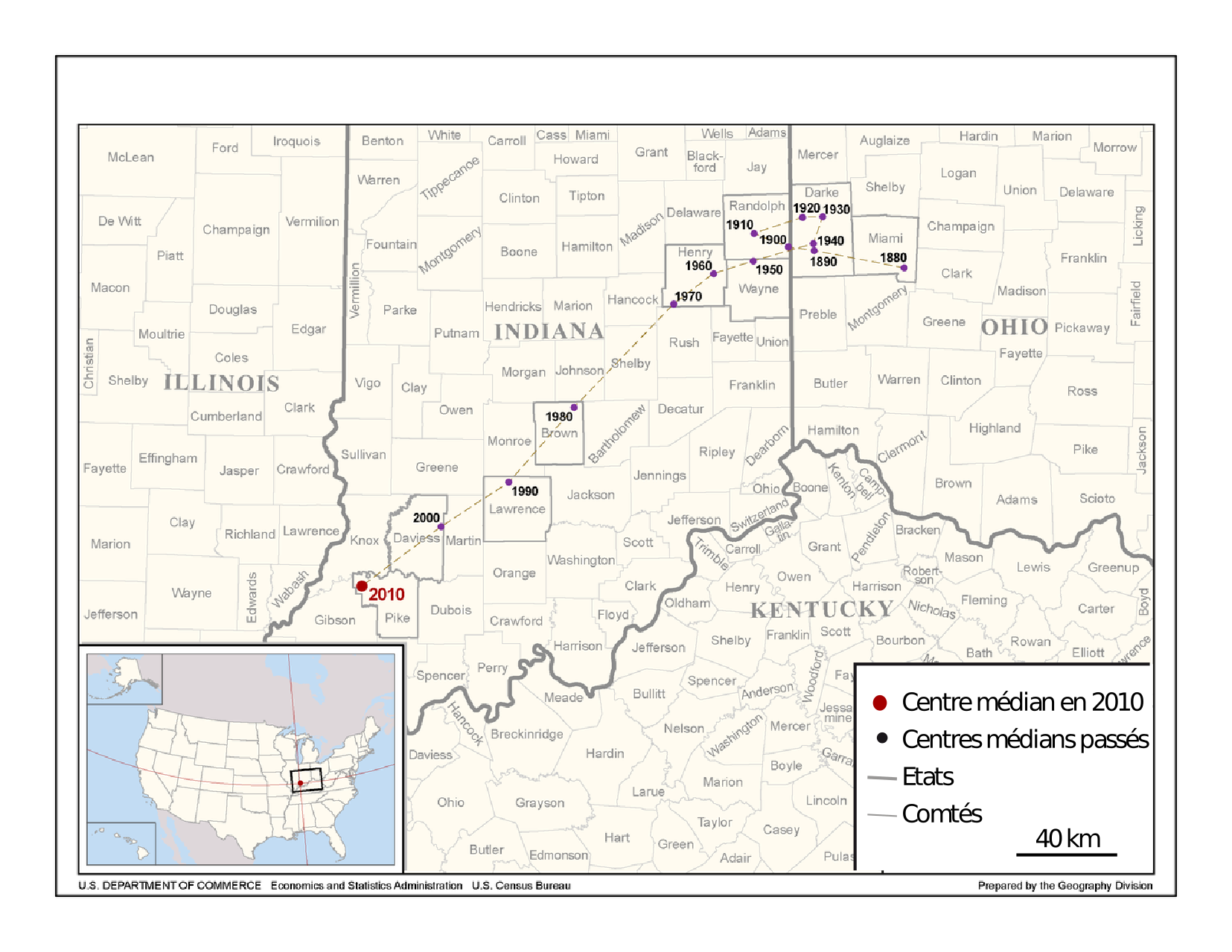
Feuillet et al., 2019

  • On peut aussi calculer des ellipses

Caractériser des distributions d'objets

Feuillet et al., 2019, Manuel de géographie quantitative

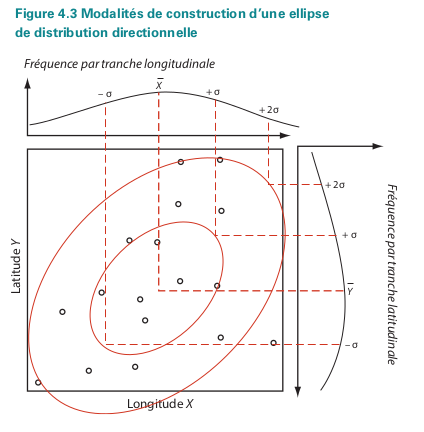
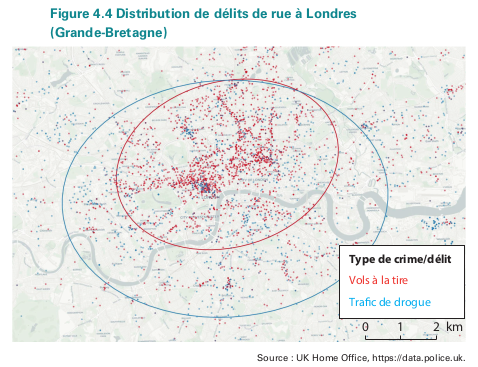
  • Très fréquent quand on étudie des données ponctuelles
  • Deux méthodes principales
    • Densités dans des mailles/surfaces
    • Densités de noyau (zones non maillées)

Estimer des densités

  • Densités dans des mailles : rapport d'une quantité sur la surface de référence
  • Intérêt du maillage : normalisation de la surface

Estimer des densités classiques

Estimer des densités classiques

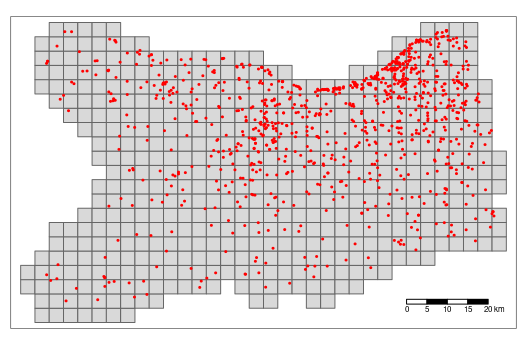
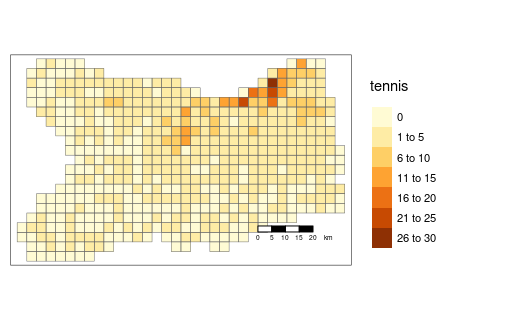
Mailles régulières

Terrains de tennis dans le Calvados

Estimer des densités classiques

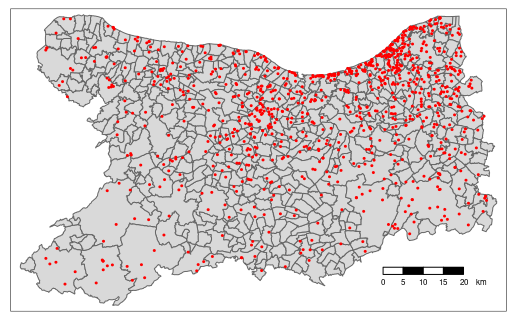
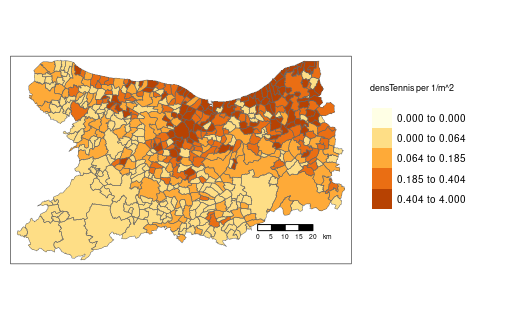
Mailles administratives

Terrains de tennis dans le Calvados

  • Méthode très utile quand on travaille sur des zones non maillées
  • Basée sur un noyau (kernel) de lissage de portée h qu'on estime sur tout l'espace (fenêtre mobile)
  • La pondération est gaussienne, donnant plus de poids aux observations situées proches du centre du noyau

La méthode KDE (kernel density estimation)

La méthode KDE (kernel density estimation)

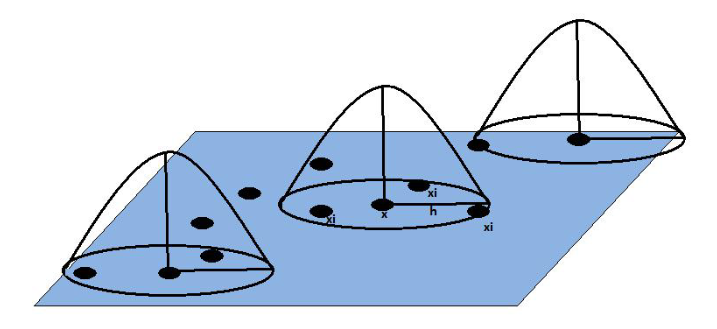
Manuel d'analyse spatiale, INSEE

La méthode KDE (kernel density estimation)

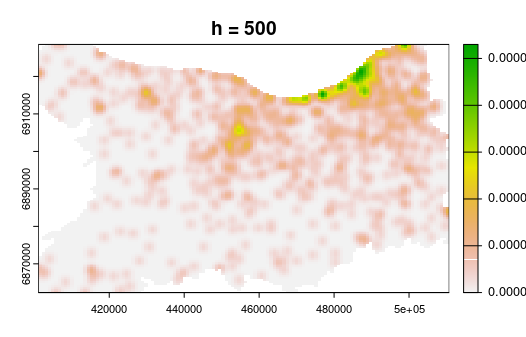
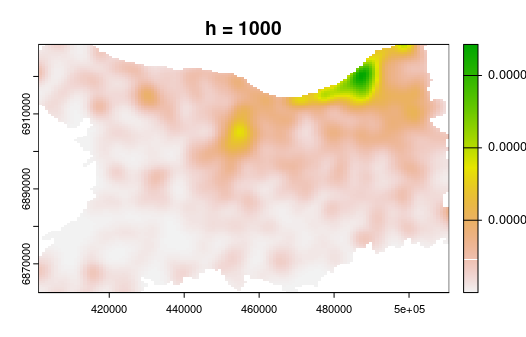
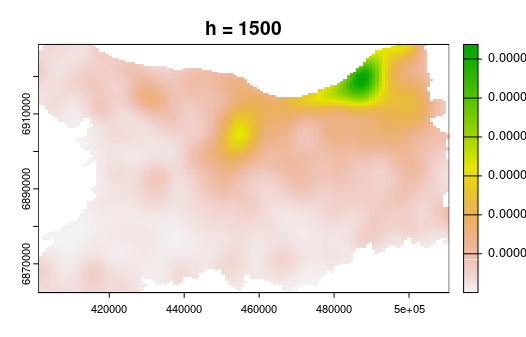
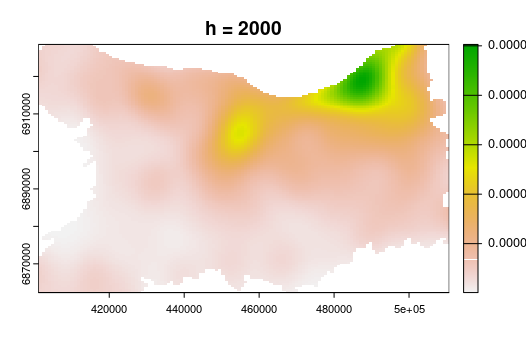
La méthode KDE (kernel density estimation)

La méthode KDE (kernel density estimation)

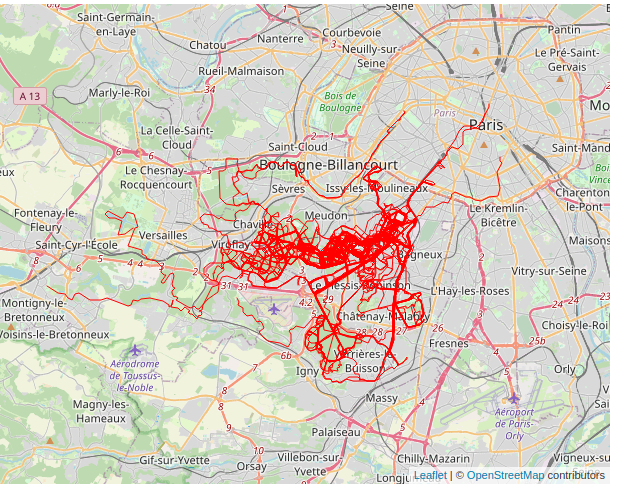
https://tfeuillet.gitpages.huma-num.fr/mapstrava/

  • Biais associé à toutes les méthodes impliquant des fenêtres d'observation
  • Plusieurs solutions :
    • Buffers
    • Correction globale
    • Correction toroïdale

Les effets de bord

Un effet de bord

Manuel d'analyse spatiale, INSEE

  • Il existe des indicateurs pour quantifier la dispersion/agrégation des objets géographiques
  • Il existe trois configurations de points, associées à des processus spécifiques

Mesures d'agrégation et de dispersion

  • Dispersion = répulsion (distribution des transats, des arbres, certains commerces, etc.)
  • Agrégation/concentration = attraction (restaurants, séismes, etc...)
  • Distribution aléatoire = processus CSR (complete spatial randomness)

Mesures d'agrégation et de dispersion

Manuel d'analyse spatiale, INSEE

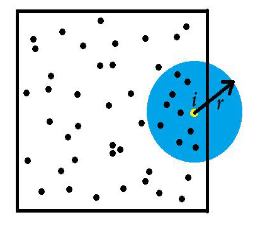
  • L'idée est de calculer la distance moyenne entre chaque point, et de rapporter cette moyenne à la distance attendue en cas de CSR

L'indice NNI (nearest neighbour index)

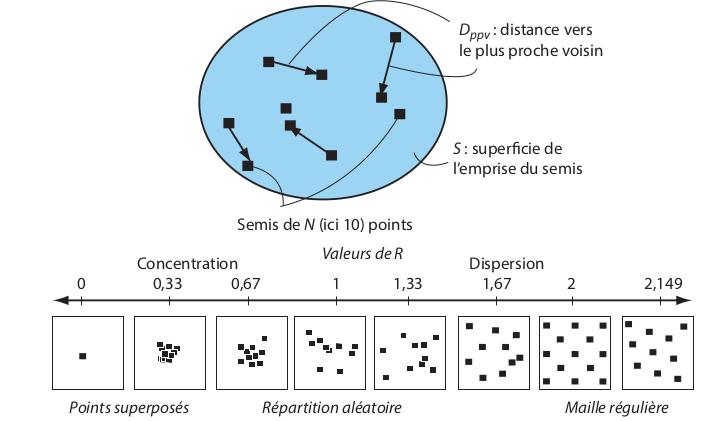
Feuillet et al., 2019, Manuel de géographie quantitative

  • Lissage géographique
  • Interpolation
  • Autocorrélation spatiale
  • Régionalisation

Caractériser les distributions spatiales de valeurs

  • Le lissage géographique a pour but de simplifier les structures spatiales (dans des attributs) pour les rendre plus visibles
  • Il est également basé sur un noyau et une bande passante
  • On cartographie non pas la valeur, mais la valeur moyenne dans le voisinage

Le lissage

Le lissage

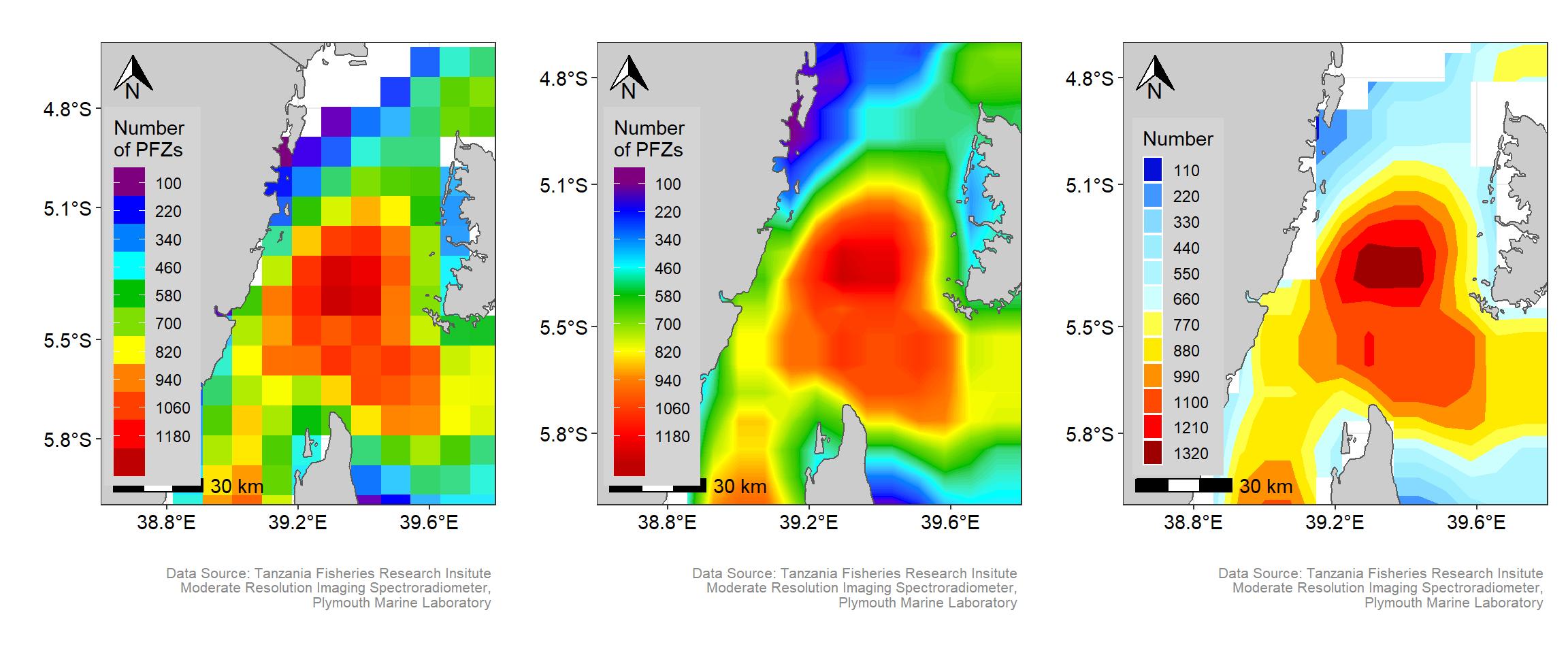
https://semba-blog.netlify.app/06/30/2020/kernel-smoothin-of-spatial-data/

  • Consiste à estimer des valeurs en tout point de l'espace (entre les points)
  • En langage géomatique : passer du vecteur au raster
  • Différent du lissage car données initiales non continues
  • Domaine de la géostatistique

L'interpolation spatiale

  • Ensemble des méthodes mathématiques traitant des données spatiales continues (ie en tout point de l'espace)
  • Née des estimations de gisements miniers dans les années 50 (Danie G. Krige)
  • Principalement basée sur le variogramme et le krigeage

Définition : la géostatistique

Méneroux, 2018, BRGM

  • Pour reconstituer un champ continu d'une variable que l'on sait varier en continu dans l'espace
  • Méthode utilisée principalement en géographie physique (climatologie) : températures, précipitation, rayonnement solaire, etc. et plus généralement en géosciences (ex polluant)
  • Plusieurs méthodes :
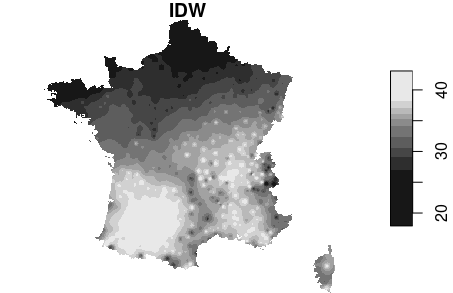
    • IDW (pondération inverse à la distance)
    • TIN (interpolation triangulaire)
    • Krigeage

Pourquoi interpoler ?

  • Méthode basée sur la dépendance spatiale (les voisins les plus proches sont les plus semblables)

La méthode IDW (inverse distance weighting)

Tuto QGIS

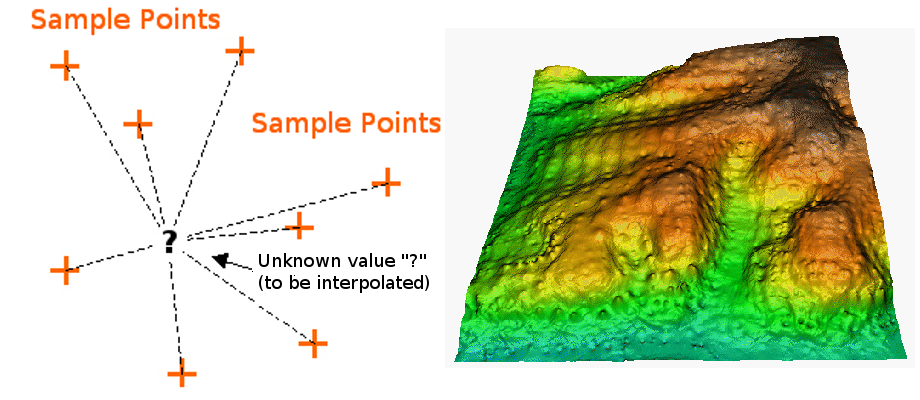
  • Méthode présentant souvent des biais/artefacts

La méthode IDW (inverse distance weighting)

Ressource Arcgis

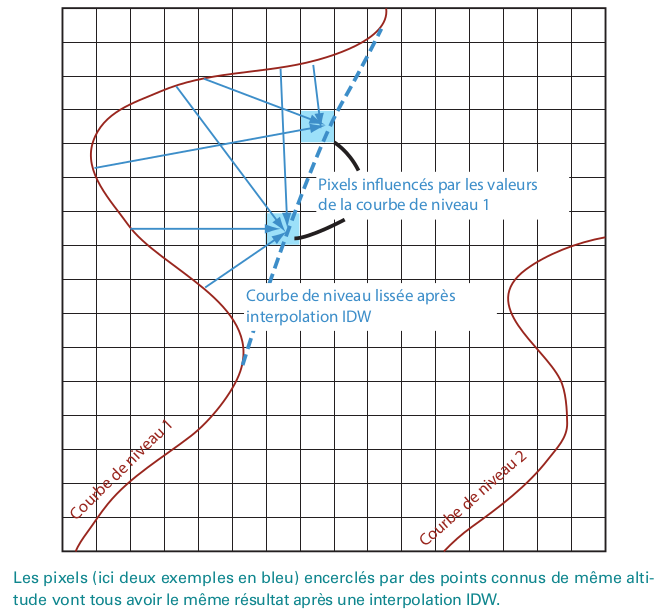
Feuillet et al., 2019, Manuel de géographie quantitative

  • La méthode IDW est une méthode déterministe : il n'y a pas de prise en compte de l'incertitude
  • Pour intégrer l'incertitude, il faut considérer qu'une fonction aléatoire génère la donnée observée (qui est alors une réalisation parmi d'autres possibles)
  • Le krigeage repose donc sur des modèles probabilistes

Le krigeage

  • Les valeurs inconnues vont être estimées en fonction de la distance aux valeurs connues (comme l'IDW) mais aussi en fonction de la structure de l'autocorrélation spatiale
  • Cette structure est analysée à travers la variographie, qui repose sur le variogramme
  • Le variogramme est au coeur de la géostatistique

Le krigeage

  • Le variogramme à une distance h est la demi-moyenne des carrés des différences de Z pour des points distants de h

Le variogramme

\gamma(h)=\frac{1}{2}\mathbf{E}_{|y-x|=h}\left[|Z(x)-Z(y)|^2\right]

Le variogramme

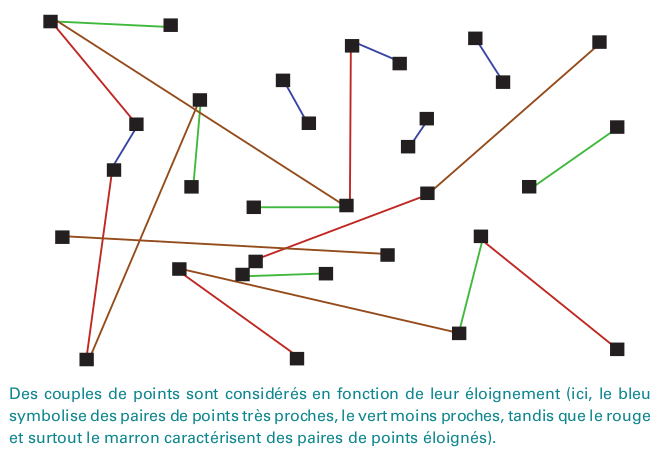
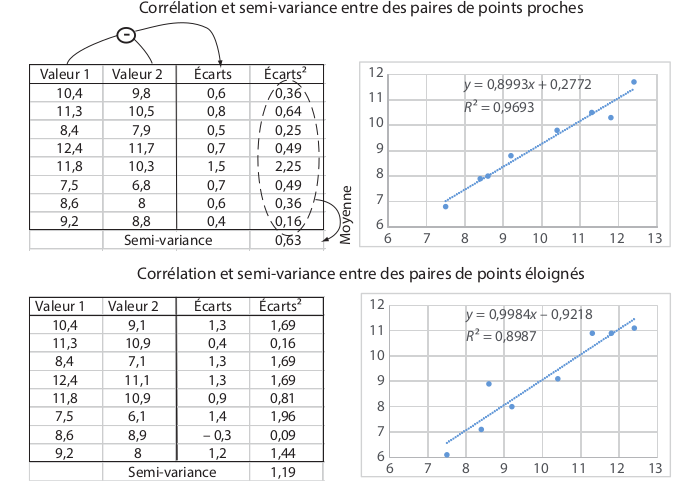
Feuillet et al., 2019, Manuel de géographie quantitative

Tuto ArcGis

Le variogramme

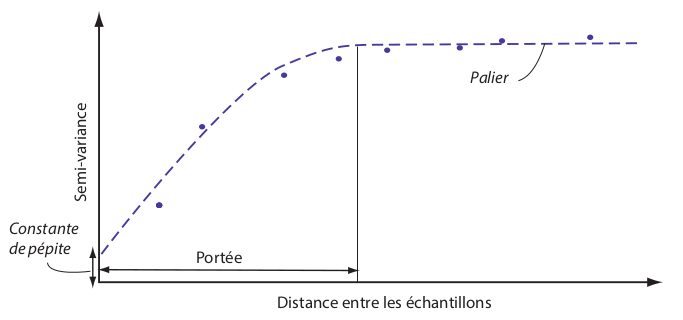
Feuillet et al., 2019, Manuel de géographie quantitative

  • Effet pépite : il y a des différences même pour des observations très proches (pépite n'est pas filon)
  • Palier : Distance à laquelle il n'y a plus d'autocorrélation

Le variogramme

Feuillet et al., 2019, Manuel de géographie quantitative

  • Fort effet de pépite et faible portée : phénomène très variable dans l'espace (pas de structure spatiale) => exemple des filons d'or
  • Absence de palier : données non stationnaires
  • Effet pépite pur : pas de dépendance spatiale
  • Le krigeage comprend plusieurs étapes :
    • Estimer un semi-variogramme empirique
    • Ajuster le modèle au semi-variogramme empirique
    • Appliquer les équations de krigeage pour réaliser les prédictions spatiales
    • Évaluer la qualité de la prédiction

Le krigeage

Les variogrammes théoriques

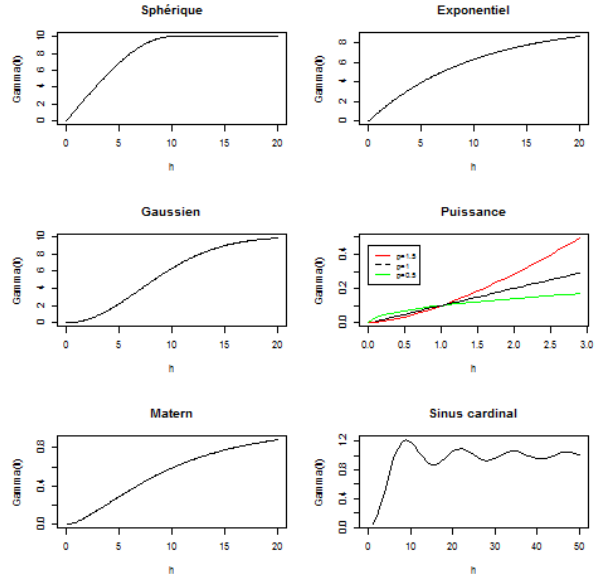
Manuel d'analyse spatiale, INSEE

Estimation de la qualité

  • On divise l'échantillon en un groupe d'entrainement, et un groupe test
  • On fait l'interpolation sur l'entrainement
  • On calcule l'écart entre les estimations et les valeurs du groupe test
  • On utilise pour cela le RMSE (root mean square error)

Exemple

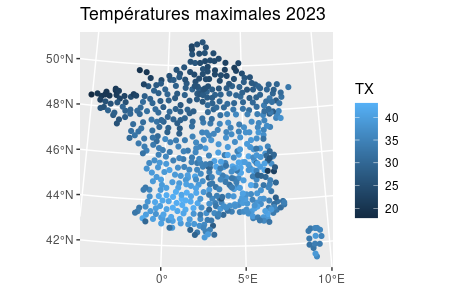
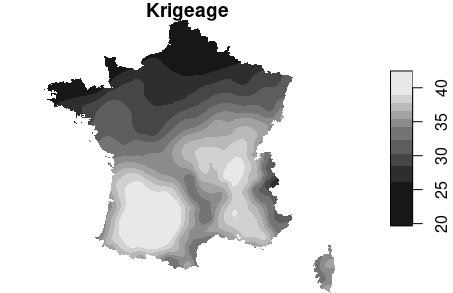
Démonstration sur R

Extension du krigeage ordinaire

  • On peut vouloir utiliser des prédicteurs pour améliorer la prédiction
  • On parle dans ce cas de krigeage universel, ou krigeage par régression
  • L'idée est de réaliser une régression, puis d'ajuster un variogramme sur les résidus de cette régression
  • Le krigeage est donc fait en fonction de la structure spatiale des résidus
  • Cf TD principalement
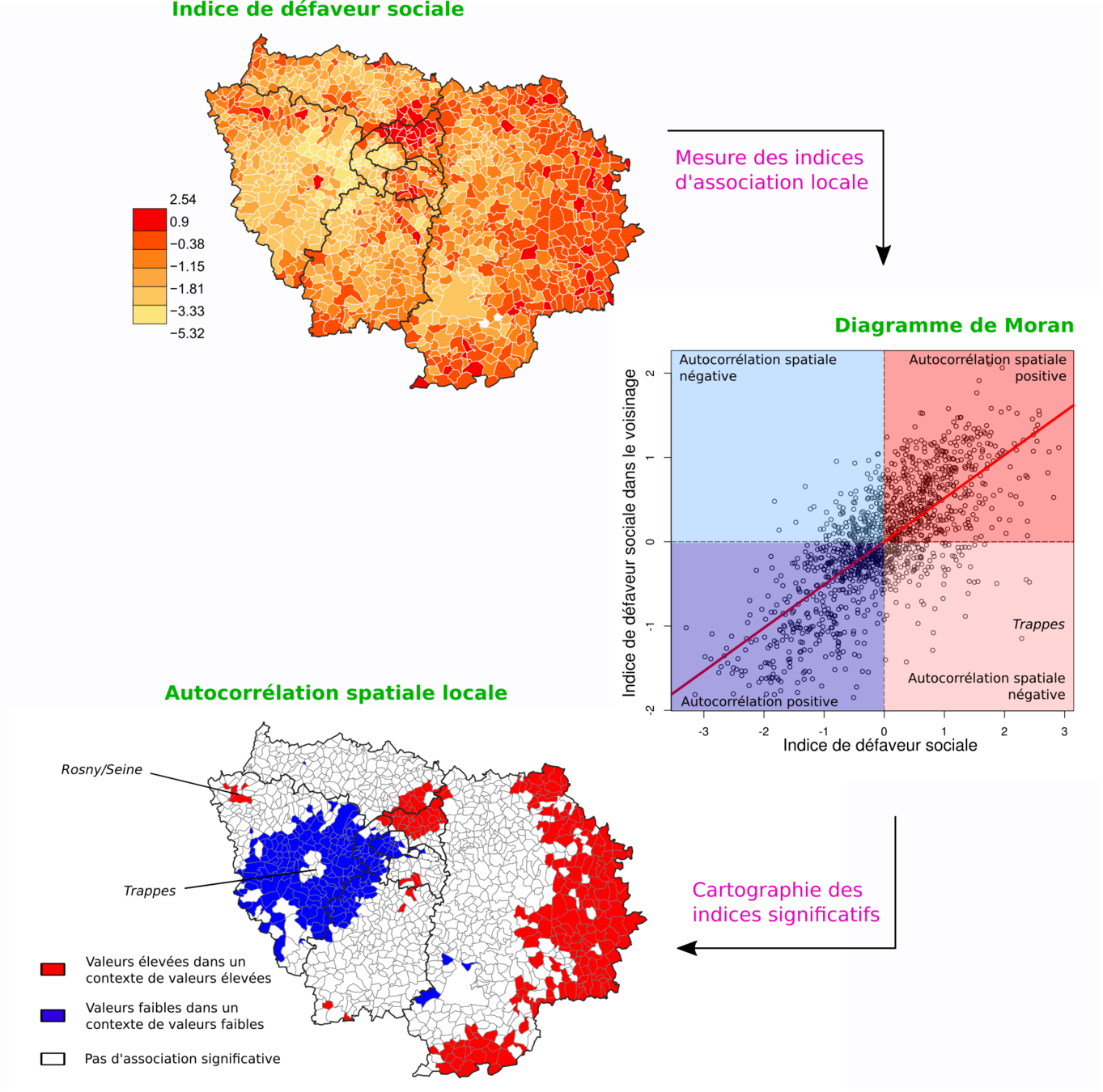
  • Autocorrélation spatiale = corrélation d'une variable avec elle-même
  • Nécessite de définir et éventuellement pondérer le voisinage

Mesurer l'autocorrélation spatiale

Mesurer l'autocorrélation spatiale

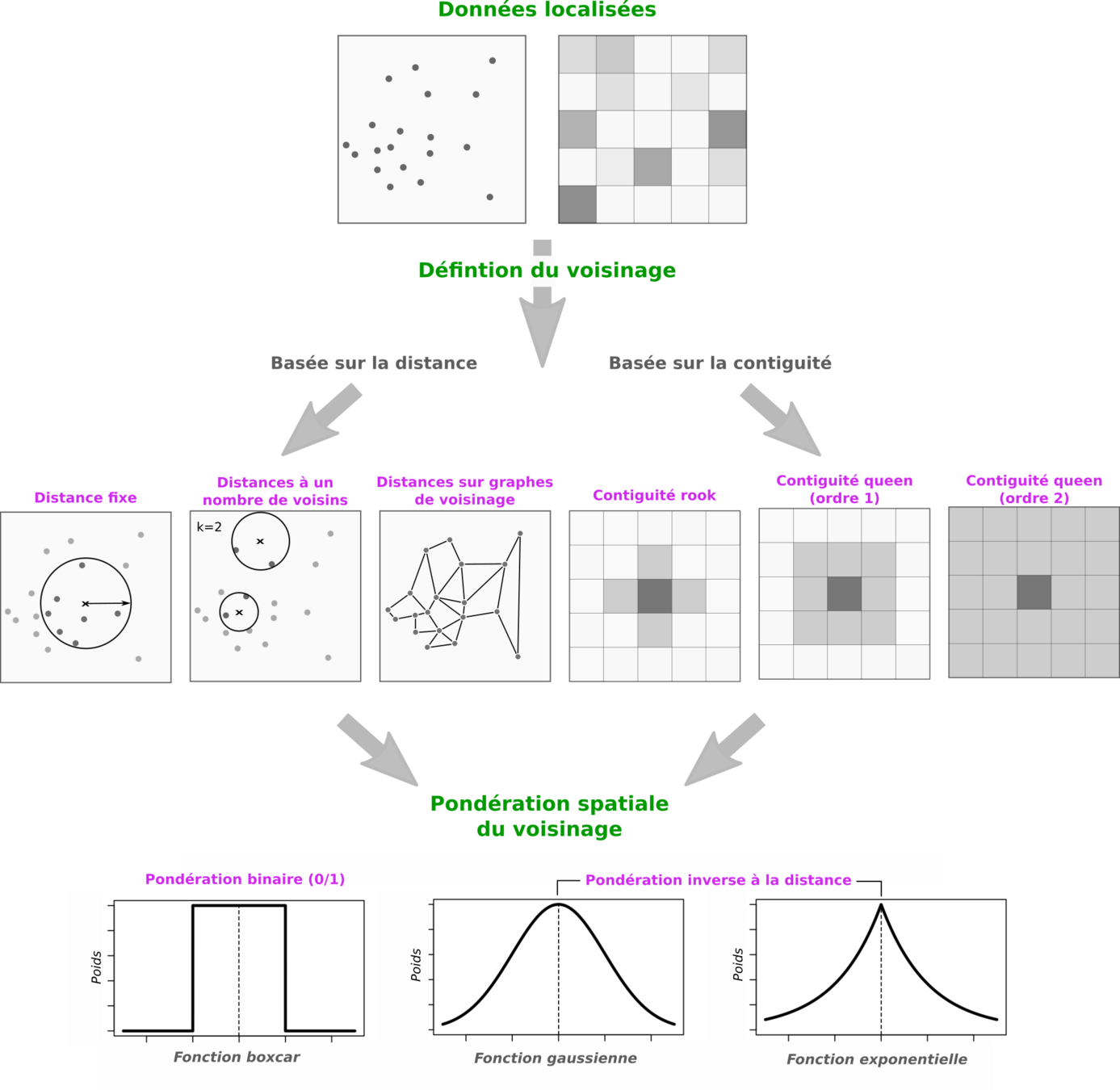
Mesurer l'autocorrélation spatiale

  • La régionalisation consiste à associer des régions/territoires contigus selon leur ressemblance
  • C'est une classification, mais avec une contrainte spatiale

La régionalisation

  • La classification consiste à minimiser la variance intra-classe et maximiser la variance inter-classe

La régionalisation

Lebart et al., 2006

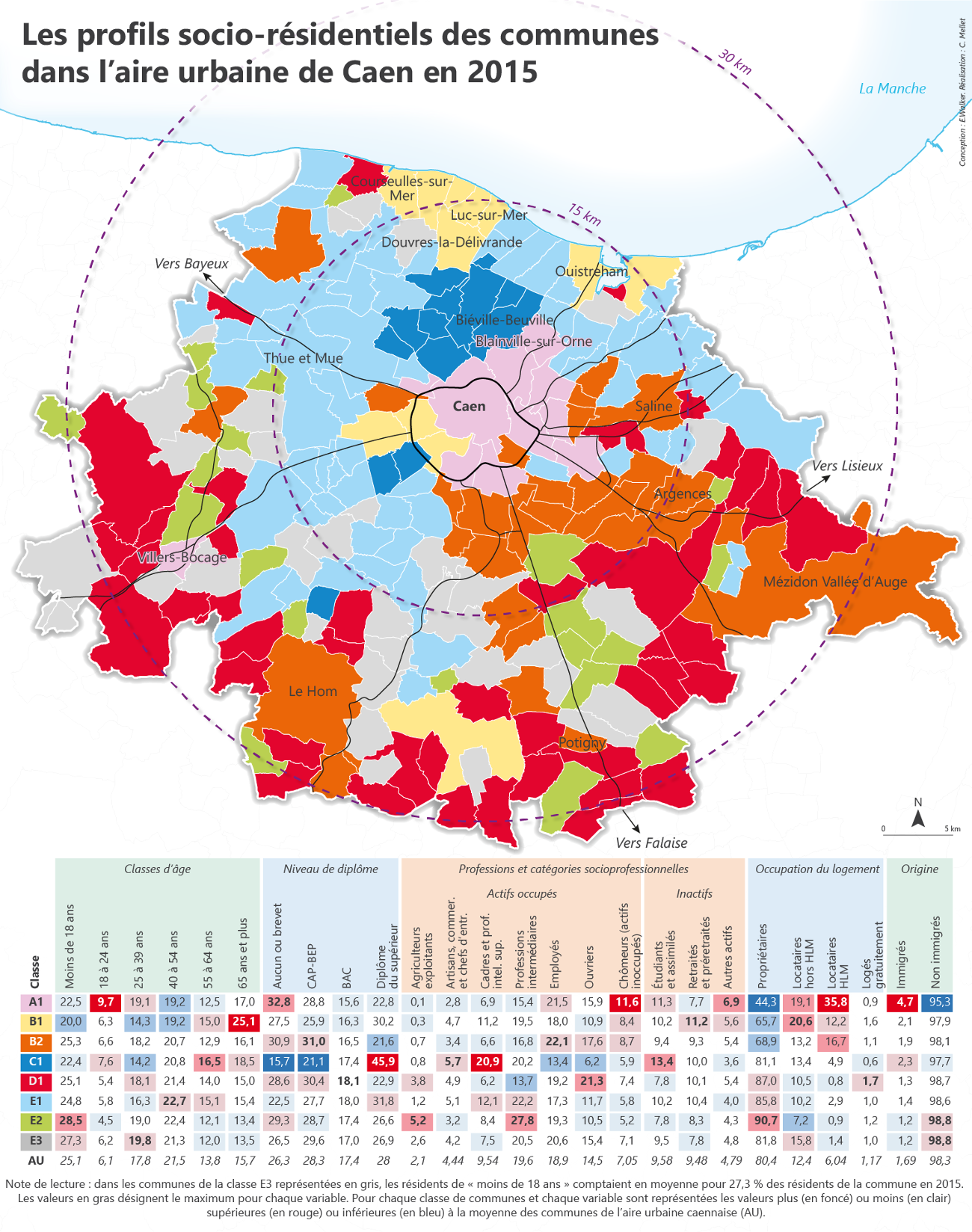
E. Walker, Atlas social de Caen

  • La distance ou la continguité spatiale peuvent être rajoutées dans les calculs

La régionalisation

Feuillet et al., 2019, Manuel de géographie quantitative

3.3. Modéliser les processus sous-jacents

  • Les structures spatiales d'un phénomène peuvent être superposées aux structures du processus explicatif
  • On parle alors de corrélation spatiale
  • On peut modéliser ces relations

Modéliser des corrélations spatiales

  • Pourquoi les corrélations spatiales ne peuvent pas être modélisées par des régressions classiques ?
  • (1) Les données spatiales sont dépendantes dans l'espace
  • (2) Cela signifie que deux observations proches peuvent être quasi identiques
  • (3) Or l'incertitude des coefficients de régression est calculée en fonction du nb d'individus (censés être indépendants)

Modéliser des corrélations spatiales

y = ax + b
Err. Std = s_{\hat{u}} = \sqrt{s_{\hat{u}}^2} \ \ \ \text{où} \ \ \ s_{\hat{u} }^2 = \frac{1}{n-2} \sum_{i = 1}^n \hat{u}^2_i

û = résidus de la régression

Modéliser des corrélations spatiales

  • Cette dépendance spatiale est révélée par la structure spatiale des résidus
  • Si les résidus sont dépendants, la régression est biaisée et il faut recourir à d'autres méthodes

Modéliser des corrélations spatiales

  • llustration

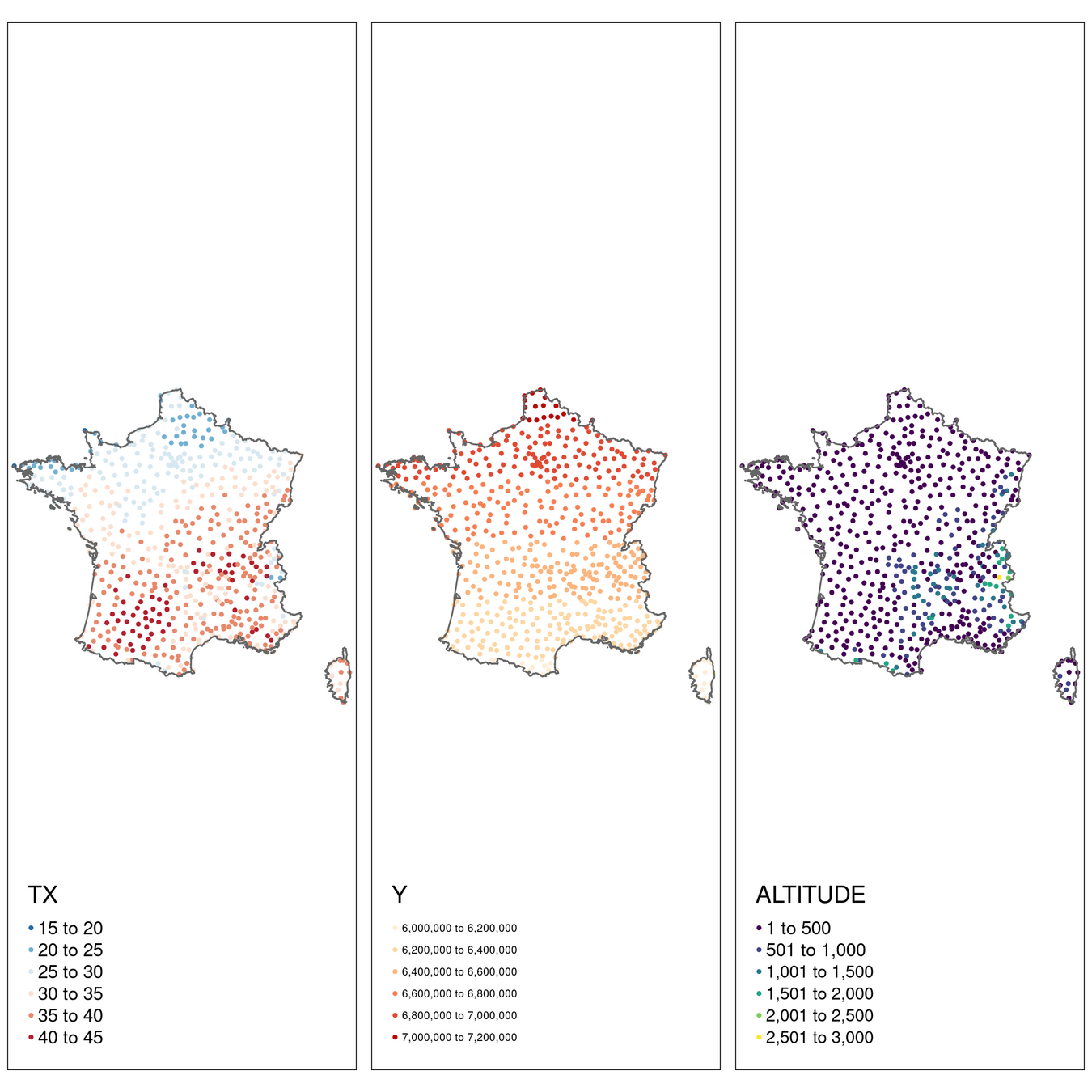
Cartographie des résidus : une étape clé

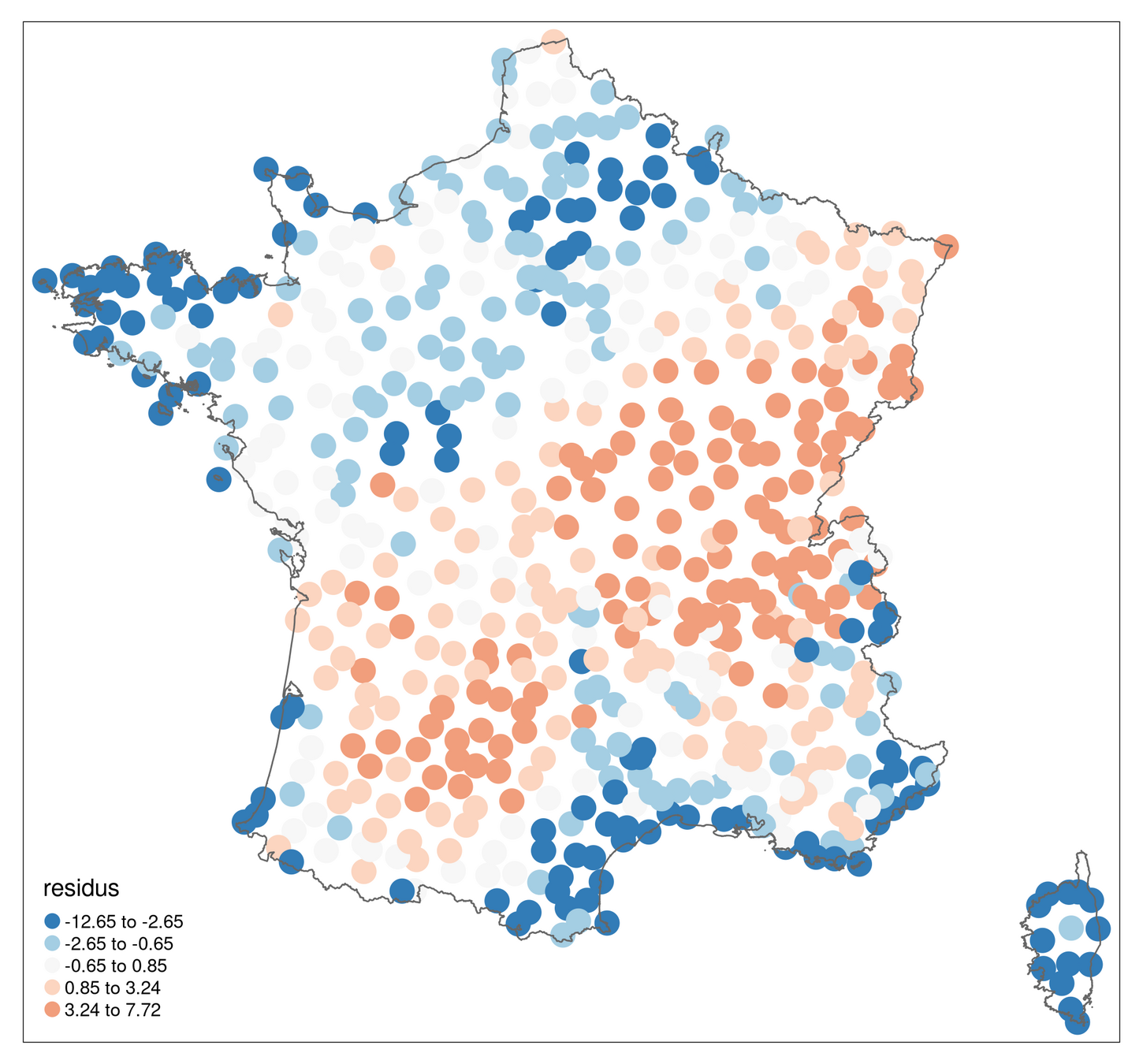
Cartographie des résidus : une étape clé

  • Erreurs de mesure spatialement structurées (biais)
  • Facteurs spatialement structurés inobservés
  • Variable dépendante fortement structurée dans l'espace

Causes possibles de la dépendance des résidus

  • Il existe plusieurs modèles permettant de solutionner la présence de dépendance spatiale dans les résidus
  • Nous présenterons ici 3 de ces solutions

Solutions

  • Il s'agit des modèles GLS (generalized least squares)
  • On modifie les conditions sur les résidus pour préserver des estimations non biaisées

Solution 1 : autoriser la structure spatiale

  • On ajoute des variables spatiales décalées (moyenne du voisinage)
  • On peut faire ça sur Y, sur les résidus ou sur les X
  • Modèles SAR (spatial autoregressive), SEM (spatial error model), SDM (spatial Durbin model)

Solution 2 : les modèles autorégressifs

  • On réalise des régressions locales, autour de chaque observation dans un voisinage donné
  • La principale de ces méthodes est la régression géographiquement pondérée

Solution 3 : les modèles locaux

  • Méthode exploratoire faite pour traiter la non-stationnarité spatiale des relations
  • Elle permet généralement de traiter aussi la dépendance spatiale des résidus

La régression géographiquement pondérée (GWR)

  • Principes :
    1. On définit un voisinage et une pondération
    2. On réalise une régression pour chaque observation sur la base de son voisinage
    3. On obtient une carte de relations

La régression géographiquement pondérée (GWR)

La régression géographiquement pondérée (GWR)

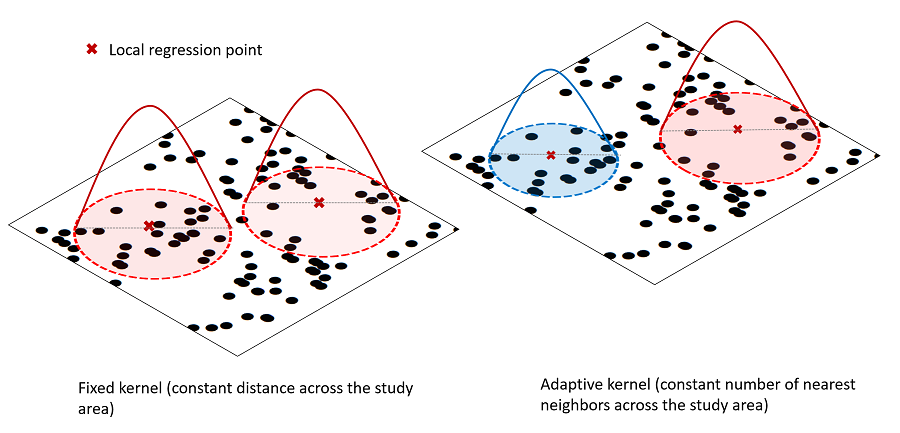
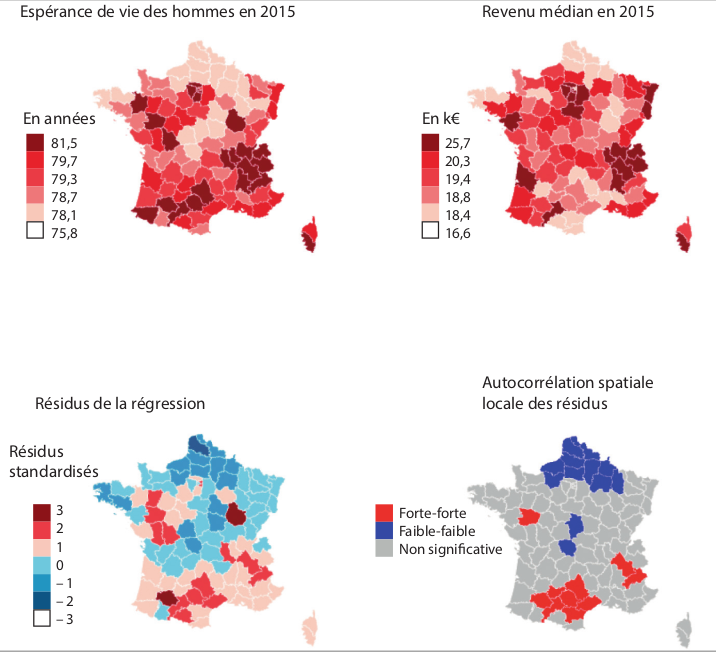
https://gistbok.ucgis.org/bok-topics/geographically-weighted-regression-framework

La régression géographiquement pondérée (GWR)

Feuillet et al., Manuel de géographie quantitative

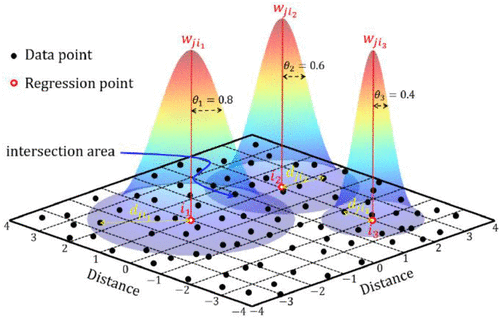
Fang et al., 2021, JSE

La régression géographiquement pondérée (GWR)

Feuillet et al., Manuel de géographie quantitative

Exemples d'applications (GWR)

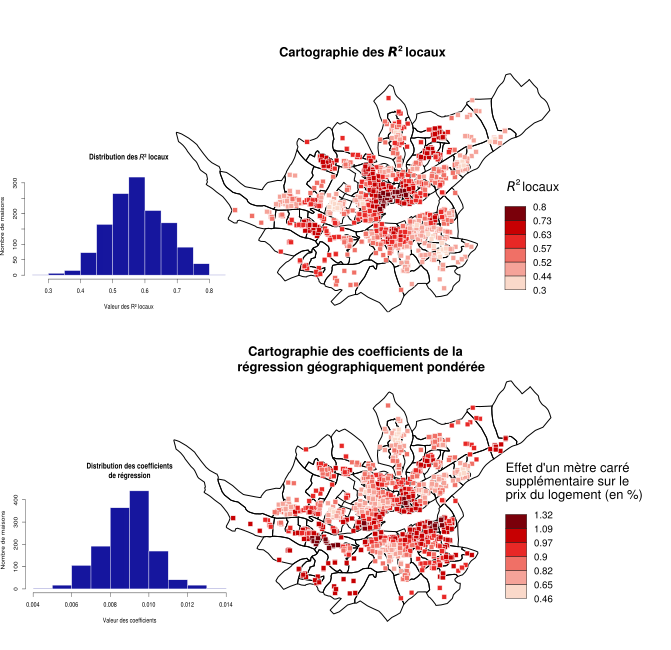
Feuillet et al.,

Manuel de géographie quantitative

Exemples d'applications (GWR)

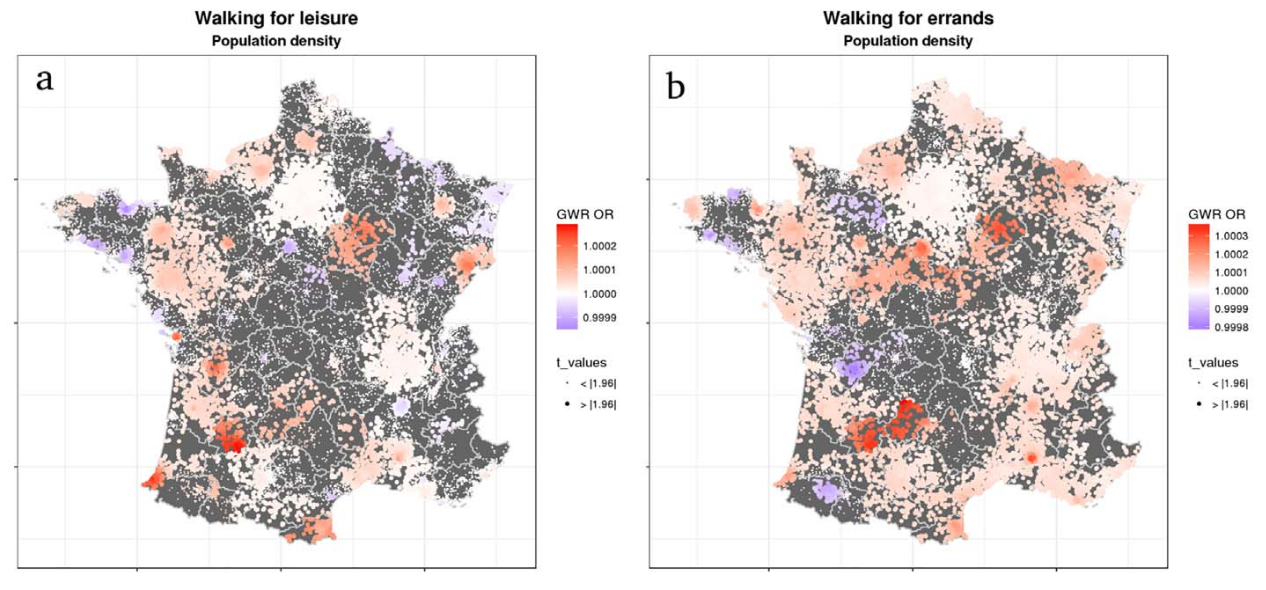
Feuillet et al., 2018, JTG

Exemples d'applications (MGWR)

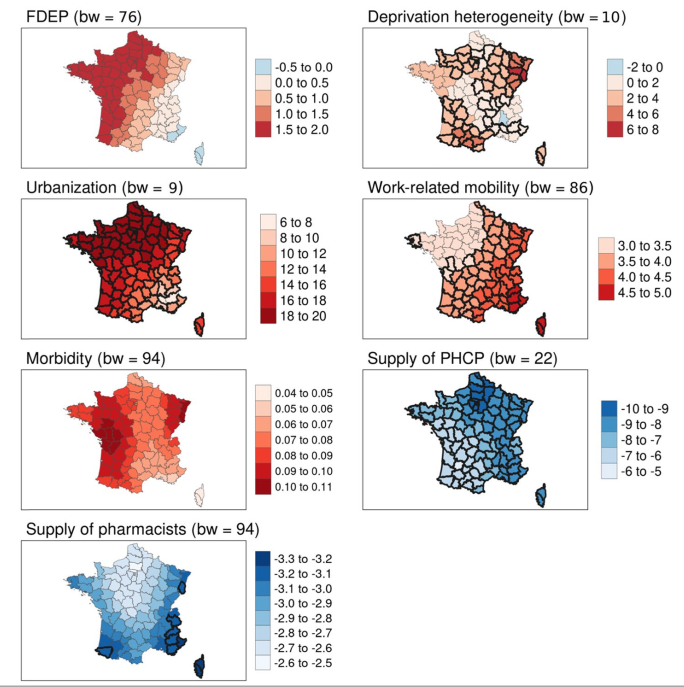
Pilkington et al., 2022, BMC

  • Variation d'échantillonnage
  • Non-linéarité des relations
  • Hétéroscédasticité spatiale
  • Effets de contexte (le plus intéressant)
  • => Cartes GWR souvent difficiles à interpréter

Les causes possibles de la non-stationnarité spatiale

Quand réaliser une GWR ?

Comber et al., 2023

  • Souvent, les données spatiales sont hiérarchiques
  • Les individus vivent dans des quartiers, situés dans des villes, localisées dans des régions, etc.
  • Les modèles multiniveaux permettent de prendre en compte cette structure
  • Des résidus sont estimés à chaque niveau, via une décomposition de la variance

La modélisation multiniveau

La modélisation multiniveau

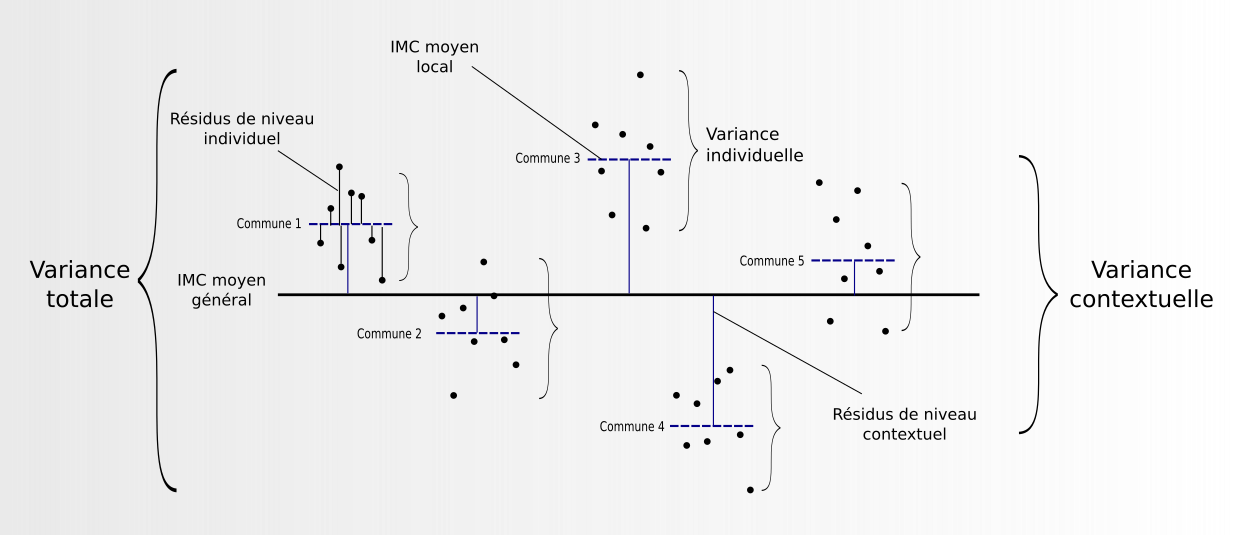
Décomposition de la variance en modélisation multiniveau (Feuillet, 2021)

La modélisation multiniveau

Y_{ij} = b_{0ij} + \varepsilon_{ij}
b_{0j} = b_0 + \zeta_{0j}
Y_{ij} = b_0 + \zeta_{0j} + \varepsilon_{ij}

La modélisation multiniveau

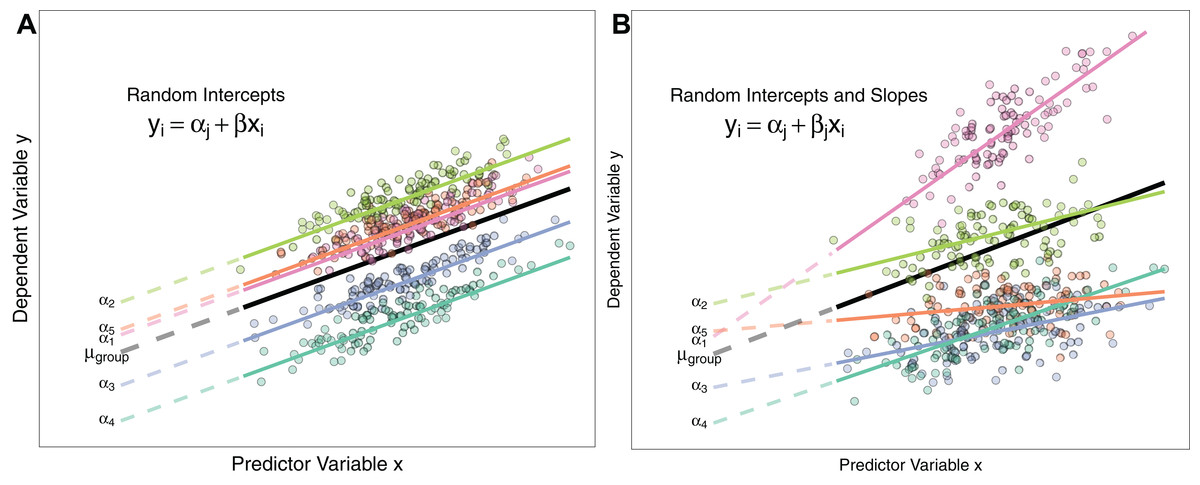
Harrison et al., 2018, PeerJ

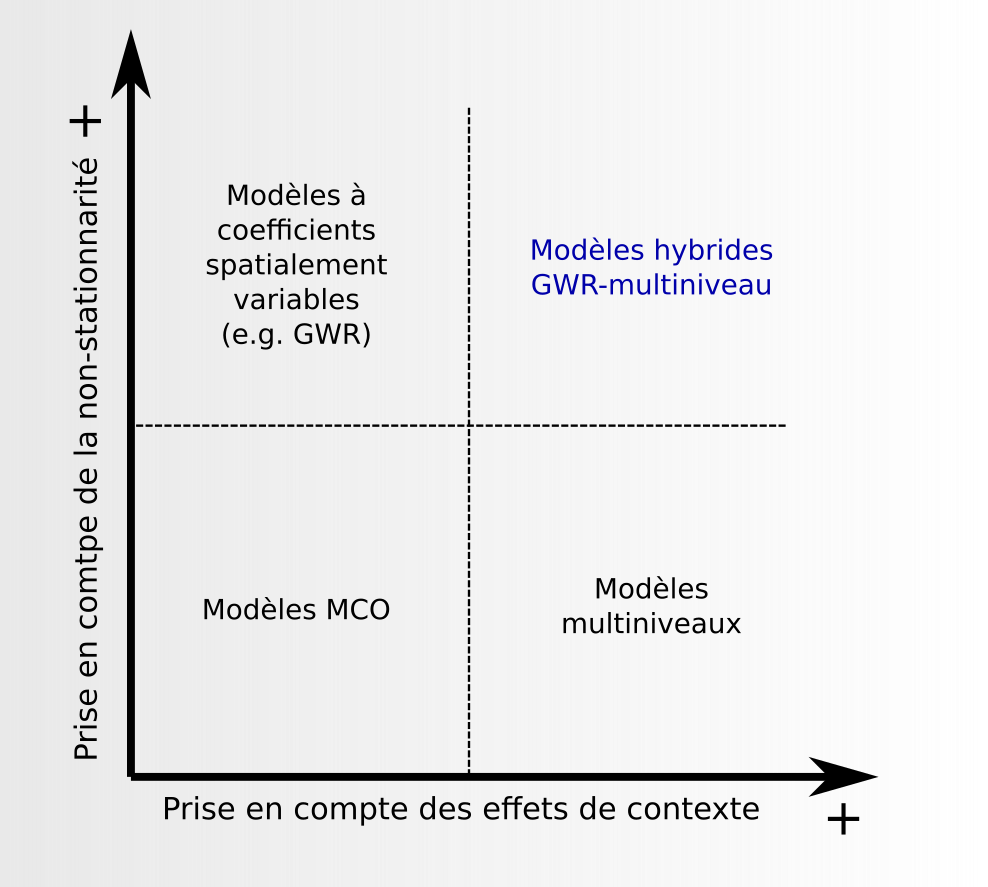
Complémentarité des approches

  • Il existe deux grands types d'outils :
    • Les outils à interface graphique
    • Les outils à interface de programmation (langage informatique)
  • A chaque fois :
    • Outils gratuits/libres (ouverture du code source ou non)
    • Outils propriétaires

4. Les outils de la géographie

  • Logiciels libres :
    • SIG : QGIS, GRASS, SAGA GIS (géosciences) => ponts entre ces logiciels via la boite à traitements
    • Statistiques (spatiales) : GeoDa, jamovi, JASP, etc.

4.1. Les logiciels à interface graphique

  • Logiciels propriétaires :
    • SIG : ArcGIS Pro, MapInfo, Géoconcept, etc.
    • Statistiques (spatiales) : Excel, SPSS, etc.

4.1. Les logiciels à interface graphique

  • Logiciels libres :
    • SIG + stat : R, Python
  • Logiciels propriétaires :
    • SAS, stata, etc.

4.2. Les logiciels à interface de programmation

  • Facilité d’accès aux fonctionnalités du logiciel

  • Utilisés par la majorité des personnes => collaborations facilitées

Intérêts des logiciels à interface graphique

  • Reproductibilité : pour refaire une analyse, il faudra toujours répéter la séquence de clics. Clics en outre difficiles à transmettre aux collègues

  • Gestion des fichiers : accumulation de fichiers intermédiaires rapidement incompréhensibles

  • Domaine : le nombre de boutons/menus est forcément contraint, limitant les domaines de fonctions possibles

Inconvénients des logiciels à interface graphique

5. Exemples d'applications d'analyses spatiales

  • Analyse de semis de points

CM_analyse_spatiale

By tfeuillet

CM_analyse_spatiale

  • 2,349

More from tfeuillet