TD d'analyse spatiale
Calcul d'un indice d'autocorrélation spatiale
Thierry Feuillet - L3 Unicaen - 2025-2026
Lien tuto QGIS pour les nouveaux en SIG : https://tutoqgis.cnrs.fr/index.php
Objectifs du TD
-
Objectif théorique
- Poser une hypothèse théorique et savoir comment la tester
-
Objectif méthodologique
- Comprendre les principes et les limites d'une méthode statistique
-
Objectif technique
- Mettre en oeuvre cette méthode via un outil logiciel
Hypothèse
- Selon la loi de Tobler, les choses proches ont tendance à se ressembler
- En géographie sociale, cela équivaut à une ségrégation socio-spatiale
- Une telle ségrégation existe-t-elle dans le Calvados, au niveau des communes ?
De quoi a-t-on besoin pour tester cette hypothèse ?
- De données caractérisant le niveau socio-économique des communes
- De sélectionner une méthode robuste d'analyse spatialisée de ces données
- D'un outil permettant de mettre en oeuvre cette méthode
Quelles données ?
- Il existe plusieurs variables du recensement de la population qui caractérisent la défaveur sociale à un niveau agrégé :
- Le revenu médian
- Le niveau de diplôme
- La CSP
- Le taux de chômage
- etc.
Le Fdep
(French deprivation index)
- Il s'agit d'un indicateur développé en épidémiologie et validé pour la France
- C'est la première composante principale d'une ACP intégrant les variables suivantes :
- Taux de chômage
- Revenu médian
- Taux d'ouvriers
- Taux de bâcheliers
- Il est calculé aux niveaux IRIS et communes
Le Fdep
(French deprivation index)
- Disponible sur le site de l'INSERM :
https://www.cepidc.inserm.fr/documentation/indicateurs-ecologiques-du-niveau-socio-economique
La méthode
- L'objectif est d'estimer dans quelle mesure des communes ayant des valeurs de Fdep similaires ont tendance à s'agréger spatialement (hotspots ou clusters spatiaux)
- Il s'agit donc d'estimer une éventuelle autocorrélation spatiale sur la base de cette variable
- Si des valeurs similaires s’agrègent, l'autocorrélation spatiale est positive (ségrégation socio-spatiale)
- Si des valeurs fortes s'agrègent à des valeurs faibles, l'autocorrélation spatiale est négative
- Si c'est aléatoire, il n'y a pas d'autocorrélation
La méthode
- Il existe plusieurs indicateurs d'autocorrélation spatiale
- Ce sont des statistiques qui permettent d'affirmer ou non la présence d'autocorrélation
- Il en existe deux principaux :
- L'indice I de Moran
- L'indice C de Geary
- Et leurs variantes locales (LISA - local indicators of spatial association)
L'indice I de Moran
- Pour chaque observation localisée, on compare la valeur de la variable étudiée (i) aux valeurs voisines (j)
- Si les valeurs voisines sont en moyenne plus proches de i que la moyenne de toutes les valeurs, alors il y a autocorrélation spatiale
- Pour mettre en œuvre cette méthode, il est nécessaire de définir deux éléments :
- Le voisinage
- Le poids éventuel à lui donner
Définition du voisinage
- On peut définir un voisinage de différentes façons, selon l'étude et la nature des données (points ou polygones) :
- Par la distance (euclidienne ou réseau)
- Par la contiguïté spatiale (différents ordres)
- Par un nombre de voisins les plus proches (équivalent à une distance)
Définition du voisinage
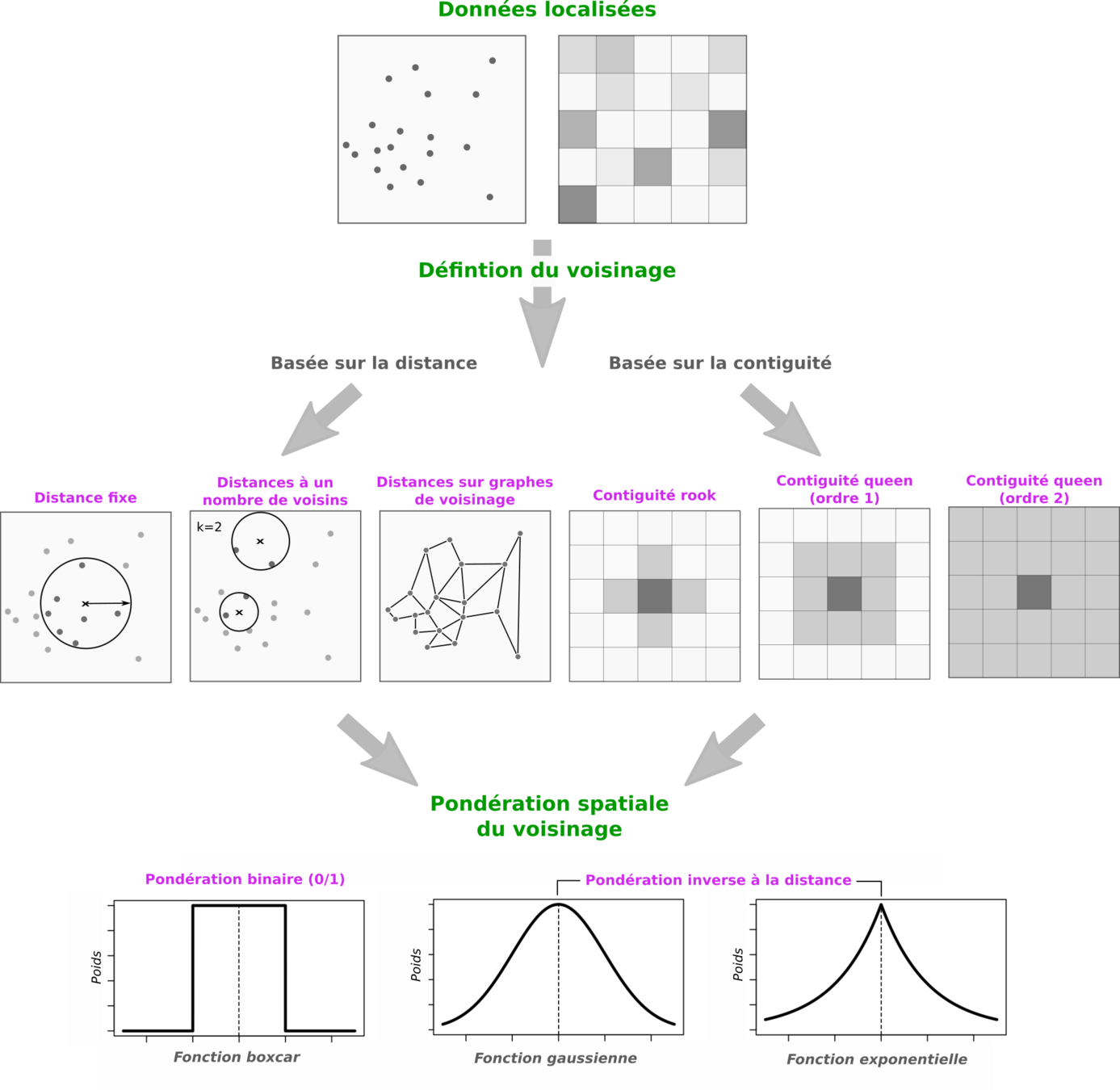
Manuel de géographie quantitative (Feuillet et al., 2019)
Définition du poids
- On peut décider que chaque voisin a un poids identique (1 si voisin, 0 sinon)
- Ou bien souhaiter que ce poids dépende de la distance à i
- On va alors pondérer spatialement le voisinage

Manuel de géographie quantitative (Feuillet et al., 2019)
Le principe de la méthode
- On définit le voisinage
- On lui attribue éventuellement un poids
- On calcule un tableau à deux colonnes :
- une colonne avec la valeur en i
- une colonne avec la valeur moyenne du voisinage
- On réalise une régression linéaire sur ces coordonnées
- => Le nuage de points correspond au diagramme de Moran
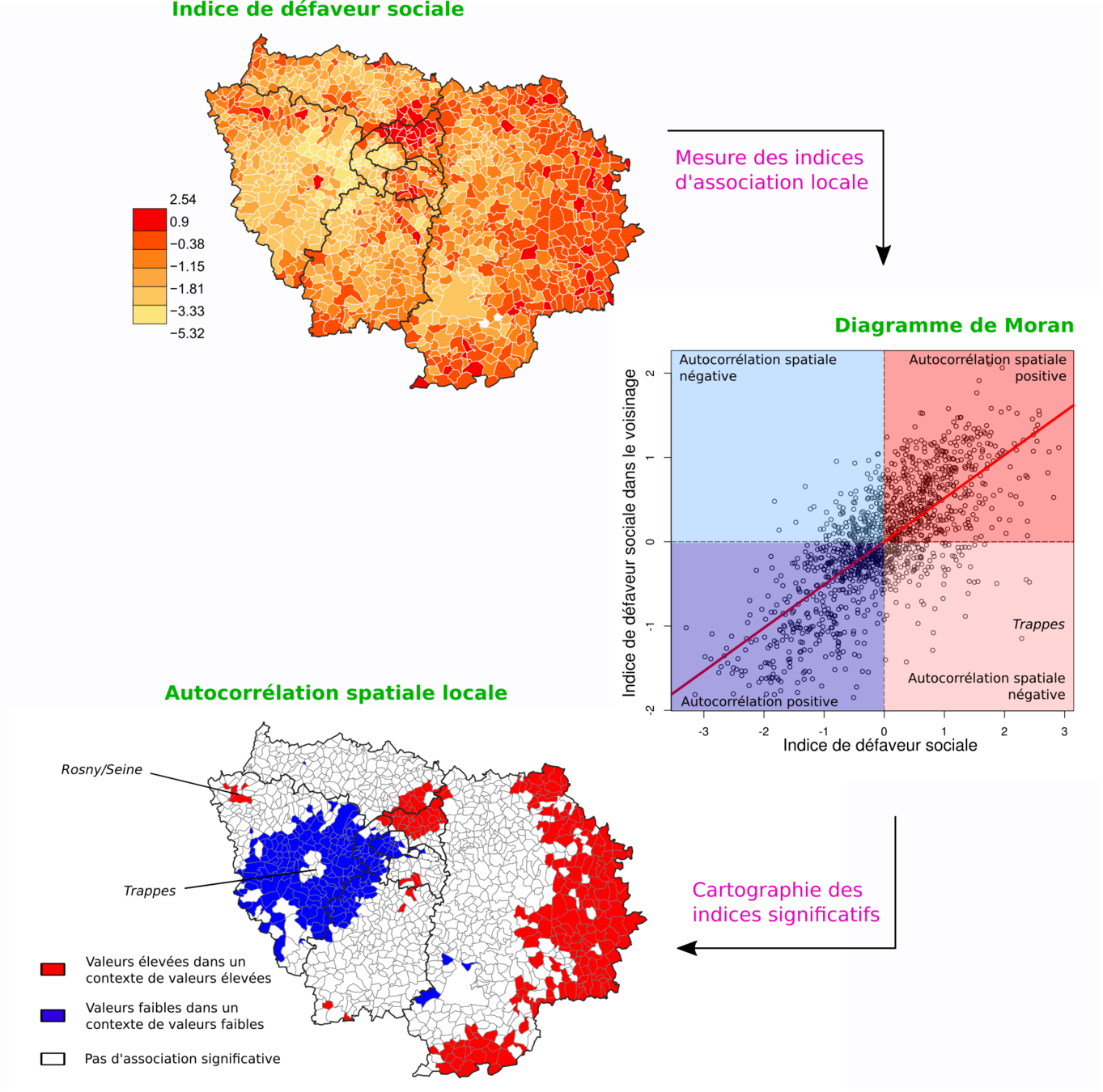
Manuel de géographie quantitative (Feuillet et al., 2019)

Manuel de géographie quantitative (Feuillet et al., 2019)

- Le coefficient directeur de la droite de régression correspond à l'indice de Moran
- Plus il est proche de 1 ou -1, plus l'autocorrélation est forte
- S'il est proche de 0, la droite est horizontale et il n'y a donc pas de relation entre les valeurs et les valeurs voisines (aléatoire)
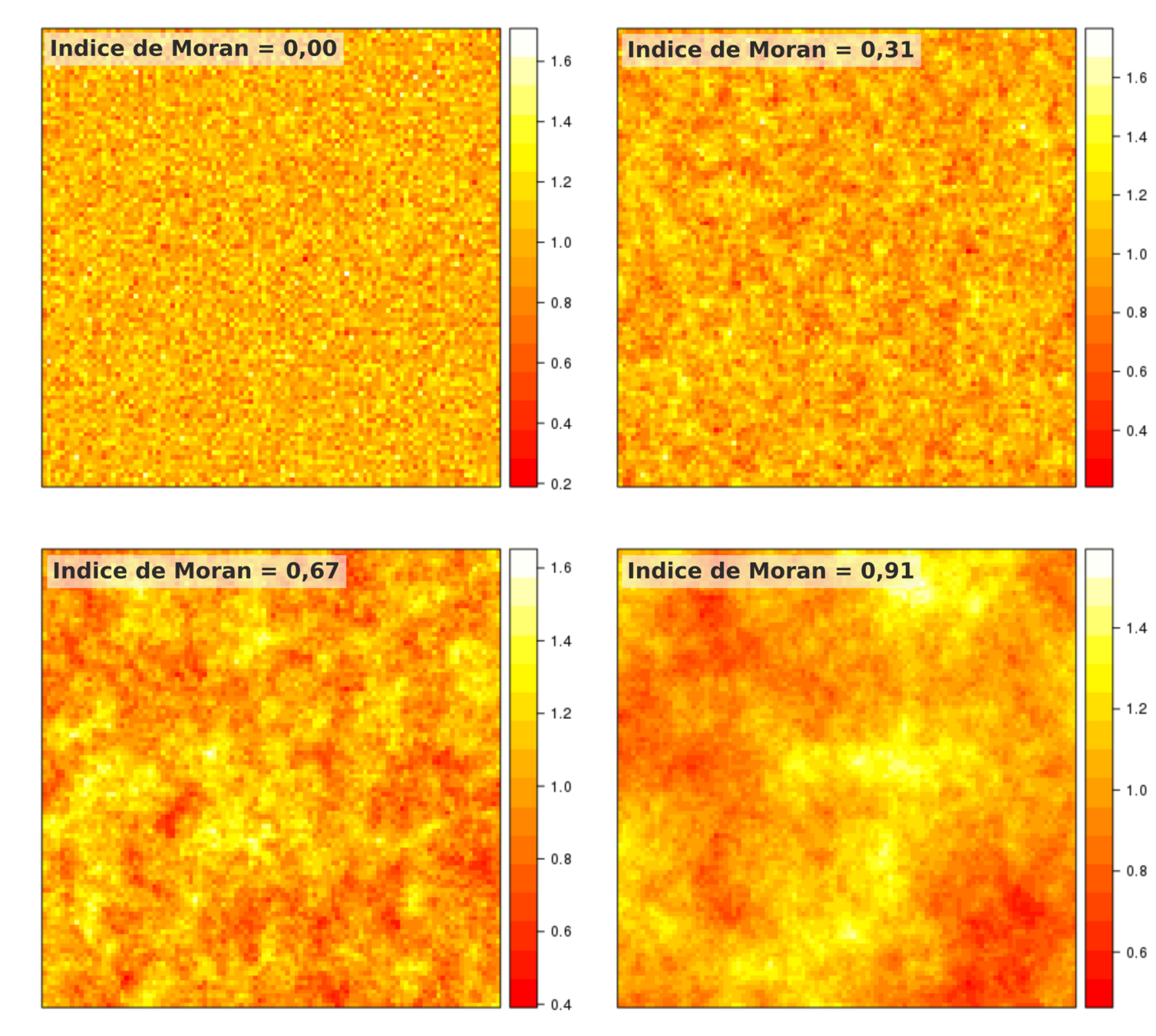
Illustration de différentes valeurs d'indices
Manuel de géographie quantitative (Feuillet et al., 2019)
Equation de l'indice
Test de l'indice
- Il faut tester la valeur de l'indice pour être certain que l'autocorrélation est significative et non due à la fluctuation d'échantillonnage
- L'hypothèse nulle du test est la distribution aléatoire des valeurs, et l'hypothèse alternative est donc leur caractère regroupé
- On utilisera une approche computationnelle basée sur les permutations
Test de l'indice
- Le principe est simple : on mélange x fois les valeurs de l'échantillon de façon aléatoire, et on calcule l'indice de Moran à chaque fois
- On obtient une distribution théorique sous l'hypothèse nulle (aléatoire)
- Si le "vrai" indice I est en queue de distribution, alors on rejette H0
- Plus précisément, la pseudo p-value égale :
où R est le nombre de fois où l'indice est > ou = à l'indice réel, et M le nombre permutations
Indice local de Moran (LISA)
- Nous avons calculé une valeur d'indice pour chaque observation, avec la formule suivante :
- La moyenne de ces indices locaux équivaut à l'indice global
- Chaque indice local peut être testé avec des permutations selon le même principe que précédemment
- On aboutit à une carte mettant en valeur d'éventuels clusters spatiaux

Manuel de géographie quantitative (Feuillet et al., 2019)
Indice local de Moran (LISA)
Objectif du TD
- Construire le diagramme de Moran
- Calculer l'indice global de Moran et le tester
- Calculer les indices locaux, les tester et les cartographier
- Rendre un document illustré (graphiques et cartes) restituant et analysant l'hypothèse, la procédure méthodologique (données et méthodes) et les résultats (discutés)
Mise en œuvre de la méthode
- Il existe plusieurs outils permettant de mettre en œuvre ces calculs
- Soit par langage de programmation (par exemple R ou Python)
- Soit avec des logiciels à interface graphique, payant (par exemple ArcPro) ou libre (par exemple Geoda)
- Nous allons ici utiliser Geoda
Chaîne de traitements et d'analyses
- Prise en main du logiciel
- Acquisition de la donnée
- Préparation de la donnée (géotraitements)
- Calcul des matrices de voisinage et de pondération spatiale
- Calcul des indices
- Analyse de sensibilité et discussion des résultats
- Restitution
1. Prise en main du logiciel
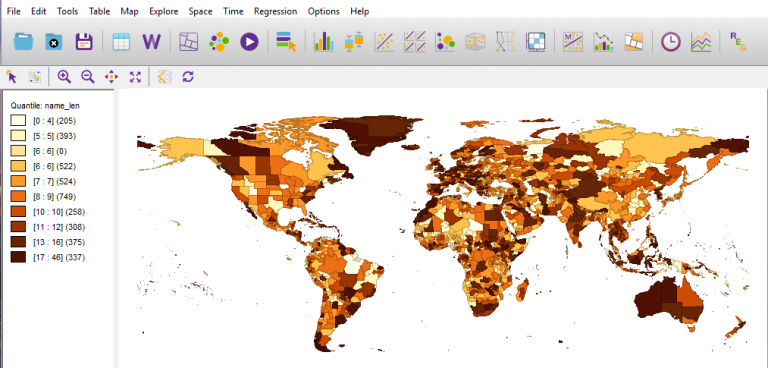
2. Acquisition des données
Le Fdep est disponible sur le catalogue atlas santé en format spatial : https://catalogue.atlasante.fr/
3. Préparation des données
Identifier les problèmes potentiels (topologie, données aberrantes, etc.) puis les corriger
4. Matrices de voisinage et poids
- Tools > Weights Manager
- Testez différents schémas de voisinage (contiguïté, distance, knn) et observez les graphes de voisinage
TD_analyse_spatiale
By tfeuillet
TD_analyse_spatiale
- 2,526



