Technical Interviews
By ACM
Getting the Interview
The Usual
- Resume
- Companies love to see previous internships
- If you don't have any, put projects and any experience close to an internship
- Leadership roles/involvement in clubs is helpful
- Applying
- Apply everywhere, don't worry about being unqualified, you always have next year
- Skills
- Make sure you can talk about skills you list on your resume
Other important things
- "Networking"
- This just means having friends, ask upperclassmen friends or old intern friends for referrals or recruiter details
- Sometimes you need to push HR a bit
- If you've got deadlines and a company hasn't responded after an interview it can be worth it to send a couple emails
- Put your projects on Github
- Also, I'd say try have some unique side projects. Everyone made a basic Node web app, there are less flashy but more interesting projects out there
What is a technical interview
- Generally 1-3 programming problems
- Problems are often algorithm focused
- Supposed to show how the candidate thinks
Format
- Sometimes the interviewer might ask a few general/resume questions first
- Interviewer gives 1-3 programming problems
- Interviewer asks if the candidate has any questions
- Try to ask a couple of questions here, about company culture, average day, etc.
What companies look for
- Communication
- Solving the problem correctly
- Thought process
(Disclaimer, we aren't recruiters and don't know how companies make decisons)
Communication
- Discuss how you plan to solve the problem
- Talk about your thought process while coding
- Let the interviewer know if you need to take some time to think about the problem
Try do mock interviews with friends (or ACM) to help practice this
Solving the problem
- Practice interview problems
- Try practice without a computer sometimes
- Resources
- Leetcode.com
- Hackerrank.com
- Cracking the Coding Interview
- ACM workshops
- CLRS, Skiena Textbooks (Advanced)
- Practice problems later
Thought process
- Companies say this is the most important part
- How do you approach the problem?
- Do you consider which data structures to use
- Do you consider edge cases
- Do you consider time complexity
- Do you create test cases and test your solution?
- Do you try check if there could be a better approach?
Some tips
- Practice
- Try do mock interviews with friends or mentors
- If that isn't possible try solve the problem on paper
- Take the interviewers hints
- Plan out your solution before coding
- Don't chase a solution you've seen but can't remember
- Test your code
General Precurser
- Time complexities
- Data structures
Time Complexities
- O(n) =>
- O(n^2) =>
- Basic time complexities included below
for(int i = 0; i < arr.size(); i++)for(int i = 0; i < arr.size(); i++)
for(int j = 0; j < arr.size(); j++)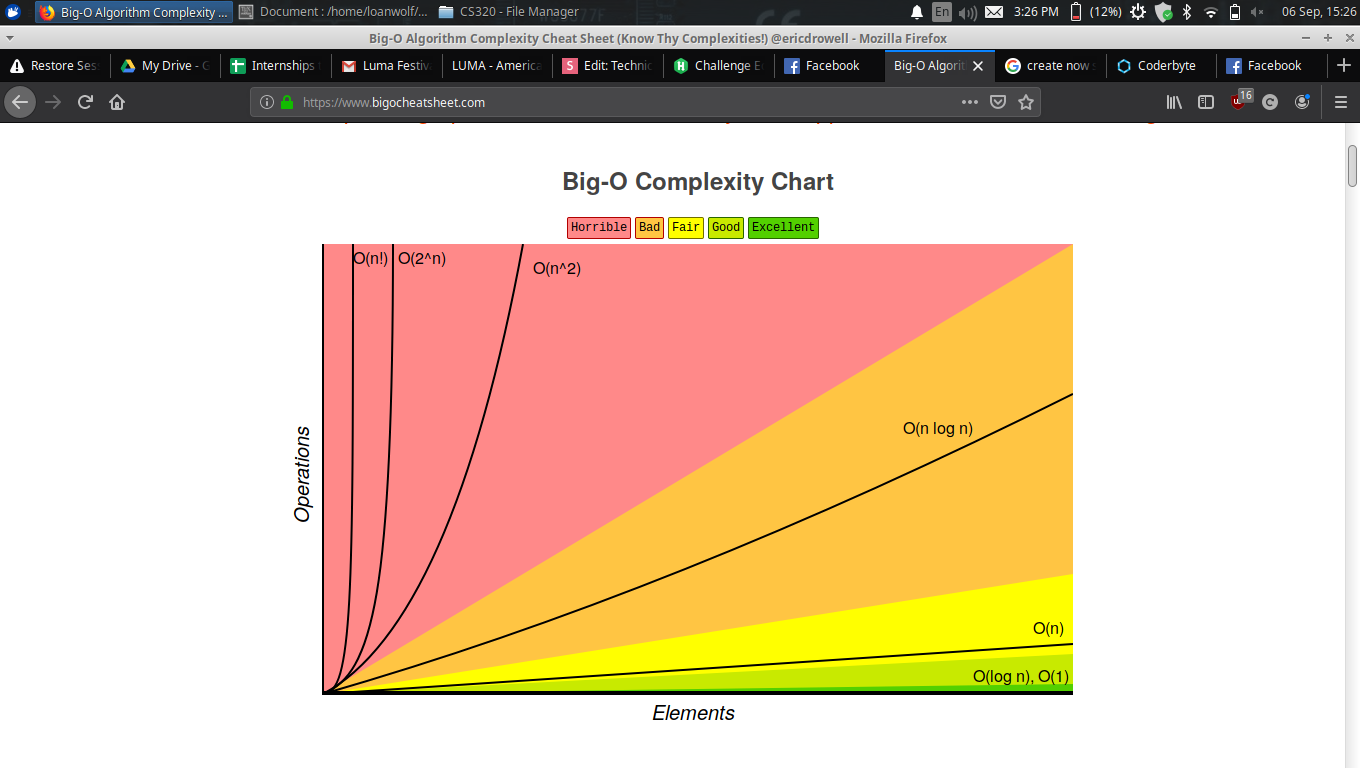
Data Structures
- Arrays
- Hash Maps/Sets
- Binary Trees
- Stacks
- Queues
Problem #1
2 Sum
2 Sum
- Leetcode: https://leetcode.com/problems/two-sum/
- Given a list of integers and a value (v), return a list containing the 2 indices that sum to v.
- Ex: S = 7, list = [1, 2, 3, 4, 8, 11, 0].
- We would return [2, 3] because 3 and 4 sum to 7.
Naive Solution
- This solution is O(n^2), but are we repeating any work?
- We are checking if i + j = S, can we change something so that we repeat work?
Text
def twoSum(arr, S):
sums = []
for i in range(0, len(arr)):
for j in range(i+1, len(arr)):
# Here we are only looking for a single pair,
# so we can return after we find it.
if (arr[i] + arr[j] == S):
sums.append(arr[i])
sums.append(arr[j])
return sums;
return NoneO(n) Solution
Text
def twoSum(arr, S):
sums = []
hashTable = {}
for i in range(0, len(arr)):
sumMinusElement = S - arr[i]
# Lets check if we have seen S - arr[i] before. If so, then we have a pair.
if sumMinusElement in hashTable:
sums.append(arr[i])
sums.append(sumMinusElement)
return sums
# Lets put arr[i] in the hash table so that if we get anther value j such
# that arr[j] + arr[i] = s, we check if we have seen arr[i] in O(1).
hashTable[arr[i]] = arr[i]
return NoneProblem #2
Coin Change
Coin Change
- Leetcode: https://leetcode.com/problems/coin-change/
- Given a list of coins, determine the fewest number that can be used to create a target value
Considerations
- What algorithm can we use
- How fast is it
- Does it work in every case
Idea #1
- Greedy algorithm
- Take the biggest coin every time
- Does this always work?
- Test cases
- [1, 5, 10, 25], 18
- Answer: 5
- [1, 6, 7, 15], 12
- Answer: 2
- [1, 5, 10, 25], 18
Idea #2
- Try every combination
- Basically guaranteed to work
- How fast is this?
- Exponential complexity
Idea #2 Implementation
class Solution:
def coinChange(self, coins: List[int], amount: int) -> int:
#base cases
if amount == 0:
return 0
if amount <= 0:
return float('inf')
best = float('inf')
for c in coins:
best = min(best, self.coinChange(coins, amount-c))
#deal with some edge cases
if best == float('inf'):
return -1
if best == -1:
return best
return best+1Idea #3
Dynamic Programming
What is dynamic programming
Two main requirements
- Overlapping sub-problems
- Optimal substructure
- This means that sub-problems can be combined to solve the main problem
Why do we care
- Can often bring time complexity down from exponential to linear on difficult problems
- Commonly asked category in harder interviews
How does this apply to coin change
- Example: [3,5,7], 16
- With our brute force solution the functions calls will look like this:
16
9
11
13
4
6
2
6
4
8
8
6
10
Idea #3 Solution
class Solution:
def coinChangeH(self, coins: List[int], amount: int) -> int:
if amount in self.seen:
return self.seen[amount]
if amount == 0:
return 0
if amount <= 0:
return float('inf')
best = float('inf')
for c in coins:
best = min(best, self.coinChangeH(coins, amount-c))
if best == float('inf'):
self.seen[amount] = float('inf')
return float('inf')
self.seen[amount] = best+1
return best+1
def coinChange(self, coins: List[int], amount: int) -> int:
self.seen = {}
res = self.coinChangeH(coins, amount)
if res == float('inf'):
return -1
return res-
Some leetcode weirdness requires initializing seen in the main coinChange rather than making it global/member var
-
Need to make sure to cache results of the failiures too
Problem #3
Binary Tree Level Order Traversal
Traversing Trees
- Depth First Search
- Pre-order
- In-order
- Post-order
- Breadth First Search
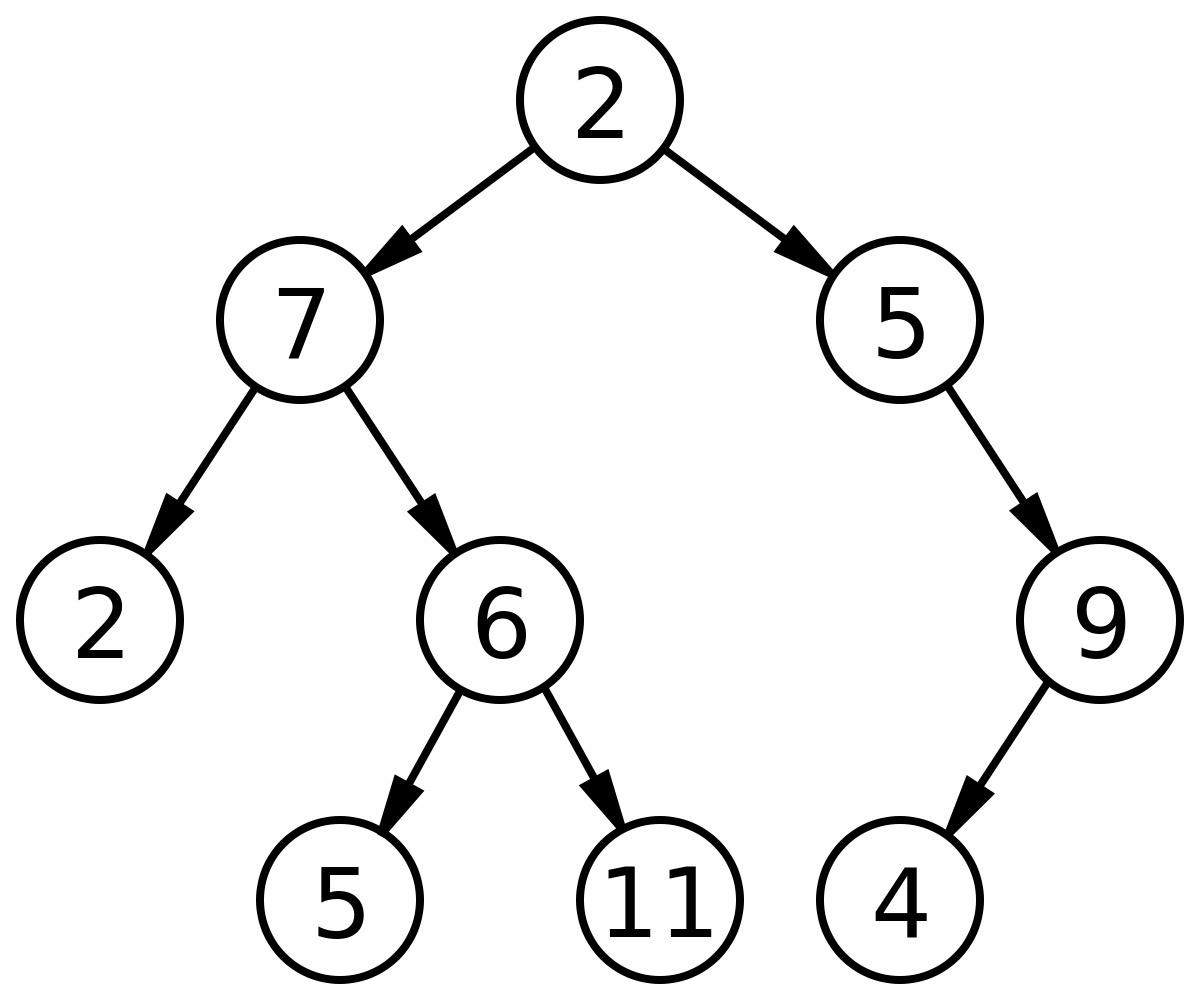
Binary Tree Level Order Traversal
- Leetcode: https://leetcode.com/problems/binary-tree-level-order-traversal/
- Given a binary tree, return the level order traversal of its nodes' values. (ie, from left to right, level by level).
BFS Solution
class Solution:
def levelOrder(self, root: TreeNode) -> List[List[int]]:
if root == None:
return []
ret = [[]]
queue = []
queue.append(root)
queue.append(None)
level = 0
while len(queue) > 1:
node = queue[0]
queue.pop(0)
if node == None:
ret.append([])
level+=1
queue.append(None)
else:
ret[level].append(node.val)
if node.left:
queue.append(node.left)
if node.right:
queue.append(node.right)
return retTechnical Interviews
By theasocialmatzah
Technical Interviews
- 462



