Formalizing Concurrent Systems: The \(\pi\)-calculus

... in Haskell!

Thomas Dietert

Haskell Exchange

October 13th, 2018

whoami

  • Software Engineer @adjoint_io
    • Distributed systems
    • PL design & implementation
  • Programming Language & Type Theory enthusiast
  •  Reader, boulderer, and American IPA drinker...

Overview

  • Intro to \(\pi\)-calculus​

  • Static Analysis

    • Structural Congruence

    • Bisimilarity

  • Static & Dynamic Semantics

  • Implementation in Haskell

Topics not

covered

  • Encoding...

    • data as processes

    • the lambda calculus

  • ​Names, in depth

  • Static Analysis Implementations

  • Concurrent Evaluation

  • Distributed Systems

    • ​cloud haskell

\(\pi\)

calculus:

a particular method or system of calculation or reasoning.

\(\pi\)(process)-calculus 

a model of the changing connectivity of interactive systems

  • models networking in the broad, modern sense
  • can be seen as a basic model of computation
  • rests upon the primitive notion of interaction

an open calculus with respect to names

$$ \begin{aligned} \text{names:} \quad \forall x & \in \mathcal{N} \\ \text{co-names:} \quad \forall \overline{x} & \in \overline{\mathcal{N}} \end{aligned}$$

names can be channels or variables.

Variables are implementation dependent.

But why... ?

Reasoning about distributed systems is hard.

concurrent

  • Did my "bug-fix"...
  • Did my "optimization"...

Are these two programs equivalent?

Static Analyses

... change the semantics of my program?

more formally put,

\(\pi\)-calculus gives us...

Operational Congruences:

  • when do two processes have the same behavior?
  • when does a process meet a specification?
  • when is an abstract machine (evaluator) correct?

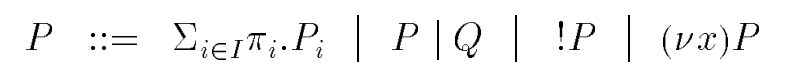
In a summand \(\pi.P\) the prefix \(\pi\) represents an atomic action, the first action performed by  \(\pi.P\). There are two basic forms of \(\pi\) :

Monadic \(\pi\)-calculus

Monadic \(\pi\)-calculus

\(|\; P + Q \)

but summation is often elided to simplify static analysis such as structural congruence, bisimilarity, and evalution.

some syntactic sugar...

$$ x(y).0 \implies x(y) \\ \overline{x}\langle y \rangle .0 \implies \overline{x}\langle y \rangle $$

Null processes are often omitted at the end of process expressions.

Structural Congruence

Processes \( P \) and \( Q \) are structurally congruent, written \( \equiv \),  if we can transform one into the other via a finite sequence steps that preserve the semantics of the process expression.

Structural Congruence

Change of bound names (\(\alpha\)-equivalence)

\( \begin{aligned} P \mid 0 & \equiv P \\ P \mid Q & \equiv Q \mid P \\ P \mid ( Q \mid R )  & \equiv (P \mid Q) \mid R  \end{aligned}\)

\( \begin{aligned} & (\nu x) (P \mid Q) \equiv P \mid (\nu x)Q \quad\quad\quad\quad if x \not\in \text{fn}(P) \\ & (\nu x) 0 \equiv 0, \ (\nu x)(\nu y) P \equiv (\nu y)(\nu x) P \end{aligned} \)

\( !P \equiv P \mid !P \)

(1)

(2)

(3)

(4)

Prove that \((\nu a)(Q \mid P) \equiv P \mid Q \)

if \(a \not\in \ \text{fn}(P) \cup \text{fn}(Q) \)

$$ \equiv (Q \mid P) \mid (\nu a)\, 0 $$

$$ \equiv (Q \mid P) \mid 0 $$

$$ \equiv Q \mid P $$

$$ \equiv P \mid Q $$

$$ (2) $$

$$ (3) $$

$$ (3) $$

$$ (2) $$

$$ (2) $$

\( \begin{aligned} P \mid 0 & \equiv P \\ P \mid Q & \equiv Q \mid P \\ P \mid ( Q \mid R )  & \equiv (P \mid Q) \mid R  \end{aligned}\)

 

\( \begin{aligned} & (\nu x) (P \mid Q) \equiv P \mid (\nu x)\,Q \quad if x \not\in \text{fn}(P) \\ & (\nu x) \,0 \equiv 0, \ (\nu x)(\nu y) P \equiv (\nu y)(\nu x) P \end{aligned} \)

$$(2)$$

$$(3)$$

P \mid Q \equiv (\nu a)(Q \mid P)
\equiv (\nu a)((Q \mid P) \mid 0)

$$ \begin{aligned} \text{fn}(0) \ & = \  \emptyset \\ \text{fn}(\overline{x}\langle y \rangle .P) \ & = \ \{x,y\} \cup \text{fn}(P) \\ \text{fn}((\nu x)P) \ & = \ \text{fn}(P) \setminus \{x\} \end{aligned}  $$

$$ \begin{aligned} \text{fn}(P \mid Q) \ & = \ \text{fn}(P) \cup \text{fn}(Q) \\ \text{fn}(x(y).P) \ & = \ (\text{fn}(P) \setminus \{y\}) \cup \{x\} \\ \text{fn}(!P) \ & = \ \text{fn}(P) \end{aligned} $$

$$\begin{aligned} * \quad \text{bn}(\overline{x}\langle y \rangle) \ & = \ \emptyset \\ \text{bn}(x(y)) \ & = \ \{y\}  \end{aligned}$$ 

$$ (*)$$

$$ (*)$$

Free/Bound Names

Reduction Rules

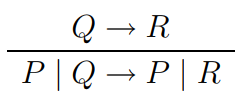
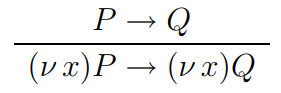
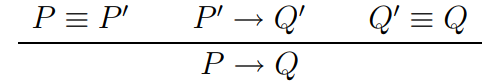
$$\text{PAR}:$$

$$\text{RES}:$$

$$\text{COMM}:$$

$$\text{STRUCT}:$$

$$\prime$$

$$ P $$

$$ P^{\prime} $$

$$ Q $$

\overline{x}\langle \widetilde{z} \rangle.P \mid x(\widetilde{y}).Q \rightarrow P \mid \{\widetilde{y} / \widetilde{z}\} Q

Example Reduction

$$ $$

\equiv \quad \ \, !w(x).\overline{x} \langle z \rangle \mid (\nu x)(x(y) \mid \overline{w} \langle x \rangle)
(\nu x) (x(y) \mid \overline{w} \langle x \rangle ) \mid \; !w(x).\overline{x}\langle z \rangle
\equiv \quad \, (w(x).\overline{x} \langle z \rangle \mid \; !w(x).\overline{x} \langle z \rangle) \mid (\nu x)(x(y) \mid \overline{w} \langle x \rangle)
\equiv \quad \, (\nu x') (w(x).\overline{x} \langle z \rangle \mid \; !w(x).\overline{x} \langle z \rangle \mid x'(y) \mid \overline{w} \langle x' \rangle)
\equiv \quad \, (\nu x') (w(x).\overline{x} \langle z \rangle \mid \overline{w} \langle x' \rangle \mid x'(y) \mid \; !w(x).\overline{x} \langle z \rangle)
\rightarrow \quad (\nu x') (\overline{x'} \langle z \rangle \mid x'(y) \mid \; !w(x).\overline{x} \langle z \rangle)
\rightarrow \quad (\nu x') (!w(x).\overline{x} \langle z \rangle)
\equiv \quad \, (\nu x') (x'(y) \mid \overline{x'} \langle z \rangle \mid \; !w(x).\overline{x} \langle z \rangle)

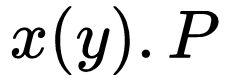
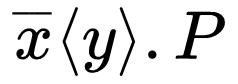
\(x(\widetilde{y}).P\)

\(\overline{x}\langle\widetilde{y}\rangle.P\)

$$\implies$$

$$\implies$$

Polyadic \(\pi\)-calculus

more syntactic sugar...

$$ \begin{aligned} x(y,z).P \; \equiv & \;\;x(y).x(z).P \\ \overline{x}\langle y,z \rangle \; \equiv & \; \; \overline{x}\langle y \rangle . \overline{x} \langle z \rangle . P \end{aligned} $$

... maybe ?

$$ $$

$$ \equiv $$

x(y).x(z) \mid \overline{x}\langle y_{1} \rangle . \overline{x}\langle z_{1} \rangle \mid \overline{x}\langle y_{2} \rangle . \overline{x}\langle z_{2} \rangle
x(z) \mid \overline{x}\langle z_{1} \rangle \mid \overline{x}\langle y_{2} \rangle . \overline{x}\langle z_{2} \rangle
x(z) \mid \overline{x}\langle y_{1} \rangle . \overline{x}\langle z_{1} \rangle \mid \overline{x}\langle z_{2} \rangle
x(y,z)\;\mid\;\overline{x}\langle y_{1},z_{1} \rangle \; \mid \; \overline{x} \langle y_{2},z_{2} \rangle
\rightarrow

The correct conversion

$$ $$

\begin{aligned} x(y_{1}, \cdots , y_{n}) \; &\implies \; x(w).w(y_{1}). \cdots . w(y_{n}) \\ \overline{x}\langle y_{1}, \cdots, y_{n} \rangle \; &\implies \; (\nu w)\overline{x}\langle w \rangle . \overline{w} \langle y_{1} \rangle . \cdots . \overline{w}\langle y_{n} \rangle \end{aligned}

Polyadic \(\pi\)-calculus

$$ \mid \; x(\widetilde{y}).P  $$

Receive on channel \(x\), bind the results to \(\widetilde{y}\), then run \(P\)

Send the values  \(\widetilde{y}\) over channel \(x\), then run \(P\)

$$ \mid \; \overline{x}\langle \widetilde{y} \rangle .P $$

Reduction Rules pt. 2

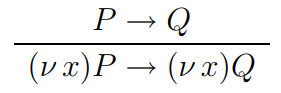
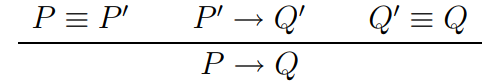
$$ x(\widetilde{y}).P \mid \overline{x}\langle \widetilde{z} \rangle.Q \rightarrow P \mid \{\widetilde{y} / \widetilde{z}\}Q$$

$$RES:$$

$$COMM:$$

$$STRUCT:$$

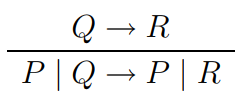
$$\text{PAR}:$$

$$\prime$$

$$ P $$

$$ P^{\prime} $$

$$ Q $$

Bisimilarity

Can process \(P\) simulate process \(Q\), and can process \(Q\) simulate process \(P\)?

A symmetric, binary relation \(\mathcal{S}\) on agents (processes) \(P\) and \(Q\), written \(P\mathcal{S}Q\), satisfying:

P \mathcal{S} Q \wedge P \xrightarrow{\alpha} P' \implies \exists Q' : Q \xrightarrow{\alpha} Q' \wedge P' \mathcal{S} Q'

"if \(P\) can step to \(P\prime\) on some action \(\alpha\), then Q can do the same action, stepping to \(Q\prime\) such that \(P\prime\) and \(Q\prime\) are bisimilar."

$$ \tau.P $$

$$ \tau.P \xrightarrow{\tau} P $$

$$ \tau.P \mid Q \xrightarrow{\tau} P \mid Q $$

Weak Bisimilarity

"Observational Equivalence"

P \mathcal{R} Q \wedge P \xrightarrow{\alpha} P' \implies \exists Q' : Q \xrightarrow{\lambda} Q' \wedge P' \mathcal{R} Q' \\ \text{where} \quad \forall xy. \xrightarrow{\lambda} \; \in \{ \xrightarrow{x(y)}, \xrightarrow{\overline{x}\langle y \rangle}, \xrightarrow{\tau}^{*} \}

Strong Bisimilarity

P \mathcal{R} Q \wedge P \xrightarrow{\alpha} P' \implies \exists Q' : Q \xrightarrow{\lambda} Q' \wedge P' \mathcal{R} Q' \\ \text{where} \quad \forall xy. \xrightarrow{\lambda} \; \in \{ \xrightarrow{x(y)}, \xrightarrow{\overline{x}\langle y \rangle}, \xrightarrow{\tau}^{*} \}

A Simple Type System

$$ $$

$$ \begin{aligned} \delta \; ::= &  \;\text{chan} \, [\delta_{1}, \cdots, \delta_{n}] \\ \mid & \; \; \tau \end{aligned}$$ 

$$ ... ? $$

$$ \Delta \; ::= \; \{ x_{1} : \delta_{1}, \cdots, x_{n} : \delta_{n} \} $$

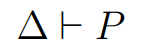
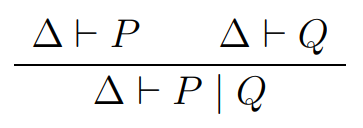
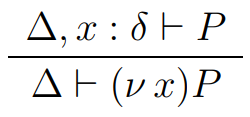
$$ \Delta \vdash P \\ \Delta \vdash \; !P $$

$$ \Delta \vdash 0 $$

$$ \Delta(x) = \text{chan} \,[\delta_{1}, \ldots \delta_{n}] \quad \; \Delta, y_{1} : \delta_{1}, \ldots, y_{n} : \delta_{n} \vdash P \\ \Delta \vdash x(y_{1}, \ldots, y_{n}).P $$

$$ \Delta(x) = \text{chan} \, [\Delta(y_{1}), \ldots, \Delta(y_{n})] \quad \; \Delta \vdash P \\ \Delta \vdash \overline{x}\langle y_{1}, \ldots, y_{n}\rangle . P$$ 

$$ \text{T-PAR}:$$ 

$$ \text{T-NIL}:$$ 

$$\text{T-REPL}:$$

$$ \text{T-RES}:$$ 

$$ \text{T-INPUT}:$$ 

$$ \text{T-OUTPUT}:$$ 

Polyadic, Asynchronous

\(\pi\)-calculus

It is well known that synchronous communication can be simulated using explicit acknowledgments in an asynchronous calculus

 

\overline{x}\langle \widetilde{y} \rangle . P \Longrightarrow \overline{x}\langle \widetilde{y} \rangle
\text{COMM:} \ \overline{x} \langle \widetilde{y} \rangle . P \mid x(\widetilde{z}) . Q \rightarrow P \mid \{\widetilde{y}/\widetilde{z}\}Q
(\nu k)(\overline{x}\langle \widetilde{y}, k \rangle \mid k().P \mid x(\widetilde{z}, k).(\overline{k}\langle \rangle \mid Q))
\rightarrow \quad (\nu k)(k().P \mid \overline{k}\langle \rangle \mid \{\widetilde{y}/\widetilde{z}\}Q)
\rightarrow \quad (\nu k) ( P \mid \{\widetilde{y}/\widetilde{z}\} Q)

Simulating Synchronicity:

This restriction makes it significantly simpler to implement replication, since it becomes easy to detect when we need to create a new copy of the replicated process.

!x(\widetilde{y}).P \mid \overline{x}\langle \widetilde{z} \rangle . Q \rightarrow \; !x(\widetilde{y}).P \mid \{\widetilde{y}/\widetilde{z}\} P \mid Q
!P \quad \Longrightarrow \quad !x(\widetilde{y}).P
!P \equiv P \mid !P
\begin{aligned} P, Q, R \ \coloneqq{}& \ P \mid Q \\ \mid{}& \ (\nu x)P \\ \mid{}& \ \overline{x}\langle \widetilde{y} \rangle \\ \mid{}& \ x(\widetilde{y}).P \\ \mid{}& \ !x(\widetilde{y}).P \\ \mid{}& \ 0 \end{aligned}

Syntax

Reduction Rules 

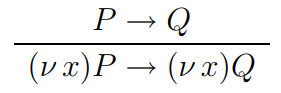
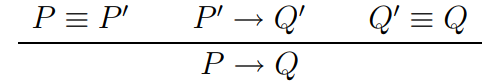
$$RES:$$

$$COMM:$$

$$STRUCT:$$

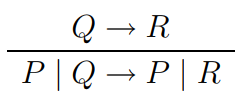
$$\text{PAR}:$$

$$\prime$$

$$ P $$

$$ P^{\prime} $$

$$ Q $$

$$ .P $$

$$ P \mid $$

\overline{x}\langle \widetilde{z} \rangle \mid \; !x(\widetilde{y}).P \rightarrow \{\widetilde{y}/\widetilde{z}\}P \mid \; !x(\widetilde{y}).P
\overline{x}\langle \widetilde{z} \rangle.P \mid x(\widetilde{y}).Q \rightarrow P \mid \{\widetilde{y} / \widetilde{z}\} Q

$$\text{COMM-REPL-INP}:$$

Typing Rules

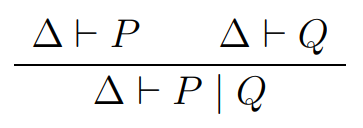
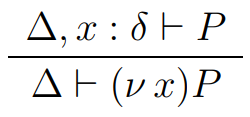
$$ \Delta \vdash P \\ \Delta \vdash \; !P $$

$$ \Delta \vdash 0 $$

$$ \Delta(x) = \text{chan} \,[\delta_{1}, \ldots \delta_{n}] \quad \; \Delta, y_{1} : \delta_{1}, \ldots, y_{n} : \delta_{n} \vdash P \\ \Delta \vdash \, x(y_{1}, \ldots, y_{n}).P $$

$$ \Delta(x) = \text{chan} \, [\Delta(y_{1}), \ldots, \Delta(y_{n})] \quad \; \Delta \vdash P \\ \Delta \vdash \overline{x}\langle y_{1}, \ldots, y_{n}\rangle$$ 

$$ \text{T-PAR}:$$ 

$$ \text{T-NIL}:$$ 

$$\text{T-REPL}:$$

$$ \text{T-RES}:$$ 

$$ \text{T-INPUT}:$$ 

$$ \text{T-OUTPUT}:$$ 

$$ .P $$

$$ \Delta \vdash P $$

$$ ! $$

\text{-REPL-}

Implementation


type PName = Name Proc
type Bindings p = Bind [PName] p

data Proc
  = PNil                                -- ^ 0
  | PName PName                         -- ^ x,y, or z
  | PPar Proc Proc                      -- ^ P | Q
  | POutput Proc [Proc]                 -- ^ x<y1..yN>
  | PInput Proc (Bindings Proc)         -- ^ x(z1..zN)
  | PReplInput Proc (Bindings Proc)     -- ^ !x(z1..zN)
  | PRestrict (Bind (PName,TProc) Proc) -- ^ new x:t in P
  deriving (Show, Generic)

Syntax

CAS (Capture Avoiding Substitution)

package:  unbound-generics

{-# LANGUAGE MultiParamTypeClasses #-}
{-# LANGUAGE FlexibleInstances #-}
{-# LANGUAGE UndecidableInstances #-}
{-# LANGUAGE DeriveGeneric #-}

...

import Unbound.Generics.LocallyNameless

...

instance Alpha Proc

instance Subst Proc Proc where
  isvar p =
    case p of
      PName nm -> Just (SubstName nm)
      _ -> Nothing

Types


data TProc    
  = TChan [TProc]    
  | TProc
  deriving (Show, Generic)

instance Alpha TProc
instance Subst Proc TProc

$$ \tau $$

a small DSL

... almost

nil :: Proc
nil = PNil

var :: [Char] -> Proc
var x = PName (s2n x)

par :: Proc -> Proc -> Proc
par p q = PPar p q

output :: [Char] -> [[Char]] -> Proc
output x ys = POutput (var x) (map var ys)

input :: [Char] -> [[Char]] -> Proc -> Proc
input x ys p = PInput (var x) (bind (map s2n ys) p)

replinput :: [Char] -> [[Char]] -> Proc -> Proc
replinput x ys p = PReplInput (var x) (bind (map s2n ys) p)

res :: [Char] -> TProc -> Proc -> Proc
res x t p = PRestrict (bind (s2n x, t) p)

chan :: [TProc] -> TProc
chan = TChan

Typechecking


type TypeEnv = Map PName TProc

data TypeError
  = TypeError Proc TProc TProc
  | InvalidChanType Proc TProc
  | UnboundVariable (Name Proc)
  deriving (Show)

type TypecheckM = FreshMT (ExceptT TypeError (Reader TypeEnv))

runTypecheckM :: TypecheckM a -> Either TypeError a
runTypecheckM = flip runReader mempty . runExceptT . runFreshMT

lookupTypeEnv 
  :: PName 
  -- ^ Name of variable to look up
  -> TypecheckM (Maybe TProc)
lookupTypeEnv pnm = do
  env <- ask
  pure (Map.lookup pnm env)

extendTypeEnv 
  :: NonEmpty (PName,TProc)
  -- ^ List of variable names and types to add to the type environment
  -> TypecheckM a 
  -- ^ Computation over which to extend the type environment
  -> TypecheckM a
extendTypeEnv xts = 
  local (Map.union $ Map.fromList xts)

a few helpers...

typecheck 
  :: Proc 
  -> TypecheckM TProc
typecheck p = 
  case p of
    ...

$$ \Delta \vdash 0 $$

$$ \text{T-NIL}:$$ 

typecheck 
  :: Proc 
  -> TypecheckM TProc
typecheck p =
  case p of

    PNil -> pure TProc

    ...
typecheck 
  :: Proc 
  -> TypecheckM TProc
typecheck p =
  case p of

    ...

    PName x -> do
      mType <- lookupTypeEnv x
      case mType of
        Nothing -> throwError (UnboundVariable x)
        Just t -> pure t

    ...

those names tho...

typecheck 
  :: Proc 
  -> TypecheckM TProc
typecheck p =
  case p of

    ...

    PPar p q -> do
      typecheck p
      typecheck q
      pure TProc

    ...

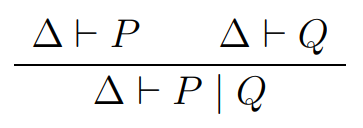
$$ \text{T-PAR}:$$ 

typecheck 
  :: Proc 
  -> TypecheckM TProc
typecheck p =
  case p of

    ...

    POutput x ys -> do
      xType <- typecheck x
      ysTypes <- mapM typecheck ys
      let xExpectedType = TChan ysTypes
      if xType == xExpectedType
        then pure TProc
        else throwError (TypeError x xType xExpectedType)
 
    ...

$$ \Delta(x) = \text{chan} \, [\Delta(y_{1}), \ldots, \Delta(y_{n})] \\ \Delta \vdash \overline{x}\langle y_{1}, \ldots, y_{n}\rangle$$ 

$$ \text{T-OUTPUT}:$$ 

typecheck 
  :: Proc 
  -> TypecheckM TProc
typecheck p =
  case p of

    ...

    PInput x bys -> do
      xType <- typecheck x
      case xType of
        TProc -> throwError (InvalidChanType x xType)
        TChan ts -> do
          (ys, p) <- unbind bys
          extendTypeEnv (zip ys ts) (typecheck p)

    ...

$$ \Delta(x) = \text{chan} \,[\delta_{1}, \ldots \delta_{n}] \quad \; \Delta, y_{1} : \delta_{1}, \ldots, y_{n} : \delta_{n} \vdash P \\ \Delta \vdash x(y_{1}, \ldots, y_{n}).P $$

$$ \text{T-INPUT}:$$ 

typecheck 
  :: Proc 
  -> TypecheckM TProc
typecheck p =
  case p of

    ...

    PReplInput x bys -> do
      xType <- typecheck x
      case xType of
        TProc -> throwError (InvalidChanType x xType)
        TChan ts -> do
          (ys, p) <- unbind bys
          extendTypeEnv (zip ys ts) (typecheck p)

    ...

$$ \Delta(x) = \text{chan} \,[\delta_{1}, \ldots \delta_{n}] \quad \; \Delta, y_{1} : \delta_{1}, \ldots, y_{n} : \delta_{n} \vdash P \\ \Delta \vdash \; !x(y_{1}, \ldots, y_{n}).P $$

$$ \text{T-REPL-INP}:$$ 

typecheck 
  :: Proc 
  -> TypecheckM TProc
typecheck p =
  case p of

    ...

    PRestrict bxp -> do
      ((x,t),p) <- unbind bxp
      case t of
        TProc -> throwError (InvalidChanType (PName x) t)
        TChan _ -> extendTypeEnv [(x,t)] (typecheck p)

$$ \text{T-RES}:$$ 

$$ $$

$$ \Delta, x : \delta \vdash P \\ \Delta \vdash (\nu \, x : \delta) P$$

type inference left as an exercise for the reader...

Evaluation
 

An Abstract Machine

...

It is much more important for a \(\pi\)-calculus abstract machine to provide fair execution, guaranteeing that runnable processes will eventually be executed, and that processes waiting to communicate on a channel will eventually succeed (if sufficient communication partners become available).

- The Polyadic \(\pi\)-calculus, p. 99-100


data ChanQueueElem
  = Reader (Bindings Proc)
  | Writer [Proc]
  | ReplReader (Bindings Proc)

type ChanQueue = Seq ChanQueueElem
type Heap = Map PName ChanQueue
type RunQueue = Seq Proc

data MachineState = MachineState
  { evalHeap :: Heap
  , evalRunQueue :: RunQueue
  }

data ReductionRule
  = RuleNil
  | RulePrl
  | RuleRes
  | RuleInpW
  | RuleInpR
  | RuleOutW
  | RuleOutR
  | RuleOutRStar
  | RuleReplW
  | RuleReplR
  deriving (Show)

data ReductionStep =
  ReductionStep ReductionRule MachineState
  deriving (Show)

Reduction Rules

type EvalM a =
  FreshMT
    (StateT MachineState
      (WriterT [ReductionStep]
        (Except EvalError
        )
      )
    ) a
pushRunQueue :: Proc -> EvalM ()
enqueueRunQueue :: Proc -> EvalM ()
dequeueRunQueue :: EvalM (Maybe Proc)

insertHeap :: PName -> ChanQueue -> EvalM ()
lookupHeap :: PName -> EvalM ChanQueue

peekChanQueue :: PName -> EvalM ChanQueueElem
dequeueChanQueue :: PName -> EvalM ChanQueueElem
enqueueChanQueue :: PName -> ChanQueueElem -> EvalM ()

Evaluation Monad

 

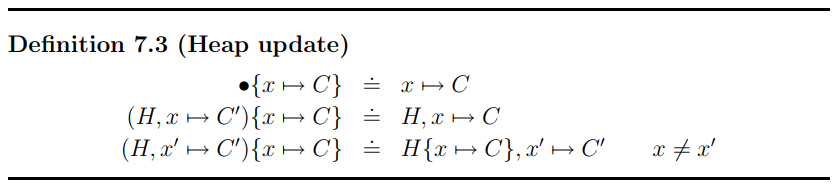
insertHeap :: PName -> ChanQueue -> EvalM ()
insertHeap pnm cq =
  modify $ \evalState ->
    evalState { evalHeap = Map.insert pnm cq (evalHeap evalState) }
runEvalM :: MachineState -> EvalM () -> Either EvalError [ReductionStep]
runEvalM machineState =
  fmap snd . runExcept . runWriterT . flip evalStateT machineState . runFreshMT
runMachine :: Proc -> Either EvalError [ReductionStep]
runMachine initProc =
    runEvalM (initMachineState initProc) machineLoop
  where
    machineLoop = do
      mProc <- dequeueRunQueue
      case mProc of
        -- If no processes in run queue, terminate.
        Nothing -> pure ()
        -- Otherwise, evaluate the process at the head of the run queue
        Just p -> eval p >> machineLoop
-- | Evaluate a process at the head of the run queue, 
-- returning the reduction rule used to evaluate the 
-- given process expression.
eval :: Proc -> EvalM ()
eval proc = do
  rule <-
    case proc of
      
      {- Reduction step here... -}

  -- Emit the reduction rule and resulting machine state
  machineState <- get
  tell [ReductionStep rule machineState]
eval :: Proc -> EvalM ()
eval proc = do
  rule <-
    case proc of
      PNil -> pure RuleNil

      ...

  ...

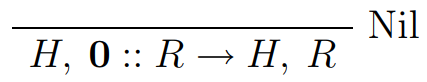
those names tho...

eval :: Proc -> EvalM ()
eval proc = do
  rule <-
    case proc of
  
      ...

      PName pnm -> panic "Trying to eval a name..."
 
      ...

  ...
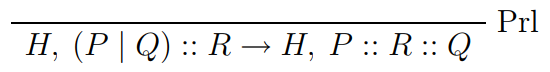
eval :: Proc -> EvalM ()
eval proc = do
  rule <-
    case proc of
 
      ... 

      PPar p q -> do
        pushRunQueue p
        enqueueRunQueue q
        pure RulePrl

      ...    

  ...
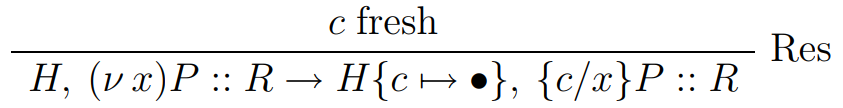
eval :: Proc -> EvalM ()
eval proc = do
  rule <-
    case proc of

      ...

      PRestrict bxp -> do
        ((x,_),p) <- unbind bxp
        insertHeap x Empty
        pushRunQueue p
        pure RuleRes
 
      ...

  ...
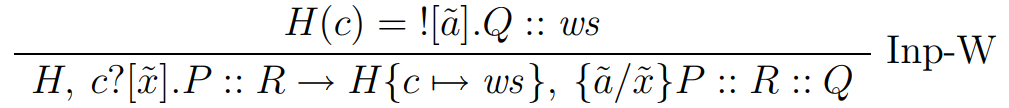
eval :: Proc -> EvalM ()
eval proc = do
  rule <-
    case proc of

      ...

      PInput (PName c) bxs -> do
        cq <- lookupHeap c
        case cq of
          Writer pas :<| ws -> do
            (xs, p) <- unbind bxs
            let as = map pName pas
                pxs = map PName xs
                p' = substs (zip as pxs) p
            insertHeap c ws
            pushRunQueue p'
            pure RuleInpW

            ...
 
       ...

  ...
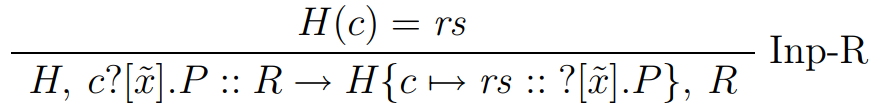
eval :: Proc -> EvalM ()
eval proc = do
  rule <-
    case proc of

      ...

      PInput (PName c) bxs -> do
        cq <- lookupHeap c
        case cq of

          ...

          rs -> do
            insertHeap c (rs |> Reader bxs)
            pure RuleInpR

      ...

  ...
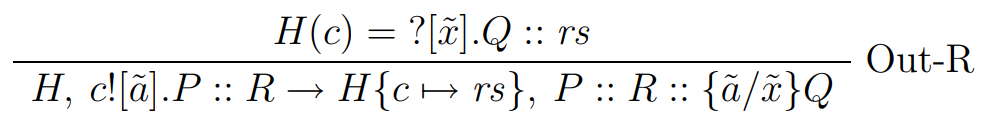
eval :: Proc -> EvalM ()
eval proc = do
  rule <-
    case proc of

      ...
    
      POutput (PName c) pas -> do
        cq <- lookupHeap c
        case cq of
          Reader bxs :<| rs -> do
            (xs, q) <- unbind bxs
            insertHeap c rs
            let as = map pName pas
                pxs = map PName xs
                q' = substs (zip as pxs) q
            enqueueRunQueue q'
            pure RuleOutR
           
          ...
       
      ...

  ...
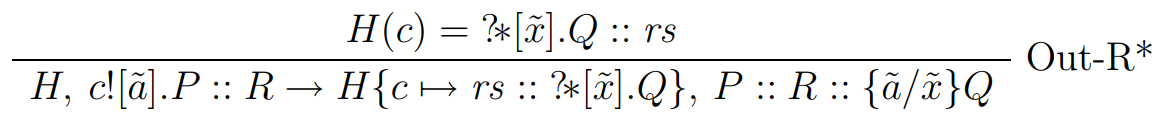
eval :: Proc -> EvalM ()
eval proc = do
  rule <-
    case proc of

      ...

      POutput (PName c) pas -> do
        cq <- lookupHeap c
        case cq of
          
          ...

          rr@(ReplReader bxs) :<| rs -> do
            (xs, q) <- unbind bxs
            insertHeap c (rs |> rr)
            let as = map pName pas
                pxs = map PName xs
                q' = substs (zip as pxs) q
            enqueueRunQueue q'
            pure RuleOutRStar

          ...

       ...

   ...
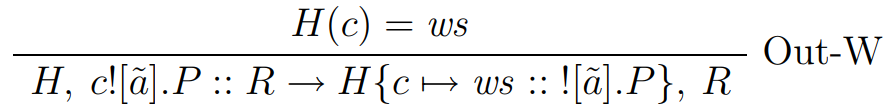
eval :: Proc -> EvalM ()
eval proc = do
  rule <-
    case proc of

      ...

      POutput (PName c) pas -> do
        cq <- lookupHeap c
        case cq of
          
          ...

          ws -> do
            insertHeap c (ws |> Writer pas)
            pure RuleOutW

       ...

   ...
eval :: Proc -> EvalM ()
eval proc = do
  rule <-
    case proc of

      ...      

      PReplInput (PName c) bxs -> do
        cq <- lookupHeap c
        case cq of

          Writer pas :<| ws -> do
            (xs, p) <- unbind bxs
            insertHeap c ws
            pushRunQueue proc
            let as = map pName pas
                pxs = map PName xs
                p' = substs (zip as pxs) p
            enqueueRunQueue p'
            pure RuleReplW
 
          ...

      ...

  ...
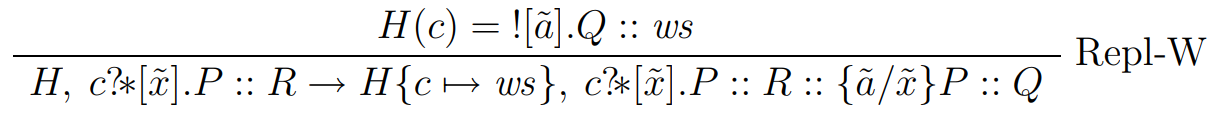
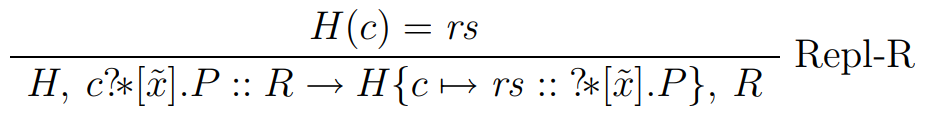
eval :: Proc -> EvalM ()
eval proc = do
  rule <-
    case proc of

      ...      

      PReplInput (PName c) bxs -> do
        cq <- lookupHeap c
        case cq of

          ...

          rs -> do
            insertHeap c (rs |> ReplReader bxs)
            pure RuleReplR

      ...

  ...

Example Reduction

(\nu x)(\overline{x}\langle \rangle \mid \; !x())
\implies
exampleReduction :: Proc
exampleReduction =
  res "x" (chan [])
    (par
      (output "x" [])
      (replinput "x" [] nil)
    )
data ProcError
  = ProcTypeError TypeError
  | ProcEvalError EvalError
  deriving (Show)

process :: Proc -> Either ProcError [ReductionStep]
process p = do
  first ProcTypeError (runTypecheckM (typecheck p))
  first ProcEvalError (runMachine p)
runExampleReduction :: IO ()
runExampleReduction = do
  case process exampleReduction of
    Left err -> panic (show err)
    Right reds -> mapM_ print reds
(\nu x)(\overline{x}\langle \rangle \mid \; !x().P) \\ \text{where} \ P = 0
\begin{aligned} & H, (\nu x)(\overline{x}\langle \rangle \mid \ !x().P) \\ \rightarrow \ & H\{x \mapsto \bullet\}, \ \overline{x}\langle \rangle \mid \ !x().P & \text{Res} \\ \rightarrow \ & H\{x \mapsto \bullet\}, \ \overline{x}\langle \rangle :: \ !x().P & \text{Prl} \\ \rightarrow \ & H\{x \mapsto \langle \rangle\}, \ !x().P & \text{Out-W} \\ \rightarrow \ & H\{x \mapsto \bullet\}, \ !x().P :: P & \text{Repl-W} \\ \rightarrow \ & H\{x \mapsto \; !().P \}, \ P & \text{Repl-R} \end{aligned}

expected reductions:

[2018-10-11 21:33:24] thomas@bonobo:~/github/pi-calculus $ stack ghci src/PolyadicAsync.hs 
Using configuration for pi-calculus:lib to load /home/thomas/github/pi-calculus/src/PolyadicAsync.hs
Configuring GHCi with the following packages: pi-calculus
GHCi, version 8.2.2: http://www.haskell.org/ghc/  :? for help
Loaded GHCi configuration from /home/thomas/.ghci
[1 of 1] Compiling PolyadicAsync    ( /home/thomas/github/pi-calculus/src/PolyadicAsync.hs, interpreted )
Ok, one module loaded.
Loaded GHCi configuration from /tmp/haskell-stack-ghci/820cd9a9/ghci-script
*PolyadicAsync λ> runExampleReduction 
ReductionStep RuleRes 
  (MachineState { 
      evalHeap = fromList [(x,fromList [])]
    , evalRunQueue = fromList [PPar (POutput (PName {pName = x}) []) (PReplInput (PName {pName = x}) (<[]> PNil))]
  })
ReductionStep RulePrl 
  (MachineState {
      evalHeap = fromList [(x,fromList [])]
    , evalRunQueue = fromList [POutput (PName {pName = x}) [], PReplInput (PName {pName = x}) (<[]> PNil)]
  })
ReductionStep RuleOutW 
  (MachineState {
      evalHeap = fromList [(x,fromList [Writer []])]
    , evalRunQueue = fromList [PReplInput (PName {pName = x}) (<[]> PNil)]
  })
ReductionStep RuleReplW 
  (MachineState {
      evalHeap = fromList [(x,fromList [])]
    , evalRunQueue = fromList [PReplInput (PName {pName = x}) (<[]> PNil),PNil]
  })
ReductionStep RuleReplR 
  (MachineState {
      evalHeap = fromList [(x,fromList [ReplReader (<[]> PNil)])]
    , evalRunQueue = fromList [PNil]
  })
ReductionStep RuleNil 
  (MachineState {
      evalHeap = fromList [(x,fromList [ReplReader (<[]> PNil)])]
    , evalRunQueue = fromList []
  })
H, (\nu x)(\overline{x}\langle \rangle \mid \; !x().0)
\rightarrow \ H\{x \mapsto \bullet\}, \ \overline{x}\langle \rangle \mid \ !x().0 \quad \text{Res}
\rightarrow \ H\{x \mapsto \bullet\}, \ \overline{x}\langle \rangle :: \ !x().0 \quad \text{Prl}
\rightarrow \ H\{x \mapsto \langle \rangle\}, \ !x().0 \quad \text{Out-W}
\rightarrow \ H\{x \mapsto \bullet\}, \ !x().0 :: 0 \quad \text{Repl-W}
\rightarrow \ H\{x \mapsto \; !().0 \}, \ 0 \quad \text{Repl-R}
\rightarrow \ H\{x \mapsto \; !().0 \} \quad \text{Nil}

https://github.com/tdietert/pi-calculus

References

communicating  

and mobile  

systems: the

- calculus  

Robin Milner

\(\pi\) 

The Polymorphic Pi-Calculus:
Theory and Implementation

- David N. Turner

Applied \(\pi\ -\) A Brief Tutorial

- Peter Sewell

An Introduction to the \(\pi\)-calculus

- Joachim Parrow

Further Reading

  • Pict: The Programming Language
  • Distributed \(\pi\)-calculus
  • Cryptographic Protocols:
    • Applied \(\pi\)-calculus
    • Spi-calculus
  • Time... and space?

Questions?

\pi

deck

By Thomas Dietert

Made with Slides.com

deck

  • 554

More from Thomas Dietert