Deep Dive into

Big O

What is Big O?

  • Big O is the notation we use to express the runtime or space complexity of an algorithm relative to its input, as the input gets arbitrarily large.
  • Because Big O is about measuring the shape of a growth curve, we express Big O in terms of its largest factor, and drop all others.
  • Calculating Big O is actually a lot of fun, and you're about to learn to love it!

Why You Should Care

  • Being able to evaluate the runtime/space complexity of an algorithm is critical to writing performant code.
    • When asked to optimize an algorithm, one of the first things you might do is determine its Big(O) complexity.

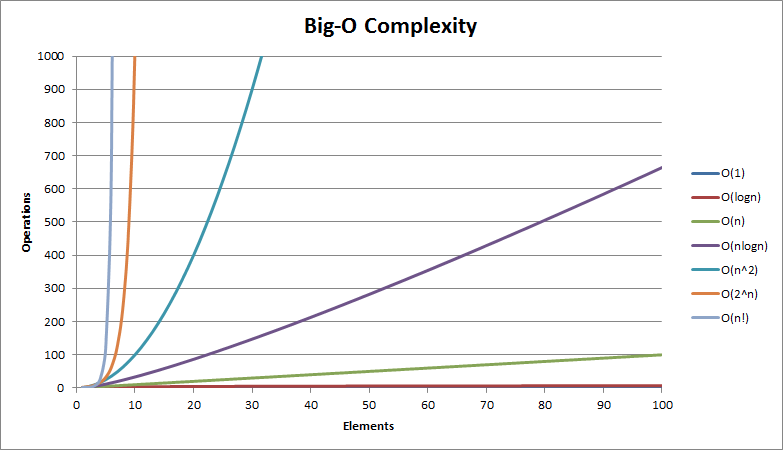
FYI One: This is not all there is to Big-O

FYI Two: Big O, Big Ω, and Big Theta

  • This is a more academic breakdown of what we talk about when we describe Big O. 
    • In academia, Big O actually refers to the upper bound on time (if something is O(n), it's also O(n^2), O(n^3).
    • Big Ω refers to the lower bound on time (if something is O(n), it's also O(log(n)), O(1), etc...
    • Big Theta is actually Big O as we know it - the union between Big O and Big Ω. In the real world, this is what we care about the most!

Basic Strategy

  • Measure the complexity of the algorithm at each and every step.
  • Be concrete: you don't need to use 'n', 'm' etc if you don't want to (at least until the end). Use the name of the inputs of the algorithm, or whatever makes the most sense to you!
  • Add the complexity for each line at the same level of indentation. Multiply inner levels by their outer levels.
  • When you've reduced as far as you can, drop everything but the largest term!
/* Let's start out easy */

function foo(arr) {
	var sum = 0;				
	var product = 1;			

	for (var i = 0; i < arr.length; i++)	
		sum += arr[i];			    
	for (var j = 0; j < arr.length; j++)	
		product *= arr[i];		    

	console.log(sum * product);		
}                  
/* Piece of cake */

function foo(arr) {
	var sum = 0;				// O(1)
	var product = 1;			// O(1)

	for (var i = 0; i < arr.length; i++)	// O(arr)
		sum += arr[i];			    // O(1)
	for (var j = 0; j < arr.length; j++)	// O(arr)
		product *= arr[i];		    // O(1)

	console.log(sum * product);		// O(1)
}                  

// O(1) + O(1) + (O(arr) * O(1)) + (O(arr) * O(1)) + O(1)
// O(3 * arr) => O(arr) => O(n)
/* Another softball */

function bar(arr) {
	for (var i = 0; i < arr.length; i++)		
		for (var j = 0; j < arr.length; j++)		
			console.log(arr[i] + arr[j]);		    
}



/* All good! */

function bar(arr) {
	for (var i = 0; i < arr.length; i++)		// O(arr)
		for (var j = 0; j < arr.length; j++)		// O(arr)
			console.log(arr[i] + arr[j]);		    // O(1)
}

// O(arr) * O(arr) * O(1) => O(arr^2) => O(n^2)

/* Don't worry, you got this */

function baz(arrA, arrB) {
	for (var i = 0; i < arrA.length; i++)	        
		for (var j = 0; j < arrB.length; j++)	    
			console.log(arrA[i] + arrB[j]);		
}

/* See that wasn't so bad */

function baz(arrA, arrB) {
	for (var i = 0; i < arrA.length; i++)	        // O(arrA)
		for (var j = 0; j < arrB.length; j++)	    // O(arrB)
			console.log(arrA[i] + arrB[j]);		// O(1)
}

// O(arrA) * O(arrB) * O(1) => O(nm)
/* Wait, is this a trick? */

function foobar(arr) {
	for (var i = 0; i < arr.length; i++)		
		for (var j = i + 1; j < arr.length; j++)
			console.log(arr[i] + arr[j]);		
}
/* Okay, not so bad... */

function foobar(arr) {
	for (var i = 0; i < arr.length; i++)		// O(arr)
		for (var j = i + 1; j < arr.length; j++)    // on average, between 1 and arr
			console.log(arr[i] + arr[j]);		// O(1)
}

// O(arr) * O(arr-ish) * O(1) => O(n^2)

/* As the size of arr gets large, 
it stops mattering that O(arr-ish) is actually less than O(arr).
The shape of the growth curve will still be similar.
*/

Beyond the basics

  • Recursion
  • Space Complexity
  • Algorithms on algorithms

How to deal with recursion

  • When there is only one recursive branch, this is not much different than a standard "for" loop.
  • When there are multiple recursive branches, the runtime will often be similar to O(branches^depth) - though this is not always the case.
  • When in doubt, write it out.

Branches^depth

  • Depth is relative to the input size
  • For example, a binary search tree with seven nodes is three levels deep. If n = 7, the depth is roughly log(n) (log base 2)
/*
        7
       / \
    4       9
   / \     / \
  1   6   8   12


Seven elements altogether
Three levels deep

*/
/* Let's take it to the limit! */

function fib (n) {
    if (n === 1 || n === 0) return n;
    else return fib(n - 1) + fib(n - 2);
}
/* This is why fib is so slow! */

/*
                     fib(4)
                    /      \
            fib(3)            fib(2)
           /      \          /      \
      fib(2)     fib(1)   fib(1)    fib(0)
      /    \
 fib(1)     fib(0)


our input is equal to 4: n = 4
we go four levels deep, so depth = n
we branch twice with each recursive call

therefore, runtime is O(2^n)!

*/
/* What if we throw some dynamic programming in there? */

function fib (n, memo) {
    if (!memo) var memo = {};

    if (n === 1 || n === 0) return n;
    else if (memo[n]) return memo[n];
    else memo[n] = fib(n - 1, memo) + fib(n - 2, memo);
    return memo[n];
}


/* Such quicker, much dynamic, wow! */

/*
                     fib(4)
                    /      \
            fib(3)            fib(2)
           /      \          /      \
      fib(2)     fib(1)   fib(1)    fib(0)
      /    \
 fib(1)     fib(0)



1. fib(4) = fib(3) + fib(2)
           /
2. fib(3) = fib(2) + fib(1)
             /
3. fib(2) = fib(1) + fib(0) = memo[2]

4. fib(3) = memo[2] + fib(1) = memo[3]

5. fib(4) = memo[3] + fib(2) = memo[3] + memo[2]


*/

/* 

That entire second branch got taken out of the picture
Every step ends up being in constant time, which we only do a maximum of n times
Using a memo cuts runtime down to O(n)!

*/

Space Complexity

  • Big O can also express space complexity
  • Very similar to run time, except instead of counting how many times we need to do work relative to the input size, we calculate how much storage space we use (ex. by storing values in variables, arrays, hashes, etc) relative to the input size (not including the input itself)
  • When we add to the call stack, that takes up space as well
  • An important distinction to remember when calculating space complexity v. time complexity: you can add space, but you can also free up space. You can't take away time.
/* Basic example of calculating space complexity */

function (arr) {
    var arrOfarrs = [];
    for (var i = 0; i < arr.length; i++)
        arrOfarrs.push(arr);
    return arrOfarrs;
}

/*

This would be space O(n^2). Not sure why you would do this, though...

*/
/* Memoized fibonacci revisited */

function fib (n, memo) {
    if (!memo) var memo = {};

    if (n === 1 || n === 0) return n;
    else if (memo[n]) return memo[n];
    else memo[n] = fib(n - 1, memo) + fib(n - 2, memo);
    return memo[n];
}

/* 

This is a lot quicker than the non-memoized version, but remember that it's still recursive, 
so we will eventually have n calls on the call stack. We also have the memo, 
but it ends up not mattering much. It will always contain a little less than n items.

Therefore, space complexity is O(n + n-ish) => O(n)
...which is the same as the non-memoized version!

*/

Multi-Level Algorithms

  • What if you have an algorithm that uses another algorithm? For example, what if you loop over an array of strings and sort each string?
  • Be careful not to confuse the runtime of the outer algorithm with the runtime of inner algorithms
/* Sorting an array of strings */

function sortedStrings (arr) {
    for (var i = 0; i < arr.length; i++)
        arr[i].sort();                        // Let's say that .sort is O(n log n)
}

// Fun fact: different browsers have different implementations for Array.prototype.sort!
/* Sorting an array of strings */


/* The key to understanding this is that we have two algorithms with two different inputs
    sortedStrings takes an array with an array input, with a length of say 'n'
    Array.prototype.sort takes a string input, with a length of say 's'
*/

function sortedStrings (arr) {
    for (var i = 0; i < arr.length; i++)      // O(n)
        arr[i].sort();                            // O(s log s)
}

// O(n) * O(s log s) => O(n * s log s)

Resources and Questions

Big O

By Tom Kelly

Made with Slides.com

Big O

Tech Talk

  • 1,732

More from Tom Kelly