Антон Антонов

Неочевидное – вероятное

\int\limits_{-\infty}^{\infty} x f(x) dx
∫−∞∞xf(x)dx\int\limits_{-\infty}^{\infty} x f(x) dx

Доклады "Курилки" за последние полгода

  1. История                                      13
  2. Биология                                  13
  3. Космос                                         12
  4. Литература, философия               11
  5. Психология                                 10
  6. Физика, химия                          8
  7. Технологии                                  7
  8. Экономика, энергетика                7
  9. Математика                                     0

1

Это физика!

В. Тарасевич

"Поединок"

1963, МГУ

д.ф.-м.н. В. В. Балашов

Высокий уровень абстракции

\lim\limits_{x \to c} f(x) = L \Leftrightarrow
limx→cf(x)=L⇔\lim\limits_{x \to c} f(x) = L \Leftrightarrow
(\forall \varepsilon > 0)(\exists \ \delta > 0) (\forall x \in D)
(∀ε>0)(∃ δ>0)(∀x∈D)(\forall \varepsilon > 0)(\exists \ \delta > 0) (\forall x \in D)
0 < |x - c | < \delta \ \Rightarrow \ |f(x) - L| < \varepsilon
0<∣x−c∣<δ ⇒ ∣f(x)−L∣<ε0 < |x - c | < \delta \ \Rightarrow \ |f(x) - L| < \varepsilon

А по-человечески?

Примеры будут?

Зачем это нужно?

Случайная величина

система элементарных исходов

\Omega = \{1, 2, 3, 4, 5, 6\}
Ω={1,2,3,4,5,6}\Omega = \{1, 2, 3, 4, 5, 6\}

распределение вероятностей

\sum\limits_{\omega \in \Omega} p(w) = 1
∑ω∈Ωp(w)=1\sum\limits_{\omega \in \Omega} p(w) = 1
\Omega
Ω\Omega
p(1) = \ldots = p(6) = \frac16
p(1)=…=p(6)=16p(1) = \ldots = p(6) = \frac16

3500 д.н.э. (!)

\Omega
Ω\Omega
X
XX
Y
YY
P(X) = P(Y) = \frac12
P(X)=P(Y)=12P(X) = P(Y) = \frac12
P(X \, \text{or} \, Y) = \frac56
P(XorY)=56P(X \, \text{or} \, Y) = \frac56
P(X \, \text{and} \, Y) = \frac16
P(XandY)=16P(X \, \text{and} \, Y) = \frac16
X :
X:X :

"Выпало нечётное количество очков"

Y :
Y:Y :

"Выпало строго больше трёх очков"

P_1 = P_2 = 0.8
P1=P2=0.8P_1 = P_2 = 0.8
0.8 + 0.8 = ... (?!)
0.8+0.8=...(?!)0.8 + 0.8 = ... (?!)

Танк будет уничтожен с вероятностью

0.8
0.80.8
0.8
0.80.8
0.2
0.20.2
0.2
0.20.2
A
AA
B
BB
C
CC
D
DD
A = \{ \qquad \qquad \}
A={}A = \{ \qquad \qquad \}
\Omega
Ω\Omega
B = \{ \qquad \qquad \}
B={}B = \{ \qquad \qquad \}
C = \{ \qquad \qquad \}
C={}C = \{ \qquad \qquad \}
D = \{ \qquad \qquad \}
D={}D = \{ \qquad \qquad \}
P(A) + P(C)
P(A)+P(C)P(A) + P(C)
1 - P(D) = 1 - 0.04 = 0.96
1−P(D)=1−0.04=0.961 - P(D) = 1 - 0.04 = 0.96
= 0.8 + 0.8 - 0.64 = 0.96
=0.8+0.8−0.64=0.96= 0.8 + 0.8 - 0.64 = 0.96
- P(A) =
−P(A)=- P(A) =
+\, P(A) + P(B)
+P(A)+P(B)+\, P(A) + P(B)

334277858179225404612400837541072273043933252046644720358295349210233339729451

653318623500070906096690267158057820537143710472954871543071966369497141477376

P(350 \leqslant \Sigma_{100} \leqslant 500) =
P(350⩽Σ100⩽500)=P(350 \leqslant \Sigma_{100} \leqslant 500) =
= 0.5116613
=0.5116613 = 0.5116613
51.2\%
51.2% 51.2\%
throw_dice <- function(n) {
  sample.int(n = 6, size = n, replace = T)
}

emulate <- function(times) {
  x <- replicate(times, sum(throw_dice(100)))
  length(x[x >= 350 & x <= 500]) / length(x)
}

set.seed(42)
emulate(1e6)
# [1] 0.511896

С точностью до третьего знака

за несколько секунд!

51.2\%
51.2% 51.2\%

S. Ulam

N. Metropolis

Метод Монте-Карло (1949)

J. von Neumann

Не считай на бумаге,

симулируй на компьютере!

P(\Sigma_2 = 8)
P(Σ2=8)P(\Sigma_2 = 8)
= \frac{5}{36}
=536= \frac{5}{36}
\Omega
Ω\Omega
P(\Sigma_2 = 8 | Red = 4)
P(Σ2=8∣Red=4)P(\Sigma_2 = 8 | Red = 4)
= \frac16
=16= \frac16
\Omega
Ω\Omega
P(Red = 4 | \Sigma_2 = 8)
P(Red=4∣Σ2=8)P(Red = 4 | \Sigma_2 = 8)
= \frac15
=15= \frac15
\Omega
Ω\Omega
P(A|B) \neq P(B|A)
P(A∣B)≠P(B∣A)P(A|B) \neq P(B|A)

В общем случае

Новая информация может изменить распределение вероятностей!

W. Casscells, A. Schoenberger, T. B. Grayboys, 1978:

  • Редкая болезнь: один больной на тысячу
  • Точность теста: 99%
    (1% ложноположительных срабатываний,
    ложноотрицательных нет)
  • Тест положителен;
    какова вероятность, что пациент болен?
99\%
99%99\%
75\% \text{-} 99\%
75%-99%75\% \text{-} 99\%
50\% \text{-} 75\%
50%-75%50\% \text{-} 75\%
25\% \text{-} 50\%
25%-50%25\% \text{-} 50\%
0\% \text{-} 25\%
0%-25%0\% \text{-} 25\%
A:
A:A:
B:
B:B:

"Пациент болен"

"Тест положителен"

P(A|B) = \, ?
P(A∣B)=?P(A|B) = \, ?
\overline A:
A‾:\overline A:

"Пациент здоров"

P(\overline B| \overline A) = 0.99
P(B‾∣A‾)=0.99P(\overline B| \overline A) = 0.99
P(B|A) = 1
P(B∣A)=1P(B|A) = 1
\overline B:
B‾:\overline B:

"Тест отрицателен"

Ложноотрицательных нет:

Ложноположительных 1%:

P(B| \overline A) = 0.01
P(B∣A‾)=0.01P(B| \overline A) = 0.01
P(A|B) = \frac{0.001}{0.001 + 0.999*0.01}
P(A∣B)=0.0010.001+0.999∗0.01P(A|B) = \frac{0.001}{0.001 + 0.999*0.01}
\approx 9.1\%
≈9.1%\approx 9.1\%

болен

не болен и

тест ложноположителен

P(A|B) = \, ?
P(A∣B)=?P(A|B) = \, ?
A:
A:A:
B:
B:B:

"Пациент болен"

"Тест положителен"

\overline A:
A‾:\overline A:

"Пациент здоров"

\overline B:
B‾:\overline B:

"Тест отрицателен"

infect_population <- function(n, p = 0.001) {
  people <- rep.int(0, n)
  people[as.logical(rbinom(n, 1, p))] <- 1
  people
}

test_population <- function(people, fp_rate = 0.99) {
  n_healthy <- length(people) - sum(people)
  people[people == 1] <- 2
  people[people == 0] <- rbinom(n_healthy, 1, 1 - fp_rate)
  factor(people, labels = c("Healthy, test negative", 
                            "Healthy, test positive", 
                            "Infected"))
}

set.seed(1984)
people <- infect_population(1e6)
res <- summary(test_population(people))
paste0("P(Infected | test positive) = ", 
       sprintf("%3.1f", res["Infected"] / 
                 (res["Infected"] + res["Healthy, test positive"]) 
                 * 100), "%")

# [1] "P(Infected | test positive) = 9.1%"
9.1\%
9.1%9.1\%

Проведём повторный тест:

\frac{0.001}{0.001 + 0.999*0.01}
0.0010.001+0.999∗0.01\frac{0.001}{0.001 + 0.999*0.01}
\frac{0.001}{0.001 + 0.999*0.01*0.01}
0.0010.001+0.999∗0.01∗0.01\frac{0.001}{0.001 + 0.999*0.01*0.01}
\approx 90.9\%
≈90.9%\approx 90.9\%

болен

не болен и

тест ложноположителен

два раза подряд

test_population2 <- function(people, fp_rate = 0.99) {
  n_healthy <- length(people) - sum(people)
  people[people == 1] <- 3
  people[people == 0] <- rbinom(n_healthy, 2, 1 - fp_rate)
  factor(people, labels = c("Healthy, twice negative", 
                            "Healthy, negative/positive", 
                            "Healthy, twice positive",
                            "Infected"))
}

res2 <- summary(test_population2(people))
paste0("P(Infected | twice positive) = ", 
       sprintf("%3.1f", res2["Infected"] / 
                 (res2["Infected"] + res2["Healthy, twice positive"]) 
                 * 100), "%")

# [1] "P(Infected | twice positive) = 90.8%"
Одинарный тест Двойной тест
Истинное значение 0.091 0.909
Монте-Карло 0.091 0.908
90.8\%
90.8%90.8\%

Бесконечное количество обезьян

и собрание сочинений Шекспира

и торговля на фондовой бирже

  1. Средний темп роста рынка: 12%
  2. 100000 инвесторов по $10000
  3. Торгуем каждую неделю, 20 лет
  4. Цена колеблется в диапазоне -5%...+5%
  5. Контрольное значение: "buy and hold"
  6. Все сделки случайны!

Эксперимент стоимостью

$1,000,000,000

set.seed(1337); investor_count <- 100000; initial_balance <- 10000
delta <- 0.05; years <- 20; weeks <- 52
growth_factor <- 1.0 + (0.12 / weeks)
investors <- rep.int(initial_balance, investor_count)
bh_balance <- initial_balance

for (year in 1:years) {
  for (week in 1:weeks) {
    bh_balance <- bh_balance * growth_factor
    investors <- investors * 
      (1 + delta * runif(investor_count, -1, 1)) * growth_factor
  }
}

n_losers <- length(investors[investors < bh_balance])
n_winners <- length(investors[investors > bh_balance])
n_wolves <- length(investors[investors > 1000000])

writeLines(paste(sep = "\n",
        sprintf("Investors %d, initial balance $%.02f", 
                investor_count, initial_balance),
        sprintf("Buy & hold $%.02f, worst $%.02f, best $%.02f", 
                bh_balance, min(investors), max(investors)),
        sprintf("Millionaires %d, winners %d, losers %d", 
                n_wolves, n_winners, n_losers)))

# Investors 100000, initial balance $10000.00
# Buy & hold $109927.40, worst $1546.53, best $4444214.61
# Millionaires 233, winners 31936, losers 68064
  • Всего инвесторов:                    100000
  • Начальный капитал:           $10,000.00
  • Стратегия "buy and hold":   $109,927.40
  • Худший инвестор:               $1,546.53
  • Лучший инвестор:               $4,444,214.61
  • Неудачливых инвесторов:        68064
  • Удачливых инвесторов:            31936
  • Миллионеров:                            233

Результаты

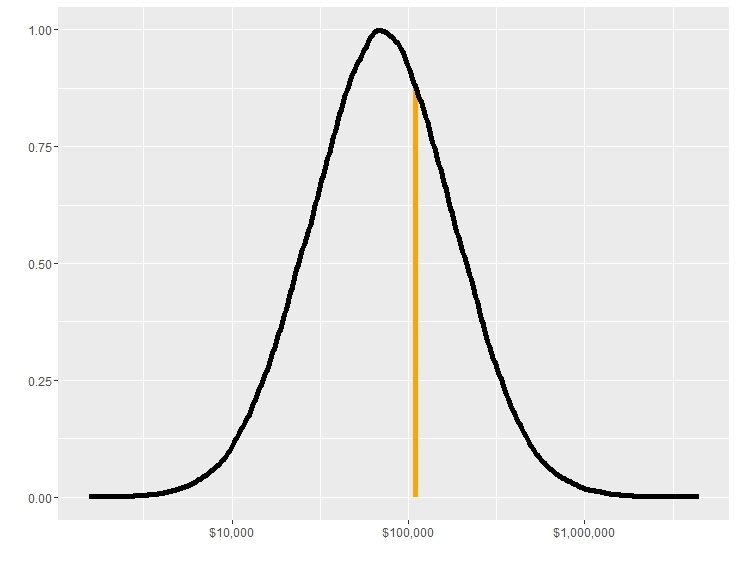
Buy and hold

Начальный капитал

1. Фундаментальные математические исследования крайне важны

2. Вероятности обманчивы,

особенно в контексте медицинских и финансовых рисков

3. Метод Монте-Карло —

верный помощник при оценивании сложных вероятностей

NB!

Kurilka Gutenberga

By Antonov Anton

Made with Slides.com

Kurilka Gutenberga

The talk I gave at Kurilka Gutenberga, a popular science event (St. Petersburg, 30.09.2016).

  • 587

More from Antonov Anton

  • Воспроизводимые исследования в контексте языка R
    Antonov Anton
    440
  • Воспроизводимые исследования в контексте языка R (preview)
    Antonov Anton
    617