How Uses Formal Methods
Amazon
Web
Services
Paper
Authors:
Chris Newcombe, Tim Rath, Fan Zhang, Bogdan Munteanu, Marc Brooker, Michael Deardeuff
Released:
29th September, 2014
Company:
Amazon

Amazon Web Services (AWS), is a collection of cloud computing services, also called web services, that make up a cloud-computing platform offered by Amazon.com.
CUSTOMERS






PRODUCTS
S3
DynamoDB


EBS
Many Others...
Elastic Beanstalk, Auto Scaling, Virtual Private Cloud, Elastic Load Ballancing...
DISTRIBUTED ALGORITHM
Distributed algorithms are algorithms designed to run on multiple processors, without tight centralized control.
FORMAL METHODS
A particular kind of mathematically based techniques for the specification, development and verification of software and hardware systems.
ALLOY
Developed in MIT
Taught in University Of Iceland
TLA+
Temporal Logic of Actions
Released in 1999 by Leslie Lamport
PlusCalc, C-like syntax
TLC model checker
N Queens Problem

Fit N Queens on NxN spaces
Solvable for all
8 Queens on chess-board
SETJA LIGHT THEME!

AWS had a problem.
Human intuition is poor at estimating the true probability of supposedly "extremely rare" combinations of events in systems operating at a scale of millions of requests per second
The number of reachable states in the code is astronomical
FIRST EVIDENCE
C.N. found that Pamela Zave used Alloy to find serious bugs in the membership protocol of a distributed system called Chord.
Alloy not expressive enough for AWS. No practical way to represent rich data structures
That formal methods could be the solution
A New Hope
C.N. found a TLA+ specification for a algorithm in AWS's problem domain: the Paxos consensus algorithm
Gave confidence that TLA+ worked for real-world systems

Further confidence in TLA+
We became more confident when we learned that a team of engineers at DEC/Compaq had used TLA+ to specify and verify some intricate cache-coherency protocols for the Alpha series of multi-core CPUs. We read one of the specifications and found that these were sophisticated distributed algorithms, involving rich message passing, fine-grain concurrency, and complex correctness properties
The Wildfire Challenge Problem
Auxiliary paper
Leslie Lamport, Madhu Sharma, Mark Tuttle, and Yuan Yu
Compaq
4 Jan 2001
Wildfire was the code name for a family of multiprocessor computers made by Compaq containing up to 32 processors.
Auxiliary paper
It has the most complicated cache-coherence protocol we know of
into which they deliberately inserted a bug!
🕷
Georges Gonthier solved the problem along with finding another error
I did spot a bug, but was a bit disappointed because it seemed too trivial, so I carried on, as I was interested in understanding how the whole thing ticked. . . It just dawned on me last night that there was indeed a more subtle problem with the spec.
Auxiliary paper
THE BOTTOM LINE
From the fall of 1996 through the summer of 1997, the papers authors engaged in a project to verify the correctness of the Wildfire cache-coherence protocol and wrote an extremely sophisticated TLA+ specifications for the protocol and memory model.
Auxiliary paper
https://github.com/pron/wildfire-challenge/blob/master/Wildfire.tla
Auxiliary paper
(***************************************************************************)
(* MESSAGE SWITCHING ACTIONS *)
(* *)
(* The following actions are ones in which the LS just moves messages from *)
(* queue to queue. *)
(***************************************************************************)
LSForwardMsgsToProcs(ls, idx) ==
(*************************************************************************)
(* The action with which local Switch ls forwards the messages from *)
(* idx-th message set in Q.GSToLS[ls] to their destination processors *)
(* (and throws the Clears away). *)
(*************************************************************************)
/\ \E m \in Q.GSToLS[ls][idx] : m \notin Q0Message
/\ CanDequeueMsgSet("GSToLS", ls, idx)
/\ Q' = [Q EXCEPT
!.GSToLS[ls] = SeqMinusItem(@, idx),
!.LSToProc = [p \in Proc |->
LET
msgsToP ==
{m \in Q.GSToLS[ls][idx] : MsgDestination(m) = p}
IN
IF msgsToP # {}
THEN Append(@[p], msgsToP)
ELSE @[p]]]
/\ UNCHANGED << memDir, fillQ, aInt, procVars>>
LSForwardMsgsToGS(p, idx) ==
(*************************************************************************)
(* The action by which processor p's local switch forwards a message in *)
(* Q.ProcToLS[p], destined for another local switch, to the GS. The *)
(* message must be a Q0 message, since that's the only kind of messages *)
(* that originate at a processor. *)
(*************************************************************************)
/\ \E m \in Q.ProcToLS[p][idx] : MsgDestination(m) # ProcLS(p)
/\ CanDequeueMsgSet("ProcToLS", p, idx)
/\ Q' = [Q EXCEPT !.ProcToLS[p] = SeqMinusItem(@, idx),
!.LSToGS[ProcLS(p)] = Append(@, Q.ProcToLS[p][idx])]
/\ UNCHANGED << memDir, fillQ, aInt, procVars>>
-----------------------------------------------------------------------------
(***************************************************************************)
(* THE GS ACTION *)
(* *)
(* The GS is just a message switch. *)
(***************************************************************************)
GSForwardMsgsToLS(ls, idx) ==
(*************************************************************************)
(* The GS removes the idx-th message set from Q.LSToGS[ls] and transfers *)
(* its contents to the appropriate GSToLS queues. *)
(*************************************************************************)
/\ CanDequeueMsgSet("LSToGS", ls, idx)
/\ Q' = [Q EXCEPT
!.LSToGS[ls] = SeqMinusItem(@, idx),
!.GSToLS = [t \in LS |->
LET ms == {m \in Q.LSToGS[ls][idx] :
\/ MsgDestination(m) = t
\/ /\ MsgDestination(m) \in Proc
/\ ProcLS(MsgDestination(m)) = t}
IN IF ms = { } THEN Q.GSToLS[t]
ELSE Append(Q.GSToLS[t], ms)] ]
/\ UNCHANGED <<memDir, fillQ, procVars, aInt>>
-----------------------------------------------------------------------------
(***************************************************************************)
(* THE NEXT-STATE ACTION *)
(***************************************************************************)
Next ==
\/ \E p \in Proc :
\/ \E req \in Request : ProcReceiveRequest(p, req)
\/ \E idx \in DOMAIN respQ[p] : ProcSendResponse(p, idx)
\/ \E adr \in Adr : ProcEvictCacheLine(p, adr)
\/ \E idx \in DOMAIN Q.LSToProc[p] : ProcReceiveMsg(p, idx)
\/ \E m \in fillQ[p] : ProcReceiveFill(p, m)
\/ \E idx \in DOMAIN reqQ[p] : \/ ProcIssueDirReq(p, idx)
\/ ProcExecuteFromCache(p, idx)
\/ \E idx \in DOMAIN Q.ProcToLS[p] :
\/ LSForwardMsgsToGS(p, idx)
\/ LSReceiveRequestFromProc(p, idx)
\/ LSReceiveVictimFromProc(p, idx)
\/ \E ls \in LS :
\/ \E idx \in DOMAIN Q.GSToLS[ls] : LSReceiveRequestFromGS(ls, idx)
\/ \E idx \in DOMAIN Q.GSToLS[ls] : LSReceiveVictimFromGS(ls, idx)
\/ \E idx \in DOMAIN Q.GSToLS[ls] : LSForwardMsgsToProcs(ls, idx)
\/ \E idx \in DOMAIN Q.LSToGS[ls] : GSForwardMsgsToLS(ls, idx)
-----------------------------------------------------------------------------
(***************************************************************************)
(* THE COMPLETE TEMPORAL-LOGIC SPECIFICATION *)
(***************************************************************************)
Liveness ==
(*************************************************************************)
(* This is the specification's liveness condition. We want it to *)
(* guarantee that every request eventually generates a response. This *)
(* requires the processing of things sitting in queues--namely, requests *)
(* in the request queue, response in the response queue, and messages in *)
(* the various message queues. We don't require that queues be FIFO. *)
(* That is, we allow requests to be processed out of order, responses to *)
(* be delivered out of order, and messages to be delivered from a queue *)
(* out of order (subject to constraints, of course). However, we don't *)
(* require that things be processed out of order. For example, if the *)
(* message at the head of Q.LSToProc[p] is a ForwardedGet that p cannot *)
(* process because it doesn't yet have a copy of the data, we don't *)
(* require that other messages be processed before the ForwardedGet is. *)
(* We allow p to process no messages until it can process that *)
(* ForwardedGet. (See the discussion of shadowing in the comment for *)
(* the definition of InShadowMode.) Hence, we put a fairness condition *)
(* only on the processing of the first element of a queue. *)
(* *)
(* Remember that fillQ[p] is a set of Fills, not a queue. Hence, there *)
(* is no "first element". We require that any Fill in fillQ[p] must *)
(* eventually be received by processor p. *)
(* *)
(* In TLA, the formula WF_v(A) asserts that if action A /\ (v'#v) is *)
(* ever continuously enabled, then an A /\ (v'#v) step must eventually *)
(* occur. *)
(*************************************************************************)
/\ \A p \in Proc :
/\ WF_wVars((respQ[p] # <<>>) /\ ProcSendResponse(p, 1))
/\ WF_wVars((Q.LSToProc[p] # <<>>) /\ ProcReceiveMsg(p, 1))
/\ \A m \in Fill : WF_wVars( /\ m \in fillQ[p]
/\ ProcReceiveFill(p, m) )
/\ WF_wVars((reqQ[p] # <<>>) /\ ProcIssueDirReq(p, 1))
/\ WF_wVars((reqQ[p] # <<>>) /\ ProcExecuteFromCache(p, 1))
/\ WF_wVars((Q.ProcToLS[p] # <<>>) /\ LSForwardMsgsToGS(p, 1))
/\ WF_wVars((Q.ProcToLS[p] # <<>>) /\ LSReceiveRequestFromProc(p, 1))
/\ WF_wVars((Q.ProcToLS[p] # <<>>) /\ LSReceiveVictimFromProc(p, 1))
/\ \A ls \in LS :
/\ WF_wVars((Q.GSToLS[ls] # <<>>) /\ LSReceiveRequestFromGS(ls, 1))
/\ WF_wVars((Q.GSToLS[ls] # <<>>) /\ LSReceiveVictimFromGS(ls, 1))
/\ WF_wVars((Q.GSToLS[ls] # <<>>) /\ LSForwardMsgsToProcs(ls, 1))
/\ WF_wVars((Q.LSToGS[ls] # <<>>) /\ GSForwardMsgsToLS(ls, 1))
Spec == /\ Init
/\ [][Next]_wVars
/\ Liveness
-----------------------------------------------------------------------------
THEOREM Spec => [](TypeInvariant /\ MessageInvariant)
=============================================================================
Last modified on Sun Jun 18 09:38:33 PDT 2000 by lamportAWS decided to try TLA+
FIRST SUCCESS
DynamoDB launched in January 2012
Verified that a complex part of the algorithm was correct
Found a bug that could lead to dataloss if a perticular series of failures and recovery steps would be interleaved with other processing
very subtle bug
CONVINCE OTHER ENGINEERS
Testable Pseudo-code
MORE SUCCESS
Tweak specification to introduce optimizations
AWS management starts encouraging teams to adopts formal methods.
TLA+ model finds a known very subtle bug that passed through mutliple reviews in seconds.
ROBUSTNESS
SIDE BENEFIT
Great documentation
Confidence in changing a system
What are formal methods good for
Sustained emergent performance degradation
A slowdown on the server, perhaps due to a Java garbage collection causes timeouts to be breached on clients, causing clients to retry requests, thus adding load to the server, and further shutdowns.
not
How do we know that the executable code correctly implements the verified design?
We don't.
But formal methods help:
At least get the design right
Gain better understanding of the system
We have a what-if tool for designers
CONCLUSION
Improve the quality of products
Big Success at AWS
Caveats
Prevent subtle, serious bugs from reaching production. Bugs that we would not have found via any other technique.
Confidence to make aggressive optimizations to complex algorithms without sacrificing quality
Formal methods deal with models of systems, not the systems themselves
“All models are wrong, some are useful.”
Designer must ensure that the model captures the significant aspects of the real system.
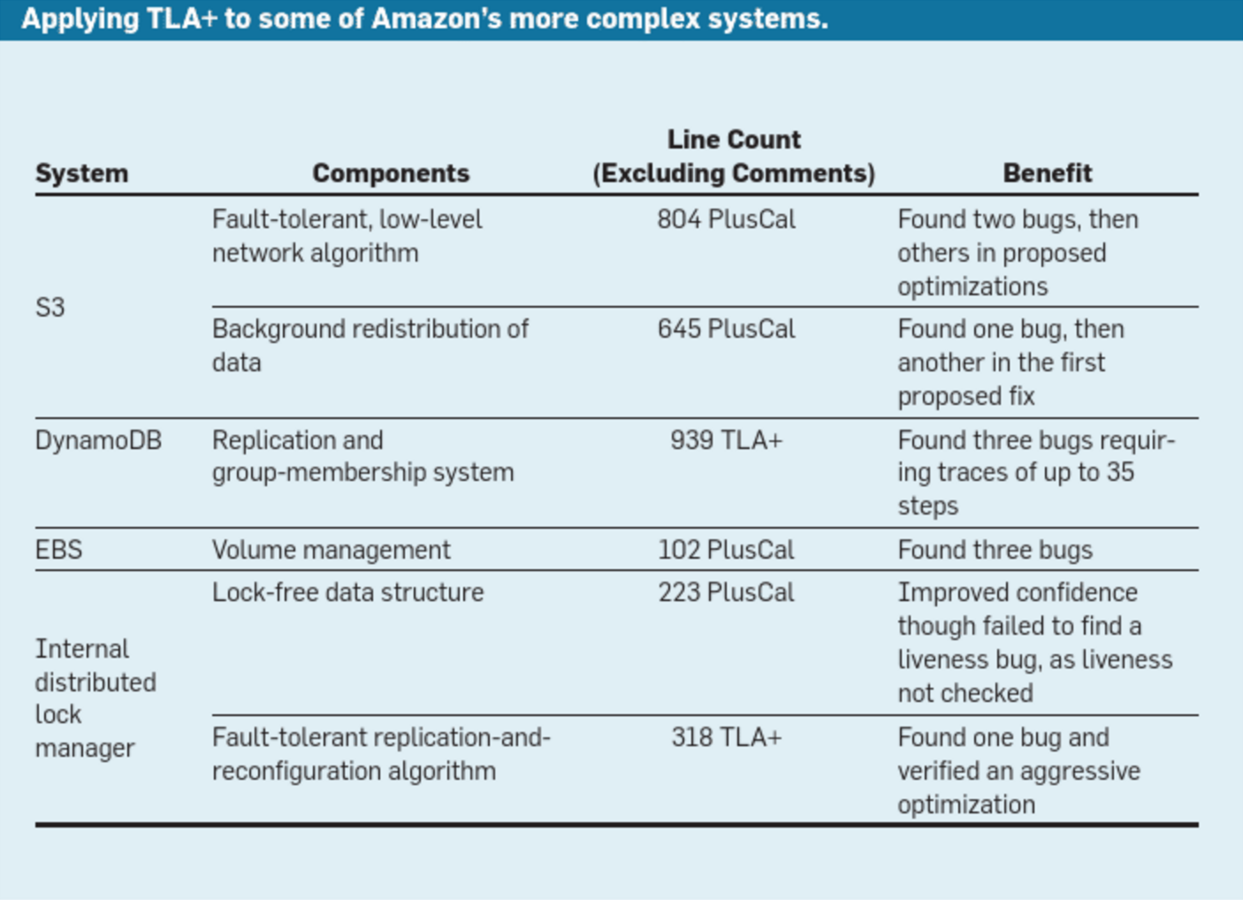
Review and reflection on the paper
The paper is well written and clearly documents the adoptions, use and success of formal methods within AWS.
The paper is important. It is one of the first documentations of adopting formal method for enterprise software development outside of critical-systems.
Too one-sided
QUESTIONS?
AWS Formal Methods Light
By Tryggvi Gylfason
AWS Formal Methods Light
- 919



