Balanced Binary
Search Tree
Agenda
- The target of Balanced Binary Search Tree
- Property
- Maintenance
- AVL Tree
- Red Black Tree (Brief)
- STL implemented Balanced Binary Search Tree
- stl set
- stl map
- (pbds)
Balanced Binary
Search Tree
Target
Recall Binary Search Tree
- Search : O(h)
- Insert : O(h)
- delete : O(h)
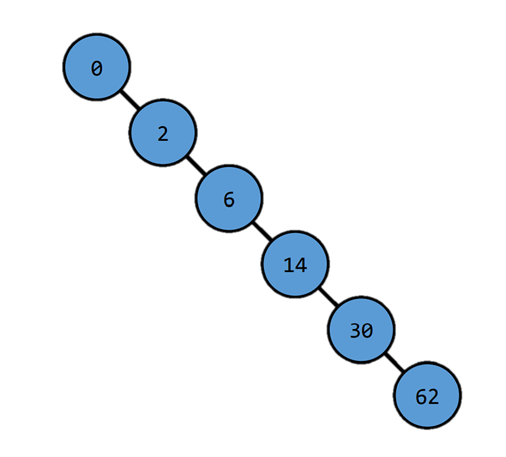
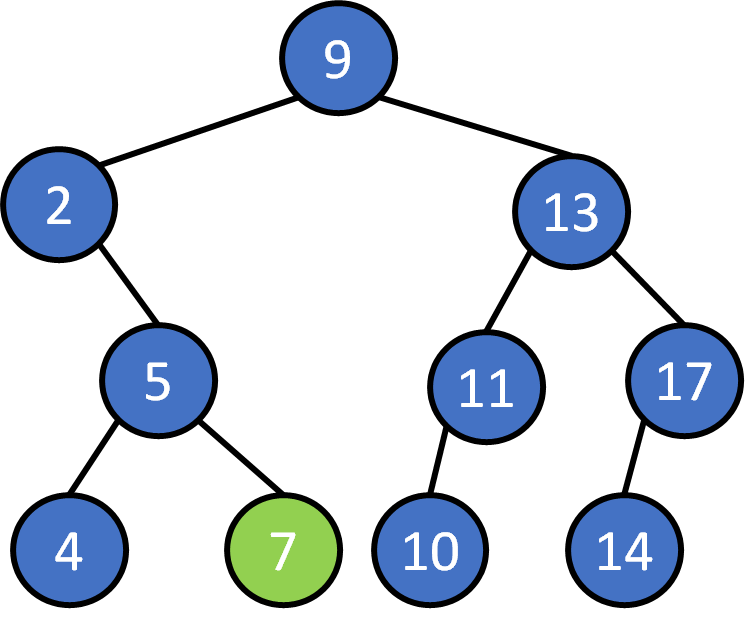
h : tree height
(both insert and delete requires one search operation)
What we hope
Can we keep the height in a certain range?
May require some clever operation
Balanced Binary Search Tree !
The height is in O(logN) !
May require some clever operation
named after inventors
Adelson-Velsky and Landis
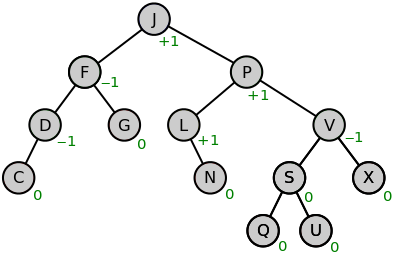
(這裡的BF跟本次定義的是反的)
BF(x) = hr(x) - hl(x)
但不影響
Some Definition
: Left Subtree
T_{l}
T_{r}
: Right Subtree
h
: Tree Height
h_{l}
: Left SubTree Height
h_{r}
: Right SubTree Height
BF(p)
: Balance Factor of node p
BF(p) = h_{l}(p) - h_{r}(p)
Definition Example
Q
M
P
S
N
R
h_{l}(Q) = 2\\
h_{r}(Q) = 1\\
BF(Q) = 1
h_{l}(M) = -1\\
h_{r}(M) = 1\\
BF(M) = -2
h_{l}(S) = -1\\
h_{r}(S) = 0\\
BF(S) = -1
BF(R) = 0
BF(P) = 1
BF(N) = 0
height of a leaf = 0
height of a null node = -1
AVL Tree
Property
A Tree is an AVL Tree if :
- Left Subtree and Right Subtree are also an AVL Tree
|h_{l} - h_{r}| \leq 1
(It's a recurrence definition !)
Text
An simple proof of AVL Tree height = O(logN)
AVL Tree Rebalance
Rotation
After some operation (insert / delete)
we may violate the property of AVL tree
we'll need to do sth. to maintain the AVL property.
Note that after the operation it should still be and Binary search tree
it's inorder shouldn't change
Left Rotation
50
60
Let's do left rotation on 50.
null
null
null
Left Rotation
50
60
Let's do right rotation on 50.
null
null
null
Note how the null ptr moves
do we still have BST property?
Left Rotation
50
60
if they're not null ptr
do we still have BST property?
(think about what value range is possible for each subtree.)
Left Rotation
50
60
if they're not null ptr
do we still have BST property?
(think about what value range is possible for each subtree.)
Right Rotation
60
70
Similiar to Left rotation
Right Rotation
60
70
do we still have BST property?
Left Rotation
Focus on the height changing
BF(p) > 1, hl > hr, needs Right rotation
BF(p) < -1, hl < hr, needs Left rotation
x
z
BF(x)=-2
h_{l}(x)=h
h_{r}(x)=h+2
x
z
BF(z)=-1
h
h
h
h
h+1
h_{l}(z)=h
h_{r}(z)=h+1
BF(x)=0
h_{l}(x)=h
h_{r}(x)=h
BF(z)=0
h_{l}(z)=h+1
h_{r}(z)=h+1
h+1
Right Rotation
Focus on the height changing
BF(p) > 1, hl > hr, needs Right rotation
BF(p) < -1, hl < hr, needs Left rotation
BF(x)=1
h_{l}(x)=h+1
h_{r}(x)=h
x
z
BF(z)=2
h
h
h_{l}(z)=h+2
h_{r}(z)=h
x
z
h
h
h+1
BF(x)=0
h_{l}(x)=h+1
h_{r}(x)=h+1
BF(z)=0
h_{l}(z)=h
h_{r}(z)=h
h+1
AVL Tree Rotation
Depends on the tree status,
we may have the following four type rotations
LL type
RR type
LR type
RL type
50
60
70
LL
50
60
70
RR
heavier: the tree with larger height.
LL type Rotation
LL type: do a right rotation on the pivot.
C
B
A
pivot
h
h
h
case (to pivot):
The left subtree is heavier.
and
The left subtree of
the left child is heavier.
i.e. i the one contribute
to
h_l(A) \text{ is }h_l(B)
BF(A)=2
BF(B)=1
<- WLOG
h-1
LL type Rotation
LL type: do a right rotation on the pivot.
C
B
A
pivot
h
h
h
case (to pivot):
The left subtree is heavier.
and
The left subtree of
the left child is heavier.
i.e. i the one contribute
to
h_l(A) \text{ is }h_l(B)
BF(A)=0
BF(B)=0
h-1
RR type Rotation
RR type: do a left rotation on the pivot.
C
B
A
pivot
h
h
h
case (to pivot):
The right subtree is heavier.
and
The right subtree of
the right child is heavier.
i.e. the one who contribute
to
h_r(A) \text{ is }h_r
(B)
BF(A)=-2
BF(B)=-1
h-1
A
B
C
pivot
h
h
h
BF(A)=0
BF(B)=0
h-1
RR type Rotation
RR type: do a left rotation on the pivot.
case (to pivot):
The right subtree is heavier.
and
The right subtree of
the right child is heavier.
i.e. the one who contribute
to
h_r(A) \text{ is }h_r
(B)
LR type Rotation
- LR type: first do a left rotation on the left child, then do a right rotation on the pivot.
C
B
A
pivot
h
h
h
case (to pivot):
The left subtree is heavier.
and
The right subtree of
the left child is heavier.
i.e. the one who contribute
to
h_l(A) \text{ is }h_r
(B)
BF(A)=2
BF(B)=-1
h-1
BF(C)=1(-1)
LR type Rotation
- LR type: first do a left rotation on the left child, then do a right rotation on the pivot.
C
B
A
pivot
h
h
h
case (to pivot):
The left subtree is heavier.
and
The right subtree of
the left child is heavier.
i.e. the one who contribute
to
h-1
BF(A)=2
BF(B)=0 (1)
BF(C)=2(1)
h_l(A) \text{ is }h_r
(B)
(it becomes an LL type !)
LR type Rotation
- LR type: first do a left rotation on the left child, then do a right rotation on the pivot.
C
B
A
pivot
h
h
h
case (to pivot):
The left subtree is heavier.
and
The right subtree of
the left child is heavier.
i.e. the one who contribute
to
h-1
BF(A)=-1(0)
BF(B)=0(1)
BF(C)=0
h_l(A) \text{ is }h_r
(B)
RL type Rotation
- RL type: first do a right rotation on the right child, then do a left rotation on the pivot.
C
B
A
pivot
h
h
h
case (to pivot):
The right subtree is heavier.
and
The left subtree of
the right child is heavier.
i.e. the one who contribute
to
h_r(A) \text{ is }h_l
(B)
BF(A)=-2
BF(B)=1
h-1
BF(C)=1(-1)
RL type Rotation
- RL type: first do a right rotation on the right child, then do a left rotation on the pivot.
C
B
A
pivot
h
h
h
case (to pivot):
The right subtree is heavier.
and
The left subtree of
the right child is heavier.
i.e. the one who contribute
to
h_r(A) \text{ is }h_l
(B)
BF(A)=-2
BF(B)=1
h-1
BF(C)=-1(-2)
(it becomes an RR type !)
RL type Rotation
- RL type: first do a right rotation on the right child, then do a left rotation on the pivot.
C
B
A
pivot
h
h
h
case (to pivot):
The right subtree is heavier.
and
The left subtree of
the right child is heavier.
i.e. the one who contribute
to
h_r(A) \text{ is }h_l
(B)
BF(A)=0(1)
BF(B)=1(0)
h-1
BF(C)=0
LL type Rotation
LL type: do a right rotation on the pivot.
pivot
50
60
70
RR type Rotation
RR type: do a left rotation on the pivot.
pivot
50
60
70
RR type Rotation
RR type: do a left rotation on the pivot.
pivot
50
60
70
- LR type: first do a left rotation on the left child, then do a right rotation on the pivot.
LR type Rotation
50
60
70
pivot
- LR type: first do a left rotation on the left child, then do a right rotation on the pivot.
LR type Rotation
50
60
70
pivot
left rotation on 50
(it becomes a LL type)
- LR type: first do a left rotation on the left child, then do a right rotation on the pivot.
LR type Rotation
50
60
70
pivot
left rotation on 50
right rotation on 70
- RL type: first do a right rotation on the right child, then do a left rotation on the pivot.
RL type Rotation
80
90
70
pivot
- RL type: first do a right rotation on the right child, then do a left rotation on the pivot.
RL type Rotation
80
90
70
pivot
right rotation on 90
- RL type: first do a left rotation on the right child, then do a right rotation on the pivot.
RL type Rotation
80
90
70
pivot
right rotation on 90
left rotation on 70
Insertion/Delete
Rebalancing
(這裡的BF跟本次定義的是反的)
BF(x) = hr(x) - hl(x)
但不影響
Insert/Delete
The first step acts just like binary search tree insertion and deletion
Insert
1. insert the node at desired leaf position
Delete
1. Find the node
2. replace the node with
{the largest if left subtree / the smallest in right subtree}
!?
The problem is that after insert/delete, the tree may become unbalanced.
We have to rebalance it by previous operations !
Insert Rebalancing
Strategy
Resolve unbalanced ancestors of the new node.
from parent to root
\text{unbalanced} := |BF(p)| \gt 1
Think about why we use this strategy.
(Recall AVL Tree defition)
Insert Rebalancing
\text{unbalanced} := |BF(p)| \gt 1
Think about why we use this strategy.
(Recall AVL Tree defition)
Strategy
Resolve unbalanced ancestors of the new node.
from parent to root
When we insert/delete a new node p, it must be a leaf.
Only the Balanced Factor of nodes with p in their subtree may be altered.
Insert Rebalancing
Strategy to resolve
if BF(p) = 2 (its left subtree is heavier)
check if BF(p's left child) = -1
yes -> do LR operation
no -> do LL operation
else if BF(p) = -2 (its right subtree is heavier)
check if BF(p's right child) = -1
yes -> do RR operation
no -> do RL operation
(is it possible to have BF(p) > 2 or BF(p) < -2 during insertion/deletion ? )
Example
80
90
70
50
75
Suppose insert 85
(click this)
BF = -1
Unbalanced!
BF = 0
BF = 0
BF = 0
BF = 0
85
BF = 0
Example
80
90
70
50
75
Suppose insert 85
85
BF = -2
BF = -1
BF = -1
BF = 0
BF = 0
BF = 0
Example
80
90
70
50
75
Suppose insert 85
BF = -2
BF = -1
BF = -1
BF = 0
BF = 0
85
BF = 0
Example
80
90
70
50
75
Suppose insert 85
85
BF = -2
BF = -1
BF = -1
BF = 0
BF = 0
Need which rotation?
(click)
RR rotation
BF = 0
Example
80
90
70
50
75
Suppose insert 85
BF = 0
BF = 0
BF = 1
BF = 0
BF = 0
Need which rotation?
RR rotation
85
BF = 0
Example
Mary
BF=0
Mary
BF=0
Example
Mary
BF=-1
May
BF=0
Example
May
BF=-1
Mary
BF=-2
Mike
BF=0
Rebalance !
(which? click me)
RR
Example
May
BF=0
Mary
BF=0
Mike
BF=0
Rebalance !
RR
Example
May
BF=1
Mary
BF=1
Mike
BF=0
Devin
BF=0
Example
May
BF=2
Mary
BF=2
Mike
BF=0
Devin
BF=1
Bob
BF=0
Rebalance !
(which? click me)
LL
Example
May
BF=1
Mary
BF=0
Mike
BF=0
Devin
BF=0
Bob
BF=0
Rebalance !
LL
Example
May
BF=2
Mary
BF=1
Mike
BF=0
Devin
BF=-1
Bob
BF=0
Jack
BF=0
Rebalance !
(which? click me)
LR
Example
May
BF=2
Mary
BF=2
Mike
BF=0
Devin
BF=0
Bob
BF=0
Jack
BF=0
Rebalance !
LR step1
Example
May
BF=-1
Mary
BF=0
Mike
BF=0
Devin
BF=0
Bob
BF=0
Jack
BF=0
Rebalance !
LR step 2
Example
May
BF=-1
Mary
BF=1
Mike
BF=0
Devin
BF=-1
Bob
BF=0
Jack
BF=1
Helen
BF=0
Example
May
BF=-1
Mary
BF=1
Mike
BF=0
Devin
BF=-1
Bob
BF=0
Jack
BF=0
Helen
BF=0
Joe
BF=0
Example
May
BF=-1
Mary
BF=2
Mike
BF=0
Devin
BF=-2
Bob
BF=0
Jack
BF=1
Helen
BF=-1
Joe
BF=0
Ivy
BF=0
Rebalance !
(which? click me)
RL
Example
May
BF=-1
Mary
BF=2
Mike
BF=0
Devin
BF=-2
Bob
BF=0
Jack
BF=-1
Helen
BF=-1
Joe
BF=0
Ivy
BF=0
Rebalance !
RL step1
Example
May
BF=-1
Mary
BF=1
Mike
BF=0
Devin
BF=1
Bob
BF=0
Jack
BF=0
Helen
BF=0
Joe
BF=0
Ivy
BF=0
Rebalance !
RL step2
Example
May
BF=-1
Mary
BF=2
Mike
BF=0
Devin
BF=1
Bob
BF=0
Jack
BF=-1
Helen
BF=-1
Joe
BF=-1
Ivy
BF=0
John
BF=0
Rebalance !
(which? click me)
LR
Example
May
BF=-1
Mary
BF=2
Mike
BF=0
Devin
BF=1
Bob
BF=0
Jack
BF=1
Helen
BF=1
Joe
BF=-1
Ivy
BF=0
John
BF=0
Rebalance !
LR step1
Example
May
BF=-1
Mary
BF=0
Mike
BF=0
Devin
BF=1
Bob
BF=0
Jack
BF=0
Helen
BF=1
Joe
BF=-1
Ivy
BF=0
John
BF=0
Rebalance !
LR step2
Example
May
BF=-2
Mary
BF=-1
Mike
BF=-1
Devin
BF=1
Bob
BF=0
Jack
BF=-1
Helen
BF=1
Joe
BF=-1
Ivy
BF=0
John
BF=0
Peter
BF=0
Rebalance !
(which? click me)
RR
Example
May
BF=0
Mary
BF=0
Mike
BF=0
Devin
BF=1
Bob
BF=0
Jack
BF=0
Helen
BF=1
Joe
BF=-1
Ivy
BF=0
John
BF=0
Rebalance !
RR
Peter
BF=0
Example
May
BF=0
Mary
BF=0
Mike
BF=0
Devin
BF=1
Bob
BF=0
Jack
BF=0
Helen
BF=1
Joe
BF=-1
Ivy
BF=0
John
BF=0
Peter
BF=0
Tom
BF=0
Analysis
| Operation | Sequential list | Linked list | AVL Tree |
|---|---|---|---|
| Search for element with key k | O(log n) (presorted) | O(n) | O(log n) |
| Search for j-th item | O(1) | O(j) | O(log n) |
| Delete element with key k | O(n) | O(1) | O(log n) |
| Delete j-th element | O(n-j) | O(j) | O(log n) |
| Insert | O(n) | O(1) | O(log n) |
| Output in order | O(n) | O(n) | O(n) |
Red Black Tree
Another efficient binary search tree
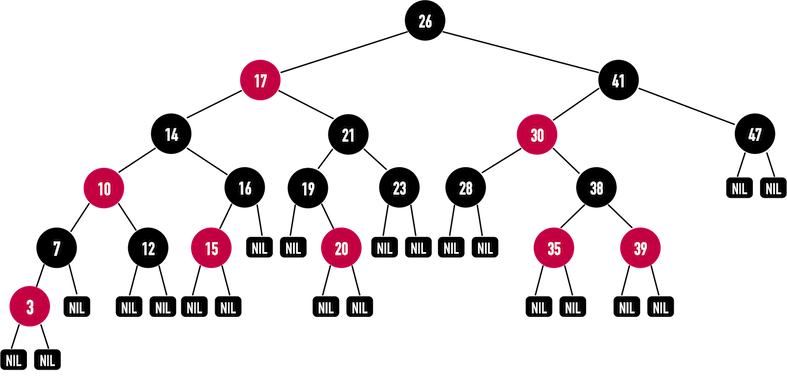
Definition
- The root and all external nodes are colored in black.
- No root-to-external-node path has two consecutive red nodes.
- All root-to-external-node paths have the same number of black nodes.
external nodes: the null pointer of leaf's child.
Resources
Red Black Tree: Intro(簡介) (alrightchiu.github.io)
NTHU Prof. Hon. (One of the best teachers in NTHU) - RedBlackTree (nthu.edu.tw)
standard library of C++
Usage
#include <set>
using namespace std;- Insert O(lgn)
- find O(lgn) (find the element)
- lower_bound (find 1st >= val)
- upper_bound (find 1st > val)
- erase O(lgn)
- Iterating O(lgn)
int main(){
set<int> S;
S.insert(89);
S.insert(36);
S.insert(25);
S.insert(44);
S.insert(27);
S.emplace(22);
return 0;
}iterating
int main(){
set<int> S;
/* some more insert */
set<int>::iterator it;
for(it = S.begin(); it!=S.end(); it++){
cout << *it << " ";
}
cout << endl;
return 0;
}22 25 27 36 44 89
set<int> S {14, 84, 17, 62, 33};
set<int>::iterator it;
for(it = S.begin(); it!=S.end(); it++)
cout << *it << " ";
cout << endl;
S.erase(84);
S.erase(17);
S.erase(417); // won't affect since there's no element.
for(it = S.begin(); it!=S.end(); it++)
cout << *it << " ";
cout << endl;
14 17 33 62 84
14 33 62
find & erase
set<int> S {14, 84, 17, 62, 33};
set<int>::iterator it = S.find(14);
if(it != S.end()) S.erase(it);
for(it = S.begin(); it!=S.end(); it++)
cout << *it << " ";
cout << endl;17 33 62 84
Note that the iterator can't be dereferenced or increased (it++) after an erase. Or it will cause a reference error.
lower_bound(>=)
upper_bound(>)
set<int> S {14, 84, 17, 62, 33};
set<int>::iterator it = S.lower_bound(42);
if(it != S.end()) cout << *it << " ";
it = S.lower_bound(17);
if(it != S.end()) cout << *it << " ";
it = S.upper_bound(17);
if(it != S.end()) cout << *it << " ";
cout << endl;17 33 62 84
It find the first element larger (or equal ) to the value.
62 17 33
It find the first element larger (or equal ) to the value.
If not exist, returns S.end().
Some notes
set<int> S {14, 84, 17, 62, 33};
set<int>::iterator it;
S.insert(25);
S.insert(19);
S.insert(17);
S.insert(62);
for(it = S.begin(); it!=S.end(); it++)
cout << *it << " ";
cout << endl;Be careful: std::set doesn't store duplicate value element.
See the example below.
If you want duplicate elements, use std::multiple_set.
All operations are similar to std::set
14 17 19 25 33 62 84
count
set<int> S {14, 84, 17, 62, 33};
set<int>::iterator it;
S.insert(25);
S.insert(19);
S.insert(17);
S.insert(62);
cout << S.count(25) << " ";
cout << S.count(23) << " ";
cout << S.count(17) << "\n";Be careful: std::set doesn't store duplicate value element.
See the example below.
If you want duplicate elements, use std::multiset.
All operations are similar to std::set
1 0 1
count
multiset<int> S {14, 84, 17, 62, 33};
S.emplace(25)
S.emplace(17);
S.emplace(17);
S.insert(25);
S.insert(19);
S.insert(17);
S.insert(62);
multiset<int>::iterator it;
cout << S.count(17) << " ";
cout << S.count(25) << " ";
cout << S.count(33) << "\n";set::multiset
4 2 1
standard library of C++
Similar to set, but each node is a pair
stores (key, value)
use key to search and get value.
Usage
#include <map>
using namespace std;- Insert O(lgn)
- find (accessing) O(lgn) (find the element)
- lower_bound (find 1st >= val)
- upper_bound (find 1st > val)
- delete O(lgn)
- Iterating O(lgn)
Insert
map<int, int> M;
M.insert(pair<int,int>(25, 13));
M.insert(pair<int,int>(17, 12));
M[99] = 1;
M.emplace(62, 14);iterating
map<char, int> M;
M.insert(pair<char,int>('A', 13));
M.insert(pair<char,int>('E', 12));
M['U'] = 1;
M.emplace('N', 14);
map<char, int>::iterator it;
for(it = M.begin(); it!=M.end(); it++)
cout << "(" << it->first << ", " << it->second << ") ";
cout << endl;(A, 13) (E, 12) (N, 14) (U, 1)
accessing (lgn)
map<char, int> M;
M.insert(pair<char,int>('A', 13));
M.insert(pair<char,int>('E', 12));
M['U'] = 1;
M.emplace('N', 14);
cout << M['A'] << endl;
cout << M['K'] << endl; // cause error ?13
0
When using A['U'], the process is something like
- find that element
- if not exist, create it using the default constructer on its value
- return the r-value of the element
delete
map<char, int> M;
M.insert(pair<char,int>('A', 13));
M.insert(pair<char,int>('E', 12));
M['U'] = 1;
M.emplace('N', 14);
map<char, int>::iterator it;
for(it = M.begin(); it!=M.end(); it++)
cout << "(" << it->first << ", " << it->second << ") ";
cout << endl;
M.erase('E');
M.erase('K'); // won't affect
for(it = M.begin(); it!=M.end(); it++)
cout << "(" << it->first << ", " << it->second << ") ";
cout << endl;
(A, 13) (E, 12) (N, 14) (U, 1)
(A, 13) (N, 14) (U, 1)
find & delete
map<char, int> M;
M.insert(pair<char,int>('A', 13));
M.insert(pair<char,int>('E', 12));
M['U'] = 1;
M.emplace('N', 14);
map<char, int>::iterator it;
it = M.find('N');
M.erase(it);
/*
it = M.find('K');
M.erase(it); // cause error
*/
for(it = M.begin(); it!=M.end(); it++)
cout << "(" << it->first << ", " << it->second << ") ";
cout << endl;17 33 62 84
Note that the iterator can't be dereferenced or increased (it++) after an erase. Or it will cause a reference error.
lower_bound(>=)
upper_bound(>)
map<int, int> M = {{22,7 }, {14, 8}, {97, 42}, {2, 144}};
map<int, int>::iterator it;
it = M.lower_bound(98);
if(it != M.end())
cout << it->second << " ";
it = M.lower_bound(14);
if(it != M.end())
cout << it->second << " ";
it = M.upper_bound(14);
if(it != M.end())
cout << it->second << " ";It find the first element larger (or equal ) to the value.
If not exist, returns S.end().
8 7 ⏎
Some notes
Be careful: std::map doesn't store duplicate value element.
If you want duplicate elements, use std::multimap.
All operations are similar to std::map
Balanced Binary Search Tree
By tunchin kao
