演算法競賽概述

給你一個問題

計算特定數值下的
答案是多少

設計出一個演算法
能夠計算出那種問題在各種情況下的解

為何選擇C/C++

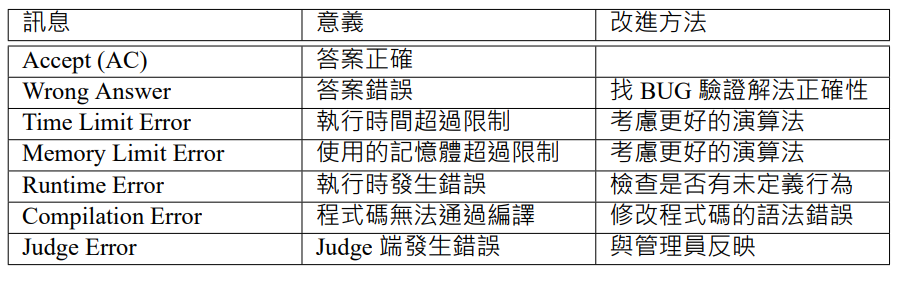
解讀錯誤訊息

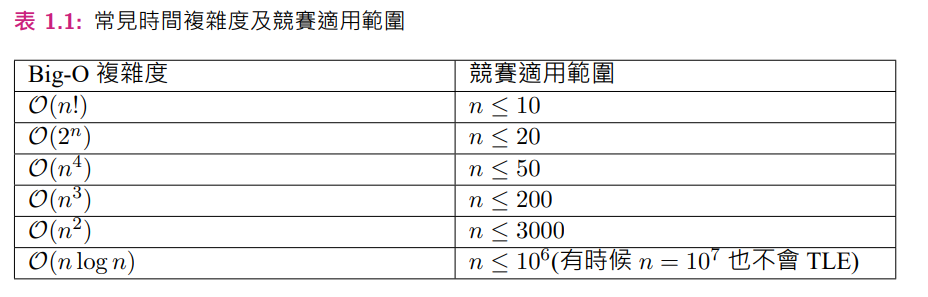
時間分析

一個有經驗的選手在看到題目後會怎麼做

對於一個演算法
除了正確性之外
他的效率也是我們考量的重點

衡量一下
一個演算法會執行多少次基本運算
(+, -, *, /, [], =)

for(int i = 0; i < n; i++) {
  for(int j = 0; j < n; j++) {
    cout << i << ' ' << j << '\n';
  }
}
//
for(int i = 0; i < n; i++) {
  cout << i << '\n';
}
for(int j = 0; j < n; j++) {
  cout << j << '\n';
}

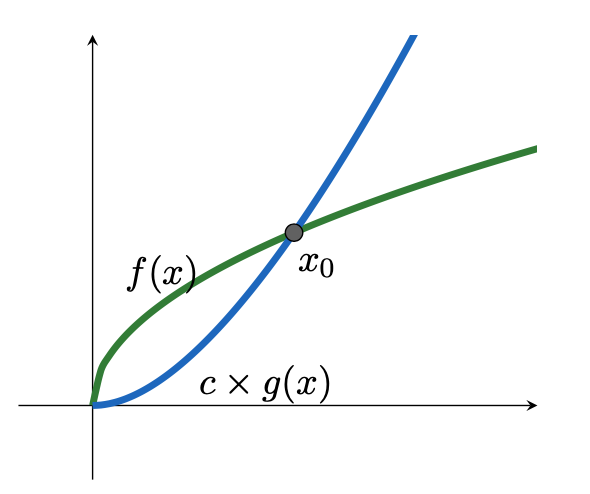
時間複雜度

x \geq x_0

簡單來說：
計算一個演算法會需要做多少次基本運算
並取其影嚮力最大的項

f(n) = 2n^3 + 3n^2 + 6n + 7
O(f(x)) \in O(n^3)
for(int i = 0; i < n; i++) {
  for(int j = i; j < n; j++) {
    cout << i << ' ' << j << '\n';
  }
}
n + (n - 1) + .... + 1 = \frac{(1 + n) * n}{2} = \frac{n}{2} + \frac{n^2}{2}
O(n^2)

僅供參考

基本語法知識

Undefined behavior

cout << 1/0 << '\n';
int x; cin >> x; //input = INT_MAX
if(x + 1 > x) {
  cout << "x + 1 > x\n";
} else {
  cout << "x + 1 <= x\n";
}
cout << x + 1 << ' ' << x << '\n';

C++字串

真香，用過就回不去C-style string了

浮點數誤差

常見輸入輸出

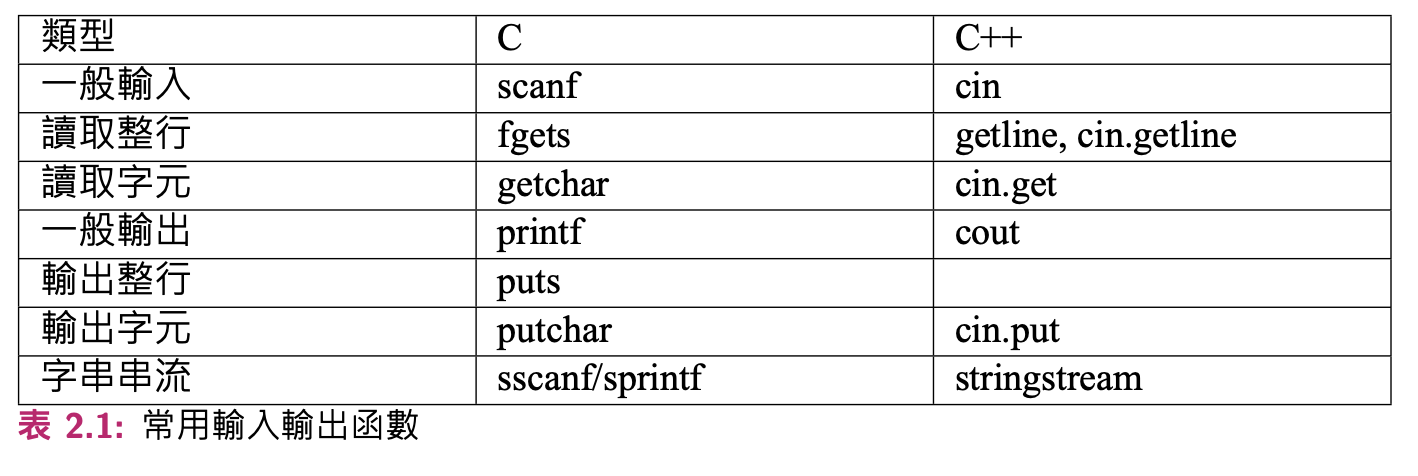
C++ 的 IO 優化

避免使用endl

避免混用C/C++的IO

cin.tie(0);
ios_base::sync_with_stdio(0);

C++的輸出入cin/cout和scanf/printf誰比較快？ | Chino's

簡單STL工具介紹

更多的內容會在其他課程中提到

pair

vector

動態大小的陣列
Capacity(容量) vs Size(大小)

擴增一次容量需要開一個新的陣列並將舊的元素全部搬過去

emplace_back vs push_back

push_back 是建構一個臨時的物件再將他複製到尾端

emplace_back 直接呼叫建構子建構在尾端

大部分時候emplace_back的效率優於push_back

vector<pair<int,int>> v; //C++11 以前 > >

v.push_back(make_pair(1, 2));
v.push_back({1, 2}); //C++11

v.emplace_back(1, 2);

題外話

C++ 對於每種基本的資料型態(int, long long)，沒有規定其確切的 byte數量，僅有規定其至少要有幾個byte以及之間的大小關係，如 long >= int。

明明bool只需要表示0, 1為什麼需要1 Byte?

bitset

其他常見小技巧

while(x --> 0) {

}

while(x-- > 0) {

}

while(x--) {

}

全域變數

系統在分配記憶體空間時，給區域變數的空間會比全域的小，儘管你宣告的區域變數的大小沒有超過記憶體空間上限，仍然會造成程式錯誤。

把數量級不小的陣列都開在全域

型態轉換

重新定義型別名

auto

reference

幫變數取別名

int a = 3;
int& b = a;
b = 4;
a = 5;
swap(int *a, int *b) {
  int tmp = *a;
  *a = *b;
  *b = tmp;
}
swap(&a, &b);

swap(int &a, int &b) {
  int tmp = a;
  a = b;
  b = tmp;
}

Ranged-based for

vector<int> v(10, 7122);

for(auto it = v.begin(),ed=v.end(); it!=ed; it++) {
  int val = *it;
  ...
}
for(size_t i = 0; i < v.size(); i++) {
  int val = v[i];
  ...
}
for(int val : v) {
  ...
}

Ranged-based for

vector<int> v(10, 7122);

for(auto& val : v) {

}

include 所有 Library

基本技巧

遞迴

河內塔

有三根杆子A,B,C，A杆上有N個穿孔圓盤，盤的尺寸由下到上依次變小，要求按下列規則將所有圓盤移到C杆

  1. 每次只能移動一個圓盤
  2. 大盤不能疊在小盤上面

方便起見，盤子的編號由小到大/由上到下依序為 1 ~ N

河內塔

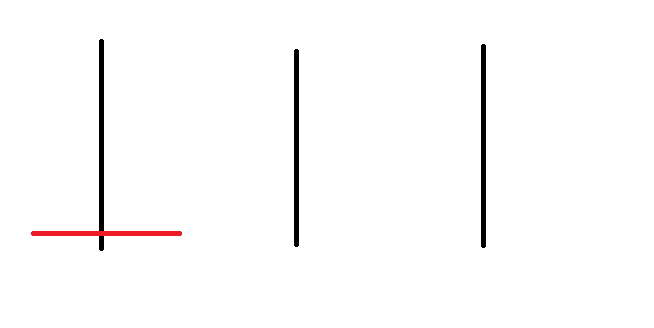
河內塔

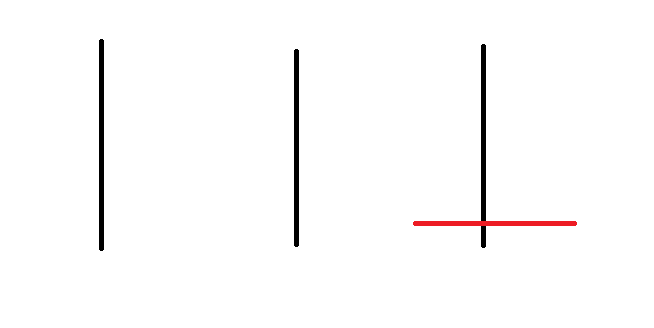
河內塔

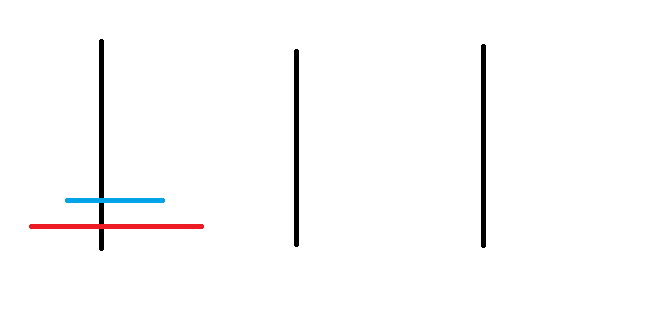
河內塔

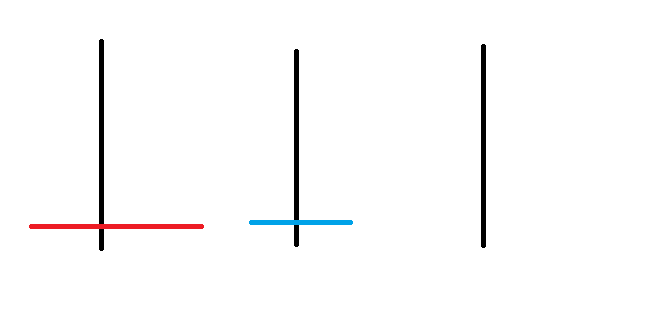
河內塔

河內塔

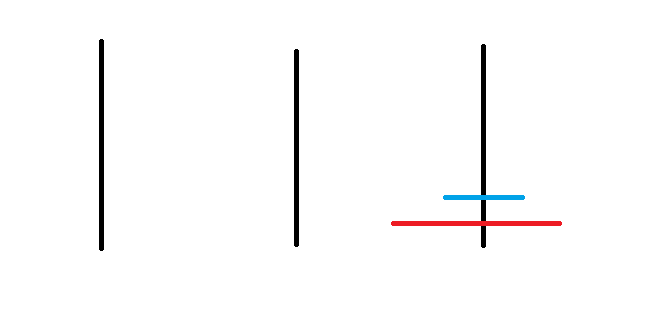
河內塔

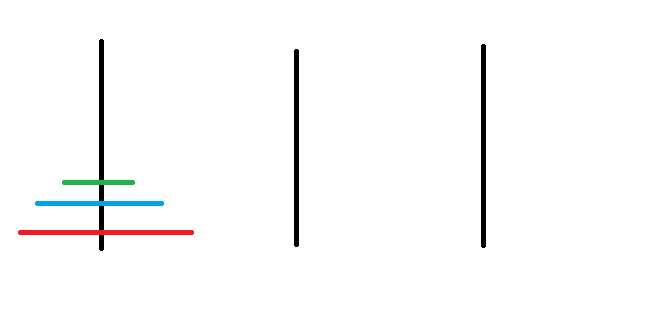
河內塔

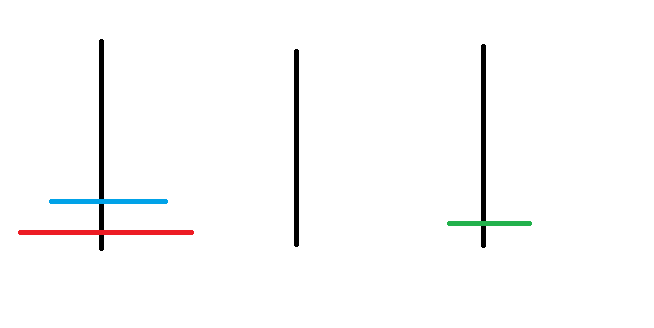
河內塔

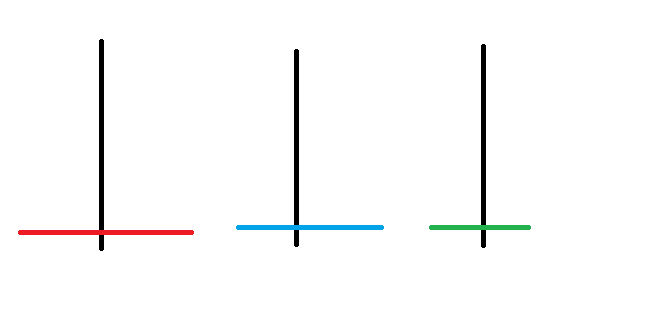
河內塔

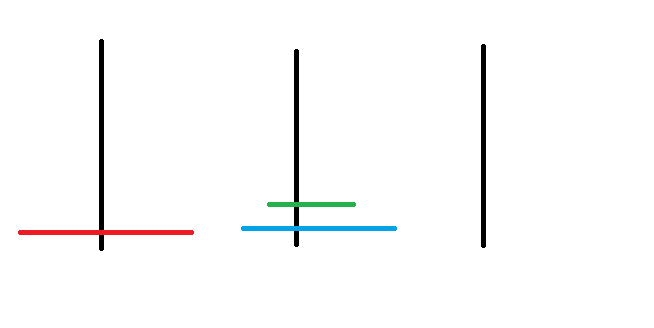
河內塔

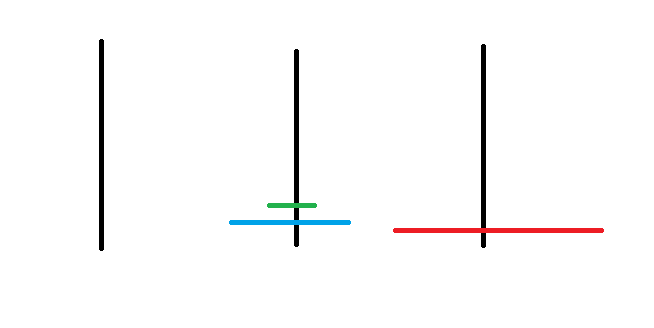
河內塔

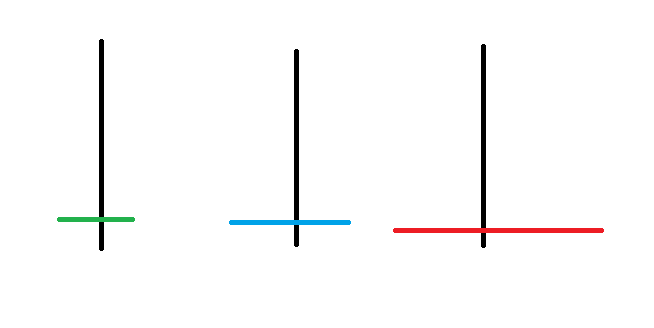
河內塔

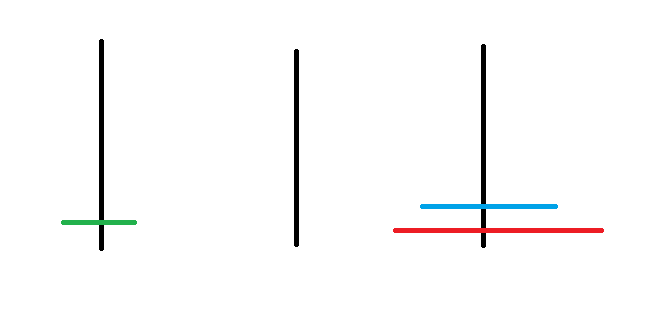
河內塔

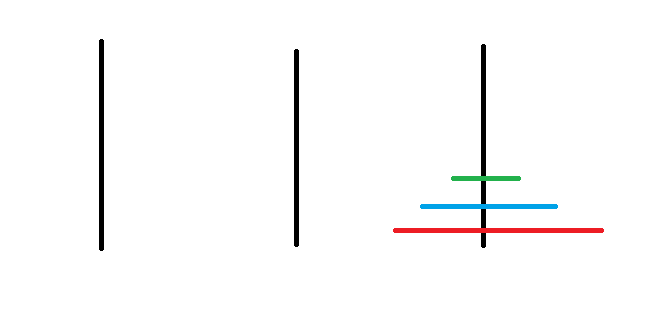
河內塔

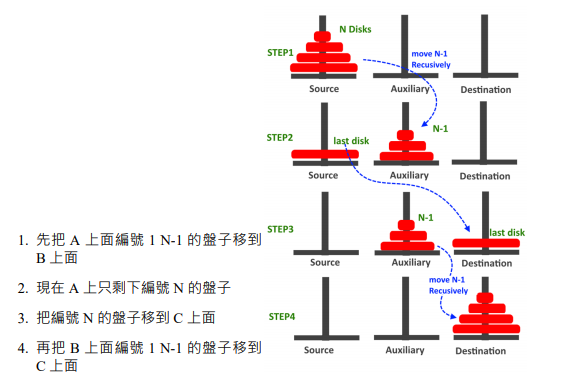
河內塔

#include<cstdio>
void hannoi(int n, char A, char B, char C) {
  if ( n == 0 ) return;
  hannoi(n-1, A, C, B);
  printf("Move ring %d from %c to %c\n", n, A, C);
  hannoi(n-1, B, A, C);
}
int main() {
  int n;
  while (scanf("%d", &n) != EOF) {
    hannoi(n, 'A', 'B', 'C');
  }
}

快速冪

樸素做法

int power(int a, int b) {
  int res = 1;
  for (int i = 0; i < b; i++) {
    res *= a;
  }
  return res;
}
a^b = a \times a^{b - 1}
a^b = {a^{\frac{b}{2}}}^2 
int power(int a, int b) {
  if (b == 0) return 1;
  if (b % 2) return a * power(a, b - 1);
  return power(a, b / 2) * power(a, b / 2);
}

這樣的時間複雜度？

將重複的值存起來

int power(int a, int b) {
  if (b == 0) return 1;
  if (b % 2) return a * power(a, b - 1);
  int tmp = power(a, b / 2);
  return tmp * tmp;
}


int power(int a, int b){
  return (b == 0 ?　1 : power(a * a, b/2) * (b & 1 ? a : 1));
}

非遞迴版本

int power(int a, int b) {
  int res = 1;
  while (b) {
    if (b & 1) res *= a;
    a *= a;
    b >>= 1;
  }
  return res;
}

cmath-pow

pow(2, 0.3333333)

最大公因數

枚舉因數

int gcd(int a, int b) {
  for (int i = min(a, b); i >= 2; i--) {
    if (a % i == 0 && b % i == 0) return i;
  }
  return 1;
}

輾轉相除法

int gcd(int a, int b) {
  if (a > b) swap(a, b);
  if (b % a == 0) return a;
  return gcd(a, b - a);
}

兩個整數的最大公因數等於
「其中較小的數和兩數的差的最大公因數」

將減法換成取模

int gcd(int a, int b) {
  return b == 0 ? a : gcd(b, a % b);
}

這樣的時間複雜度？

a \mod b < \frac{a}{2}
a \mod b < b
a \mod b \leq a - b

常見排序

Merge Sort

Divide

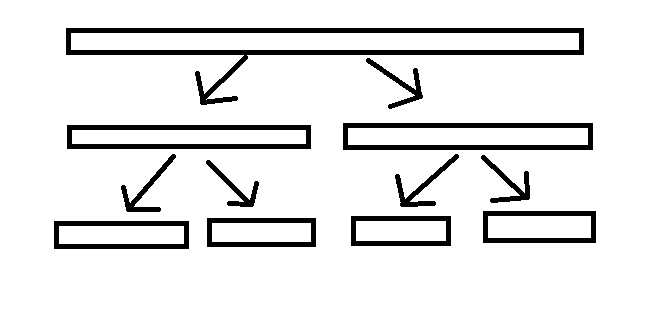
分 治 (Divide and Conquer)

Merge Sort

Conquer

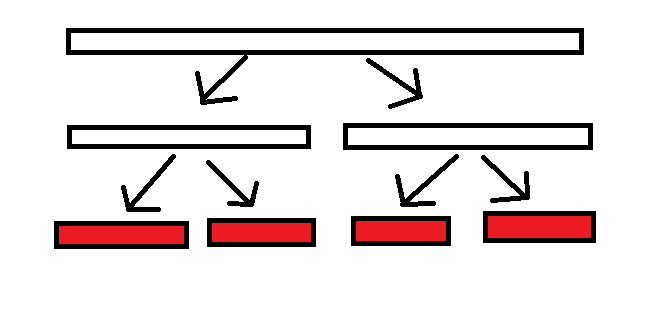
Merge Sort

Combine

use two pointer

Quick Sort

選定基準

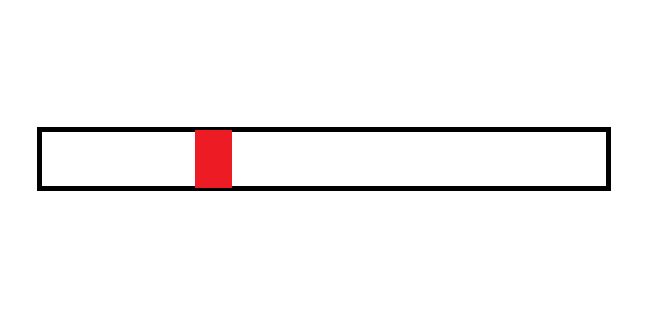
Quick Sort

小於基準的放左邊、大於的放右邊

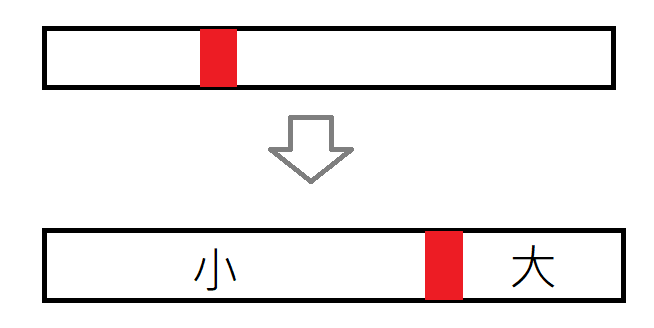
Counting Sort

計算每個數字出現次數，
再一個一個塞回序列當中。

std:sort

真香，不用嗎？

int a[N];
vector<string> v(n);
bool cmp(int a, int b) {
  return a > b;
}
sort(a, a + n);
sort(a, a + n, cmp);
sort(v.begin(), v.end());
sort(v.begin(), v.end(), [](string x, string y){
  return x > y;
})

暴力枚舉

暴力枚舉

給定 N(N ≤ 100) 根棒子，從中取出三根組成的所有三角形中，最大的周長多少?

八皇后問題

在N X N的棋盤上擺N隻皇后

請問有多少擺法使的N隻皇后不會互吃？

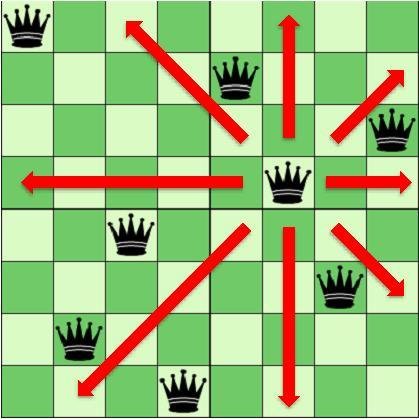
八皇后問題

深度優先搜尋

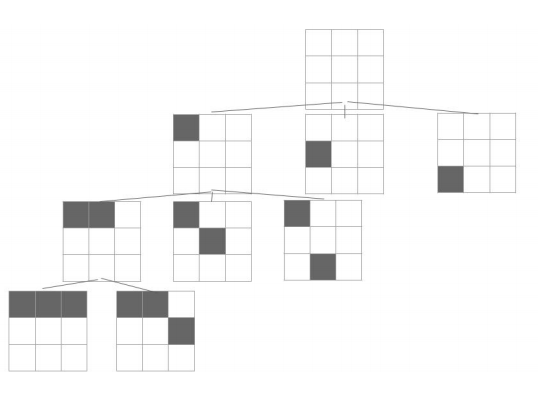
八皇后問題

剪枝

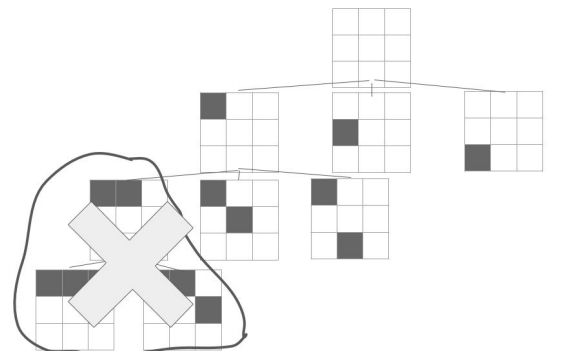
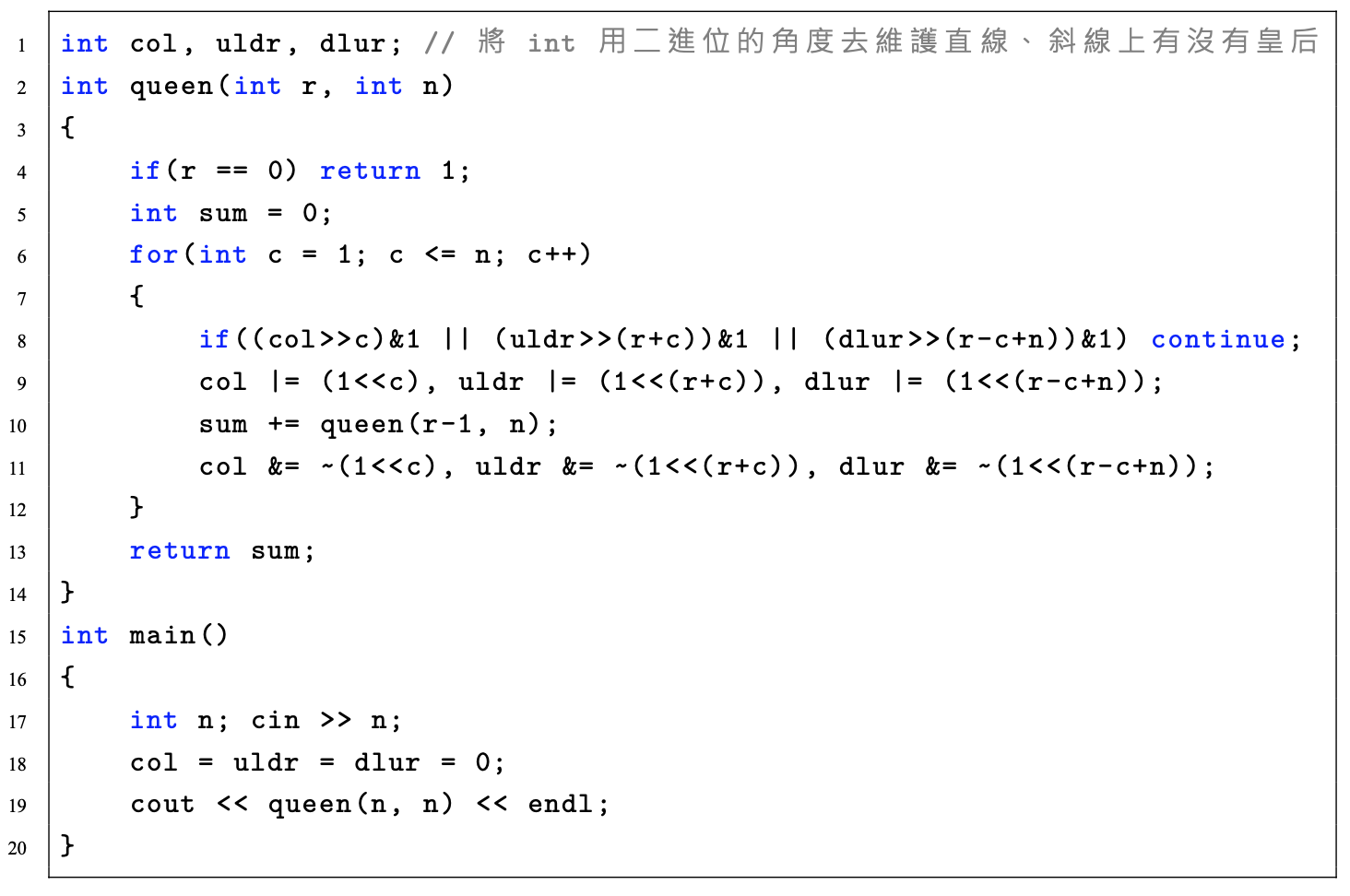
枚舉排列組合

遞迴大法好

枚舉不重複排列

int arr[] = { /* n項、已經由小到大排序 */ };
do {
    for (int i = 0; i < n; i++)
        cout << arr[i] << " ";
    cout << endl;
} while (next_permutation(arr, arr+n));

枚舉子集

枚舉集合
使用 bitset or 整數型態

1 0 1 1 0 0

0：不在集合裡

1：　在集合裡

枚舉所有子集

000
001

010

011

100

101

110

111

2^n

枚舉所有子集

for(int i = 0; i < (1 << n); i++) {
  ....
}

二分搜尋法

找遞增數列中x的位置

二分搜尋法

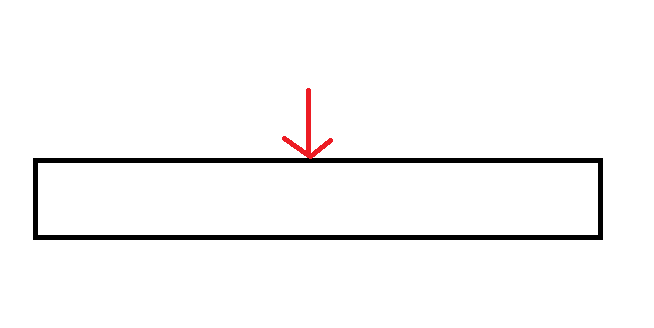
二分搜尋法

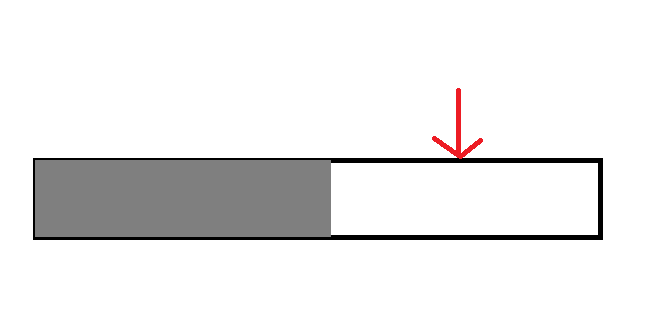
二分搜尋法

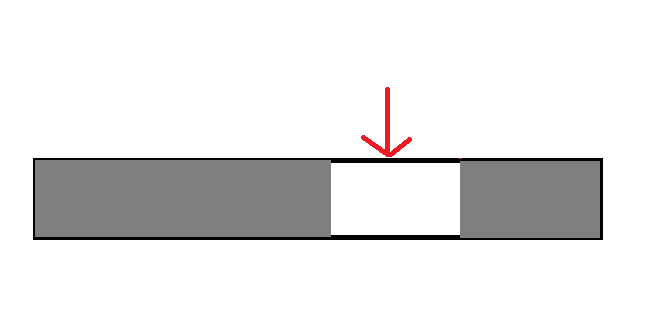
二分搜尋法

int bsearch(int *arr, int n, int x) {
  int l = 0, r = n-1, mid, ans = -1;
  while(l <= r) {
    mid = (l+r)/2;
    if(arr[mid] == x) {
      ans = mid; break;
    }
    if(arr[mid] < x) l = mid+1;
    else r = mid-1;
  }
  return ans;
}

STL的二分搜

對答案二分搜

若半徑R能滿足需求那所有大於R的也都能滿足需求

要怎麼判斷某半徑R是否能滿足需求

三分搜尋法

對於一個U型函數
要找出其最小值為何
也就是最低點

三分搜尋法

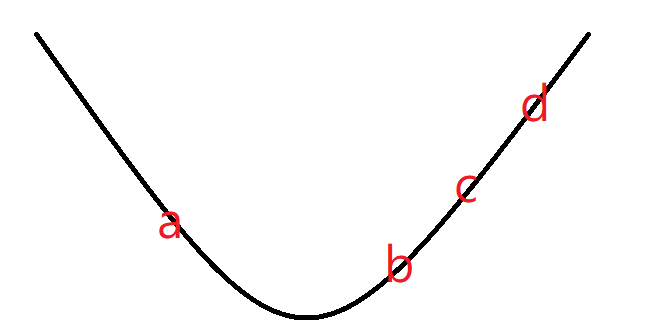
三分搜尋法

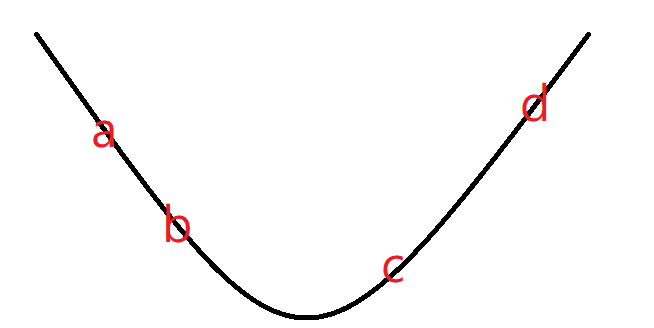
三分搜尋法

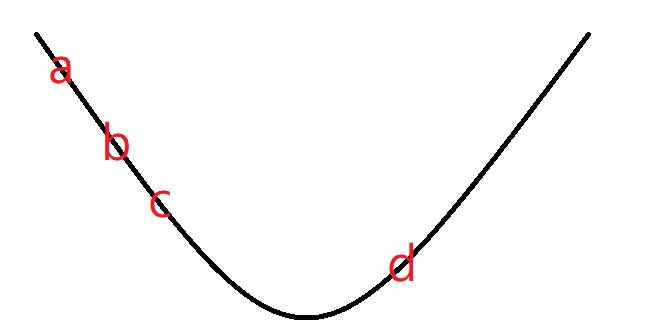
離散化

離散化

在一些題目中，數字的大小並不重要
重要的是他們之間的大小關係
離散化是將一個陣列內的數值轉換成他的名次
進而縮小值域


 

排序後二分搜

有人哪個部分有問題嗎><

Copy of deck

By tunchin kao

Source: polarischiba

Copy of deck

  • 58

More from tunchin kao