P, NP, NP-Complete, NP-Hard
何謂難題?
- 在解題的時候用電腦計算往往能大幅增加效率
- 但有些題目就算用電腦計算也需要花非常久的時間
- Ex: n-puzzle

Decision problem
- 這一類型的問題只會有yes/no兩種答案
- Ex:
- 給一個數字陣列,某個數字是否在裡面
- 給兩個數字x與y,x是否可以整除y
- 給一個數字,判斷他是不是質數
Alan Mathison Turing

- 計算機科學與人工智慧之父
- 於1936年提出Turing Machine
deterministic finite automaton
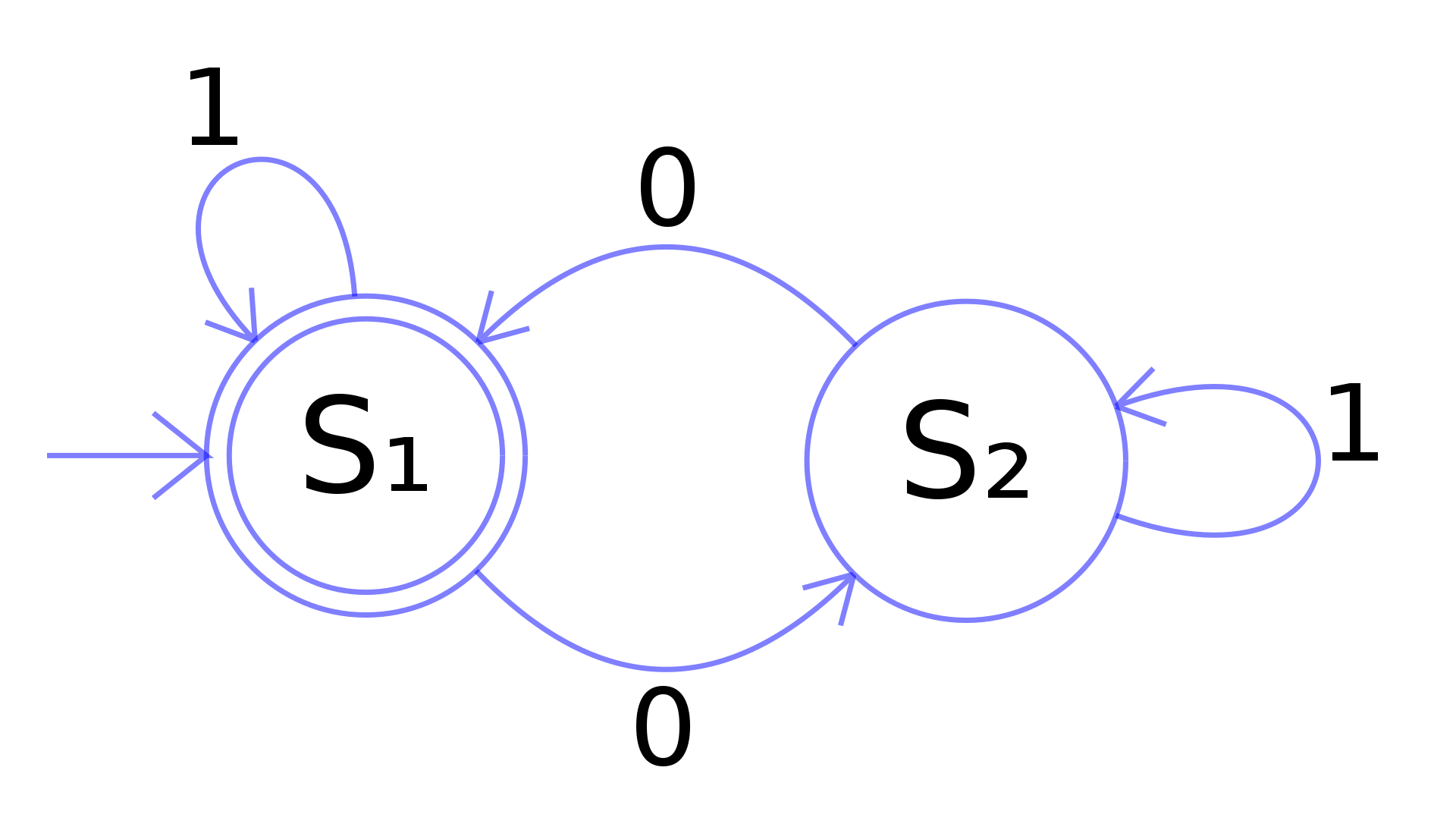
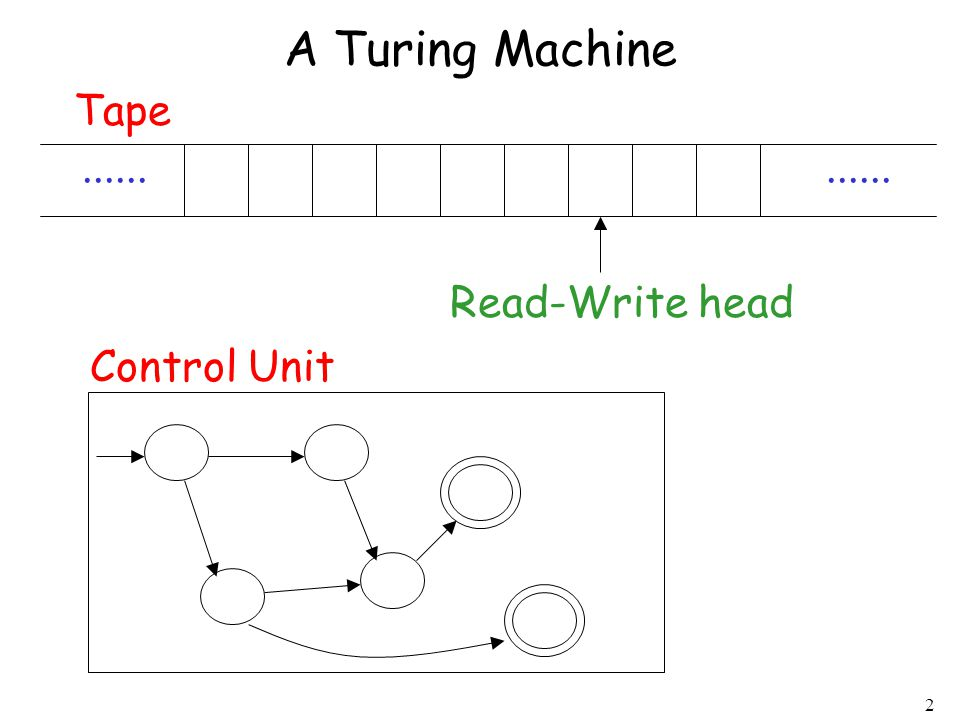
可以解決世界上所有可計算的問題
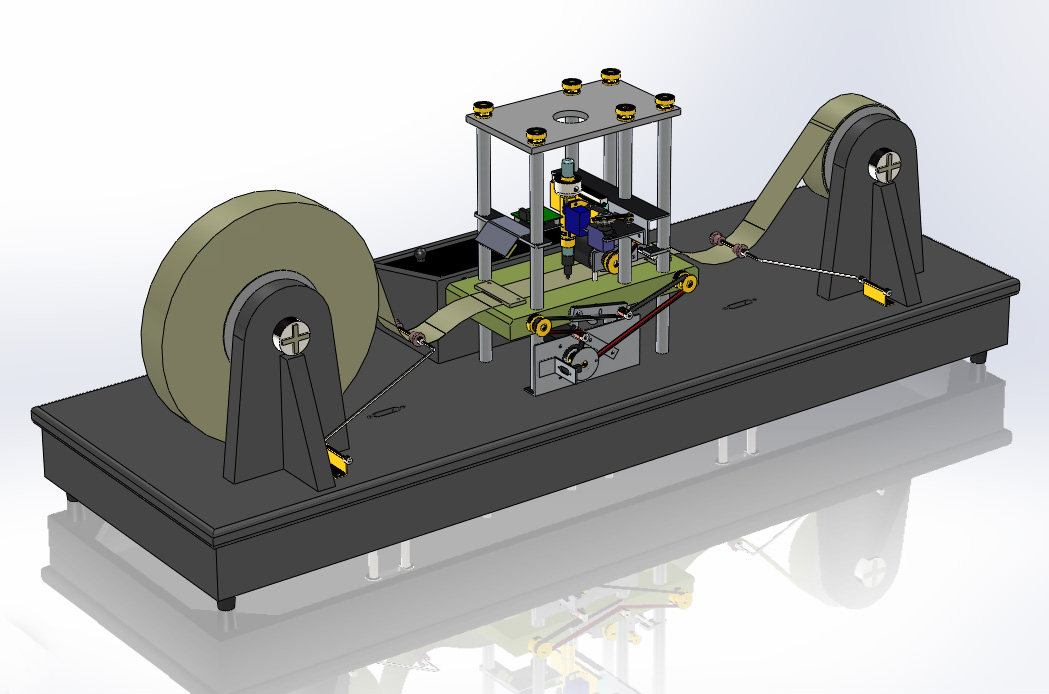
P 問題
- 滿足以下條件的問題
- 是Decision problem
- 可以被Turing Machine在Polynomial time解出來
O(N^{100}+99999999N+N \log N)
O(2^{N})
Not Polynomial time
Nondeterministic Turing machine
- 未來正規語言課程會有更詳細的解釋
- 可以先把他想成可以無限平行化的Turing machine
NP 問題
-
滿足以下條件的問題
- 是Decision problem
- 可以被Nondeterministic Turing Machine在Polynomial time解出來
- 注意NP的N不是Not的意思
- Ex:
- 給一顆亂掉魔術方塊,問有沒有方法能把他轉回來
- n-puzzle
- 倒水問題
NP 問題
-
另一種等價定義方式
- 是Decision problem
- 該問題的一組解可以可以被Turing Machine在Polynomial time驗證是否正確
-
Ex:
- 給一張地圖,是否存在一條路徑能走過圖上所有城市
- 給一條路徑,判斷他是否走過圖上所有城市
Reduction(歸約)
問題A的input
問題B的input
問題B的output
用問題B的演算法解
Polynomial time轉換
問題A的output
Polynomial time轉換
A \le_p B
NP-hard
- 比NP還要難的問題
- 如果所有NP問題都可以在Polynomial time歸約到某個問題,則稱該問題為NP-hard
- Ex:
- 給一張地圖,請你找出一條最短且可以走過圖上所有城市的路徑
NP-complete
- 一個問題,同時是NP-hard也是NP
- Ex:
- SAT問題(第一個被發現是NP-complete)
- 給一堆數字,問你能不能從中選擇一些數字是其加起來等於0
- 給一張地圖,問你能不能找到一條路徑或是回路可以走過圖上所有的城市
- 背包問題
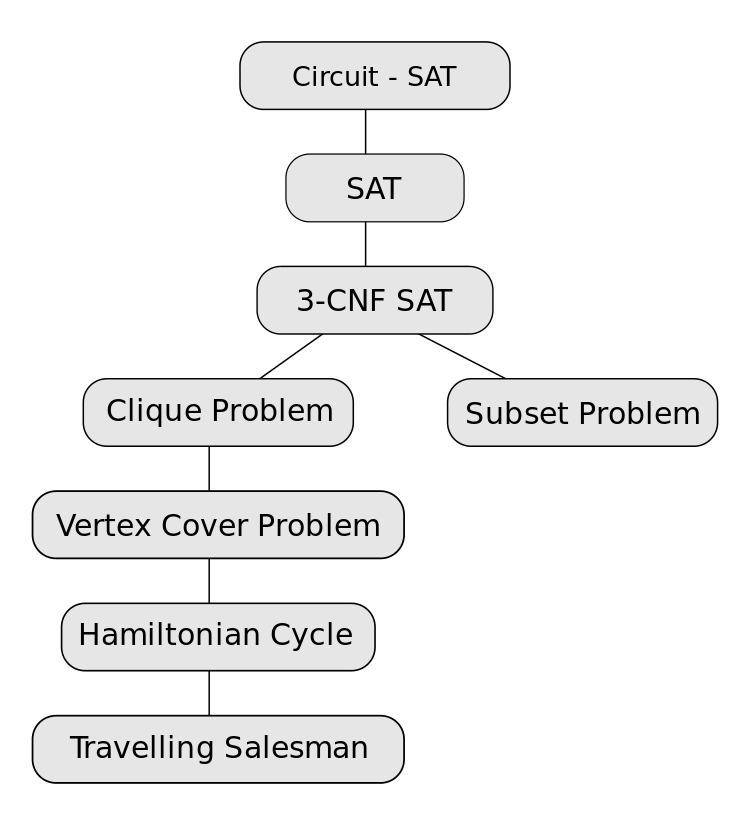
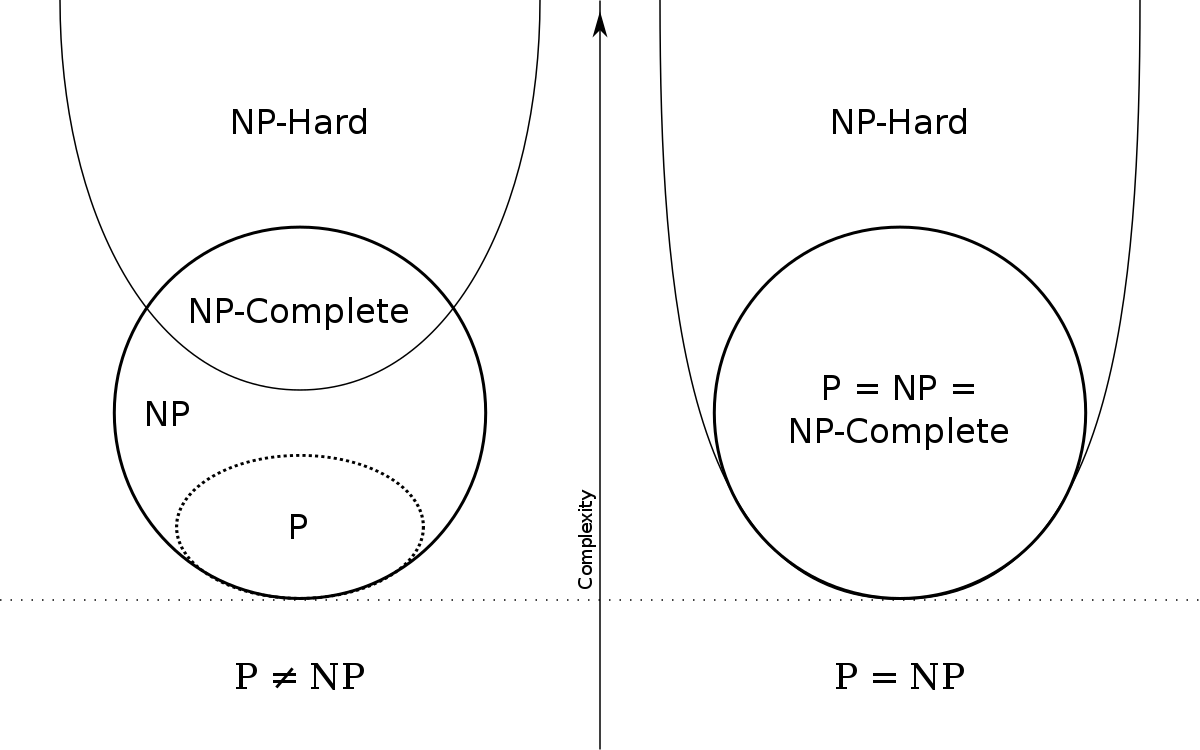
P = NP?
解出來可以拿圖靈獎+100w美金
停機問題(halting problem)
- 給一台圖靈機T和他的Input P
- 請判斷這台圖靈機會不會進入無限迴圈
構造反例
bool H(T, P); //如果會停機就return true
bool GG(P){
if ( H(P,P)==false ){
return 0;
}
while(true);
}
H(GG, GG); //會發生什麼事呢?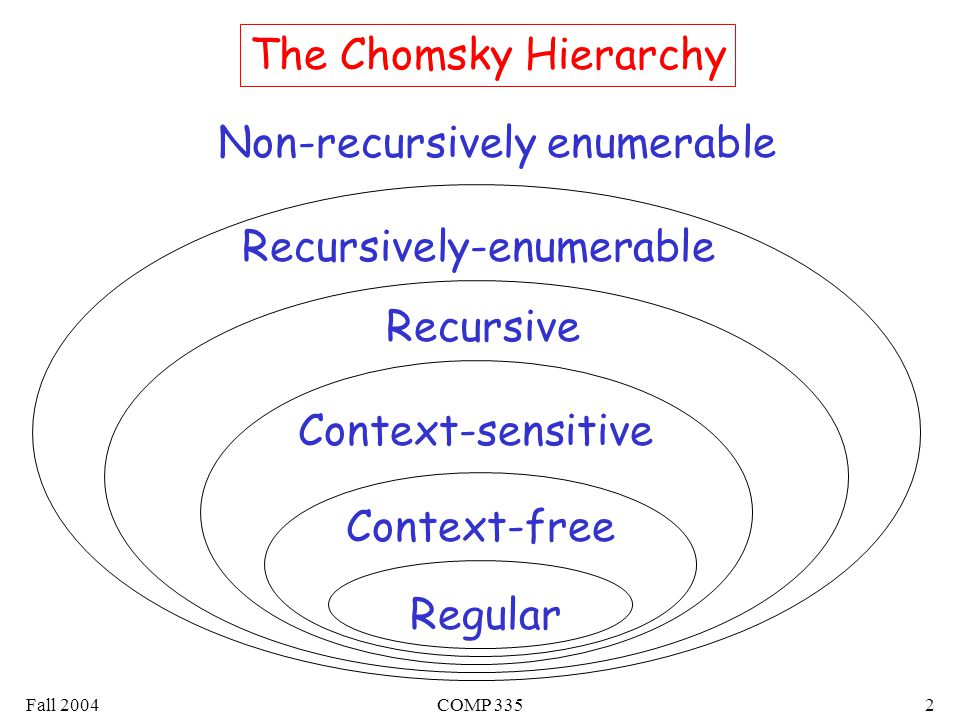
Copy of NP
By tunchin kao
Copy of NP
Dec 21th, 2019
- 81



