Álgebra


Al Juarismi (siglo IX d. C.), considerado uno de los «padres del álgebra»

Audio: https://www.jw.org/es/biblioteca/revistas/g201505/al-juarismi-padre-del-algebra/
El álgebra (del árabe: الجبر al-ŷabr ‘reintegración, recomposición’)1 es la rama de la matemática que estudia la combinación de elementos de estructuras abstractas acorde a ciertas reglas. Originalmente esos elementos podían ser interpretados como números o cantidades, por lo que el álgebra en cierto modo originalmente fue una generalización y extensión de la aritmética.23
Álgebra

La necesidad de ampliar los conocimientos aritméticos para resolver
problemas más complejos, que requerían el manejo de cantidades que,
aunque desconocidas, se manifestaban en la ocurrencia de fenómenos
naturales y sociales, que atrajeron la curiosidad de las mentes brillantes de
las generaciones pasadas.


La herramienta principal del Álgebra y en general del lenguaje matemático es la
expresión algebraica, la cual representa la relación que existe entre diferentes cantidades
y/o magnitudes utilizando los signos de operación, relación y agrupación.
Al igual que el
lenguaje común, el lenguaje matemático está constituido por símbolos que representan
ideas o conceptos.




EXAMEN DE DIAGNÓSTICO



solo para multiplicación y división

n
_____
d




7a+3a= 10a
7a+3a² =

2xy²

-5x-6y+3z

Ejercicios



Ejemplo 1
Convierte el siguiente enunciado en una expresión algebraica.

La suma del triple de un número más el doble de otro número distinto al cuadrado.
Ejemplo 1
La suma del triple de un número más el doble de otro número distinto al cuadrado.
Ejemplo 1
Procedimiento: Empezaremos a analizar y construir la expresión por partes, tomando los
diferentes elementos del enunciado.
La suma del triple de un número más el doble de otro número distinto al cuadrado.
Ejemplo 1
Procedimiento: Empezaremos a analizar y construir la expresión por partes, tomando los
diferentes elementos del enunciado.
La suma del triple de un número más el doble de otro número distinto al cuadrado.
Ejemplo 1






Ejercicios



Ejemplo 2

Ejemplo 2
Para realizar este procedimiento iniciaremos
desde “afuera”, es decir desde la
operación que describe o afecta a todos los elementos de la expresión (cuadrado), después
continuaremos con la descripción de lo que se encuentra dentro del paréntesis (resta) y por
último describiremos de izquierda a derecha los elementos que se restan.

Ejemplo 2


Ejemplo 2
El cuadrado de la diferencia del doble de un número y el cubo de otro número distinto.
El cuadrado de la resta del doble de un número y el cubo de otro número distinto.
El cuadrado de la diferencia del doble de un número y el cubo de otro.
1. José tiene un terreno cuadrado. ¿Cuál es la expresión algebraica de su
perímetro?

L+L+L+L = 4L
L*L= L²

?
2. María fue al mercado a comprar cebolla y tomate. ¿Cuántos kilos de verdura
cargó de regreso a su casa?

x + y
Si el enunciado informara adicionalmente que María compró el doble de cebolla que de
tomate entonces
2x + y
Si el enunciado informara adicionalmente que María compró el doble de cebolla que de
tomate entonces
2x + x
Siempre que intentemos resolver un problema algebraico debemos utilizar el menos
número de literales o incógnitas.
3x
3. Juan descargó tres archivos de la red de internet, cada uno el doble de pesado que el anterior.
¿Cuántos MB de datos de memoria ocupó en su
USB?

X+Y+Z
Y=2X y que Z=2Y=4x
X+2X+4X=7X

Ejercicios
El profesor Rigoberto tiene cuatro hijos. Cada uno es un año mayor que el anterior.

establece la expresión algebraica que represente las
siguientes situaciones.


Polinomios





Suma de polinomios








Ejercicios



Resta de polinomios






10-8=
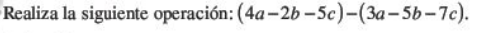


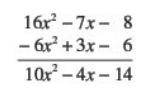
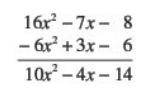


Ejercicios


Ejercicios

Multiplicación







SVM = signo de valor mayor

















Actividad







Ejercicios









Ejemplo


Ejemplo





polinomio entre polinomio



Álgebra
By Tuxtla Nauta
Álgebra
- 768



