Fractals
Weird Dimensions
and
Procedural Landspaces
NAME: IShan Bhanuka
ID: 2016A7ps0075p
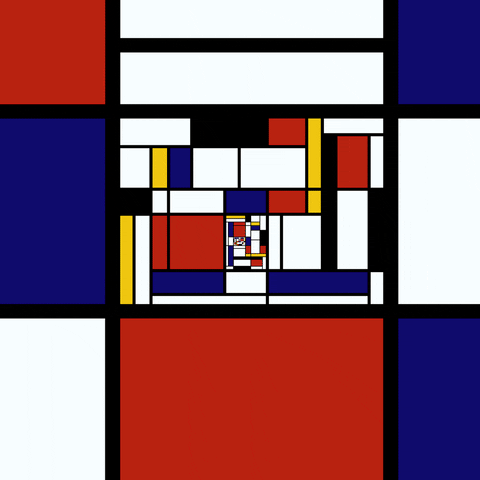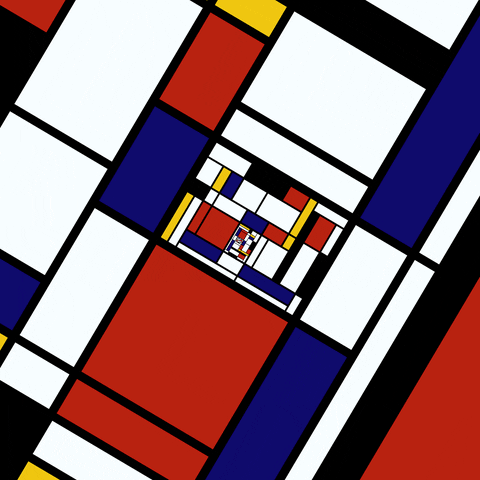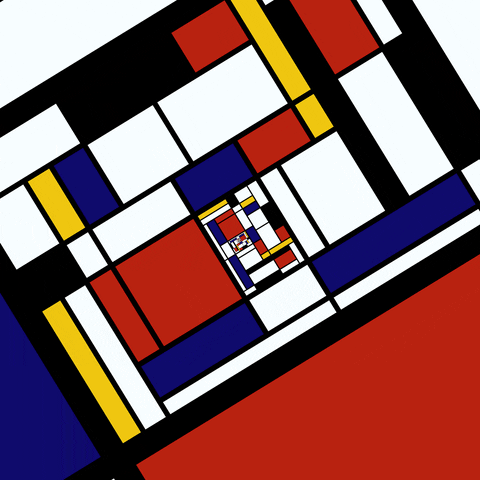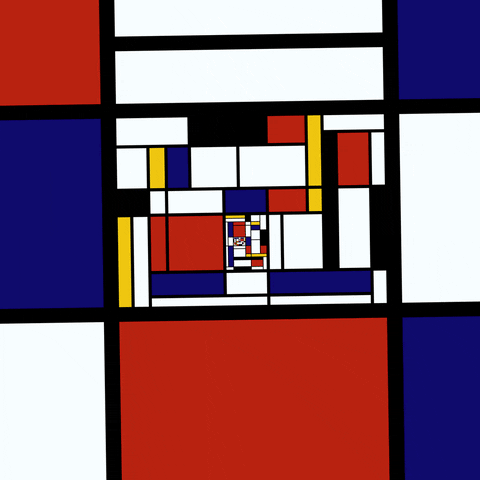
Sierpinski Gasket
Generated using fractal trees

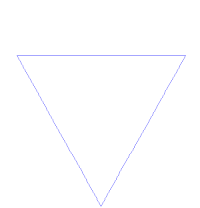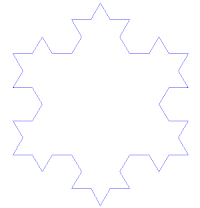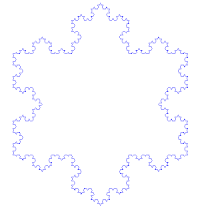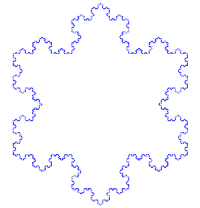
Koch snowflake
Made up of equilateral triangles
ELEGANT FRACTALS
BUT WHAT ARE THEY?
-
selF SIMILAR SHAPES
-
recursive structures
-
shapes with non-integral dimension?!
-
all of the above!!
SAME STRUCTURE RE-APPEARS at different scales
MATHEMATICALLY, "some" quantity remains unchanged when changing scale
dynamic\ quantity = f(x, t) \\
x / {t^z} = c

Zooming in on a Kock curve
-SIMILAR
SELF-
RECURSIVE STRUCTURE
var angle = 0;
var slider;
function setup() {
createCanvas(400, 400);
slider = createSlider(0, TWO_PI, PI / 4, 0.01);
}
function draw() {
background(51);
angle = slider.value();
stroke(255);
translate(200, height);
branch(100);
}
function branch(len) {
line(0, 0, 0, -len);
translate(0, -len);
if (len > 4) {
push();
rotate(angle);
branch(len * 0.67); // left branch
pop();
push();
rotate(-angle);
branch(len * 0.67); // right branch
pop();
}
}

The SUB-STRUCTURE Can be recursive generated. In the fractal tree, each branch is a fractal tree itself
LET's UNDERSTAND DIMENSION AGAIn
NON-INTEGER DIMenSION?!
LENGTH = 1
MASS = 1
SCALE = 1
LENGTH CHANGES WITH SCALE
MASS CHANGES WITH SCALE BUT WHAT IS THE AMOUNT OF CHANGE?
LENGTH = \(1/2\)
MASS = \(1/2\)
SCALE = 2
LENGTH = 1 MASS = 1
SCALE =1
LENGTH = \(1/2\) MASS = \(1/4\)
SCALE = 2




LENGTH = 1
MASS = 1
SCALe = 1
LENGTH = \(1/2\)
MASS = \(1/3\) ??
SCALe = \(1/2\)

\(SCALE * LENGTH = SCALE ^ 1 * MASS\)
\(SCALE * LENGTH = SCALE ^ {1.58} * MASS\)
\(SCALE * LENGTH = SCALE ^ 2 * MASS\)
fORMULA
\(SCALE * LENGTH = SCALE ^ {z} * MASS\)
WHERE Z IS THE DIMENSION OF THE SHAPE
FRACTALS FOR LANDSCAPE GENERATION
\(X_{N+1} = f(X_N)\)
\(X_{N+2} = f(X_{N+1})\)
THE LANDSCAPE CAN BE RECURSIVELY DIVIDED BY PROCESSING ITSELF
ADD COMPLEXITY BY SUMMING TOGETHER DIFFERENT LAYERS
FILTER OUT OUTLIERS FOR A NATURAL TRANSITION
THANK YOU
Fractals - Weird dimensions and Procedural Landscapes
By Ishan Bhanuka
Fractals - Weird dimensions and Procedural Landscapes
Presentation for Computer Graphics course assignment
- 164


