Update
Introductory Game Theory
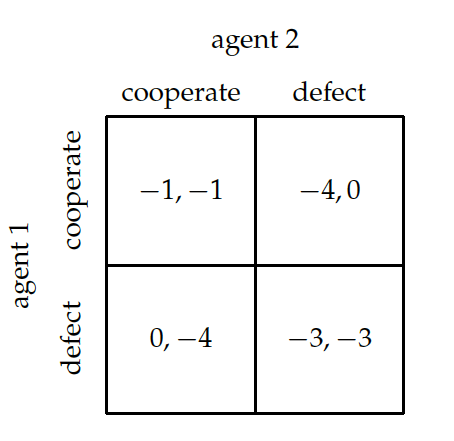
Prisoner's Dilemma
u_{1}(\sigma) \geq \max _{\sigma_{1}^{\prime} \in \Sigma_{1}} u_{1}\left(\sigma_{1}^{\prime}, \sigma_{2}\right) \quad u_{2}(\sigma) \geq \max _{\sigma_{2}^{\prime} \in \Sigma_{2}} u_{2}\left(\sigma_{1}, \sigma_{2}^{\prime}\right)
Nash Equilibrium
Start Simple
Rock Paper Scissors

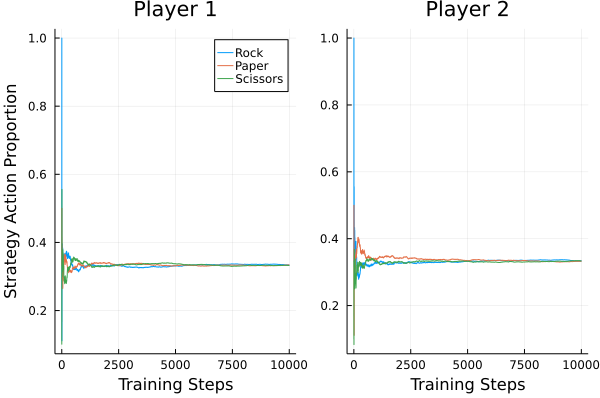
Regret Matching
Finding Nash Equilibria via Self-Play
R_{i}^{T}=\frac{1}{T} \max _{\sigma_{i}^{*} \in \Sigma_{i}} \sum_{t=1}^{T}\left(u_{i}\left(\sigma_{i}^{*}, \sigma_{-i}^{t}\right)-u_{i}\left(\sigma^{t}\right)\right)
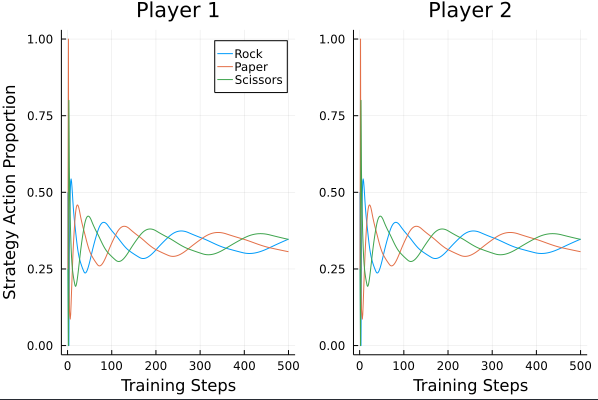
Counterfactual Regret Minimization
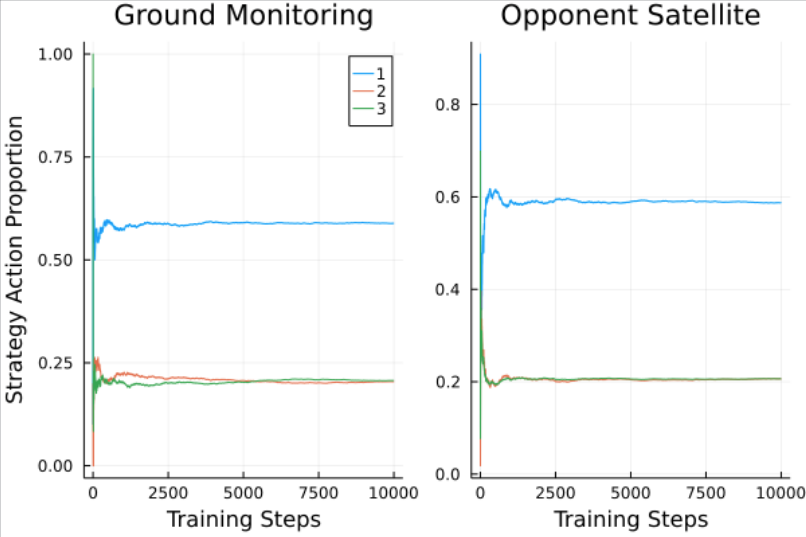
Finding Nash Equilibria via Self-Play

1
2
3
| (1,-1) | (-1,1) | (-1,1) |
|---|---|---|
| (-1,1) | (1,-1) | (-1,1) |
| (-1,1) | (-1,1) | (1,-1) |
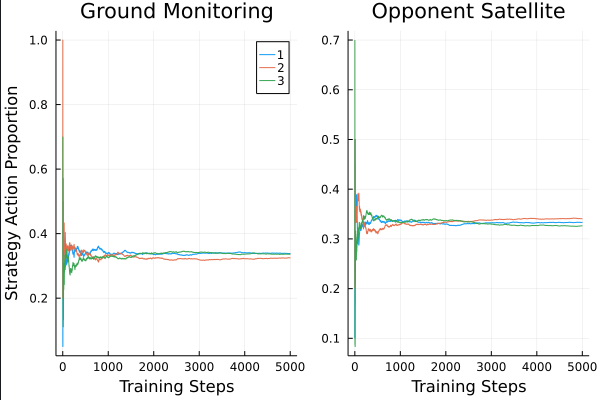
| (1,-1) | (-1,1) | (-1,1) |
|---|---|---|
| (-10,10) | (1,-1) | (-1,1) |
| (-1,1) | (-1,1) | (1,-1) |
Future Work
- Better sensing models
- More complex orbits
- [Imperfect Information] extensive-form games
- UKF tracking - detecting satellite maneuvers
- Operating over state belief
- Satellite v. Satellite
- Incorporating maneuvering actions & information gathering actions
- Exploring different methods
- CFR (poker)
- Regret Matching
- iLQGames
deck
By Tyler Becker
deck
- 424



