Levels of Parallelism
Performance Engineering in Julia 101
Introduction
- The Julia Compiler
- Processor architecture
- Benchmarking
- Levels of Parallelism
- Instruction Level Parallelism
- Vector Instructions
- Threading (shared-memory)
- Distributed
- Accelerators e.g. GPGPU
Levels of Parallelism
A (very short) introduction to the Julia compiler
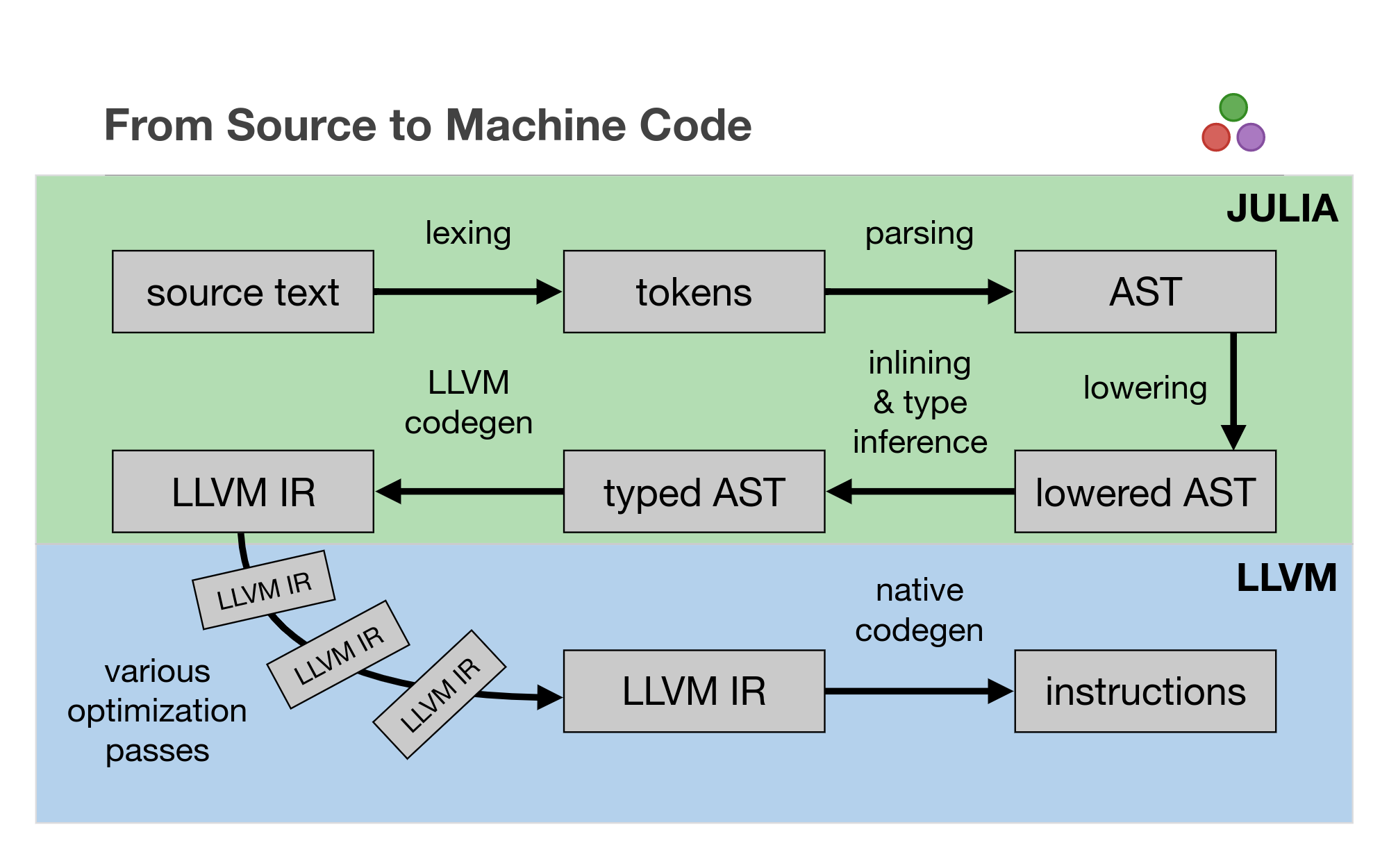
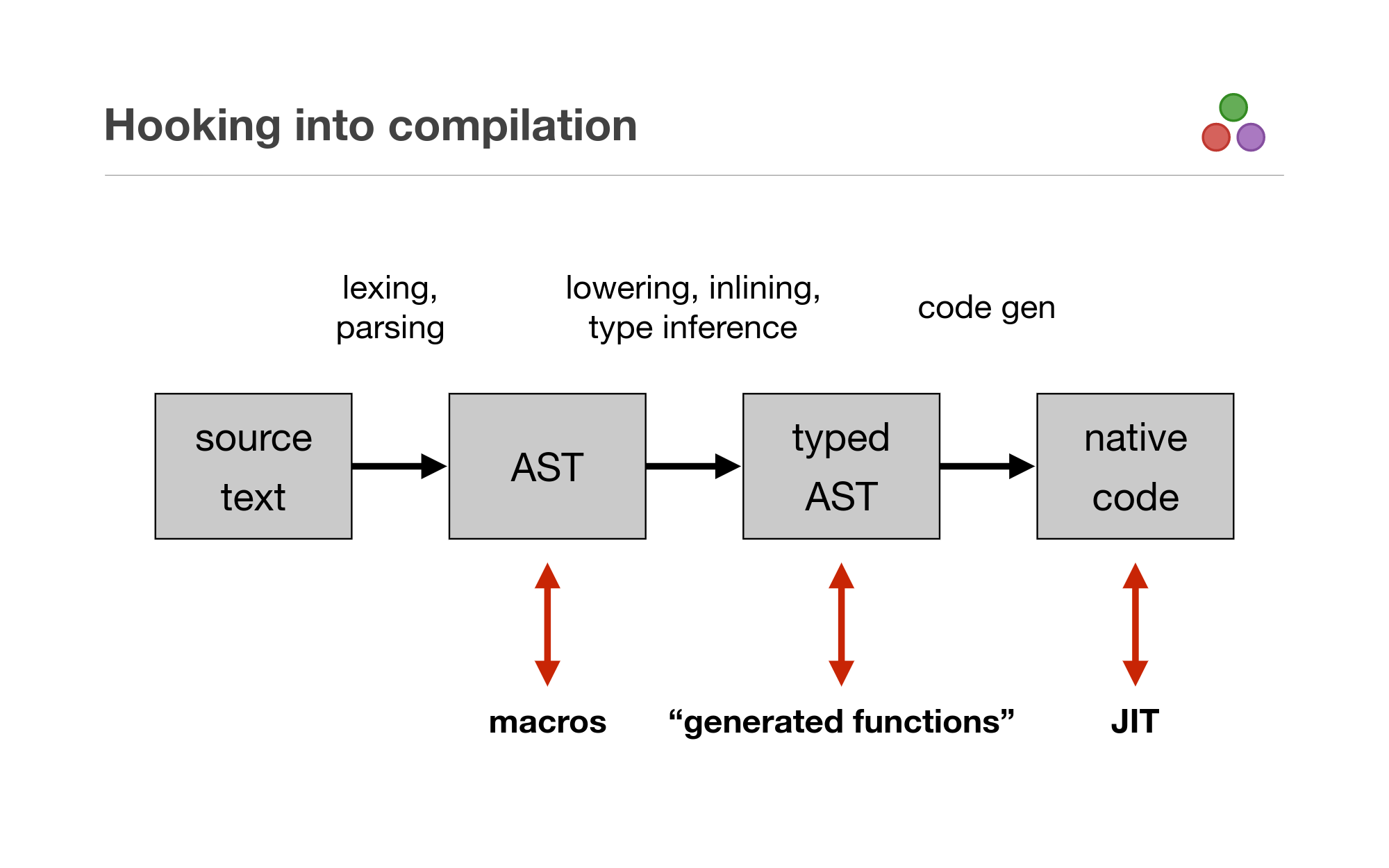
Compiler introspection in Julia
function mysum(A)
acc = zero(eltype(A))
for a in A
acc += a
end
acc
end- @code_lowered
- @code_typed & @code_warntype
- @code_llvm
- @code_native
Let's stop treating our tools like blackboxes.
julia> @code_lowered mysum(ones(1))
CodeInfo(:(begin
nothing
acc = (Main.zero)((Main.eltype)(A))
#= line 3 =#
SSAValue(0) = A
#temp# = (Base.start)(SSAValue(0))
6:
unless !((Base.done)(SSAValue(0), #temp#)) goto 15
SSAValue(1) = (Base.next)(SSAValue(0), #temp#)
a = (Core.getfield)(SSAValue(1), 1)
#temp# = (Core.getfield)(SSAValue(1), 2)
#= line 4 =#
acc = acc + a
13:
goto 6
15:
#= line 6 =#
return acc
end))@code_lowered
julia> @code_typed mysum(ones(1))
CodeInfo(:(begin
acc = (Base.sitofp)(Float64, 0)::Float64
#= line 3 =#
#temp# = 1
4:
unless (Base.not_int)(
(#temp# === (Base.add_int)((Base.arraylen)(A)::Int64, 1)::Int64)::Bool
)::Bool goto 14
SSAValue(2) = (Base.arrayref)(true, A, #temp#)::Float64
SSAValue(3) = (Base.add_int)(#temp#, 1)::Int64
a = SSAValue(2)
#temp# = SSAValue(3)
#= line 4 =#
acc = (Base.add_float)(acc, a)::Float64
12:
goto 4
14:
#= line 6 =#
return acc
end)) => Float64
@code_typed
julia> @code_warntype mysum_unstable(ones(1))
Variables:
A::Array{Float64,1}
acc::Union{Float64, Int64}
#temp#@_4::Int64
a::Float64
#temp#@_6::Float64
Body:
begin
acc::Union{Float64, Int64} = 0
#= line 3 =#
#temp#@_4::Int64 = 1
4:
unless (Base.not_int)((#temp#@_4::Int64 === (Base.add_int)((Base.arraylen)(A::Array{Float64,1})::Int64, 1)::Int64)::Bool)::Bool goto 26
SSAValue(3) = (Base.arrayref)(true, A::Array{Float64,1}, #temp#@_4::Int64)::Float64
SSAValue(4) = (Base.add_int)(#temp#@_4::Int64, 1)::Int64
a::Float64 = SSAValue(3)
#temp#@_4::Int64 = SSAValue(4)
#= line 4 =#
unless (acc::Union{Float64, Int64} isa Float64)::Bool goto 14
#temp#@_6::Float64 = $(Expr(:invoke, MethodInstance for +(::Float64, ::Float64), :(Main.+), :(acc), :(a)))::Float64
goto 22
14:
unless (acc::Union{Float64, Int64} isa Int64)::Bool goto 18
#temp#@_6::Float64 = $(Expr(:invoke, MethodInstance for +(::Int64, ::Float64), :(Main.+), :(acc), :(a)))::Float64
goto 22
18:
goto 20
20:
(Base.error)("fatal error in type inference (type bound)")::Any
22:
acc::Union{Float64, Int64} = #temp#@_6::Float64
24:
goto 4
26:
#= line 6 =#
return acc::Union{Float64, Int64}
end::Union{Float64, Int64}
@code_warntype
julia> @code_llvm mysum(ones(1))
; Function mysum
; Location: REPL[52]:2
define double @julia_mysum_64348(%jl_value_t addrspace(10)* nonnull dereferenceable(40)) {
top:
; Location: REPL[52]:3
%1 = addrspacecast %jl_value_t addrspace(10)* %0 to %jl_value_t addrspace(11)*
%2 = bitcast %jl_value_t addrspace(11)* %1 to %jl_array_t addrspace(11)*
%3 = getelementptr inbounds %jl_array_t, %jl_array_t addrspace(11)* %2, i64 0, i32 1
%4 = load i64, i64 addrspace(11)* %3, align 8
%5 = icmp eq i64 %4, 0
br i1 %5, label %L14, label %if.lr.ph
if.lr.ph: ; preds = %top
%6 = bitcast %jl_value_t addrspace(11)* %1 to double* addrspace(11)*
br label %if
if: ; preds = %if.lr.ph, %idxend
%"#temp#.04" = phi i64 [ 1, %if.lr.ph ], [ %14, %idxend ]
%acc.03 = phi double [ 0.000000e+00, %if.lr.ph ], [ %15, %idxend ]
%7 = add i64 %"#temp#.04", -1
%8 = icmp ult i64 %7, %4
br i1 %8, label %idxend, label %oob
L14.loopexit: ; preds = %idxend
; Location: REPL[52]:6
br label %L14
L14: ; preds = %L14.loopexit, %top
%acc.0.lcssa = phi double [ 0.000000e+00, %top ], [ %15, %L14.loopexit ]
ret double %acc.0.lcssa
oob: ; preds = %if
; Location: REPL[52]:3
%9 = alloca i64, align 8
store i64 %"#temp#.04", i64* %9, align 8
%10 = addrspacecast %jl_value_t addrspace(10)* %0 to %jl_value_t addrspace(12)*
call void @jl_bounds_error_ints(%jl_value_t addrspace(12)* %10, i64* nonnull %9, i64 1)
unreachable
idxend: ; preds = %if
%11 = load double*, double* addrspace(11)* %6, align 8
%12 = getelementptr double, double* %11, i64 %7
%13 = load double, double* %12, align 8
%14 = add i64 %"#temp#.04", 1
; Location: REPL[52]:4
%15 = fadd double %acc.03, %13
; Location: REPL[52]:3
%16 = icmp eq i64 %"#temp#.04", %4
br i1 %16, label %L14.loopexit, label %if
}
@code_llvm
julia> @code_native mysum(ones(1))
.text
; Function mysum {
; Location: REPL[52]:2
movq 8(%rdi), %rcx
vxorpd %xmm0, %xmm0, %xmm0
testq %rcx, %rcx
je L54
vxorpd %xmm0, %xmm0, %xmm0
xorl %eax, %eax
nopw %cs:(%rax,%rax)
L32:
cmpq %rcx, %rax
jae L55
movq (%rdi), %rdx
; Location: REPL[52]:4
vaddsd (%rdx,%rax,8), %xmm0, %xmm0
; Location: REPL[52]:3
addq $1, %rax
cmpq %rax, %rcx
jne L32
; Location: REPL[52]:6
L54:
retq
L55:
pushq %rbp
movq %rsp, %rbp
; Location: REPL[52]:3
movq %rsp, %rcx
leaq -16(%rcx), %rsi
movq %rsi, %rsp
addq $1, %rax
movq %rax, -16(%rcx)
movabsq $jl_bounds_error_ints, %rax
movl $1, %edx
callq *%rax
nop
;}
@code_native
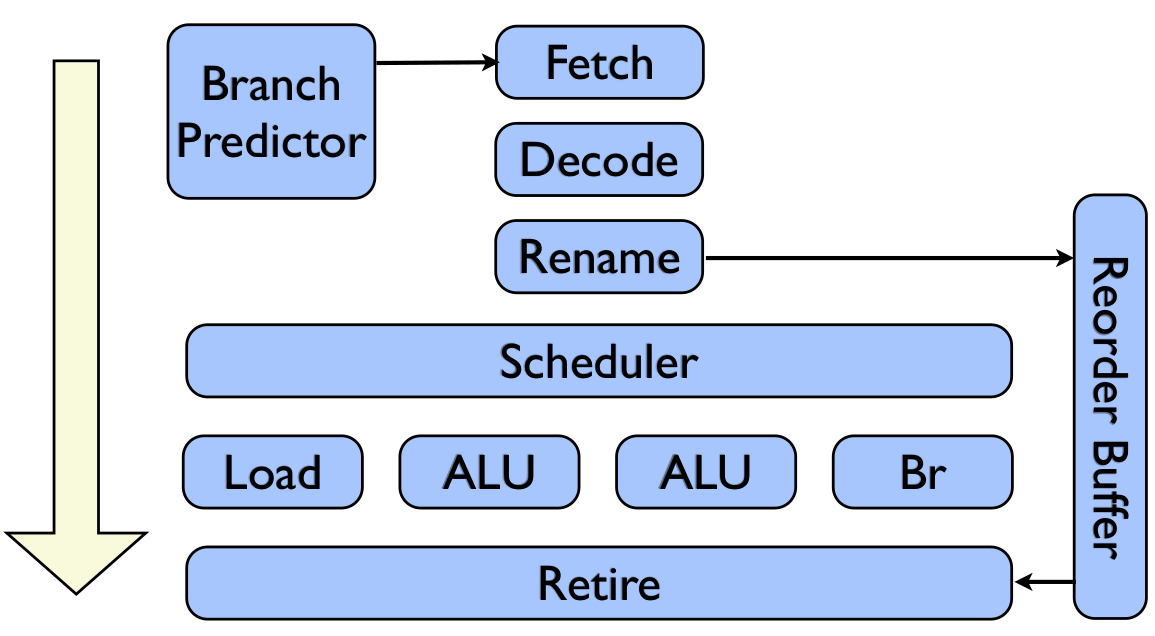
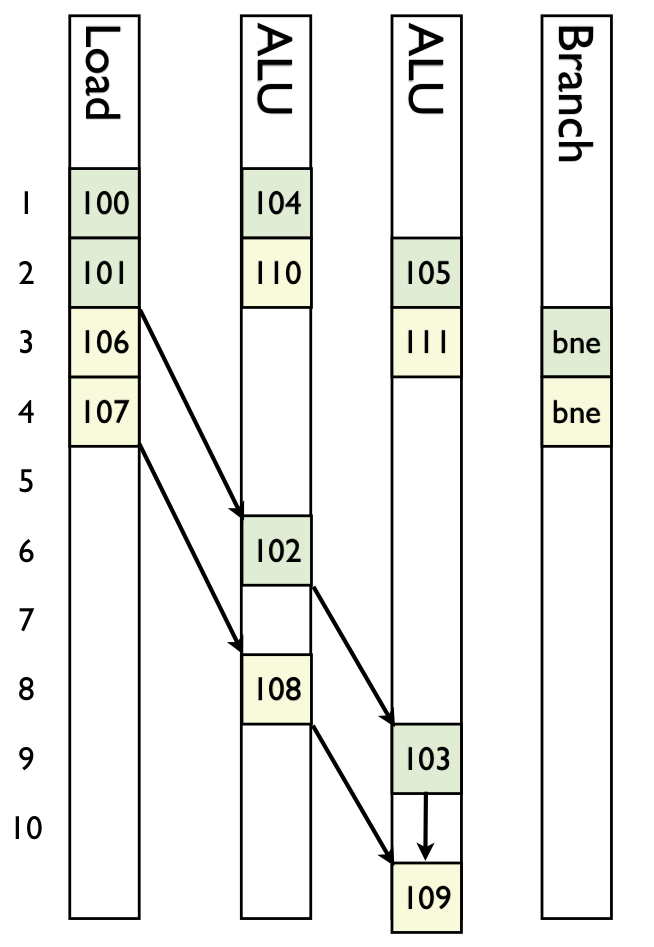
What has your processor done for you recently
As programmers we have the mental model that a processor takes your instructions in linear order
Processors are:
- Out-of-order
- Superscalar
- Predictive
- Micro-ops
An (idealized) processor
http://llvm.org/devmtg/2013-04/olesen-slides.pdf
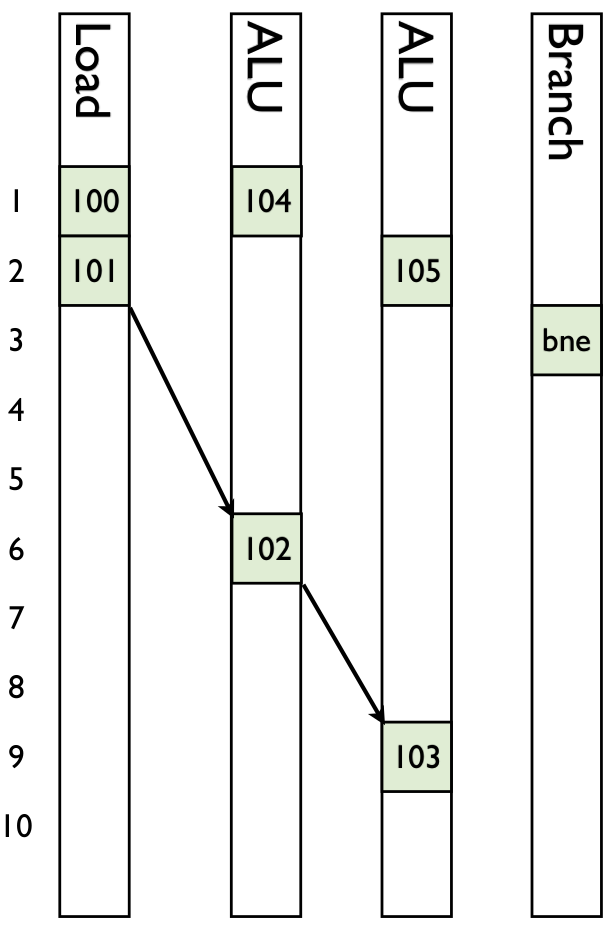
Dot product
http://llvm.org/devmtg/2013-04/olesen-slides.pdf
function dot(a::AbstractVector{T}, b::AbstractVector{T}) where T
@assert size(a) == size(b)
acc = zero(T)
@inbounds for i in eachindex(a, b)
acc += a[i] * b[i]
end
return acc
endL32:
movsd (%rcx), %xmm1 # xmm1 = mem[0],zero
mulsd (%rdx), %xmm1
addsd %xmm1, %xmm0
Source line: 3
addq $8, %rdx
addq $8, %rcx
decq %rax
jne L32
Dot product
http://llvm.org/devmtg/2013-04/olesen-slides.pdf

http://llvm.org/devmtg/2013-04/olesen-slides.pdf

http://llvm.org/devmtg/2013-04/olesen-slides.pdf


http://llvm.org/devmtg/2013-04/olesen-slides.pdf

http://llvm.org/devmtg/2013-04/olesen-slides.pdf

Lot more topics to talk about,
let me know if you are interested!
Benchmarking Methodology
- Measure first! Don't try to guess the performance of your code.
- If you don't measure, you can't improve.
- Computers are noisy! Many people use lowest runtime.
- Read the performance tips in the Julia manual.
- Don't benchmark in global scope.
- Global variables are performance pitfalls.
Benchmarking
Steps
- Check for type-instabilities with @code_warntype
- Benchmark using @btime and @benchmark from BenchmarkTools.jl
- Use Julia profiler and ProfileView.jl
- Use the memory allocation tracker
About Global Scope
A global variable might have its value, and therefore its type, change at any given point. This makes it difficult/nigh impossible for the compiler to reason about/optimize code using global variables.
Julia uses functions as its compilation unit and any code that is performance critical or being benchmarked should be inside a function.
Using BenchmarksTools.jl
julia> using BenchmarkTools
julia> @benchmark sin(1)
BenchmarkTools.Trial:
memory estimate: 0 bytes
allocs estimate: 0
--------------
minimum time: 7.677 ns (0.00% GC)
median time: 8.223 ns (0.00% GC)
mean time: 10.223 ns (0.00% GC)
maximum time: 129.435 ns (0.00% GC)
--------------
samples: 10000
evals/sample: 999julia> @benchmark sum($(rand(1000)))
BenchmarkTools.Trial:
memory estimate: 0 bytes
allocs estimate: 0
--------------
minimum time: 69.184 ns (0.00% GC)
median time: 79.951 ns (0.00% GC)
mean time: 88.368 ns (0.00% GC)
maximum time: 211.363 ns (0.00% GC)
--------------
samples: 10000
evals/sample: 974
julia> @benchmark sum(rand(1000))
BenchmarkTools.Trial:
memory estimate: 7.94 KiB
allocs estimate: 1
--------------
minimum time: 1.115 μs (0.00% GC)
median time: 1.472 μs (0.00% GC)
mean time: 2.177 μs (18.77% GC)
maximum time: 326.092 μs (97.69% GC)
--------------
samples: 10000
evals/sample: 10
Always interpolate inputs into your benchmark to measure the part of your code that you are interested in.
Timing distributions
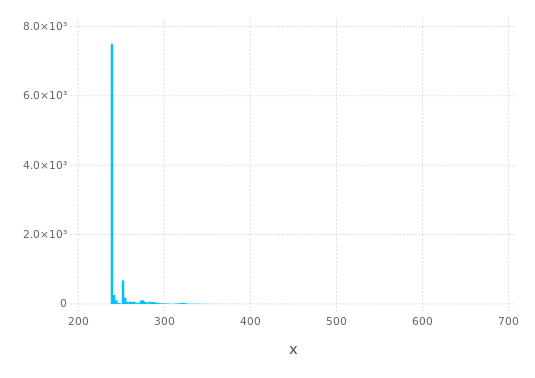
Using the Profiler
@profile fun() # Profile a specific function
Profile.clear() # Clear the recorded profile
Profile.print() # Print the recorded profile
Profile.print(C=true) # Print the profile including calls into C
# The textual output of the profiler can be hard to understand
# ProfileView.jl gives you a graphical representation
using ProfileView
ProfileView.view()# To track memory allocations you have to start Julia
# with the memory allocation tracker enabled.
# Track only allocation in user code
julia --track-allocation=user
# Track allocation in all code
julia --track-allocation=all
# After quitting Julia *.mem files are created that
# contain cumulative amounts of allocated memory.
# Since we are tracking all allocations, we will gather
# a lot of noisy data. To cut down the noise run your
# code once and then use Profiler.clear_malloc_data() to
# reset the allocation counts and then run your code again
# the output will only contain relevant data.Gaining additional insights
- https://github.com/cstjean/FProfile.jl
- https://github.com/cstjean/TraceCalls.jl
- Learn about Linux `perf`
Advanced profiling tools
Code Analyzer
- https://github.com/vchuravy/IACA.jl
SIMD Vectorization
# LLVM IR uses <2 x f64> to denote vector operationsSIMD Vectorization
function add(out, x, y)
for i in 1:length(out)
out[i] = x[i] + y[i]
end
endEach loop iteration is independent
Does this vectorize?
code_llvm(add, (Vector{Float64}, Vector{Float64}, Vector{Float64}))function add(out, x, y)
@inbounds for i in 1:length(out)
out[i] = x[i] + y[i]
end
end@inbounds removes the bound-checks and gives LLVM the opportunity to auto-vectorize this code.
Reductions
function sum(X)
acc = zero(eltype(X))
for i in 1:length(X)
acc += X[i]
end
return acc
endQ: Does this loop vectorize? Think about if each loop iteration is independent.
Check with @code_llvm for Int64 and Float64.
function sum(X)
acc = zero(eltype(X))
@inbounds @simd for i in 1:length(X)
acc += X[i]
end
return acc
endInteger addition is associative and the order of operations has no impact.
Floating-point addition is non-associative and the order of operations is important.
Explicit SIMD with SIMD.jl
using SIMD
function add(out::Vector{Float64}, x::Vector{Float64}, y::Vector{Float64})
@assert length(x) % 4 == 0
@assert length(x) == length(y)
# My laptop supports AVX 256bit 4xFloat64
for i in 1:4:length(x)
vx = vload(Vec{4, Float64}, x, i)
vy = vload(Vec{4, Float64}, y, i)
vo = vx + vy
vstore(vo, out, i)
end
end
Idea: Create a Vector type that SIMDVector{T, N}, where getindex is a vload.
The SLP Vectorizer
function foo(a1, a2, b1, b2)
c1 = a1*(a1 + b1)/b1 + 50*b1/a1
c2 = a2*(a2 + b2)/b2 + 50*b2/a2
return (c1, c2)
end %5 = fadd double %1, %3
%6 = fmul double %5, %1
%7 = fdiv double %6, %3
%8 = fmul double %3, 5.000000e+01
%9 = fdiv double %8, %1
%10 = fadd double %9, %7
; Location: REPL[6]:3
%11 = fadd double %2, %4
%12 = fmul double %11, %2
%13 = fdiv double %12, %4
%14 = fmul double %4, 5.000000e+01
%15 = fdiv double %14, %2
%16 = fadd double %15, %13
%5 = insertelement <2 x double> undef, double %1, i32 0
%6 = insertelement <2 x double> %5, double %2, i32 1
%7 = insertelement <2 x double> undef, double %3, i32 0
%8 = insertelement <2 x double> %7, double %4, i32 1
%9 = fadd <2 x double> %6, %8
%10 = fmul <2 x double> %6, %9
%11 = fdiv <2 x double> %10, %8
%12 = fmul <2 x double> %8, <double 5.000000e+01, double 5.000000e+01>
%13 = fdiv <2 x double> %12, %6
%14 = fadd <2 x double> %13, %11
An aside: IACA.jl
Pkg.clone("https://github.com/vchuravy/IACA.jl")# Similar to code_llvm
IACA.code_llvm(func, (Type,))
# What has my compiler ever done for me
IACA.code_llvm(func, (Type,), optimize=false)
# What would my code do on a different platform
IACA.code_llvm(func, (Type,), cpu="knl")
# Switching optimization level
IACA.optlevel[] = 3
IACA.code_llvm(func, (Type,))The features below only work on Julia 0.7
struct RGBA
r :: Float64
g :: Float64
b :: Float64
a :: Float64
end
Base.rand(::Type{RGBA}) = RGBA(rand(), rand(), rand(), rand())
function myscale!(colors::AbstractVector{RGBA}, α::Float64)
for i in 1:length(colors)
c = colors[i]
r = α * c.r
g = α * c.g
b = α * c.b
a = α * c.a
colors[i] = RGBA(r, g, b, a)
end
end
IACA.code_llvm(myscale!, (typeof([rand(RGBA)]),Float64))What kinds of parallelism do you see?
struct RGBA
r :: Float64
g :: Float64
b :: Float64
a :: Float64
end
Base.rand(::Type{RGBA}) = RGBA(rand(), rand(), rand(), rand())
function myscale!(colors::AbstractVector{RGBA}, α::Float64)
@inbounds for i in 1:length(colors)
c = colors[i]
r = α * c.r
g = α * c.g
b = α * c.b
a = α * c.a
colors[i] = RGBA(r, g, b, a)
end
end
IACA.code_llvm(myscale!, (typeof([rand(RGBA)]),Float64))
IACA.optlevel[] = 3
IACA.code_llvm(myscale!, (typeof([rand(RGBA)]),Float64))struct RGBA
r :: Float64
g :: Float64
b :: Float64
a :: Float64
end
Base.rand(::Type{RGBA}) = RGBA(rand(), rand(), rand(), rand())
function myscale!(colors::AbstractVector{RGBA}, α::Float64)
@inbounds @simd for i in 1:length(colors)
c = colors[i]
r = α * c.r
g = α * c.g
b = α * c.b
a = α * c.a
colors[i] = RGBA(r, g, b, a)
end
end
IACA.optlevel[] = 2
IACA.code_llvm(myscale!, (typeof([rand(RGBA)]),Float64))maybe we are just missing @simd...
struct Vec3{T}
x::T
y::T
z::T
end
Base.rand(::Type{<:Vec3{T}}) where {T} = Vec3{T}(rand(T), rand(T), rand(T))
function sum_vec(vects::AbstractVector{Vec3{T}}) where {T}
xsum = ysum = zsum = zero(T)
for v in vects
xsum += v.x
ysum += v.y
zsum += v.z
end
Vec3{T}(xsum, ysum, zsum)
end
vects = [rand(Vec3{Float64}) for _ = 1:10000];What kinds of parallelism do you see?
function sum_vec2(vects::AbstractVector{Vec3{T}}) where {T}
xsum = ysum = zsum = zero(T)
@inbounds for v in vects
xsum += v.x
ysum += v.y
zsum += v.z
end
Vec3{T}(xsum, ysum, zsum)
end
IACA.code_llvm(sum_vec2, (typeof(vects),))function sum_vec3(vects::AbstractVector{Vec3{T}}) where {T}
xsum = ysum = zsum = zero(T)
@inbounds for v in vects
@fastmath begin
xsum += v.x
ysum += v.y
zsum += v.z
end
end
Vec3{T}(xsum, ysum, zsum)
endIACA.code_llvm(sum_vec3, (typeof(vects),))
IACA.code_llvm(sum_vec3, (typeof(vects),), cpu="knl")Can we do more?
function myscale!(colors::AbstractVector{RGBA}, α::Float64)
@inbounds for i in 1:length(colors)
c = colors[i]
r = α * c.r
g = α * c.g
b = α * c.b
a = α * c.a
colors[i] = RGBA(r, g, b, a)
end
endfunction sum_vec3(vects::AbstractVector{Vec3{T}}) where {T}
xsum = ysum = zsum = zero(T)
@inbounds for v in vects
@fastmath begin
xsum += v.x
ysum += v.y
zsum += v.z
end
end
Vec3{T}(xsum, ysum, zsum)
endStructsOfArrays.jl
soa_rgba = convert(StructOfArrays, [rand(RGBA) for _ in 1:10000])
IACA.code_llvm(myscale!, (typeof(soa_rgba), Float64))soa_vects = convert(StructOfArrays, vects)
IACA.code_llvm(sum_vec3, (typeof(soa_rgba),))Threading
Julia threading model is based on a fork-join approach and is still considered experimental.
Fork-join describes the control flow that a group of threads undergoes. Execution is forked and a anonymous function is then run across all threads.
All threads have to join together and serial execution continues.
Hardware
> lscpu
...
Thread(s) per core: 2
Core(s) per socket: 2
...
Model name: Intel(R) Core(TM) i7-7660U CPU @ 2.50GHz
...
L1d cache: 32K
L1i cache: 32K
L2 cache: 256K
L3 cache: 4096K
...
Flags: ... avx2 ...> lscpu
...
Thread(s) per core: 2
Core(s) per socket: 12
...
Model name: AMD Ryzen Threadripper 1920X 12-Core Processor
...
L1d cache: 32K
L1i cache: 64K
L2 cache: 512K
L3 cache: 8192K
...
Flags: ... avx2 ...Threading
JULIA_NUM_THREADS=4 julia
using Base.Threads
a = zeros(nthreads()*10)
@threads for i in 1:length(a)
a[i] = threadid()
endSpecial care needs to be taken if the loop body access has side-effects or accesses global state. (This includes IO and random numbers)
A = zeros(10_000)
@threads for i in 1:length(A)
A[i] = rand()
end
const rngs = [MersenneTwister(rand(UInt64)) for i in 1:nthreads()]
@threads for i in 1:length(A)
A[i] = rand(rngs[threadid()])
endAtomics
acc = 0
@threads for i in 1:10_000
global acc
acc += 1
endacc = Atomic{Int64}(0)
@threads for i in 1:10_000
atomic_add!(acc, 1)
endjulia> acc
5214
julia> acc
Base.Threads.Atomic{Int64}(10000)Locks
https://docs.julialang.org/en/latest/stdlib/parallel/#Synchronization-Primitives-1
using Base.Threads
const acc = Ref{Int64}(0)const mlock = Mutex()
function f1()
@threads for i in 1:10_000
lock(mlock)
acc[] += 1
unlock(mlock)
end
endconst splock = SpinLock()
function f2()
@threads for i in 1:10_000
lock(splock)
acc[] += 1
unlock(splock)
end
endconst rsplock = RecursiveSpinLock()
function f3()
@threads for i in 1:10_000
lock(rsplock)
acc[] += 1
unlock(rsplock)
end
end# 4 Threads (1 Thread)
julia> @btime f1()
664.202 μs # (278.338 μs)
julia> @btime f2()
183.159 μs # (60.344 μs)
julia> @btime f3()
219.427 μs # (121.051 μs)
# Using Atomics
julia> @btime g()
54.480 μs # (45.277 μs)
julia> @btime h()
3.096 μs A very useful trick
@threads for id in 1:nthreads()
#each thread does something
endjulia> data = rand(3*2^19);
If your @threads performance with one thread is not as fast as a non @threads version something is off..., but yeah for linear scaling.
function threaded_sum(arr)
@assert length(arr) % nthreads() == 0
results = zeros(eltype(arr), nthreads())
@threads for tid in 1:nthreads()
# split work
acc = zero(eltype(arr))
len = div(length(arr), nthreads())
domain = ((tid-1)*len +1):tid*len
@inbounds for i in domain
acc += arr[i]
end
results[tid] = acc
end
sum(results)
end
| NT | Skylake | AMD TR |
|---|---|---|
| sum | 514.476 μs | 430.409 μs |
| 1 | 1.578 ms | 1.206 ms |
| 2 | 831.411 μs | 575.872 μs |
| 4 | 417.656 μs | 294.724 μs |
| 6 | X | 215.986 μs |
| 12 | X | 109.536 μs |
| 24 | X | 57.197 μs |
Hmmm...
function threaded_sum(arr)
...
@inbounds for i in domain
acc += arr[i]
end
...
end
function threaded_sum2(arr)
@assert length(arr) % nthreads() == 0
results = zeros(eltype(arr), nthreads())
@threads for tid in 1:nthreads()
# split work
acc = zero(eltype(arr))
len = div(length(arr), nthreads())
domain = ((tid-1)*len +1):tid*len
@inbounds @simd for i in domain
acc += arr[i]
end
results[tid] = acc
end
sum(results)
end
Hyperthreading...
and superlinear speedup from 1-2 threads on Threadripper, due to cache effect. (Data is 12MB; 2xL3 = 16MB)
| NT | Skylake | AMD TR |
|---|---|---|
| sum | 514.476 μs | 430.409 μs |
| 1 | 493.384 μs | 401.755 μs |
| 2 | 282.030 μs | 73.408 μs |
| 4 | 230.988 μs | 37.541 μs |
| 6 | X | 29.185 μs |
| 12 | X | 16.491 μs |
| 24 | X | 17.693 μs |
Hmmm...
| NT | Skylake | AMD TR |
|---|---|---|
| sum | 4.970 ms | 3.477 ms |
| 1 | 4.996 ms | 3.249 ms |
| 2 | 3.867 ms | 2.241 ms |
| 4 | 2.742 ms | 1.195 ms |
| 6 | X | 1.143 ms |
| 12 | X | 1.225 ms |
| 24 | X | 1.305 ms |
| NT | Skylake | AMD TR |
|---|---|---|
| sum | 2.423 ms | 1.723 ms |
| 1 | 2.295 ms | 1.610 ms |
| 2 | 1.307 ms | 1.158 ms |
| 4 | 1.106 ms | 582.885 μs |
| 6 | X | 470.023 μs |
| 12 | X | 627.699 μs |
| 24 | X | 595.068 μs |
False sharing
function f()
acc = zeros(Int64, nthreads())
@threads for tid in 1:nthreads()
for i in 1:10_000
acc[tid] += 1
end
end
sum(acc)
end
function g()
CACHE_LINE = 64 #bytes
elems = div(CACHE_LINE, sizeof(Int64))
acc = zeros(Int64, nthreads()*elems)
@threads for tid in 1:nthreads()
store = (tid-1)*elems+1
for i in 1:10_000
acc[store] += 1
end
end
sum(acc)
endjulia> @benchmark f()
BenchmarkTools.Trial:
memory estimate: 144 bytes
allocs estimate: 2
--------------
minimum time: 23.625 μs (0.00% GC)
median time: 59.918 μs (0.00% GC)
mean time: 61.392 μs (0.00% GC)
maximum time: 3.349 ms (0.00% GC)
--------------
samples: 10000
evals/sample: 1
julia> @benchmark g()
BenchmarkTools.Trial:
memory estimate: 448 bytes
allocs estimate: 2
--------------
minimum time: 14.031 μs (0.00% GC)
median time: 15.098 μs (0.00% GC)
mean time: 15.686 μs (0.00% GC)
maximum time: 514.505 μs (0.00% GC)
--------------
samples: 10000
evals/sample: 1
https://software.intel.com/en-us/articles/avoiding-and-identifying-false-sharing-among-threads
using BenchmarkTools
using Base.Threads
println("Number of threads: ", nthreads())
function myfun(rng::MersenneTwister)
s = 0.0
N = 10000
for i=1:N
s+=det(randn(rng, 3,3))
end
s/N
end
rgi = [MersenneTwister(rand(UInt)) for _ in 1:nthreads()]
function bench(rgi)
a = zeros(1000)
@threads for i=1:length(a)
a[i] = myfun(rgi[threadid()])
end
end
result = @benchmark bench($rgi)
display(result)BenchmarkTools.Trial:
memory estimate: 4.32 GiB
allocs estimate: 40000002
--------------
minimum time: 4.063 s (4.03% GC)
median time: 4.217 s (3.57% GC)
mean time: 4.217 s (3.57% GC)
maximum time: 4.371 s (3.14% GC)
--------------
samples: 2
evals/sample: 1
BenchmarkTools.Trial:
memory estimate: 3.52 GiB
allocs estimate: 34212074
--------------
minimum time: 3.346 s (0.00% GC)
median time: 3.960 s (10.85% GC)
mean time: 3.960 s (10.85% GC)
maximum time: 4.574 s (18.78% GC)
--------------
samples: 2
evals/sample: 1
4 Threads
1 Thread
- Memory allocations in hot-loop
- Eliminate allocs caused by rand
- Investigate how det is implemented
- Implement det!
- Remove overhead to library call
- Use profiling tools
- Start using StaticArrays
@edit det(zeros(3, 3)) -> det(lufact(A))lufact{T<:AbstractFloat}(A::Union{AbstractMatrix{T},AbstractMatrix{Complex{T}}}, pivot::Union{Type{Val{false}},
Type{Val{true}}} = Val{true}) = lufact!(copy(A), pivot)det!(A) = det(lufact!(A))
det!(A) = det(LinAlg.generic_lufact!(A))Full story here
Final code
using BenchmarkTools
using StaticArrays
using Base.Threads
println("Number of threads: ", nthreads())
function myfun(rng::MersenneTwister)
s = 0.0
N = 10000
for i=1:N
s += det(randn(rng, SMatrix{3, 3}))
end
s/N
end
rgi = [MersenneTwister(abs(rand(Int))) for s in 1:nthreads()]
function bench(rgi)
a = zeros(1000)
@threads for i=1:length(a)
@inbounds a[i] = myfun(rgi[threadid()])
end
end
result = @benchmark bench($rgi)
display(result)Final code
BenchmarkTools.Trial:
memory estimate: 7.98 KiB
allocs estimate: 2
--------------
minimum time: 588.229 ms (0.00% GC)
median time: 654.259 ms (0.00% GC)
mean time: 641.654 ms (0.00% GC)
maximum time: 669.961 ms (0.00% GC)
--------------
samples: 8
evals/sample: 1
BenchmarkTools.Trial:
memory estimate: 3.52 GiB
allocs estimate: 34212074
--------------
minimum time: 3.346 s (0.00% GC)
median time: 3.960 s (10.85% GC)
mean time: 3.960 s (10.85% GC)
maximum time: 4.574 s (18.78% GC)
--------------
samples: 2
evals/sample: 1
NUMA aware threading
https://software.intel.com/en-us/articles/optimizing-applications-for-numa


UMA
NUMA
NUMA aware threading

NUMA aware threading
numactl --hardware
available: 1 nodes (0)
node 0 cpus: 0 1 2 3
node 0 size: 15934 MB
node 0 free: 2410 MB
node distances:
node 0
0: 10
vchuravy@helios ~ $ numactl --hardware
available: 2 nodes (0-1)
node 0 cpus: 0 1 2 3 4 5 12 13 14 15 16 17
node 0 size: 16000 MB
node 0 free: 15394 MB
node 1 cpus: 6 7 8 9 10 11 18 19 20 21 22 23
node 1 size: 16102 MB
node 1 free: 15403 MB
node distances:
node 0 1
0: 10 16
1: 16 10
lstopo from HWLoc helps us understand this better
Machine (31GB total) + Package L#0
NUMANode L#0 (P#0 16GB)
L3 L#0 (8192KB)
L2 L#0 (512KB) + L1d L#0 (32KB) + L1i L#0 (64KB) + Core L#0
PU L#0 (P#0)
PU L#1 (P#12)
L2 L#1 (512KB) + L1d L#1 (32KB) + L1i L#1 (64KB) + Core L#1
PU L#2 (P#1)
PU L#3 (P#13)
L2 L#2 (512KB) + L1d L#2 (32KB) + L1i L#2 (64KB) + Core L#2
PU L#4 (P#2)
PU L#5 (P#14)
L3 L#1 (8192KB)
L2 L#3 (512KB) + L1d L#3 (32KB) + L1i L#3 (64KB) + Core L#3
PU L#6 (P#3)
PU L#7 (P#15)
L2 L#4 (512KB) + L1d L#4 (32KB) + L1i L#4 (64KB) + Core L#4
PU L#8 (P#4)
PU L#9 (P#16)
L2 L#5 (512KB) + L1d L#5 (32KB) + L1i L#5 (64KB) + Core L#5
PU L#10 (P#5)
PU L#11 (P#17)
NUMA aware threading
numactl --cpunodebind=1 --membind=1 ./julianumactl --physcpubind=0-5 --membind=0TODO: Ensure that Julia actually obeys numactl
Distributed
Distributed processing in Julia uses individual processes that communicated with each other.
This allows for computation to scale across data centers instead of just running on one machine.
Data movement and communication is explicit
Master-Worker model
julia -p 4 # Start Julia with 4 local processes
julia> addprocs(4) # Add 4 local processes
julia> nprocs()
5
julia> nworkers()
4
julia> myid()
1
julia> workers()
[2, 3, 4, 5]
# remotecall will not block
julia> f = remotecall(myid, 2)
Future(2, 1, 6, Nullable{Any}())
julia> wait(f)
# Note: `fetch` will `wait` on the value being available
julia> fetch(f)
2Master-Worker model
# `wait` and `fetch` require multiple messages
# to be send over the network. For efficiency
# two variants are provided.
# * remotecall_wait = wait(remotecall())
# * remotecall_fetch = fetch(remotecall())
julia> remotecall_wait(x->2x, 4, 2)
# Closures get serialized
julia> g(x) = 2x
julia> remotecall_fetch(g, 3, 2)
ERROR: On worker 3:
UndefVarError: #g not defined
...
# Methods are not.
julia> @everywhere g(x) = 2x
julia> remotecall_fetch(g, 3, 2)
4
An Excursion: Tasks
@sync begin
@async (sleep(3); println("Today is reverse day!"))
@async (sleep(2); println(" class!"))
@async print("Hello")
end
@sync begin
for wid in workers()
@async remotecall_wait(println, wid, "Hello from worker ", string(wid))
end
endMaster-Worker model
# Use `@verywhere` to execute a top-level block on each process
@everywhere begin
using Test
include("src.jl")
end
# Define on all processes the variable bar
@everywhere bar = 1
julia> foo = 10
julia> @everywhere baz = $fooMaster-Worker model
help?> @parallel
A parallel for loop of the form :
@parallel [reducer] for var = range
body
end
The specified range is partitioned and locally executed
across all workers. In case an optional reducer function
is specified, @parallel performs local reductions on each
worker with a final reduction on the calling process.
Note that without a reducer function, @parallel
executes asynchronously, i.e. it spawns independent tasks
on all available workers and returns immediately without waiting
for completion. To wait for completion, prefix the call with
@sync, like :
@sync @parallel for var = range
body
endjulia> pmap(f, data) # chunk up data and distribute work across workers
# Better use DistributedArrays.jlMaster-Worker model
We get little benefit if we are not able to launch processes on other machines
- Julia has an inbuilt SSH connection
- For integration with various Cluster environments use https://github.com/JuliaParallel/ClusterManagers.jl
addprocs([("anubis.juliacomputing.io", 4)],
exename="/data/vchuravy/julia/julia",
dir="/data/vchuravy")DistributeArrays.jl
Instead of using remote procedure calls we can use DArrays, to distribute data and efficiently compute across processes.
DistributeArrays.jl
@everywhere using DistributedArrays
# Distribute local array across processes
distribute(a::Array)
# Convert a distributedArray to a local one
convert(Array, a::DArray)
# access the process local part of the DArray
localpart(dA::DArray)
dA[:L]
# Which indexes are local?
localindexes(a::DArray)
# Construct a distributed array
julia> dA = dfill(0.0, 500, 500)
julia> remotecall_fetch(()->size(localpart(dA)), 2)
(250, 250)
julia> remotecall_fetch(localindexes, 3, dA)
(251:500, 1:250)
# Darray(init, dims, [procs, dist])
julia> dA = dfill(1.0, (128, 128), workers(), [1, nworkers()]);
julia> remotecall_fetch(()->size(localpart(dA)), 2)
(128, 32)DistributeArrays.jl
function Base.map!{F}(f::F, dest::DArray, src::DArray)
@sync for p in procs(dest)
@async remotecall_wait(p) do
map!(f, localpart(dest), src[localindexes(dest)...])
nothing
end
end
return dest
end
Noteworthy packages
- https://github.com/JuliaParallel/Dagger.jl
- https://github.com/JuliaParallel/Elemental.jl
- https://github.com/JuliaParallel/MPI.jl
- https://github.com/JuliaParallel/PageRankBenchmark
MPI.jl
import MPI
MPI.Init()
comm = MPI.COMM_WORLD
MPI.Barrier(comm)
root = 0
r = MPI.Comm_rank(comm)
sr = MPI.Reduce(r, MPI.SUM, root, comm)
if(MPI.Comm_rank(comm) == root)
@printf("sum of ranks: %s\n", sr)
end
MPI.Finalize()mpirun -np 4 ./julia example.jlAccelerated computing
Based on the 2016 slides prepared by Tim Besard (UGent, Belgium) and Valentin Churavy
https://github.com/alanedelman/18.337_2016/blob/master/lectures/lecture_6_09_26/20160926-mit_gpu_class.pdf
CPU die shot
https://en.wikichip.org/wiki/intel/microarchitectures/coffee_lake
Many-Core die shot
https://en.wikichip.org/wiki/pezy/pezy-sc
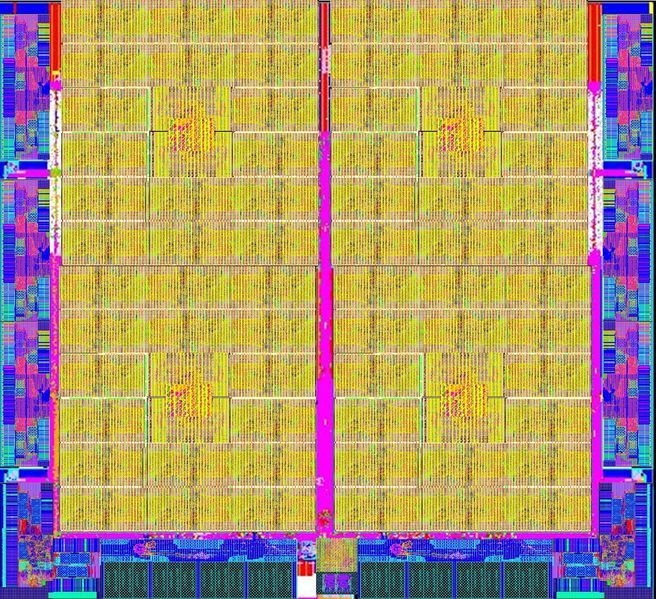
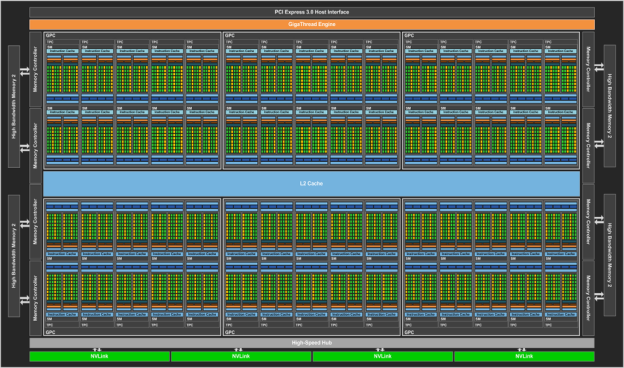
P100 block-diagram
https://devblogs.nvidia.com/parallelforall/inside-pascal/
How do GPU works
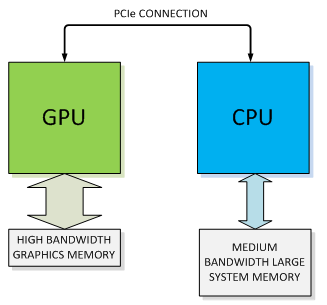
Source: NVIDIA
Slow!
Fast!
Fast!
Device
Host
How do GPU works
Source: AllegroViva
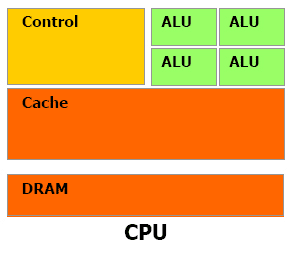
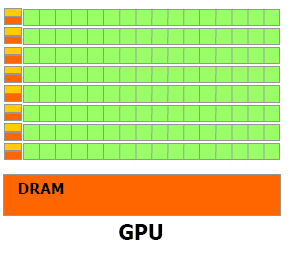
Heavyweight cores
Limited parallelism
Advanced control circuits:
- out of order execution
- branch prediction
Lightweight cores -> higher latency
Massive parallelism
How do GPU works
Latency hiding
Source: TU/e

Requirement: Enough work to schedule (occupancy)
How do GPU works
Source: AllegroViva


Heavyweight cores
Limited parallelism
Advanced control circuits:
- out of order execution
- branch prediction
Lightweight cores -> higher latency
Massive parallelism
Simplified, shared control circuitry
- Lockstep execution
How do GPU works
lockstep execution
Source: Y. Kreinin
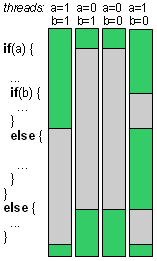
How do GPU works
- Massive parallelism
-
Lightweight cores
- High latency
-
Latency hiding given sufficient occupancy
-
Lockstep execution
- Avoid branch divergence
- Memory transfer cost
How to program GPUs
So far in this class we have been using library abstractions like:
- CuArrays.jl
- GPUArrays.jl
- ArrayFire
- CuBLAS.jl
Using libraries you will get good performance in most cases, but what do you do if what you need is not implemented and you can't write it as a broadcast?
How to program GPUs
function cpu_vadd(a, b, c)
for i = 1:length(a)
c[i] = a[i] + b[i]
end
end
len = 16
a = rand(len)
b = rand(len)
c = similar(a)
cpu_vadd(a, b, c)function gpu_vadd(a, b, c)
i = get_my_index()
c[i] = a[i] + b[i]
end
len = 16
a = rand(len)
b = rand(len)
gpu_a = CuArray(a)
gpu_b = CuArray(b)
gpu_c = CuArray(Float64, len)
@cuda (...) gpu_vadd(gpu_a, gpu_b, gpu_c)
c = Array(d_c)How to program GPUs
function gpu_vadd(a, b, c)
i, j = threadIdx().x, threadIdx().y
c[i,j] = a[i,j] + b[i,j]
end
threads = (size(a,1), size(a,2))
@cuda (1,threads) gpu_vadd(...)get_my_index() ?
threadIdx() & blockDim()
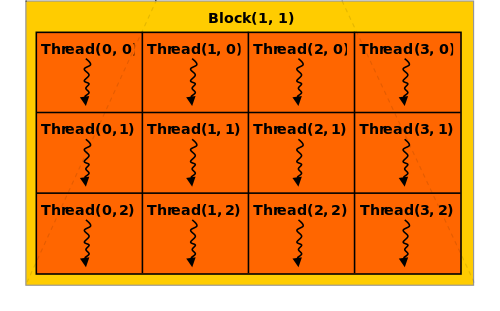
@cuda (1, threads) kernel(...)How to program GPUs
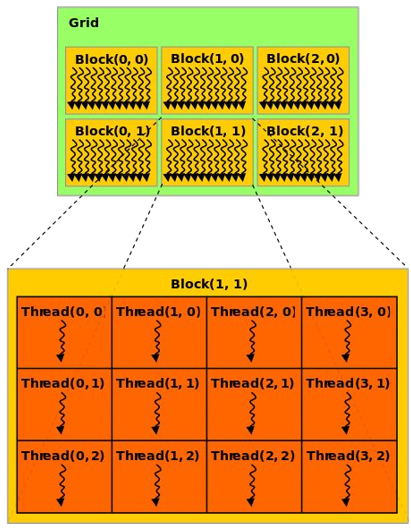
Threads are executed together
- Cheaper communication
- Lockstep execution
threadIdx(), blockDim()
blockIdx(), gridDim()
@cuda (blocks, threads) kernel(...)Source: NVIDIA/AllegroViva
How to program GPUs
prefix sum
function cpu_scan{T}(data)
cols = size(data,2)
for col in 1:cols
accum = zero(T)
rows = size(data,1)
for row in 1:rows
accum += data[row,col]
data[row,col] = accum
end
end
end
4×4 Array{Int64,2}:
1 5 9 13
2 6 10 14
3 7 11 15
4 8 12 16
4×4 Array{Int64,2}:
1 5 9 13
3 11 19 27
6 18 30 42
10 26 42 58How to program GPUs
prefix sum
function cpu_scan{T}(data)
cols = size(data,2)
for col in 1:cols
accum = zero(T)
rows = size(data,1)
for row in 1:rows
accum += data[row,col]
data[row,col] = accum
end
end
end
function gpu_scan{T}(data)
cols = gridDim().x
col = blockIdx().x
rows = blockDim().x
row = threadIdx().x
accum = zero(T)
for i in 1:row
accum += data[i,col]
end
data[row,col] = accum
end
@cuda (size(data,2), size(data,1)) gpu_scan(...)
How to program GPUs
prefix sum
function gpu_scan{T}(data)
cols = gridDim().x
col = blockIdx().x
rows = blockDim().x
row = threadIdx().x
accum = zero(T)
for i in 1:row
accum += data[i,col]
end
data[row,col] = accum
end
@cuda (size(data,2), size(data,1)) gpu_scan(...)
4×4 Array{Int64,2}:
1 5 9 13
2 6 10 14
3 7 11 15
4 8 12 164×4 Array{Int64,2}:
1 5 9 13
2 6 10 14
3 7 30 15
4 8 12 16sync_threads()Branch divergence
Our vision
CUDAnative.jl should be easy to use and install on Julia 1.0 and top of that we want to build an GPU ecosystem that is easily extendable and flexible.
A = CuArray(...)
B = CuArray(...)
myfun(x) = sin(2x) + cos(3x)
C .= A .+ myfun.(B)As an example broadcast/dot-fusion vastly simplifies using GPU resources for vectorizable code.
Research question: How do we generalize this to more complicated data movement patterns
Multiple GPUs
CUDA support multiple execution contexts.
using CUDAdrv
@show CUDAdrv.devices
ctx0 = CuContext(CuDevice(0))
ctx1 = CuContext(CuDevice(1))
activate(ctx0)
# Async schedule kernel calls
activate(ctx1)
# Async schedule kernel calls
http://www.nvidia.com/docs/IO/116711/sc11-multi-gpu.pdf
We currently don't have nice APIs, so help is welcome.
What does your processor actually do
Coming Wednesday!
IACA.jl
Coming Wednesday!
perf
Coming Wednesday!
Resources
Coming Wednesday!
- Chandlers talk
- agner
julia-parallelism
By Valentin Churavy
julia-parallelism
- 5,029
