Coding data and making inferences in regression

PSY 716

Single-predictor linear regression

where:

• \(Y_i\) is the dependent variable
• \(X_i\) is the independent variable (group membership or continuous covariate)
• \(\beta_0\) is the intercept
• \(\beta_1\) is the regression coefficient
• \(\epsilon_i\) is the error term

$$ Y_i = \beta_0 + \beta_1 X_i + \epsilon_i $$

Multivariate linear regression with five predictors

where:

• \(y_i\) is the dependent variable
• \(x_{i1} ... x_{i5}\) are independent variables
• \(\beta_0\) is the intercept
• \(\beta_j\) is the regression coefficient for variable \(j\)
• \(\epsilon_i\) is the error term

$$ y_i = \beta_0 + \beta_1 x_{i1} + $$

$$ \beta_2 x_{i2} + \beta_3 x_{i3} + \beta_4 x_{i4} + \beta_5 x_{i5} + \epsilon_i $$

The linear regression model predicted a significant portion of the variance in our outcome, \(R^2 = .709, F(5, 94) = 45.8, p < .001\). The predictor \(x_1\) was significantly positively linked to our outcome, \(\beta_1 = 0.459, t(94) = 5.12, p < .001\) And so on...

As a reminder:

• Relevant df:
  • Model/regression df = k, where k is the number of predictors
  • Error/residual df = N - k - 1
• Relevant test statistics
  • F(Model df, error df)
  • t(error df)

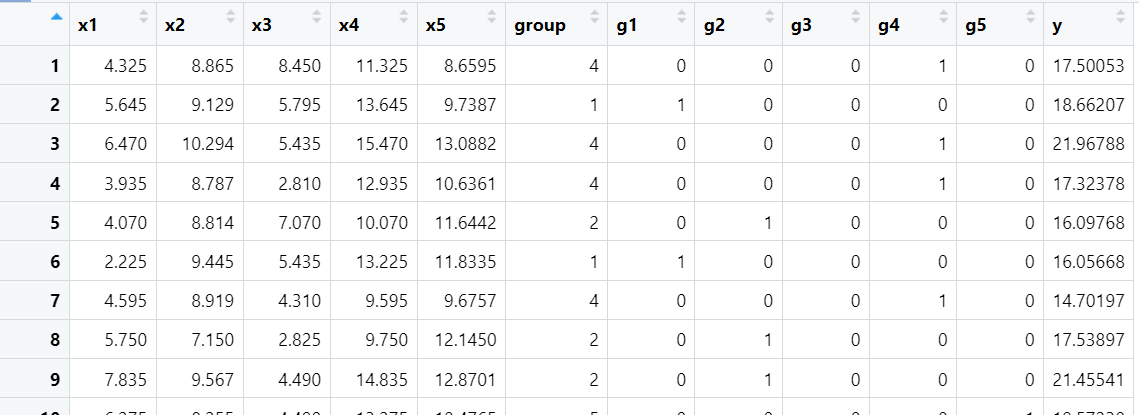
Multivariate linear regression with four predictors which are dummy codes for a five-level independent variable

where:

• \(y_i\) is the dependent variable
• \(g_{i1} ... g_{i4}\) are dummy codes for a 5-level independent variable
• \(\beta_0\) is the intercept
• \(\beta_j\) is the regression coefficient for variable \(j\)
• \(\epsilon_i\) is the error term

$$ y_i = \beta_0 + \beta_1 g_{i1} + \beta_2 g_{i2} + \beta_3 g_{i3} + \beta_4 g_{i4} $$

What does each of these coefficients mean????

As a reminder:

• Relevant df:
  • Model/regression df = k, where k is the number of predictors
  • Error/residual df = N - k - 1
• Relevant test statistics
  • F(Model df, error df)
  • t(error df)

18.75831 - (-0.1032) = 18.65508

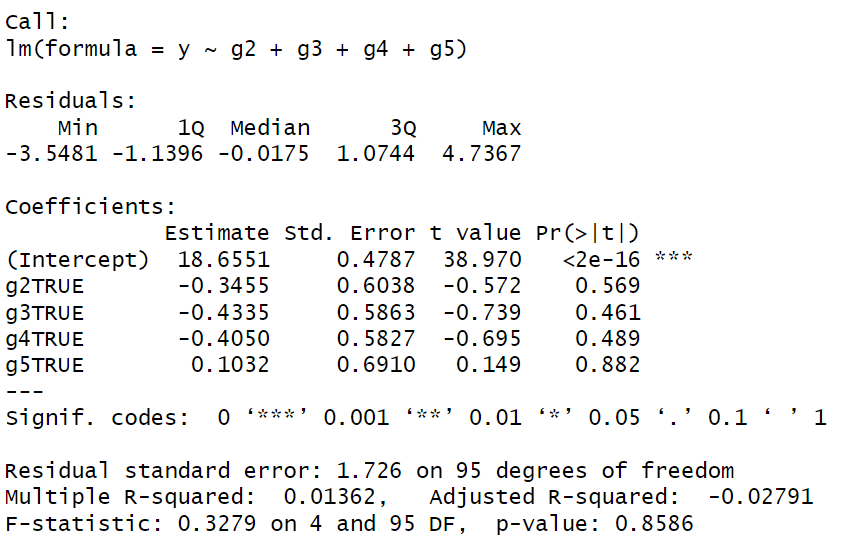
What if we chose a different reference category?

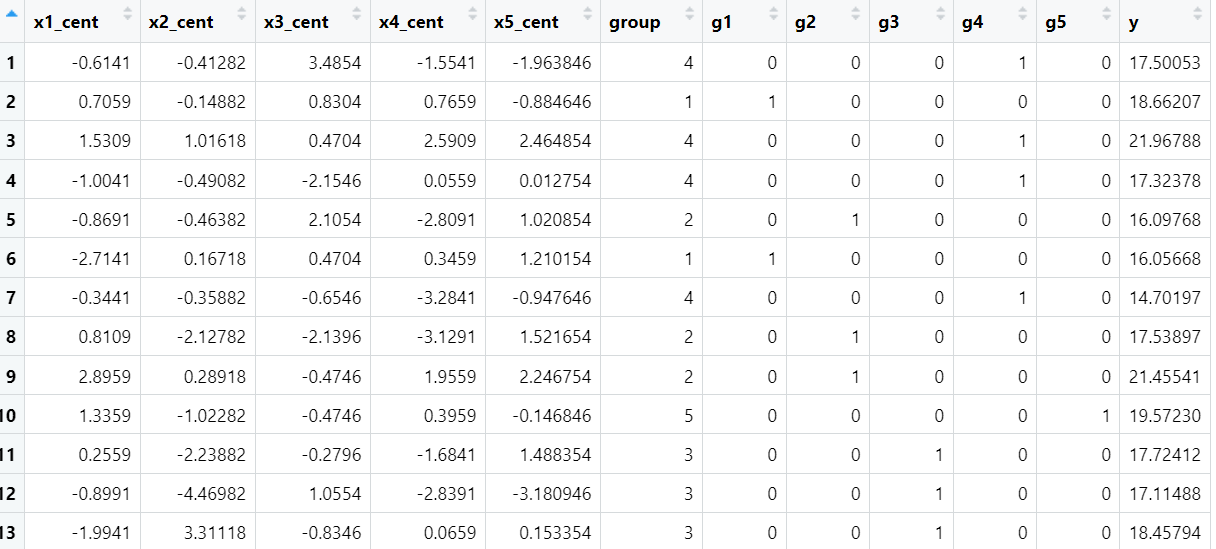
Multivariate linear regression with five predictors, which are centered

where:

• \(y_i\) is the dependent variable
• \(\"{x}_{i1} ... \"{x}_{i5}\) are centered independent variables
• \(\beta_0\) is the intercept
• \(\beta_j\) is the regression coefficient for variable \(j\)
• \(\epsilon_i\) is the error term

$$ y_i = \beta_0 + \beta_1 \"{x}_{i1} + $$

$$ \beta_2 \"{x}_{i2} + \beta_3 \"{x}_{i3} + \beta_4 \"{x}_{i4} + \beta_5 \"{x}_{i5} $$

N.B. Putting dots on top of predictors isn't necessary -- just want to denote them a different way here!

What does each of these coefficients mean????

As a reminder:

• Relevant df:
  • Model/regression df = k, where k is the number of predictors
  • Error/residual df = N - k - 1
• Relevant test statistics
  • F(Model df, error df)
  • t(error df)

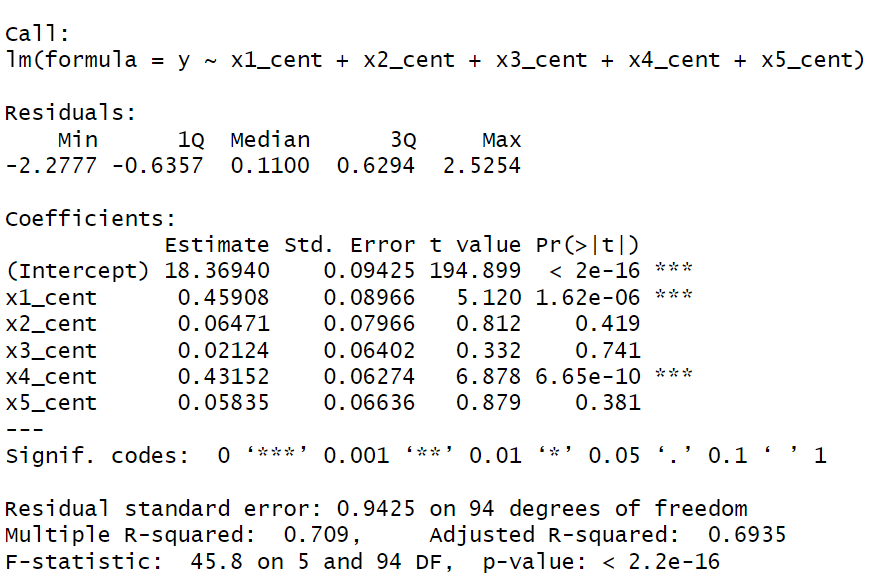
Uncentered

Centered

You may be wondering: Why are we doing all of this? 

The goal is to build up to arbitrarily complex stuff, like this:

Multivariate linear regression with five predictors, four of which are levels of a categorical predictor, and an interaction between the categorical predictor and the continuous predictor (yikes)

where:

• \(Y_i\) is the dependent variable
• \(X_{i1}\) is an independent variable
• \(X_{i2} ... X_{i5}\) are dummy codes for another independent variable
• \(\beta_0\) is the intercept
• \(\beta_j\) is the regression coefficient for the \(j^{th}\) term
• \(\epsilon_i\) is the error term

$$ Y_i = \beta_0 + \beta_1 x_{i1} + $$

$$ \beta_2 x_{i2} + \beta_3 x_{i3} + \beta_4 x_{i4} + \beta_5 x_{i5} + $$

$$ \beta_6 x_{i1}x_{i2} + \beta_7 x_{i1}x_{i3} + \beta_8 x_{i1}x_{i4} + \beta_9 x_{i1}x_{i5} + \epsilon_i $$