207 demography
Vincent DUSAUTOIR
Antoine FORET
Sommaire
- Présentation
- Les calculs
- Exploitation du projet
Présentation
LES CALCULS
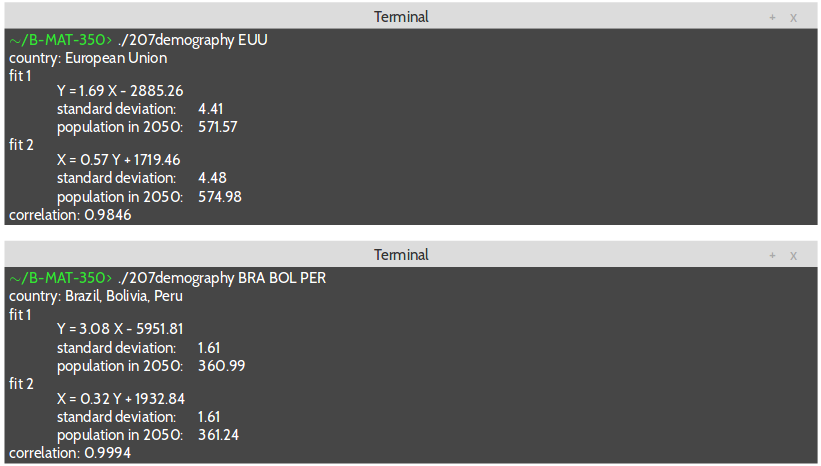
y = ax + b
b
a
Les calculs
\bar{X} = \frac{\sum x}{n}
\bar{Y} = \frac{\sum y}{n}
Cov(x,y) = \bar{XY} - \bar{X} * \bar{Y}
\bar{XY} = \frac{\sum xy}{n}
La covariance permet d’étudier les variations simultanées de deux variables par rapport à leur moyenne respective.
Les calculs
V(X) = \bar{X^{2}} - \bar{X}^{2}
La variance est une mesure servant à caractériser la dispersion d’une distribution ou d’un échantillon.
\bar{X} = \frac{\sum x}{n}
\bar{Y} = \frac{\sum y}{n}
\bar{XY} = \frac{\sum xy}{n}
V(Y) = \bar{Y^{2}} - \bar{Y}^{2}
Les calculs
r = \frac {Cov(x,y)} {\sqrt {V(X) V(Y)}}
Le coefficient de correlation étudie l'intensité de la liaison qui peut exister entre deux variables
\bar{X} = \frac{\sum x}{n}
\bar{Y} = \frac{\sum y}{n}
\bar{XY} = \frac{\sum xy}{n}
Les calculs
a = \frac {Cov(x, y)} {V(X)}
b = \bar {Y} - a - \bar {X}
\sigma = \frac {\sum {(E-R)^{2}}} {n}
y = a * year + b
Recherche de la popultaion
Les calculs
a = \frac {Cov(x, y)} {V(Y)}
b = \bar {X} - a - \bar {Y}
\sigma = \frac {\sum {(E-R)^{2}}} {n}
x = \frac {(pop - b)} {a}
Recherche de l'année
Exploitation
des résultats
question
207
By vdnet
