Riga Technical University
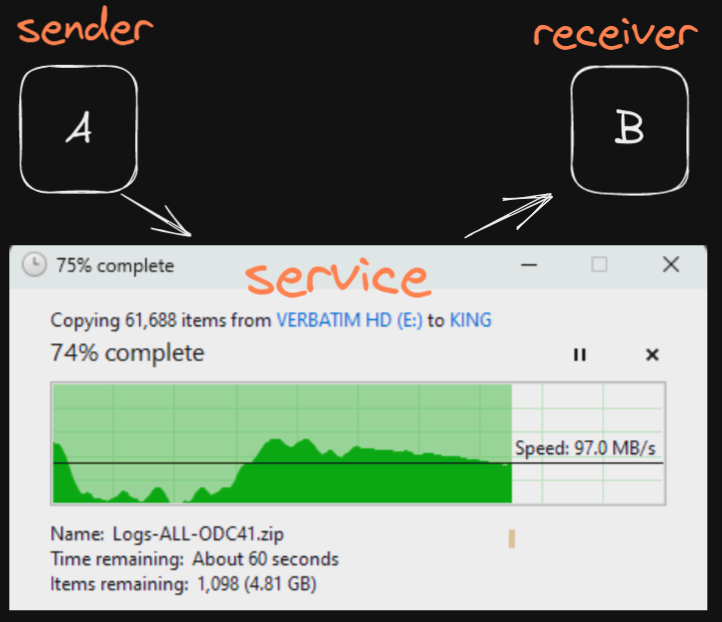
WHERE is the TELE-TRAFFIC here?
PROBLEM Nr1
WHERE is the TELE-TRAFFIC here?
PROBLEM Nr2
Digital Communication Flow in
Parcel Service
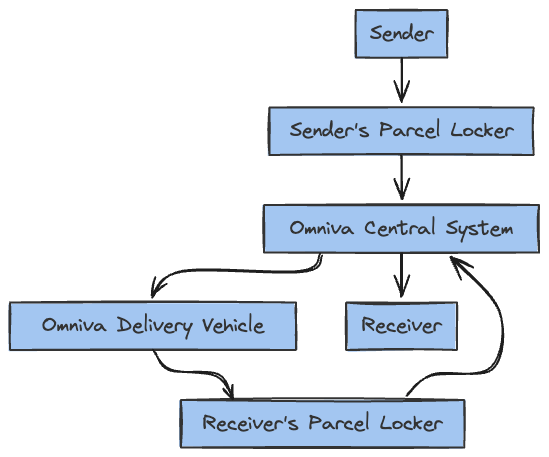
WHERE is the TELE-TRAFFIC here?
PROBLEM Nr3
Course (RAE-555) Life-Span
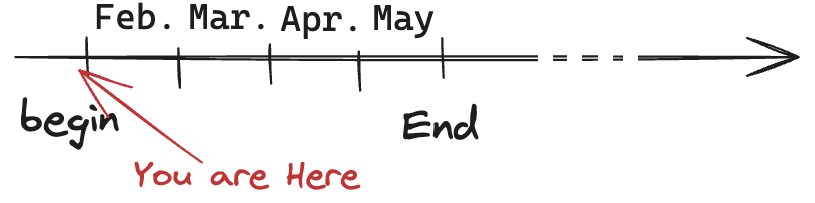
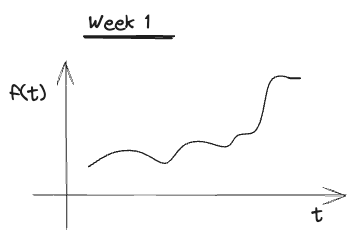
Week 1
2024.01.29
Course (RAE-555) Life-Span
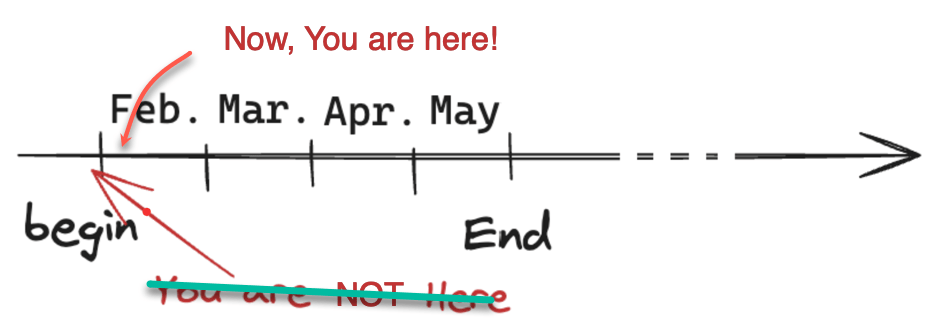
Week 1
Week 2
2024.01.29
2024.02.05
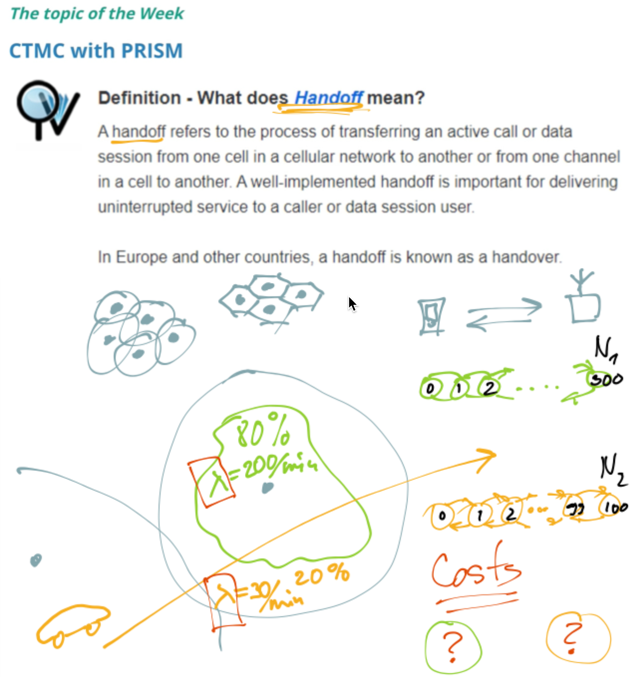
WHERE is the TELE-TRAFFIC in this MODEL?
PROBLEM Nr4
WHAT is the TRAFFIC?
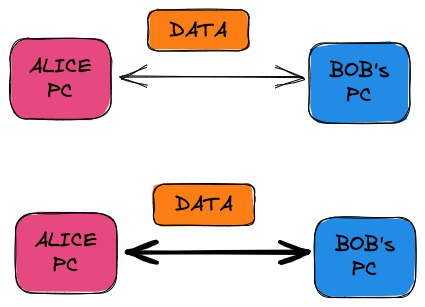
a)
b)
PROBLEM Nr5
HOW
TELE-TRAFFIC THEORY
is HELPFUL for US ?
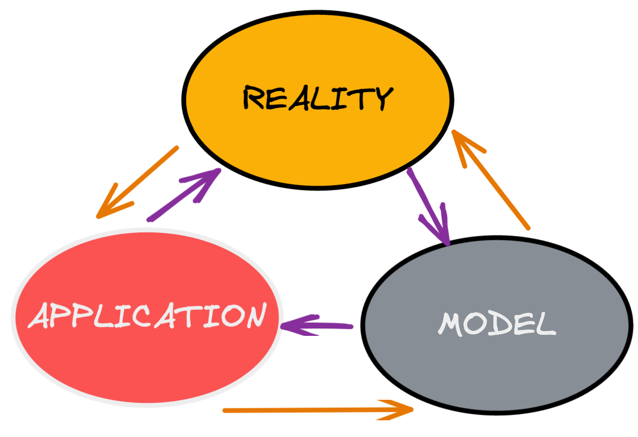
THEORY
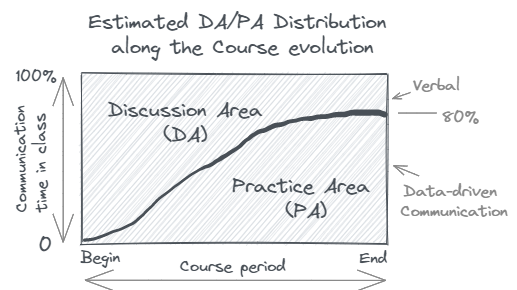
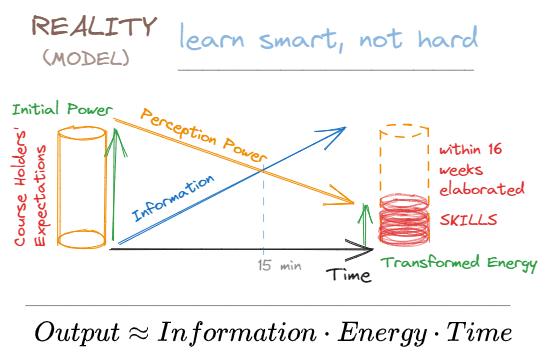
BUSINESS-ORIENTED LEARNING MODEL
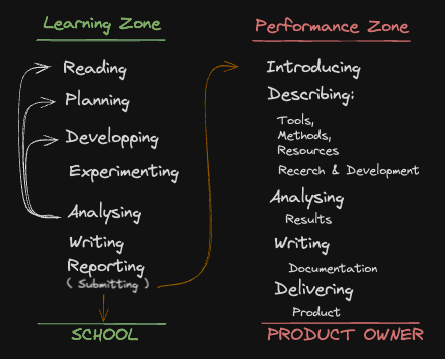
BUSINESS-ORIENTED LEARNING MODEL
2024.01.29
2024.05.31
WHAT is the TRAFFIC?
a)
b)
What are the TRAFFIC METRICS?
WHERE is the TRAFFIC?
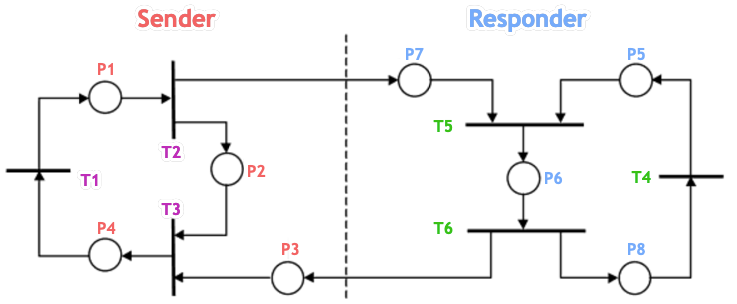
a)
b)
PROBLEM Nr6
What are the TRAFFIC METRICS?
WHERE is the TRAFFIC?
a)
b)
PROBLEM Nr7
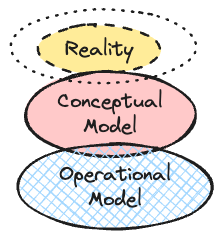
OPERATIONAL
MODEL instantiated as APPLICATION
METRICS & UNITS
OPERATIONAL
MODEL instantiated as APPLICATION
METRICS & UNITS
It's TIME to EXERCISE
PROBLEM Nr8
WEEK 1
Observe & Think
Develop &
Deploy
Run & Relax
Week # 2
Observing
Systems
METRICS
& UNITS
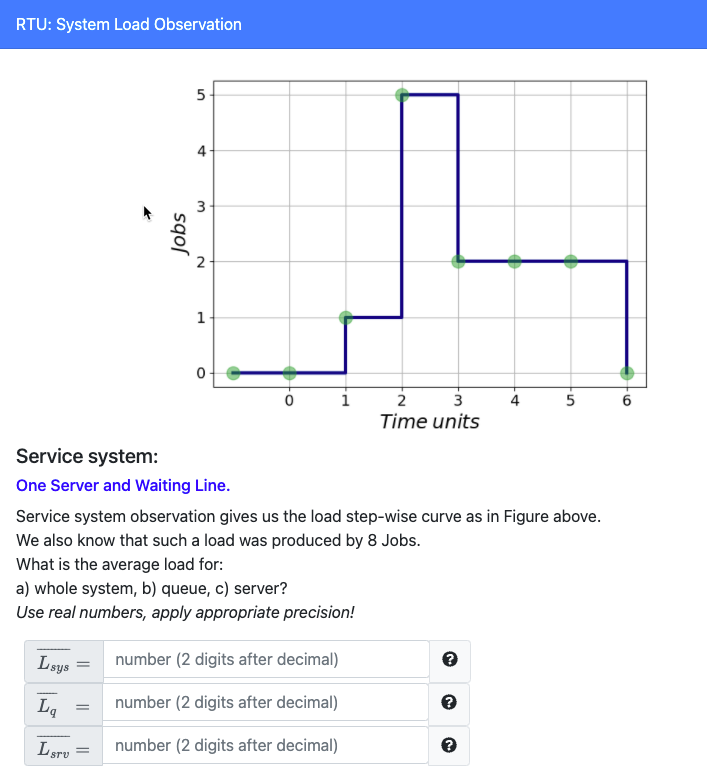
Considering Traffic as a
Service System Load
Dynamic Model
Static Model
What is the queue size?
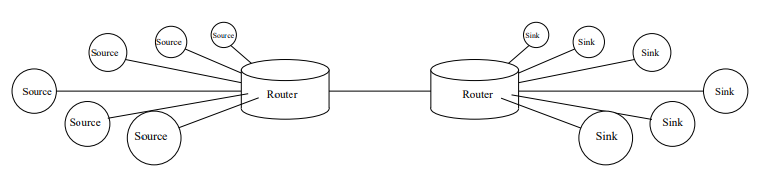
REAL NETWORK MODEL
Considering Traffic as a
Service System Load
What is the router load?
How long will stay the yellow packet in the queue?
How long will be processed the green packet?
W
\overline{W}
T≡
\overline{T} \equiv
N
\overline{N}
L≡
\overline{L} \equiv
TRAFFIC as a
Service System Load
(Jobs, Tasks, Customers, Cars, Data packets, Bytes, etc. )
N=λ⋅W
\overline{N} = \lambda \cdot \overline{W}
Math Model
Conceptual Model
Course Book
https://www.amazon.com/Fundamentals-Queueing-Theory-Probability-Statistics/dp/111894352X/ref=sr_1_6?s=books&ie=UTF8&qid=1510840499&sr=1-6&keywords=fundamentals+of+queueing
Single Node Model
Fundamental Models
N=λ⋅W
\overline{N} = \lambda \cdot \overline{W}
Little's Formula
Fundamental Models
L=λ⋅T
\overline{L} = \lambda \cdot \overline{T}
ρ=μλ
\rho = \frac{\lambda}{\mu}
Erlang's A Formula
Fundamental Models
λ=Tobsk
\lambda = \frac{k}{T_{obs}}
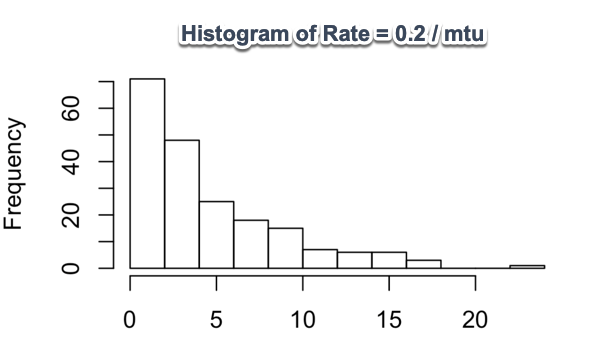
Arrival Rate
Fundamental Models
Tobs→SystemObservationTime
T_{obs} \to System Observation Time
k→CountedArrivedJobs
k \to Counted Arrived Jobs
μ=Tbusyk
\mu = \frac{k}{T_{busy}}
Departure Rate
Fundamental Models
Tbusy→ServerBusyTime
T_{busy} \to Server Busy Time
k→CountedDeparteredJobs
k \to Counted Departered Jobs
W=μ1
\overline{W} = \frac{1}{\mu}
Waiting Time vs Departure Rate
Fundamental Models
μ=W1
\mu = \frac{1}{\overline{W}}
ρ=μλ
{\rho} = \frac{\lambda}{\mu}
Little formula and Erlang formula
Fundamental Models
N=λ⋅W=λμ1
\overline{N} = \lambda \cdot \overline{W} = \lambda\frac{1}{\mu}
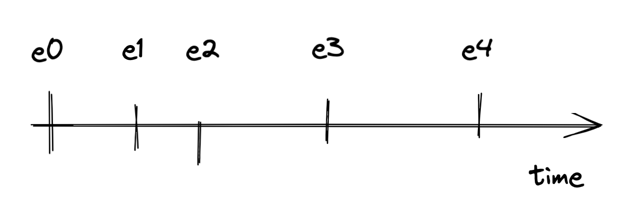
From
OBSERVATION
to
MODEL DATA
Fundamental Models
N=λ⋅W
\overline{N} = \lambda \cdot \overline{W}
ARRIVAL RATE
Fundamental Models
N=λ⋅W
\overline{N} = \lambda \cdot \overline{W}
λ=Tobsk
\lambda = \frac{k} {T_{obs}}
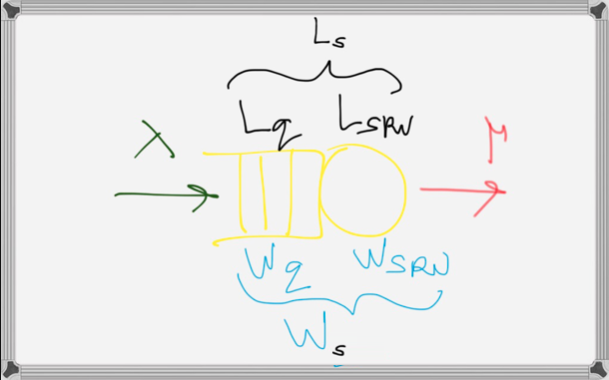
WHERE is the ARRIVAL here?
PROBLEM Nr 2.1
ARRIVAL RATE
Fundamental Models
N=λ⋅W
\overline{N} = \lambda \cdot \overline{W}
λ=Tobsk
\lambda = \frac{k} {T_{obs}}
Problem Domain
Fundamental Models
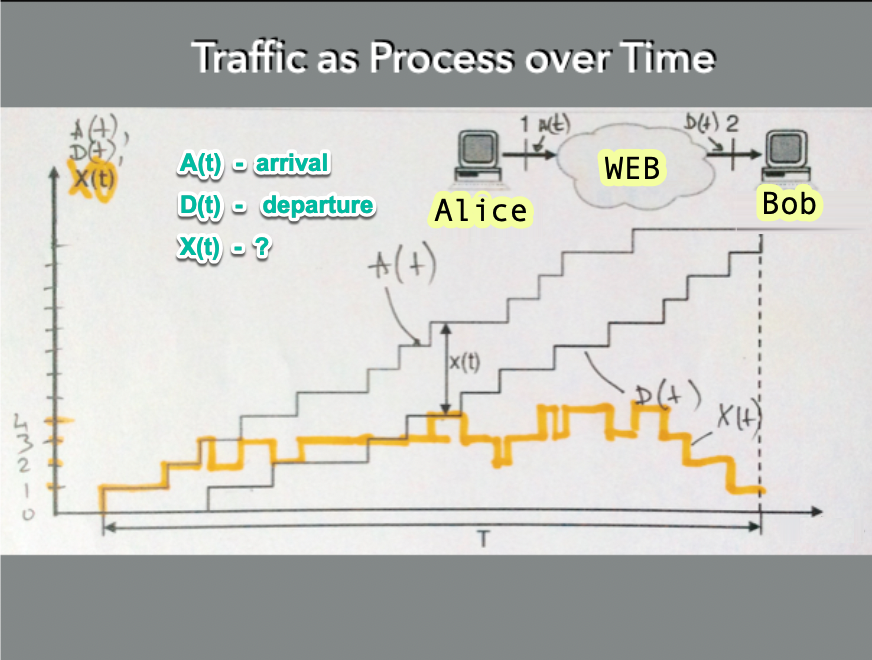
TRAFFIC as a PROCESS over TIME
N=λ⋅W
\overline{N} = \lambda \cdot \overline{W}
N=λ⋅W
\overline{N} = \lambda \cdot \overline{W}
N=λ⋅W
\overline{N} = \lambda \cdot \overline{W}
N=λ⋅W
\overline{N} = \lambda \cdot \overline{W}
N=λ⋅W
\overline{N} = \lambda \cdot \overline{W}
N=λ⋅W
\overline{N} = \lambda \cdot \overline{W}
N=λ⋅W
\overline{N} = \lambda \cdot \overline{W}
N=λ⋅W
\overline{N} = \lambda \cdot \overline{W}
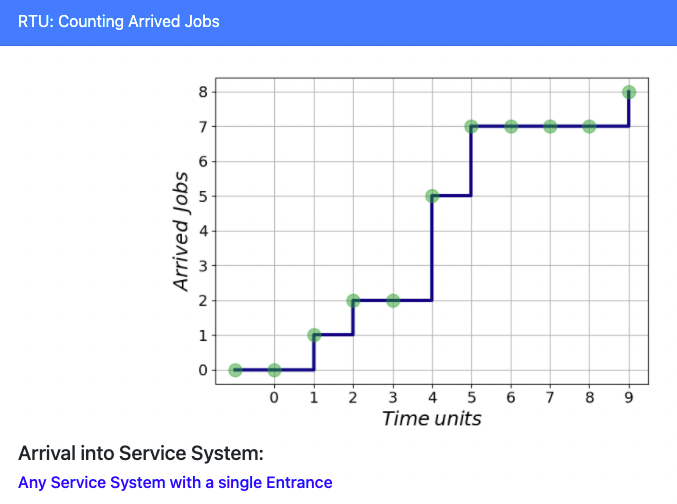
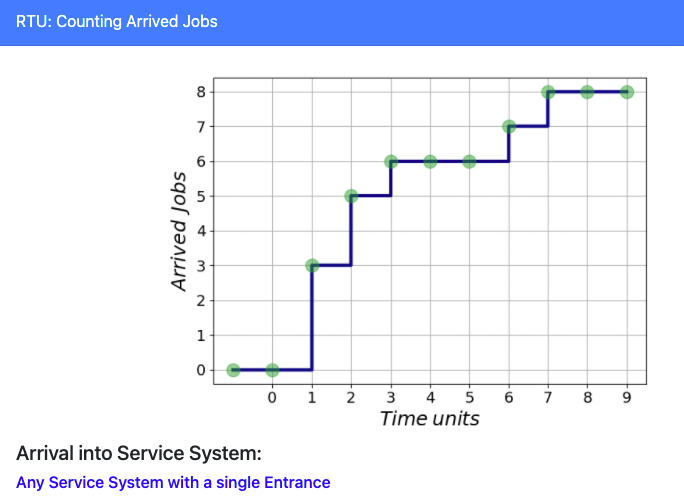
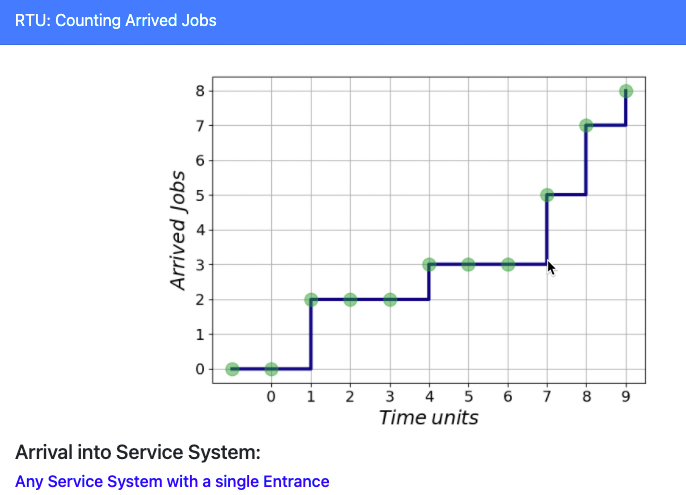
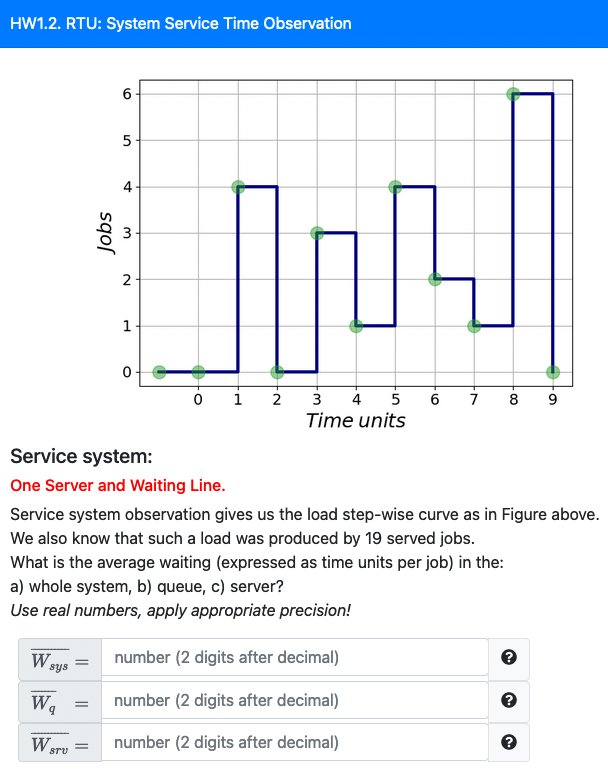
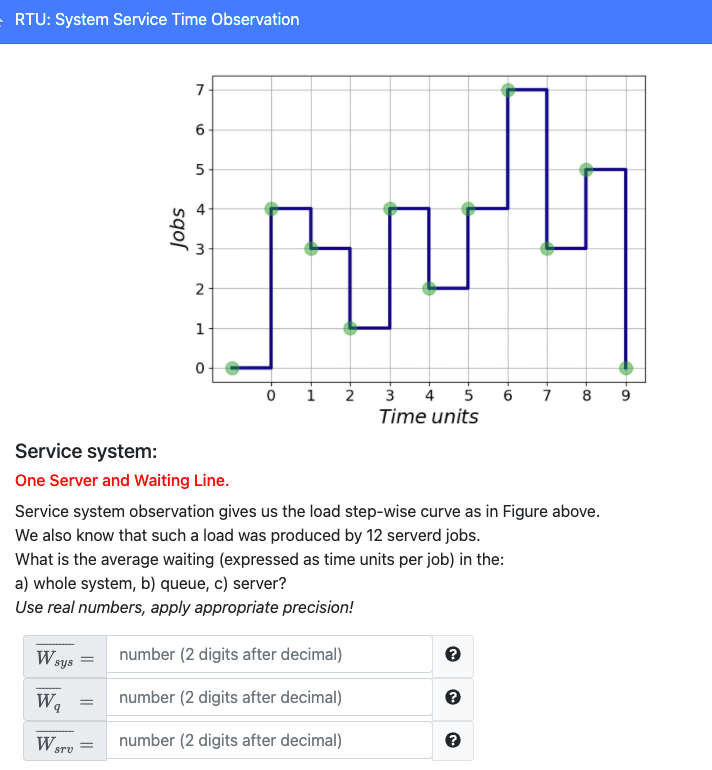
Questions
Fundamental Models
Course Book
https://www.amazon.com/Fundamentals-Queueing-Theory-Probability-Statistics/dp/111894352X/ref=sr_1_6?s=books&ie=UTF8&qid=1510840499&sr=1-6&keywords=fundamentals+of+queueing
Fundamental Models
TRAFFIC as a PROCESS over TIME
PROBLEM Nr9
RTU RAE555
Teletraffic Theory (Spring 2024)
Pre-Class for Week 3
- Choose any service-related Single Node System
- Observe the system for some time
- Analyse the system identifying primary traffic (load-related) characteristics
- Demonstrate results and understanding of the topic:
- Use slides on SLIDES.COM
- Make a Screencast on YouTube or Vimeo (make a short video about the topic)
- Publish the outcome on the course SLACK channel before the next meetup
The output is based on unique and individual experience
Output ( TODO )
Homework
Analysis of a Single Node Service system
(paying attention to the following characteristics)
λ,μ,Nˉsys,Nˉsrv,Nˉqueue,Wˉsys,Wˉsrv,Wˉqueue,k,Tobs,Tbusy
\lambda, \mu, \bar{N}_{sys}, \bar{N}_{srv}, \bar{N}_{queue}, \bar{W}_{sys}, \bar{W}_{srv}, \bar{W}_{queue}, k, T_{obs}, T_{busy}
Just be Active!
Q&A
2024.02.05
Week #3
From Observation to Models
Fundamental Models
N=λ⋅W
\overline{N} = \overline{\lambda} \cdot \overline{W}
Nsys
\overline{N}_{sys}
Wsys
\overline{W}_{sys}
N(t)
N(t)
Wq
\overline{W}_{q}
Wqi
{W}_{q}^i
Wsysi
{W}_{sys}^i
Wqi≡W(i)q
{W}_{q}^i \equiv W(i)_{q}
Client
Server
λ(t)1
\lambda(t)_1
λ(t)2
\lambda(t)_2
μ1
\mu_1
μ2
\mu_2
Fundamental Models
Client
Server
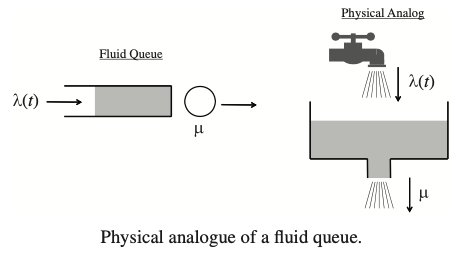
Fundamental Models
Fundamental Models
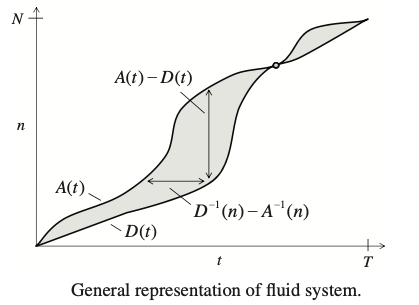
Fundamental Models
T(obs)
T(obs)
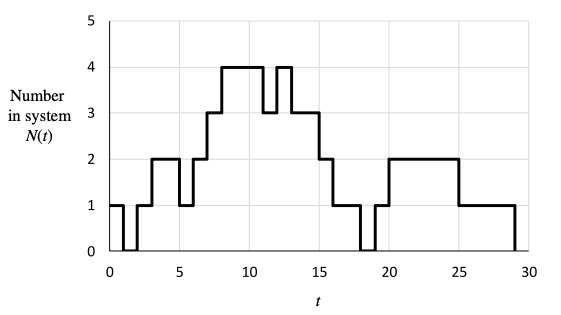
PROBLEM Nr10
Fundamental Models
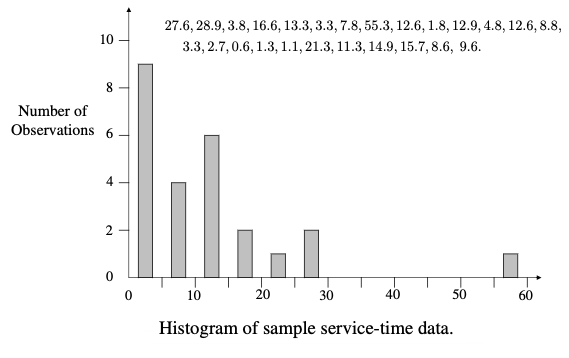
PROBLEM Nr11
Fundamental Models
T(obs)
T(obs)
Fundamental Models
In-Class problem
PROBLEM Nr12
RTU RAE555
Teletraffic Theory (Spring 2024)
In-Class for Week 4
- Analyse the given system identifying primary traffic characteristics
- Demonstrate results and the understanding of the topic:
- Use slides on SLIDES.COM and/or do handwriting + drawing
- Publish the outcome on the course SLACK channel Week-7 before the current Day (2024-xx-xx) ends
- Late submissions are allowed but not welcome.
The output is based on the given problem
Output ( TODO )
Homework
Analysis of a Single Node Service system
(paying attention to the following characteristics)
λ,μ,Nˉsys,Nˉsrv,Nˉqueue,Wˉsys,Wˉsrv,Wˉqueue,k,Tobs,Tbusy
\lambda, \mu, \bar{N}_{sys}, \bar{N}_{srv}, \bar{N}_{queue}, \bar{W}_{sys}, \bar{W}_{srv}, \bar{W}_{queue}, k, T_{obs}, T_{busy}
Week #4
From Observation to Models
2024-02-19
1st Module Exam
POSTPONED
RTU RAE555
Teletraffic Theory (Spring 2024)
Homework for Week 5
- Solve all the given problems related to HW1
- Demonstrate results and understanding of the topic
- Become ready for te Q1
The output is based on unique and individual variants
Output
Homework
Analysis of a Single Node Service system
Week #5
From Observation to Models
2024-02-26
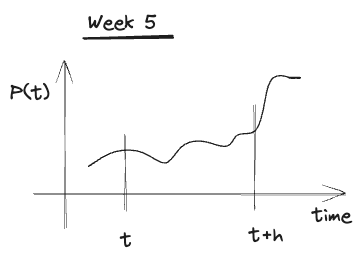
Week 5
Moving towards Reality
Books
P1a(t+h)∼λh
P_{1a}(t+h) \sim \lambda h
P1d(t+h)∼μh
P_{1d}(t+h) \sim \mu h
λ(t)
\lambda (t)
μ(t)
\mu (t)
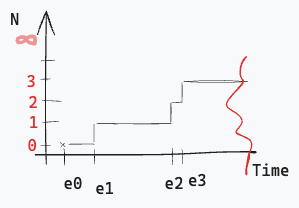
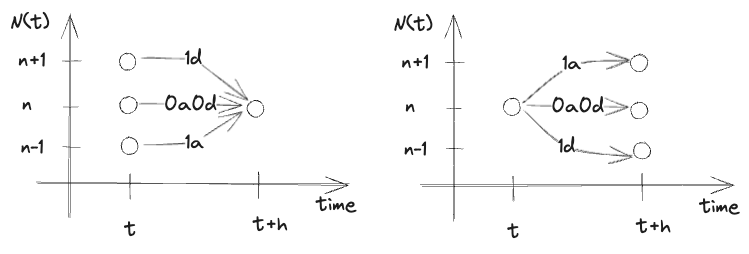
Classwork Time
Week 5
Classwork
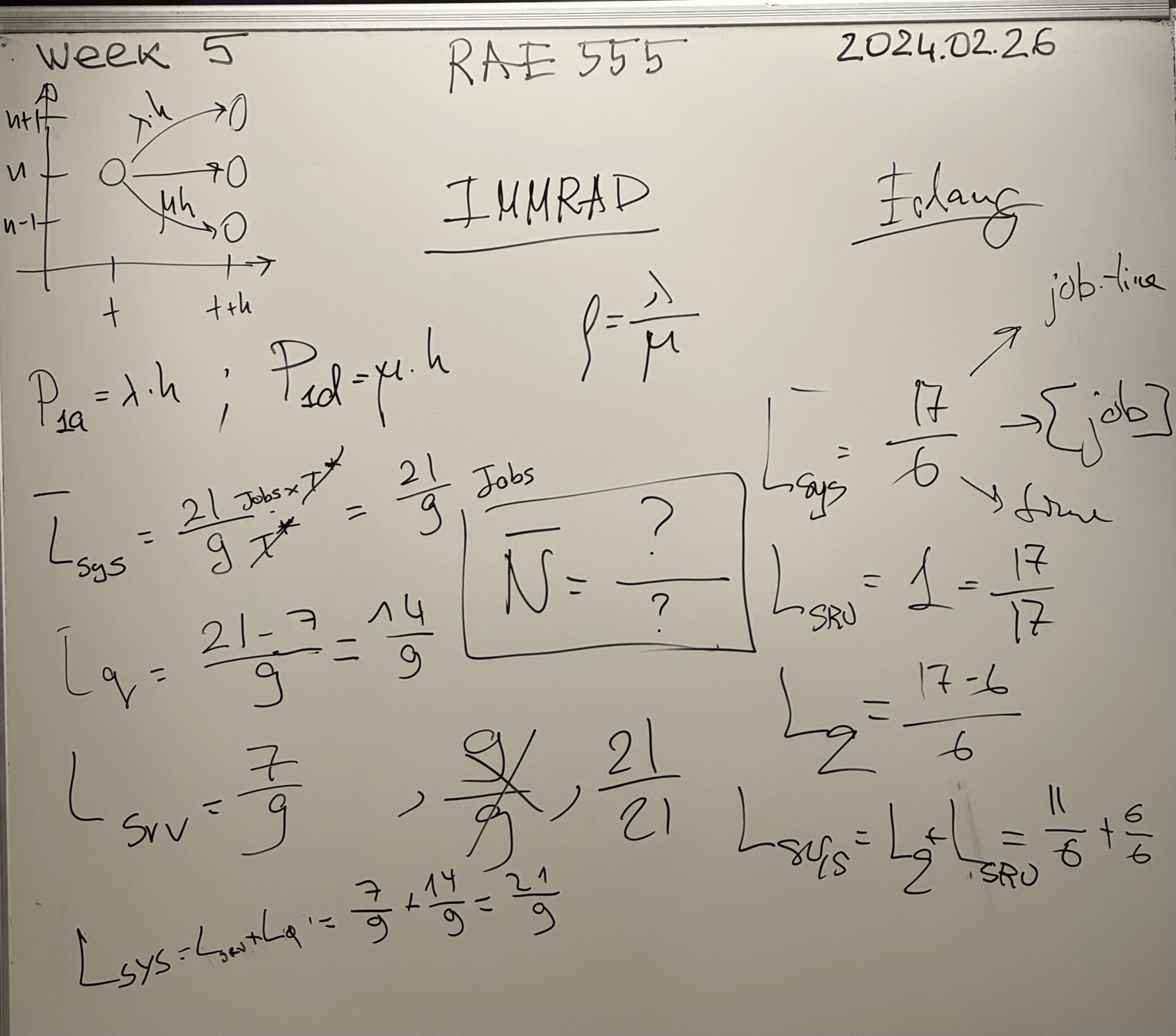
Week 5
Classwork
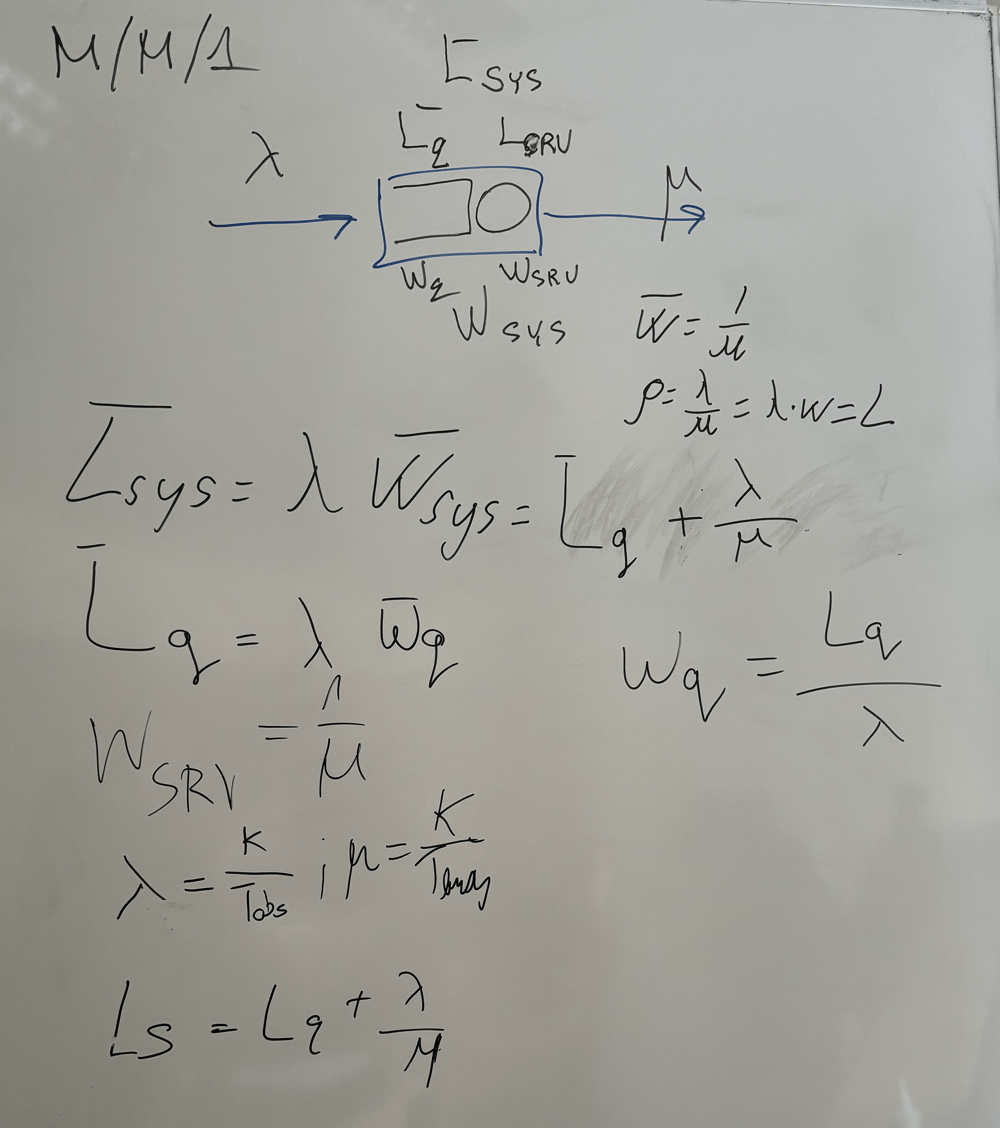
Moving towards Reality
RTU RAE555
Teletraffic Theory (Spring 2024)
Activities for Week 5 (HOMEWORK for Week 6)
- Participate in MADRAS UNI lectures Lec-30 and Lec-31
- Demonstrate understanding of the topic, and namely,
- Publish a recap of both lectures
The output can be complemented by unique and individual variants
Output
Homework
Theoretical Model of a Single Node Service system
TO DO that, proceed to
Week #6
From Observation to Models
2024-03-04
Week 6
Moving towards Reality
Week 6
FINITE SYSTEMS
Building Conceptual Understanding of
DTMC
(Discrete-Time Markov Chains)
Markov Chains
Week 6
FINITE SYSTEMS
DTMC
Markov Chains
CTMC
Books
Challenges
Markov Models
Books
https://www.wiley-vch.de/de/fachgebiete/mathematik-und-statistik/mathematik-16ma/diskrete-mathematik-16ma9/markov-chains-978-1-119-38755-8
Week 6
Homework
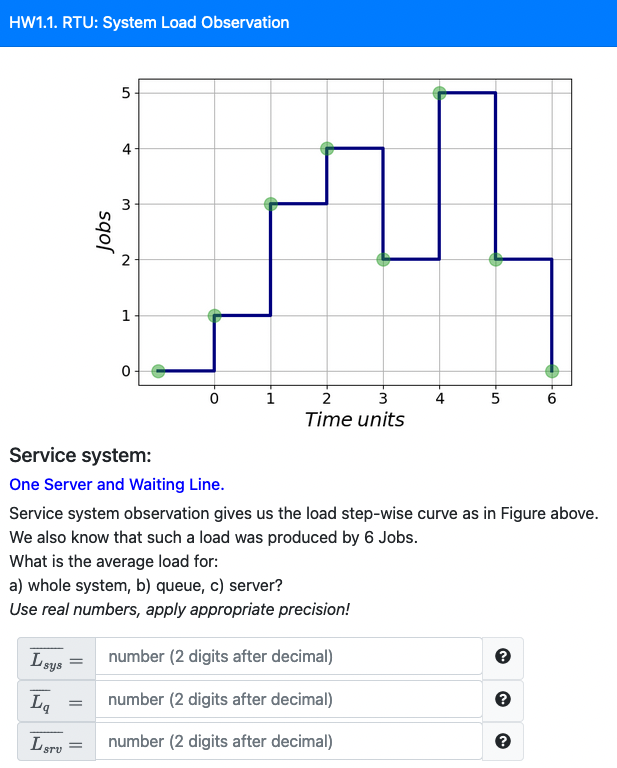
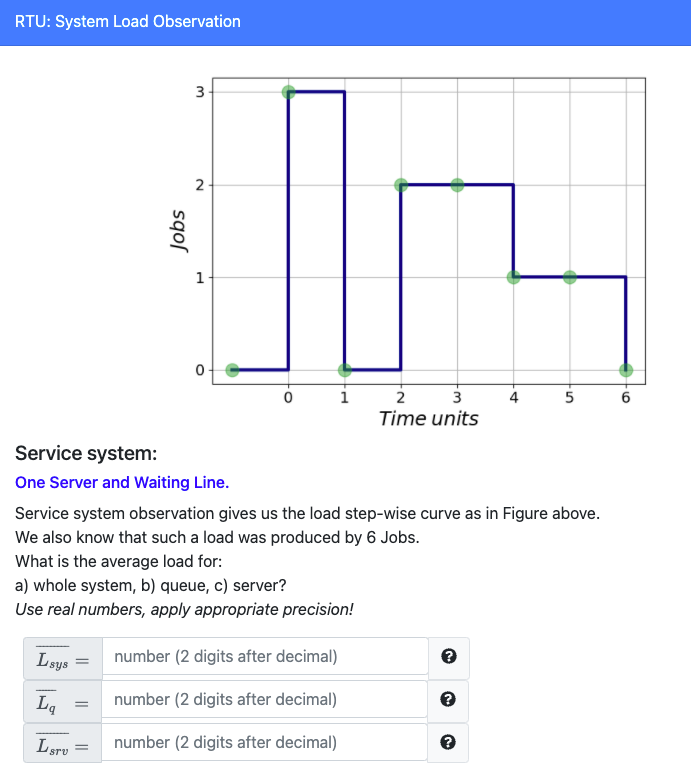
Another viewpoint on load-time model
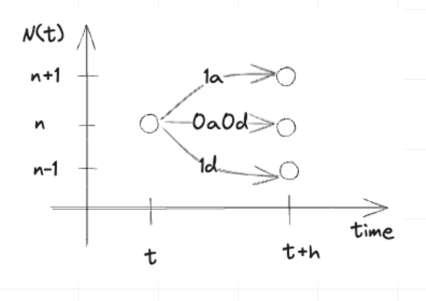
Theoretical Model of a Single Node Service system
In theory, what can you reveal from the model above?
Week 6
Classwork
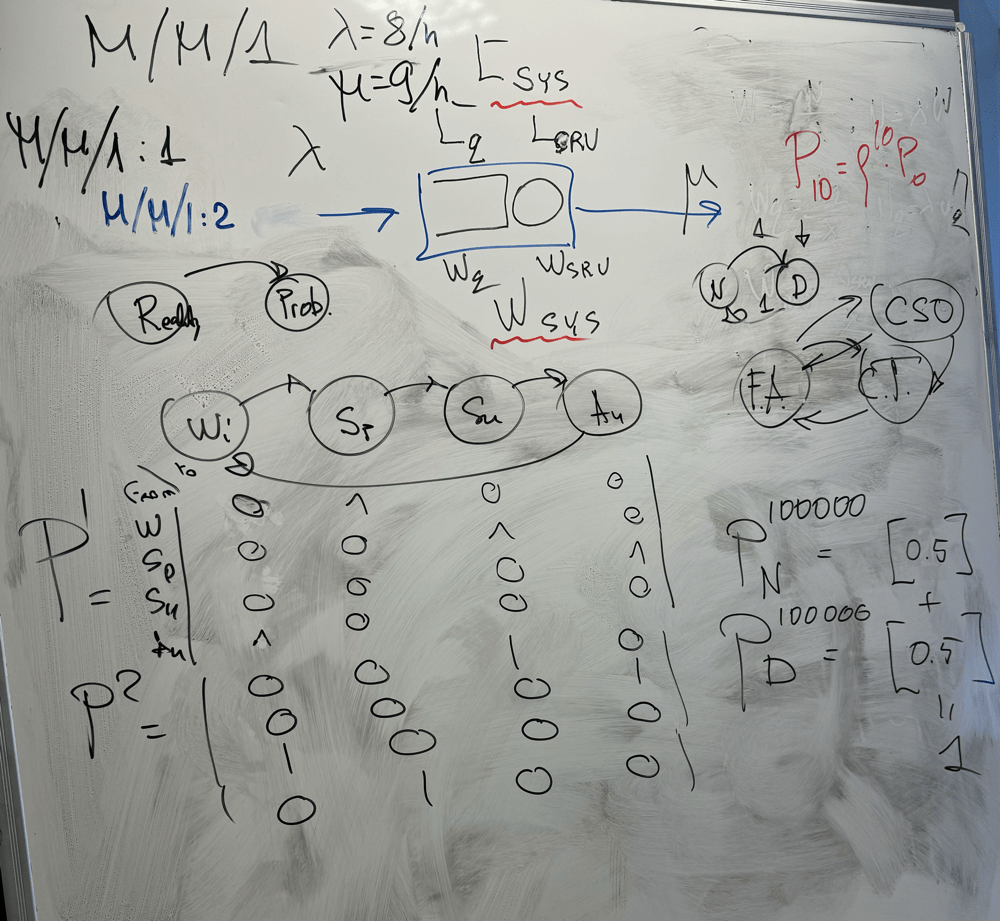
Week 6
Classwork
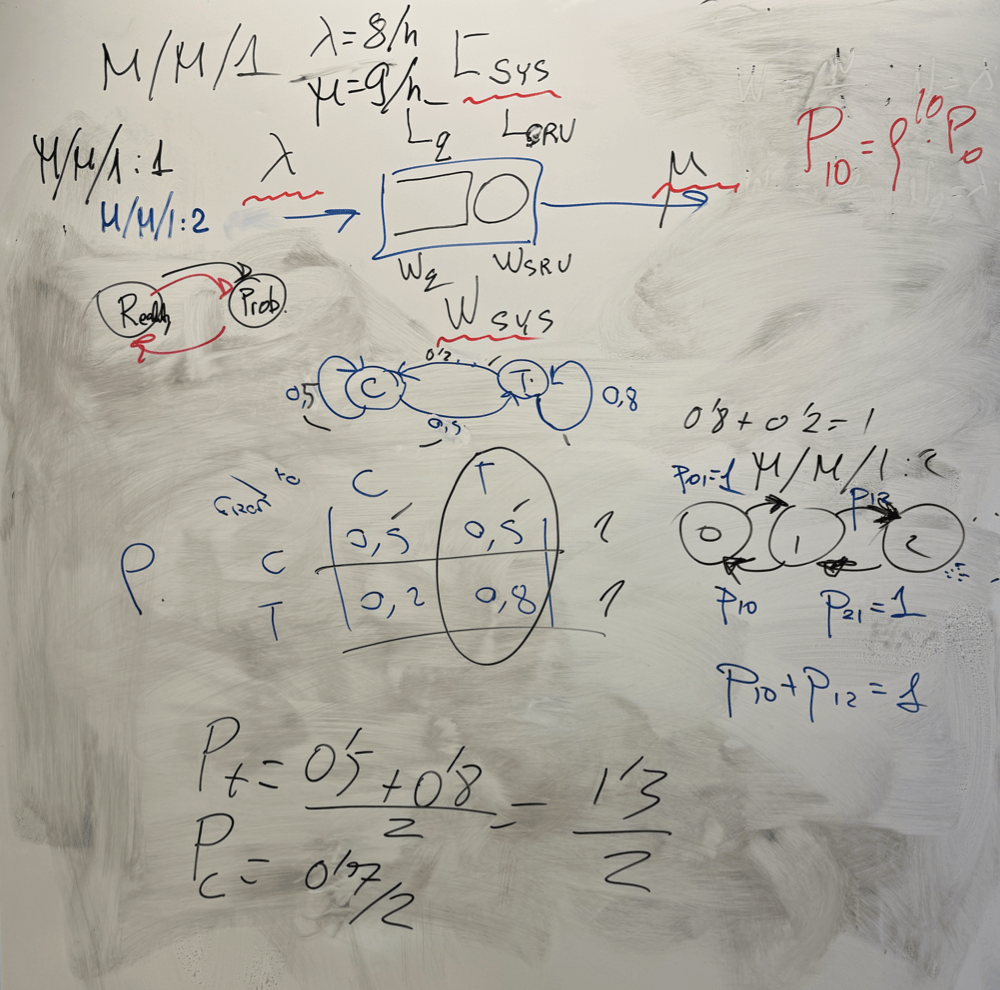
Classwork
Week 6
Week #7
From Observation to Models
2024-03-11
Classwork Time
Week 7
Classwork
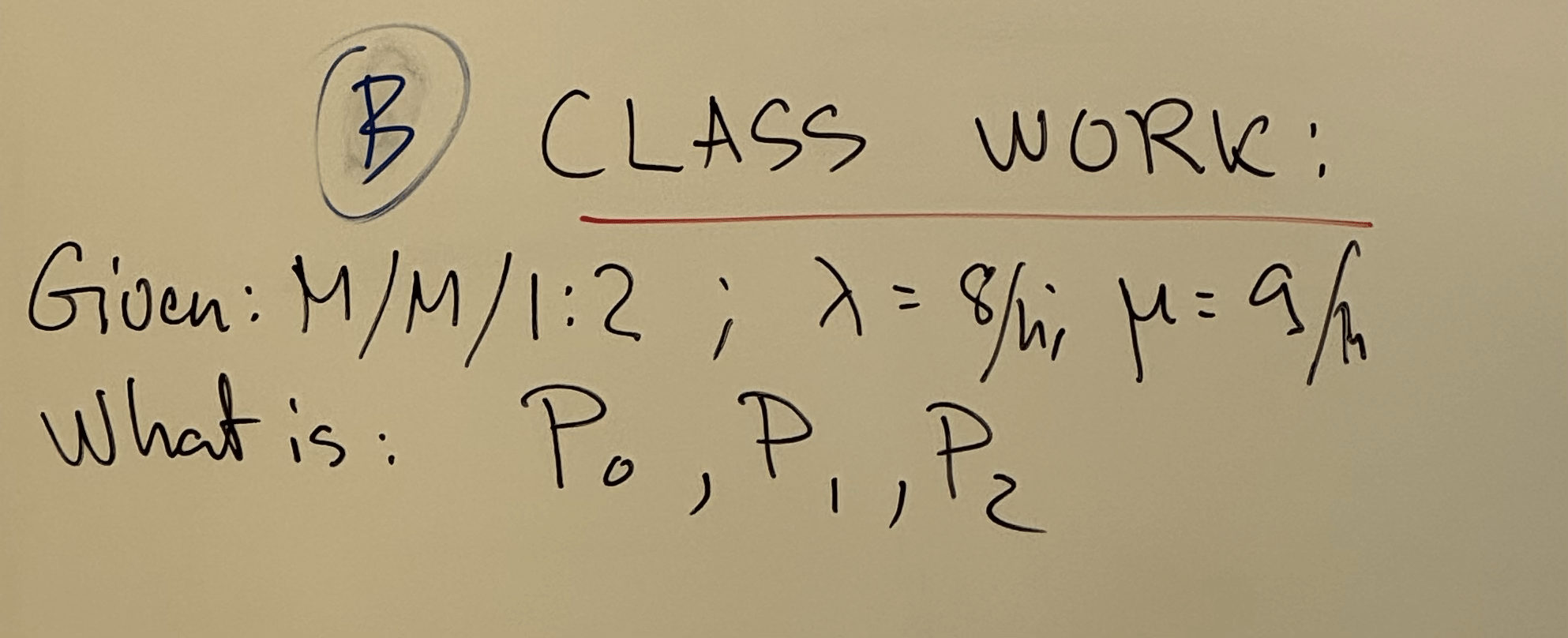
Week 7
Classwork
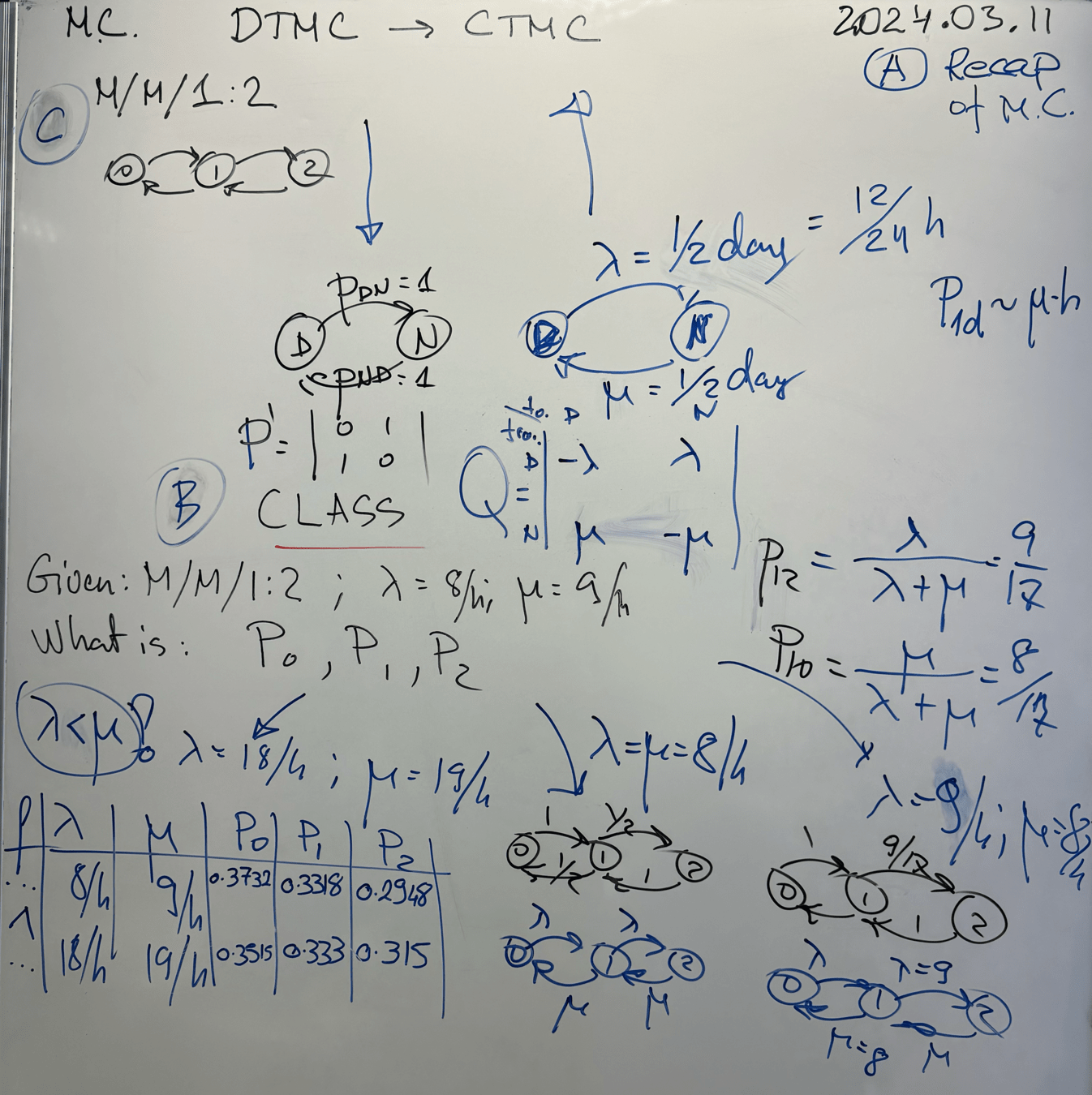
Week 7
Classwork
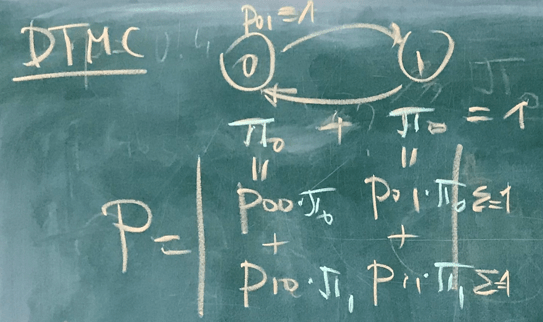
Week 7
Classwork
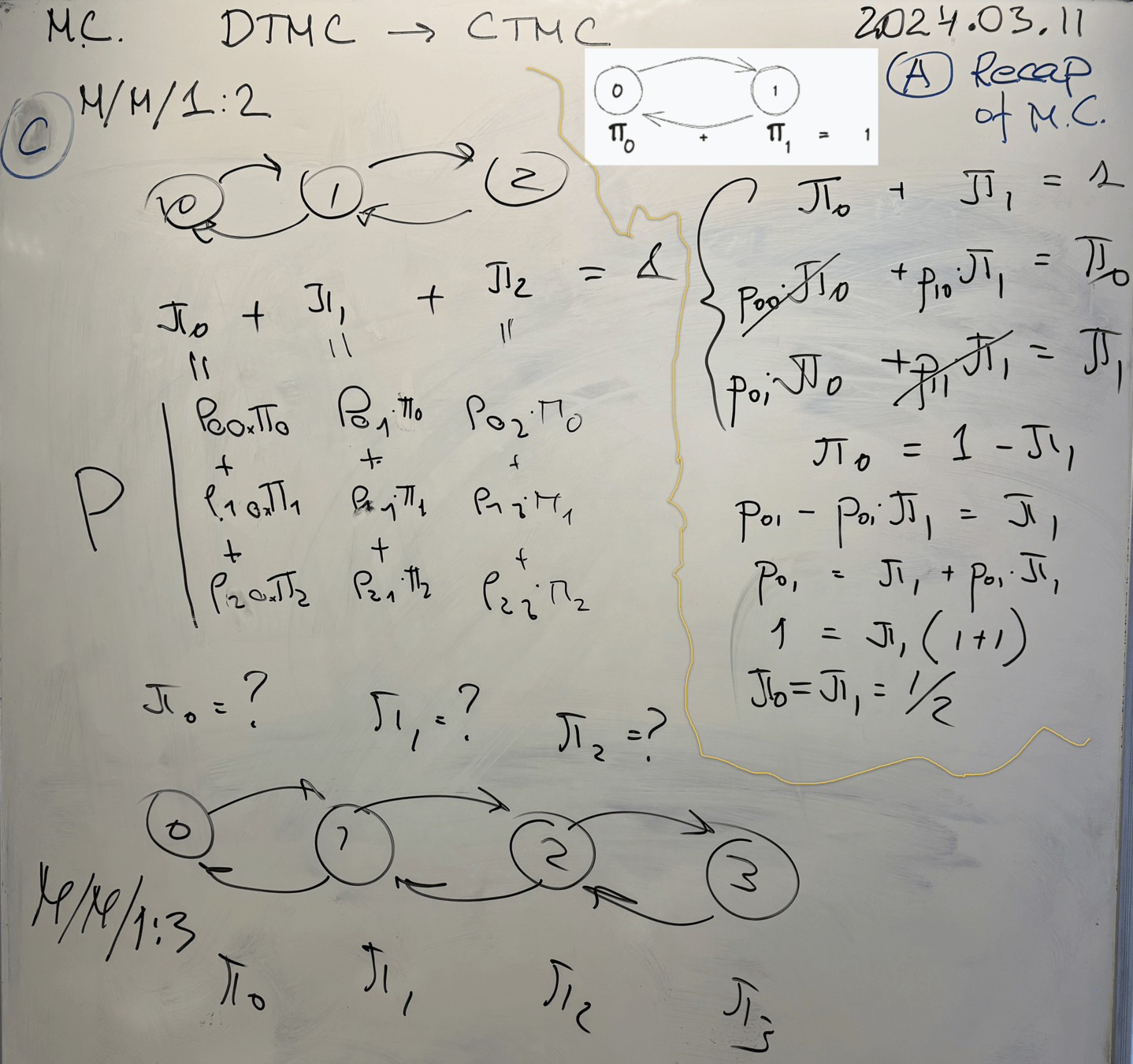
Pre-Class Week 8
Homework - Part 1
Learning Markov Chains
1. Record your voice in AUDIO format, explaining the terms used in the Equation system.
2. Use screen recording to point to the terms you are discussing.
3. Publish your record in the Slack HOMEWORK CHANNEL.
Week #8
Infinite and Finite
2024-03-18
2nd Module Exam
APPROACHING
Theoretical Models
Service Systems
Week #8
From Observation to Models
2024-03-18
https://towardsdatascience.com/sql-joins-a-brief-example-9d015868b56a
https://www.google.com/search?q=andrey+andreyevich+markov&rlz=1C5CHFA_enLV889LV889&sxsrf=APq-WBsyI88xAvtsq7nGDiBEw2fcxhf7gg:1646897947719&tbm=isch&source=iu&ictx=1&vet=1&fir=1mWzaoYlCdvr8M%252Cv3SWMCoFghWAVM%252C%252Fm%252F0kz0%253BfJgqZDzcP0pUaM%252Co_AQCFk0WdmyFM%252C_%253BmBXNaksaj7WQ0M%252C12KOCiPVrIPXPM%252C_%253BmTj0m0tPFcUyKM%252C80KAu9zJ0rx8jM%252C_%253B18svUHl8YhDi9M%252CSgL9fpTCX3B9zM%252C_%253BVplz4lXluhbLiM%252CC613xlUTf5RX7M%252C_%253BElZthqyswocQ-M%252COGOZlLA1jJicWM%252C_%253BWIPpos0yzSuwOM%252C8POXzH7gnQ6F0M%252C_%253BVeyJaCGraCGUDM%252C8POXzH7gnQ6F0M%252C_&usg=AI4_-kR2sk7mcGr3QPtmSzFvW1MvfgN3fA&sa=X&ved=2ahUKEwjp5p35hLv2AhUhR_EDHTAhBhoQ_B16BAgpEAE#imgrc=5hEhbQsA4C8tUM
Week 8
FINITE SYSTEMS
DTMC
(Discrete-Time Markov Chains)
Markov Chains
CTMC
(Continuous-Time Markov Chains)
Challenges
Markov Models
BOOKS
SLIDES
VIDEOS
STACKEXCHANGE
Week 8
FINITE SYSTEMS
DTMC
Markov Chains
CTMC
Week 8
CLASSWORK
DTMC
Learning Markov Chains
OVERVIEW on DTMC
Aperiodic irreducible DTMCs are ergodic since each
has at least one state i with
pi,i>0
p_{i,i} > 0
Demonstration Time
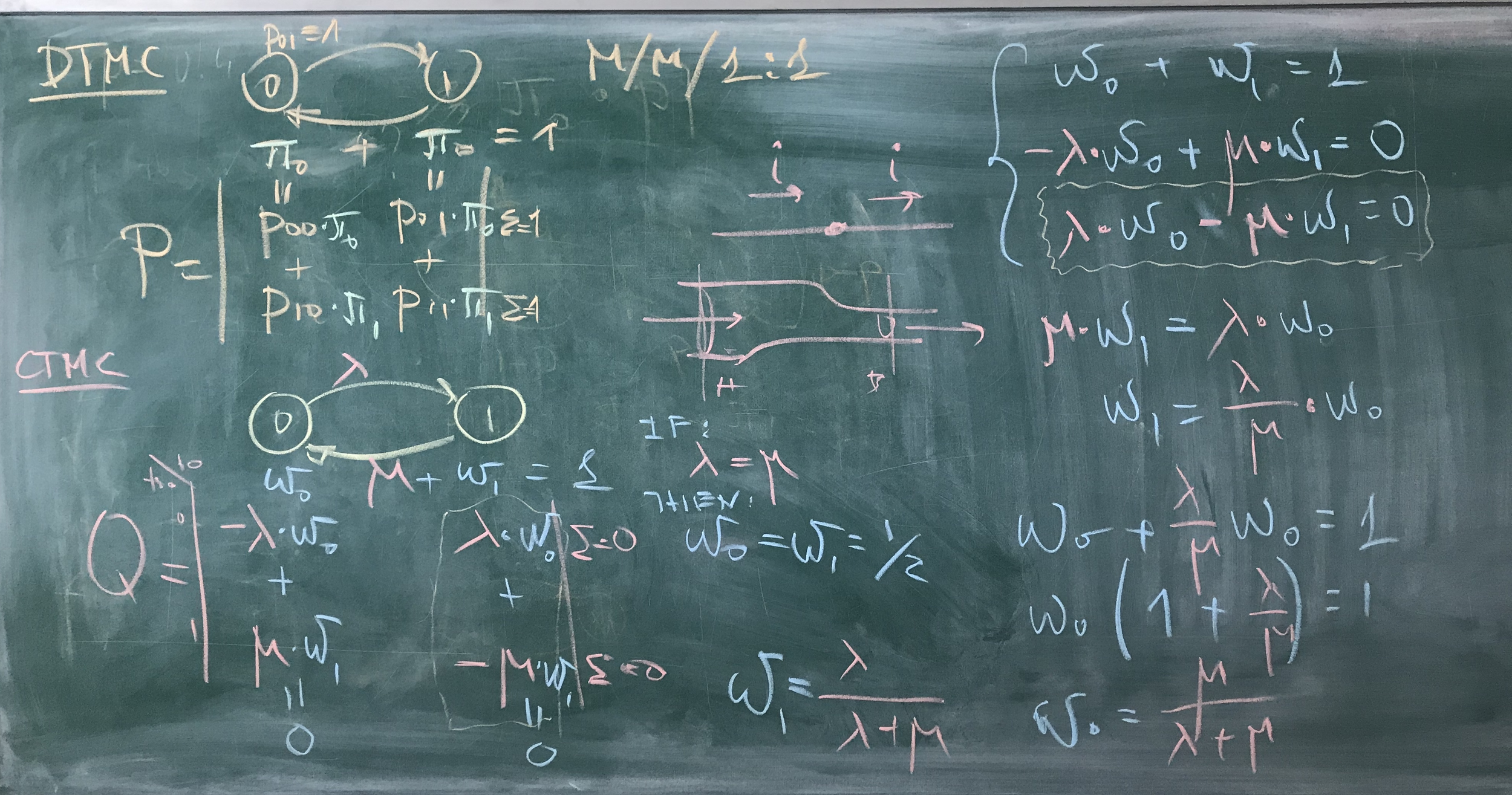
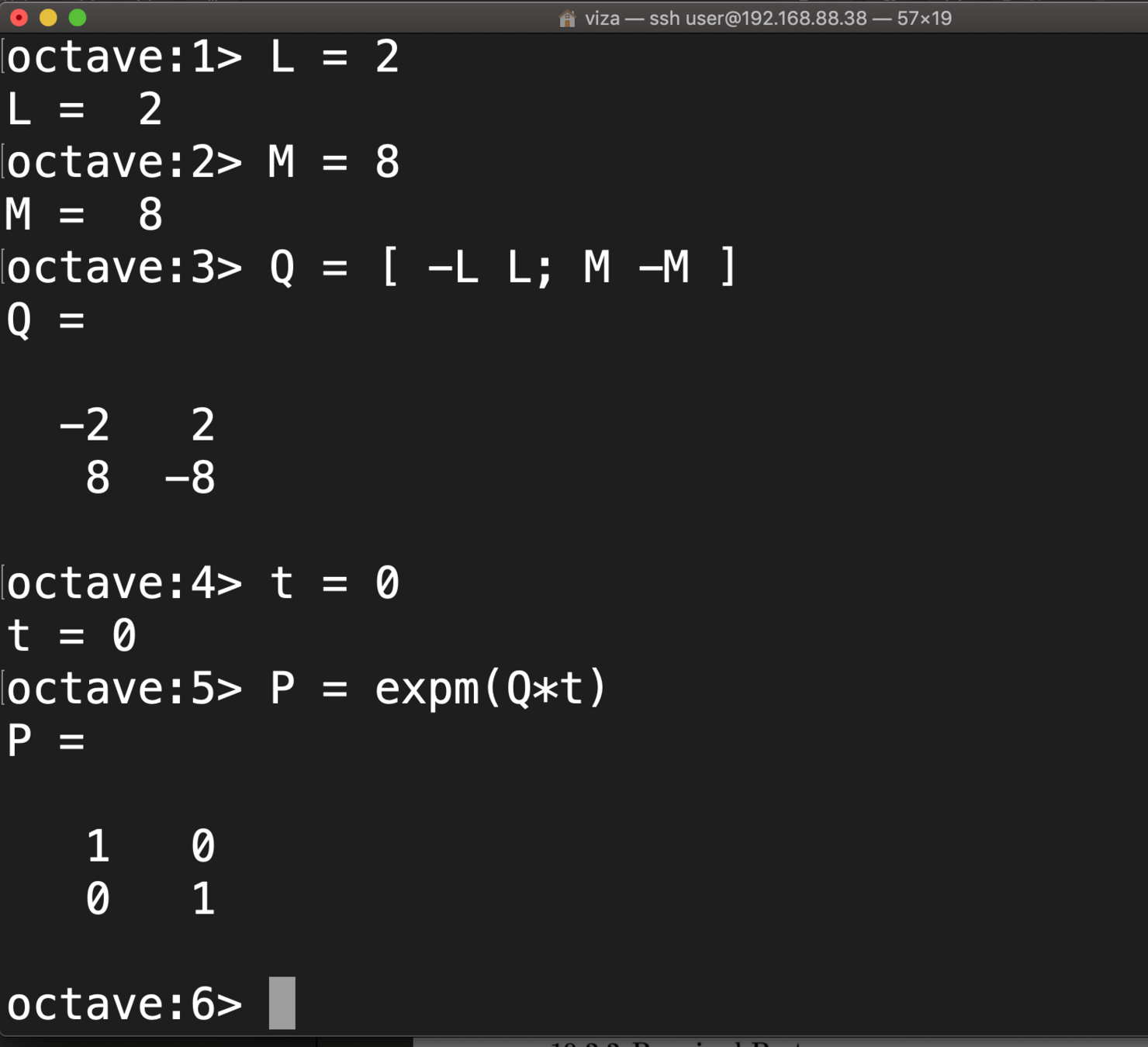
Week 8
DTMC
PROFESSOR-UMBRELLA MODEL
Learning Markov Chains
Classwork
Week 8
Classwork
Week 8
DTMC
Learning Markov Chains
- PROFESSOR has 2 UMBRELLAS
- For example, there is a chance of rain with one umbrella available at home, but even if the rain does, and the professor takes the umbrella to work, he/she will take it back if the precipitation occurs again. One can't take more than one umbrella, so the number of umbrellas varies from walk to walk AND from the weather conditions. But, if there is no rain occurring outdoors, the professor can forget to take an umbrella, like every one of us usually does. So, in the situation, if NO umbrellas are available, the bad (wet) things happen - you can easily guess what.
- Compute and sketch the function of the probability of "getting clothes sodden" in a long term process (let's say - 60 walks) depending on the rain probability
P(gettingwet)=f(P(rain))
P(getting\> wet) = f(P(rain))
P(rain)
P(rain)
Classwork
Week #9
From Observation to Models
2024-04-08
F.A.S.T.
https://medium.com/big-self-society/jim-kwiks-fast-method-will-help-you-learn-faster-5d3d669dc3b5
method
Week 9
Moving towards Reality
Homework - Part I and II
Learning through Models
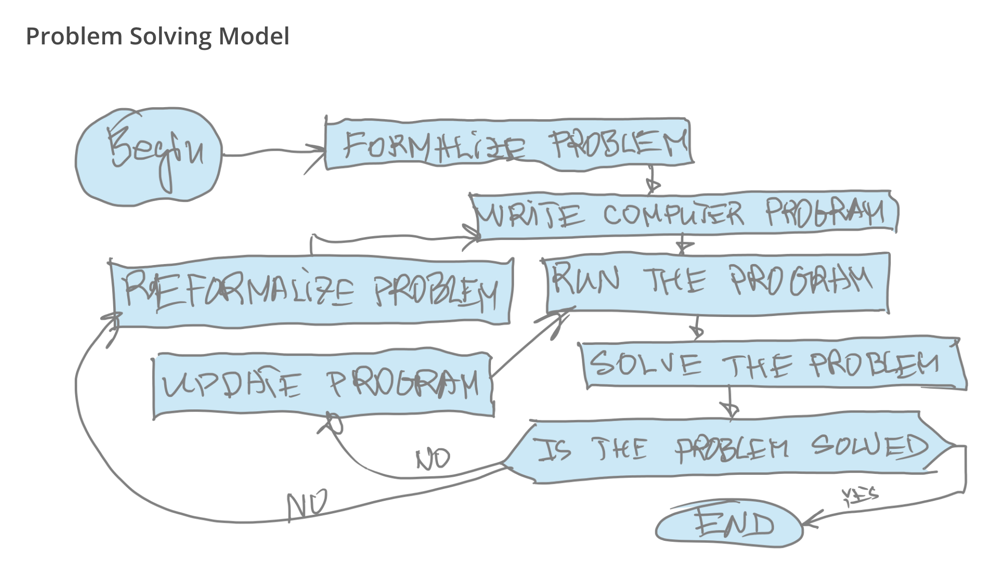
Where is the Key of Problem Solving?
quantitative-model-checking
Week 9
FINITE SYSTEMS
DTMC
(Discrete-Time Markov Chains)
Markov Chains
CTMC
(Continuous-Time Markov Chains)
quantitative-model-checking
Demonstration Time
CTMC
(Continuous-Time Markov Chains)
Quantitative Model Checking
Week 9
Homework - Part I
CTMC
Learning Markov Chains
- BARBER-SHOP
- has 2 SEATS and 2 EXTRA WAITING SEATS
- Two BarBERS are operating
- If, ...
P(OneExtraSeatWillBeBusyAfter2HoursOfOperating)=?⋅
P(OneExtraSeatWillBeBusyAfter2HoursOfOperating) = \> ? \> \cdot
https://www.coursera.org/learn/quantitative-model-checking/lecture/DWlJz/definition-of-a-ctmc
quantitative-model-checking
Week 9
Homework - Part II
Demonstrate progress in the course:
https://www.coursera.org/learn/quantitative-model-checking/lecture/DWlJz/definition-of-a-ctmc
quantitative-model-checking
Week #10
From Observations to Models
2024-04-15
to PN
From
Week 9
Homework
Submit Matlab/Octave
code and plots related to BarberShop problem
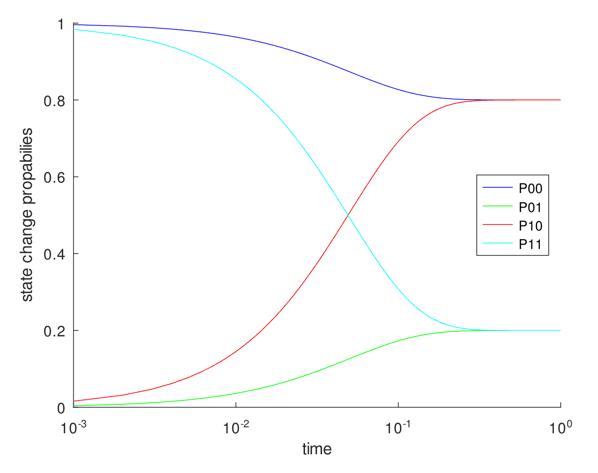
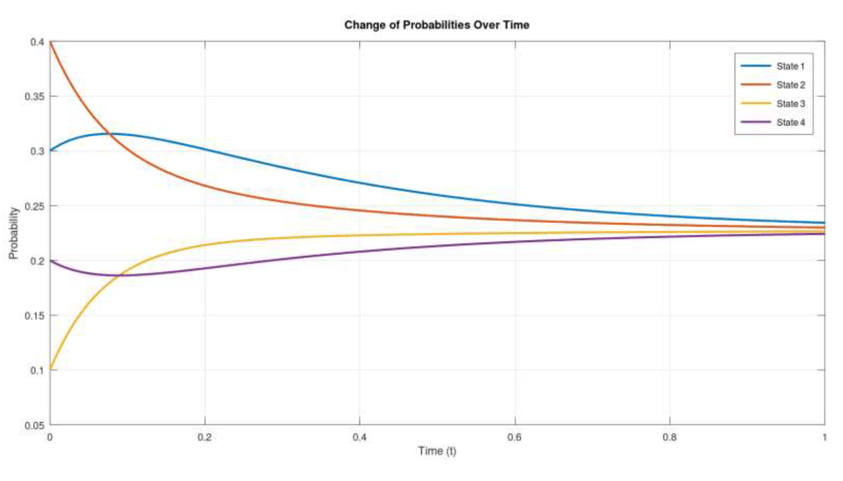
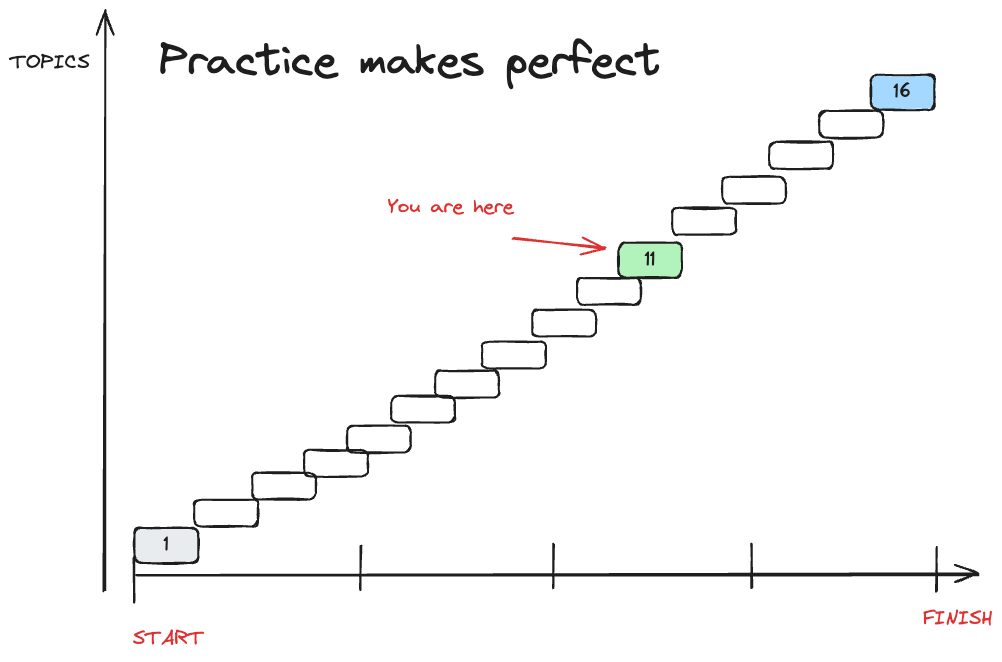
Week 10
Homework - Part I
Get and Install the Snoopy tool
from Cottbus Uni
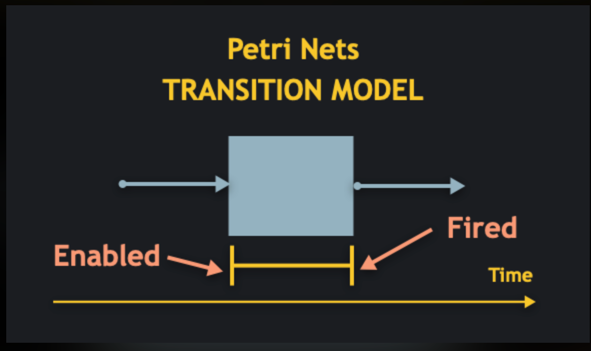
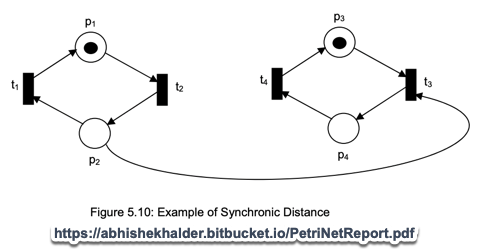
Learning Petri Nets
Demonstration Time
PN
(Petri Nets)
0
1
0
1
MarkovChain
Petri Net
Control Element
State
State
Place
Place
Transition
Transition
State Index
Number of
Tokens
Week 10
Homework - Part II
Using Snoopy
Learning Petri Nets
Transforming MC models
(e.g. BarberShop)
into simple but stochastic Petri Nets
Week #11
From Observations to Models
2024-04-15
to
From
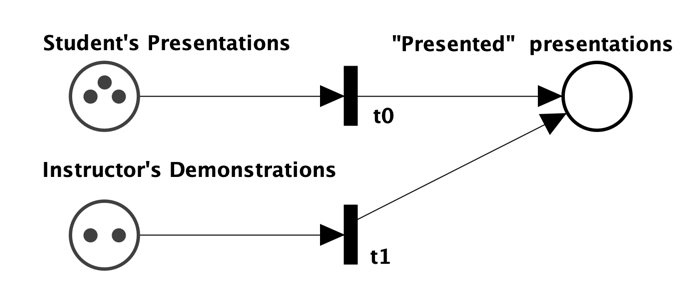
Week 11
Moving towards Reality
Including all Homework Fragments
Demonstration Time
Tokens are on the Students' Court
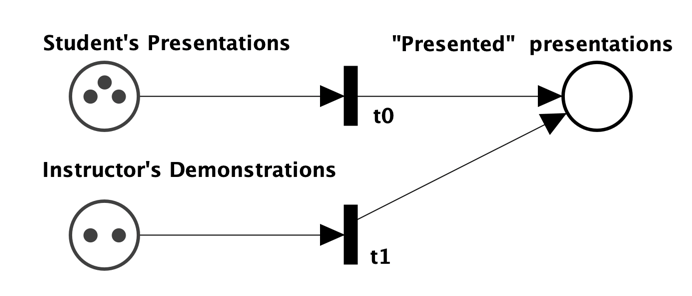
Demonstration Time
The token is on the Instructor's Court
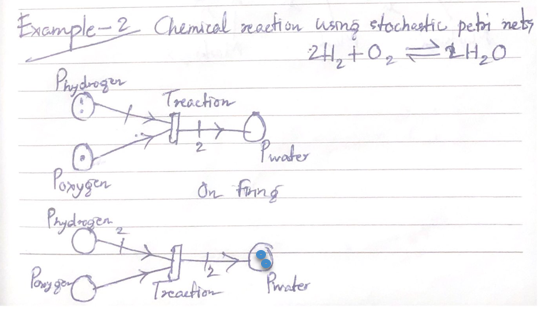
Week 11
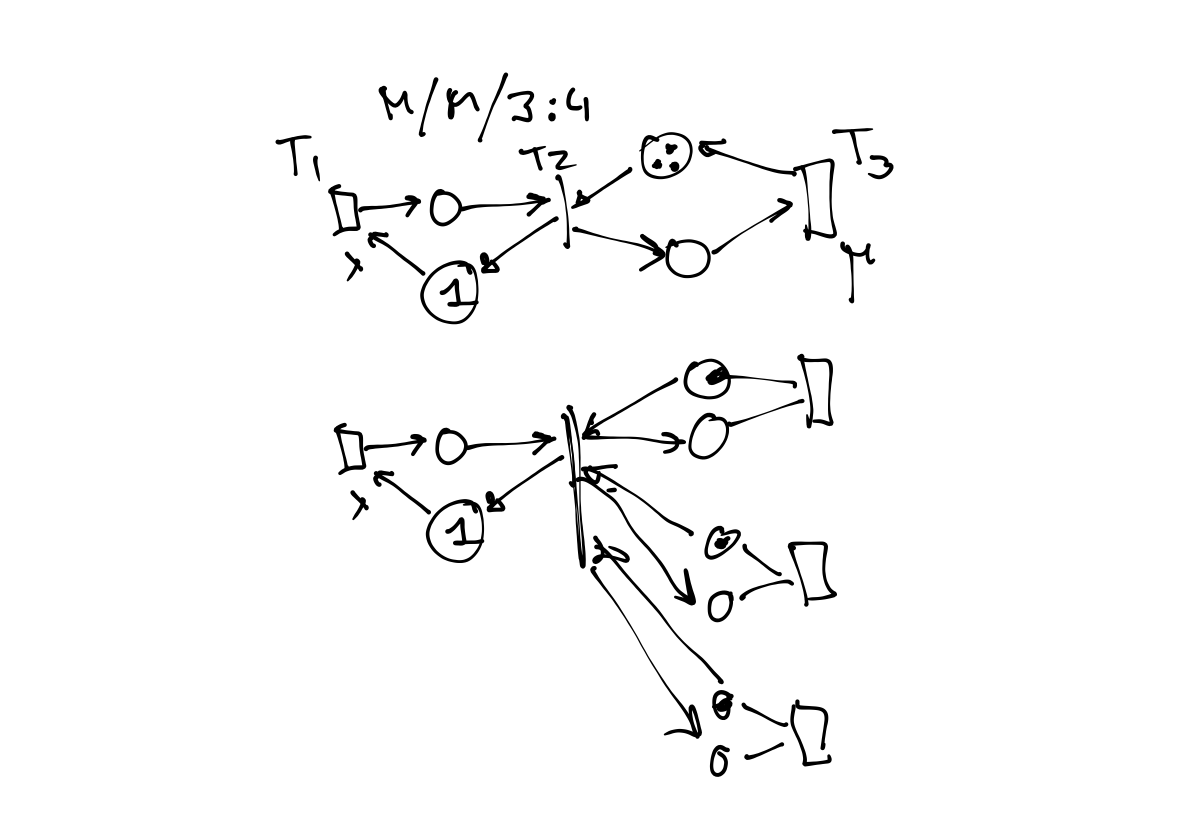
Homework - Part I
Learning Petri Nets
Output
- Demonstrate understanding of the topic, and namely,
- Publish a handwritten recap of the lecture examples {Ex.1 .. Ex. 6} with comments
Participate in DELHI UNI Lecture:
Mod-05 Lec-08 Stochastic Petri Nets
Week 11
Homework - Part II
Using Snoopy Tool and STPN Model,
Learning Petri Nets
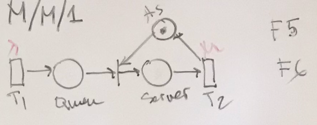
Verify an Algebraic Model for the System M/M/1
through Load and Waiting Time metrics
Output
- On YouTube published Video Report
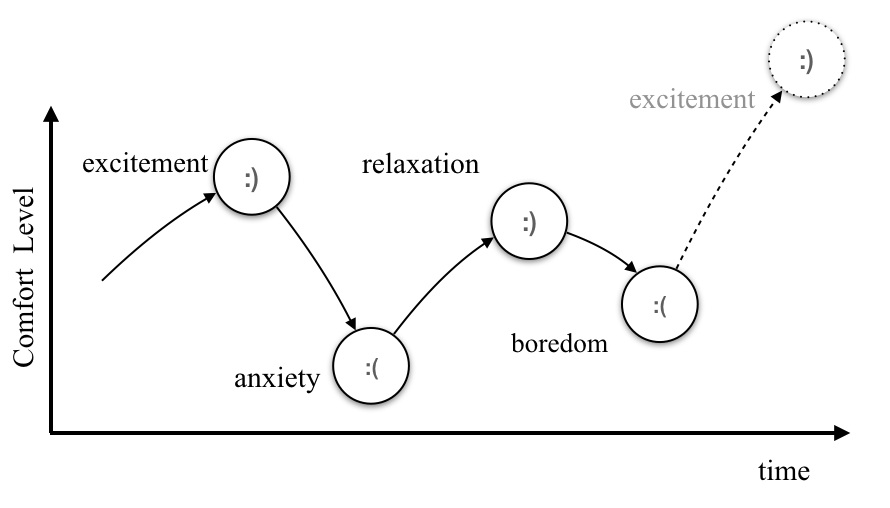
Emotional Cycles
Week 1
Week 2
...
Week13
.END
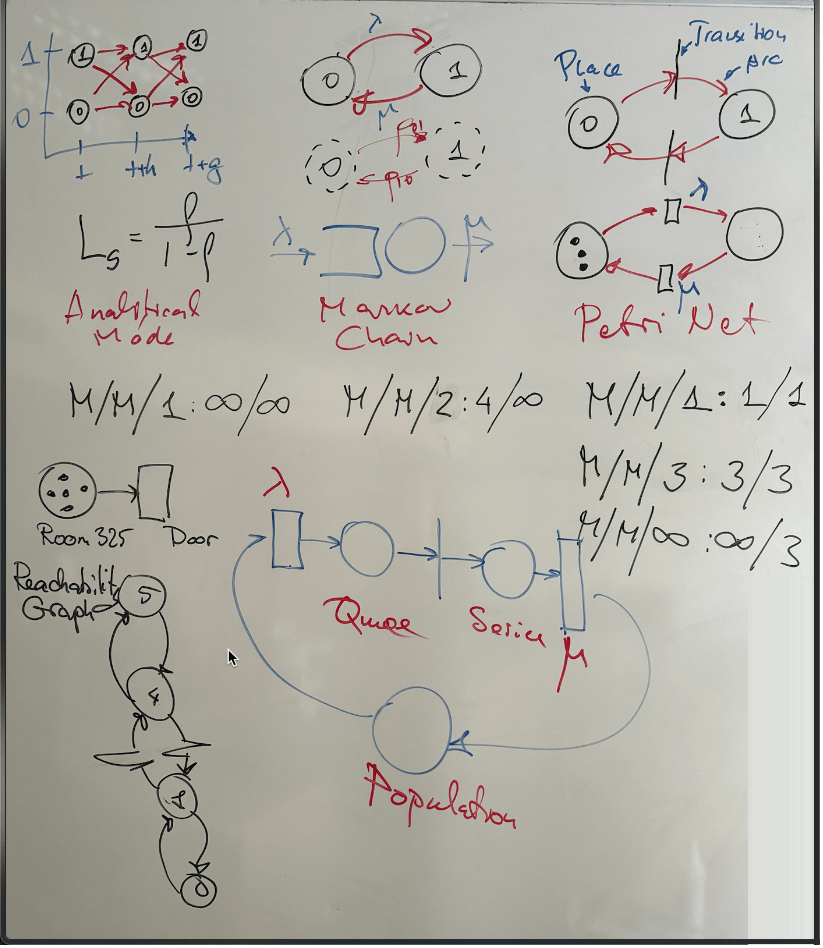
CLASS NOTES
Week #12
From Observations to Models
2024-04-22
to
From
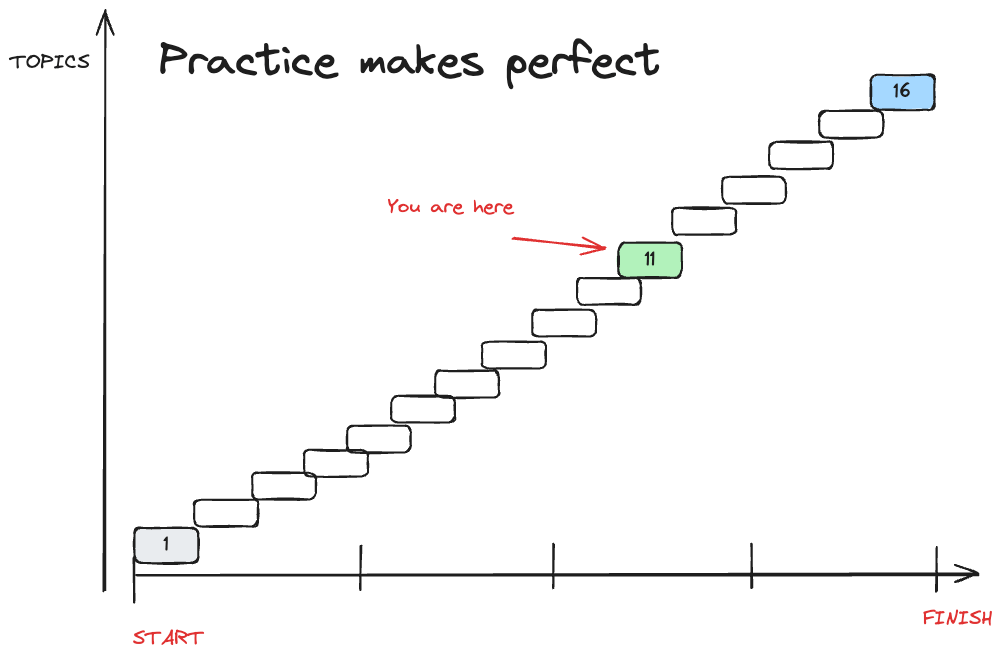
a SEMI-ULTIMATE Tool
Petri Nets in Modelling
Week 12
TODO: start thinking about the model
BW = 10 Mbps
BW = 100 Mbps
BW = 100 Mbps
queue size?
Tdatatransfer=f(V,BW1,BW2,BW3,λ,N)
T_{data\> transfer} = f(V, BW_1, BW_2, BW_3, \lambda, N )
Volume = {1..10} // Integer [Byte/Packet/Message]
Priority = {Low, High} // Integer
Origin = {1, 2} // Integer
Destination = {1 .. 6} // Integer
iat = { 12 .. } // Double [1/min]
lambda = { 5 .. } // Double [1/hr]
minQueueLength = {0...N}; // Integer
Server
Client 2
Client 1
Controller
Synchronous
Asynchronous
BWk=1,10,10,1000,…bps,Kbps,Mbps,…
BW_k = {1,10,10,1000, \ldots} \> bps, Kbps, Mbps, \ldots
BW1=100bps
BW_1 = 100 \> bps
BW2=10bps
BW_2 = 10 \> bps
BW3=1bps
BW_3 = 1 \> bps
Asynchronous
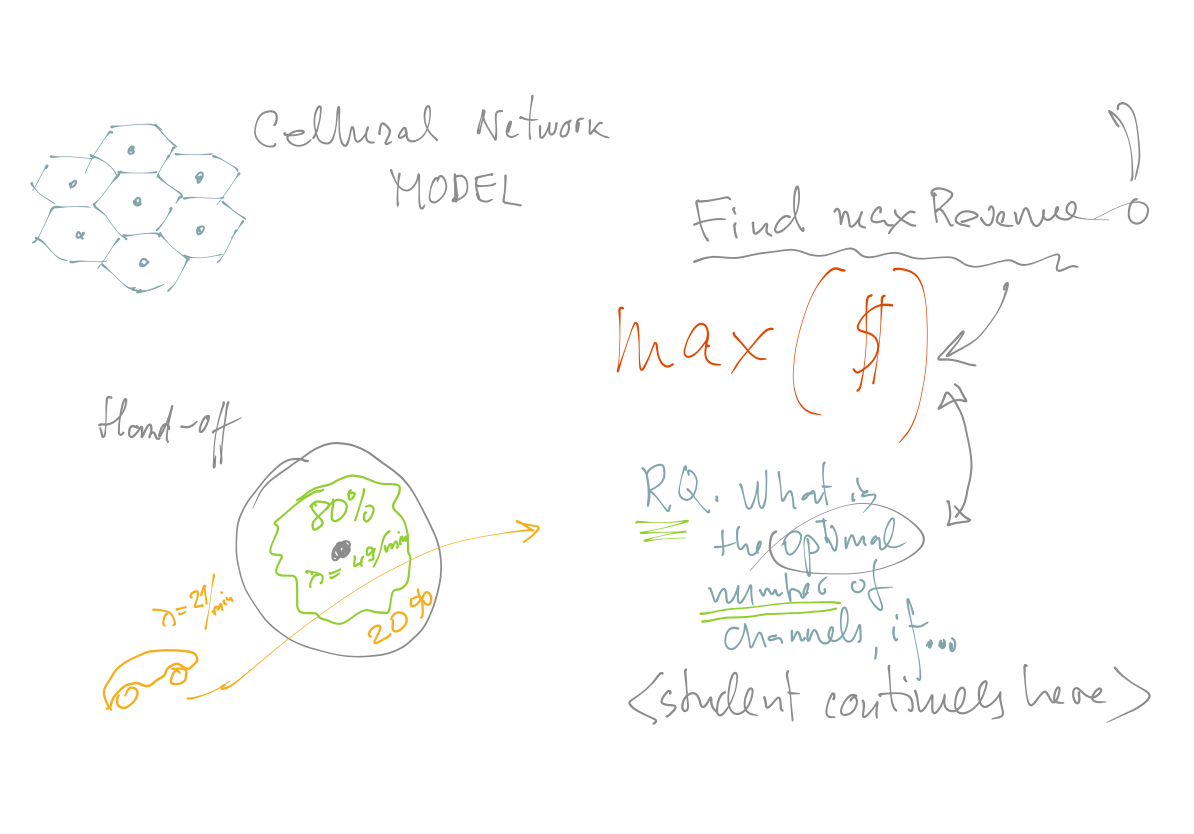
Engineering Question: What is a value of
Scientific Research Topics
- e.g. "Verifying theoretical M/M/x:x/x/x models utilising Petri Nets".
- How to make queues, protocols and services better?
- e-mails, notifications, chats, bots, scheduling systems and apps
- authentication, authorisation, etc. protocols
- networking software/hardware, PLC controllers, etc.
- Modelling with Higher-Order Tools
- PRISM Model Checker (from OXFORD UNI),
- UUPAAL
- ns-3,
- Fuzzy Logic Systems,
- ...
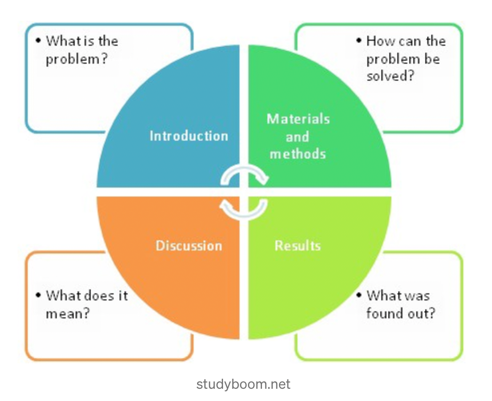
https://medium.com/literacy-discourse/what-does-imrad-reveal-about-science-7de7741ba987
Use IMRAD to demonstrate
Research Results
https://medium.com/literacy-discourse/what-does-imrad-reveal-about-science-7de7741ba987
Use IMRAD to demonstrate
Research Results
“Results are where the findings and the outcomes go.”
Week #13
From Observations to
Approved Models
2024-04-29
AND
VERIFIED BY
MODEL
CHECKER
MODEL
CHECKER
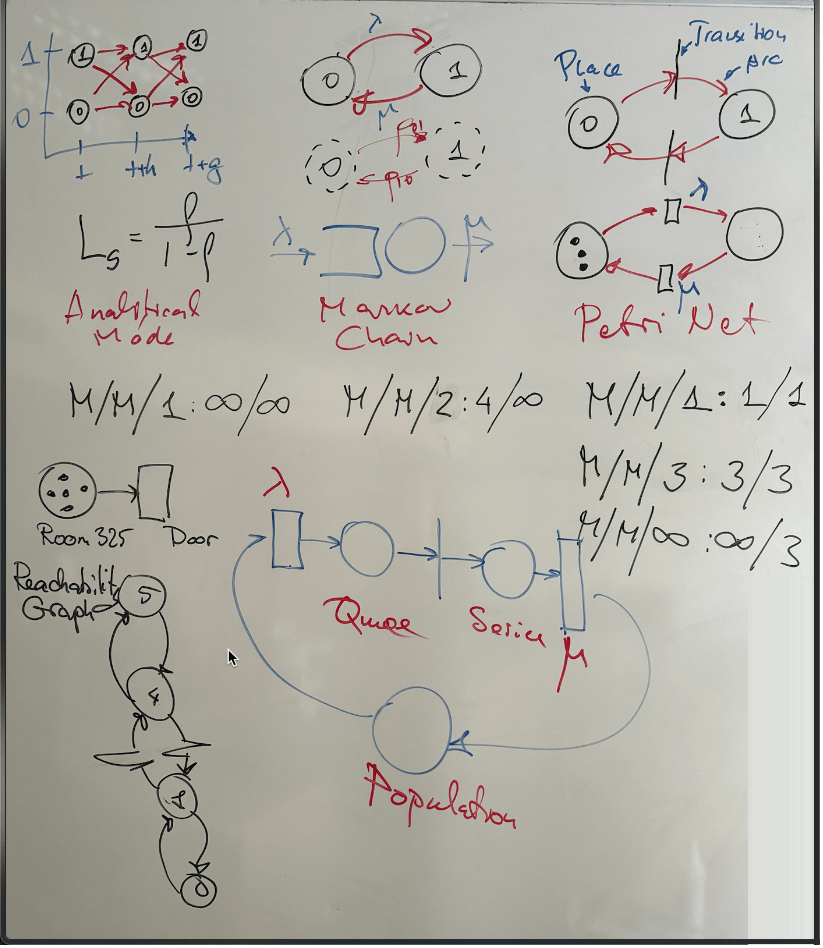
CLASS NOTES
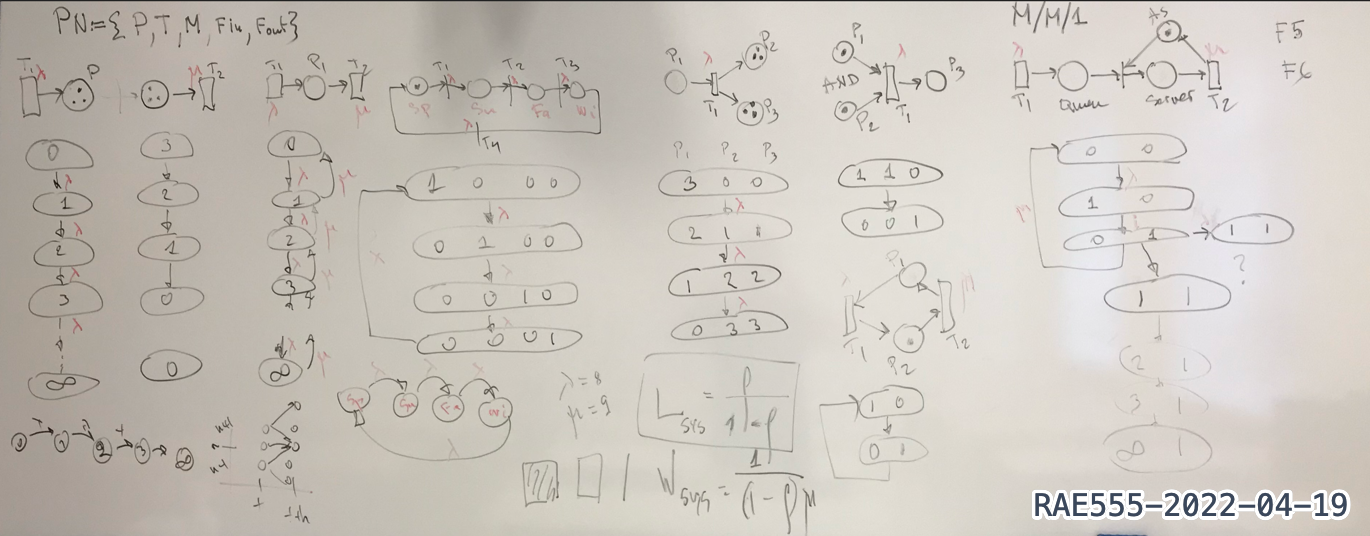
The problem
The problem
The problem
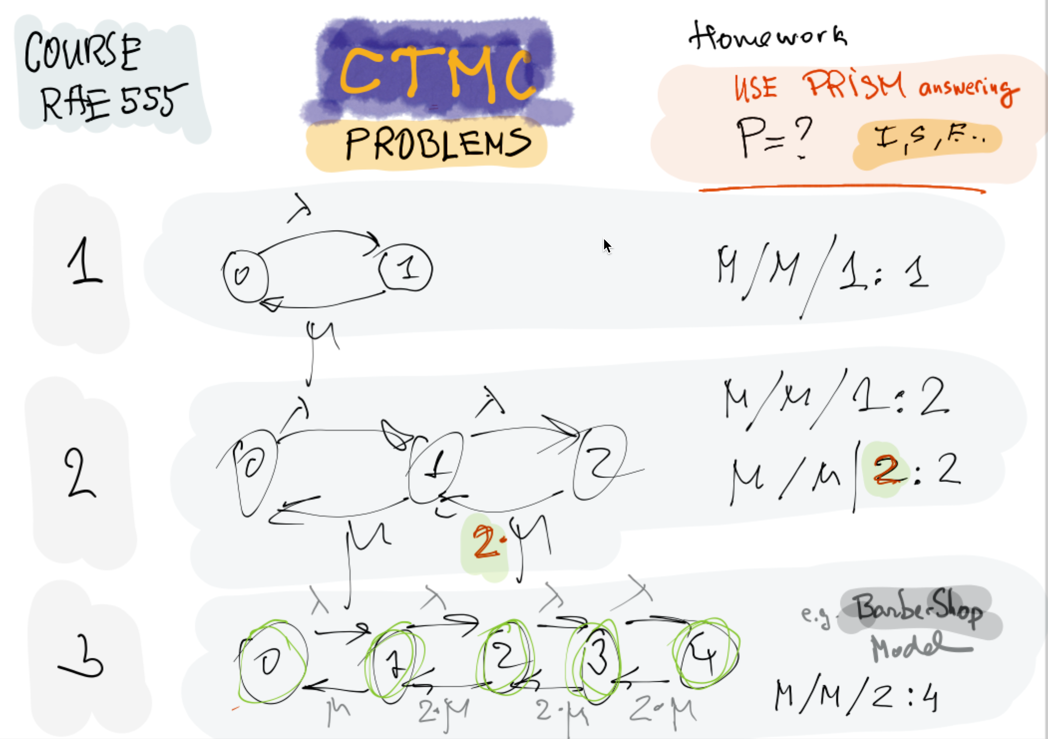
https://www.prismmodelchecker.org/
The problem
THE PROBLEM
Week 13
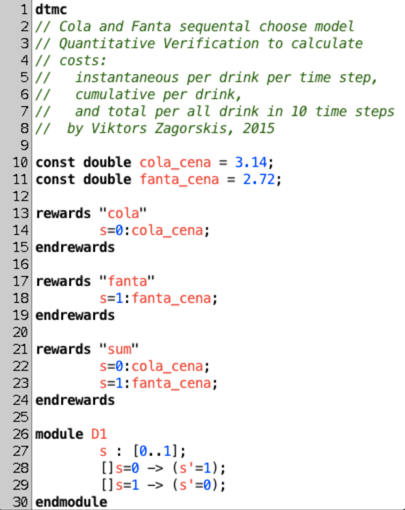
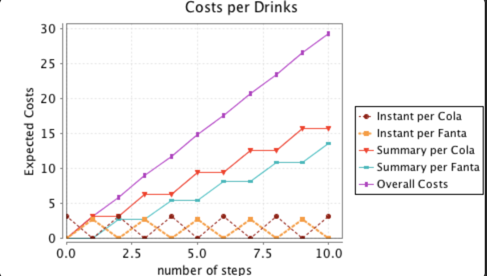
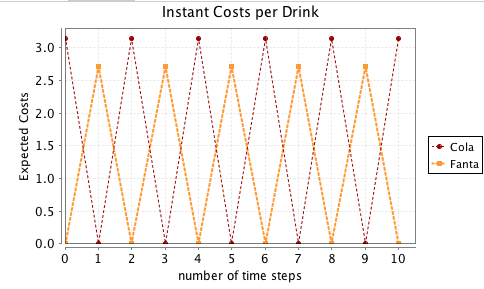
Week 13
Homework
using
PRISM MODEL CHECKER
Verifying Markov Chains
BARBER SHOP MODEL
Week #14
From Observations to
Reliable Models
2024-xx-xx
AND
VERIFIED BY
MODEL
CHECKER
From Observations to
Reliable Models
https://youtu.be/H6vSIM754X4
https://youtu.be/H6vSIM754X4
-
Focus
-
Fundamentals
-
Structure
That kick required is ...
PRACTICE
Demonstration Time
The token is on the Students' Court
Demonstration Time
The token is on the Students' Court
The problem
Demonstration Time
The token is on the Students' Court
Demonstration Time
The token is on the Students' Court
https://www.prismmodelchecker.org/
TODO
Initiate Your Research
Week 16
TODO (PRE-CLASS)
Do research like masters do!
Week 16
TODO (PRE-CLASS)
T=f(V,BW1,BW2,BW3,λ,N)
T = f(V, BW_1, BW_2, BW_3, \lambda, N )
Volume = {1..10} // Integer [Byte]
Priority = {1 .. 3} // Integer
Origin = {1.. 2} // Integer
Destination = {1 .. 6} // Integer
iat = { 12 .. } // Double [1/min]
lambda = { 5 .. } // Double [1/hr]
Integer minQueueLength = {0...N}; N_max = 1000
Server
Client 2
Client 1
Controller
Synchronous
Asynchronous
BWk=1,10,10,1000,…bps,Kbps,Mbps,…
BW_k = {1,10,10,1000, \ldots} \> bps, Kbps, Mbps, \ldots
BW1=100bps
BW_1 = 100 \> bps
BW2=10bps
BW_2 = 10 \> bps
BW3=1bps
BW_3 = 1 \> bps
Asynchronous
- Studying principles of Traffic Models in Packet-based Network
- Mapping real network observations to empirical Theoretical Models
https://arxiv.org/pdf/1105.1347.pdf
T=f(V)
T = f(V)
http://www0.cs.ucl.ac.uk/staff/m.handley/slides/nnfn-tcp.pdf
Week 16
TODO (PRE-CLASS)
Demonstration Time
The token is on the Instructor's Court
- Studying principles of Traffic Models in Packet-based Network
- Mapping real network observations to empirical Theoretical Models
Experiments with TCP flow finding an approximating function representing a waiting time for varying amount of data;
e.g. 1KB ... 100MB transferred from Server Instance to Client using 100 Mbps link on local PC machine.
Repeat the experiment, utilizing UDP protocol with up to 8 simultaneous flows.
Prepare video report providing relevant experiment objectives, describing experiment, and presenting code, diagrams, and outcome discussion.
Week 16
TODO (PRE-CLASS)
- Studying principles of Traffic Models in Packet-based Network
- Mapping real network observations to empirical Theoretical Models
Week 16
TODO (PRE-CLASS)
- Studying principles of Traffic Models in Packet-based Network
- Mapping real network observations to empirical Theoretical Models
Week 16
TODO (PRE-CLASS)
- Studying principles of Traffic Models in Packet-based Network
- Mapping real network observations to empirical Theoretical Models
Week 16
TODO (PRE-CLASS)
T=f(V,BW1,BW2,BW3,λ,N)
T = f(V, BW_1, BW_2, BW_3, \lambda, N )
Volume = {1..10} // Integer [Byte]
Priority = {1 .. 3} // Integer
Origin = {1.. 2} // Integer
Destination = {1 .. 6} // Integer
iat = { 12 .. } // Double [1/min]
lambda = { 5 .. } // Double [1/hr]
Integer minQueueLength = {0...N}; N_max = 1000
Server
Client 2
Client 1
Controller
Synchronous
Asynchronous
BWk=1,10,10,1000,…bps,Kbps,Mbps,…
BW_k = {1,10,10,1000, \ldots} \> bps, Kbps, Mbps, \ldots
BW1=100bps
BW_1 = 100 \> bps
BW2=10bps
BW_2 = 10 \> bps
BW3=1bps
BW_3 = 1 \> bps
Asynchronous
Week 16
TODO (PRE-CLASS)
T=f(V,BW1,BW2,BW3,λ,N)
T = f(V, BW_1, BW_2, BW_3, \lambda, N )
Volume = {1..10} // int [Byte]
Priority = {1 .. 3} // int
Origin = {1.. 6} // int
Destination = {1 .. 6} // int
iat = { 12 .. } // Double [1/min]
lambda = { 5 .. } // Double [1/hr]
BW = 1 bps
BW = 100 bps
BW = 100 bps
int minQueueLength = 0;
Week 16
TODO (PRE-CLASS)
BW = 10 Mbps
BW = 100 Mbps
BW = 100 Mbps
queue size?
ns-3
Week 16
TODO (PRE-CLASS)
queue size?
REAL NETWORK
Week 16
TODO (PRE-CLASS)
TODO
Week 16
TODO (PRE-CLASS)
Reflection on another Research
Week #15
From Passive Observation
to Wise Action
2024-05-13
F.A.S.T.
with
F.A.S.T.
do Forget
be Active
find the State
Teach the others
Jim Kwik
EXAM
time
It's about
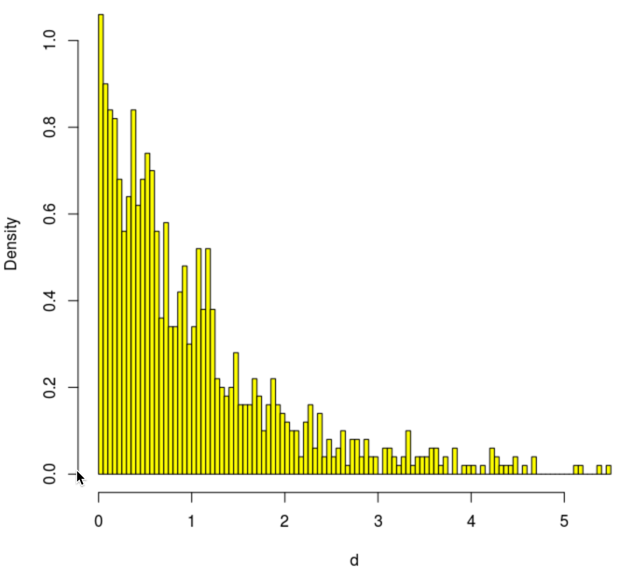
Week 15
Homework - part I
with
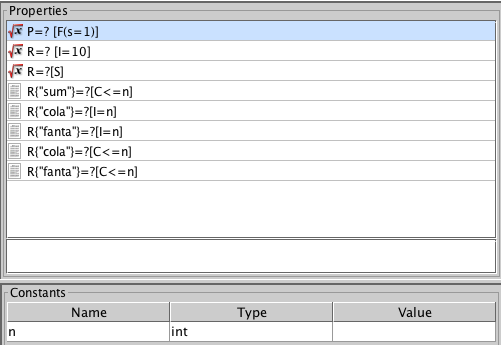
PRISM MODEL CHECKER
Verifying
ANY
Queueing Model
Week 15
Homework - part II
with
Rabbit-MQ
Running, Validating and Verifying
ANY
Queueing Model
That kick required to become FAST is ...
PRACTICE
PRACTICE PARADIGM
What is Rabbit-MQ ?
https://www.rabbitmq.com/
One broker to queue them all
What is Rabbit-MQ ?
https://www.rabbitmq.com/
One broker to queue them all
RabbitMQ is a reliable and mature messaging and streaming broker, which is easy to deploy on cloud environments, on-premises, and on your local machine. It is currently used by millions worldwide.
Simplest BROKER
WORK QUEUES
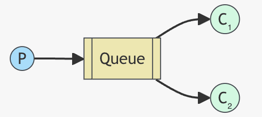
Competing Consumers pattern
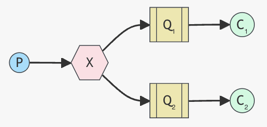
WORK QUEUES
Publish/Subscribe pattern
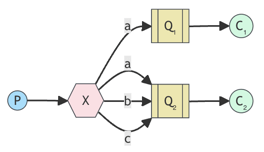
ROUTING
Receiving messages selectively
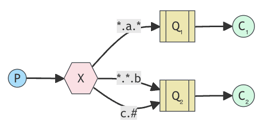
TOPICS
Receiving messages based on a pattern (topics)
RPC
Request/Reply pattern
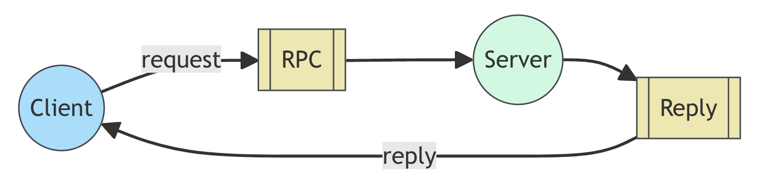
RPC
Request/Reply pattern
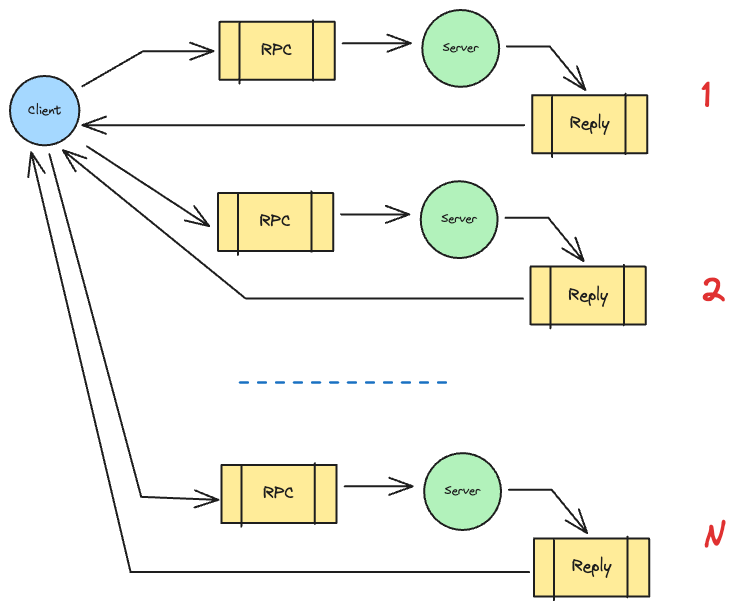
Week 15
Homework - part II
with Rabbit-MQ
Running, Validating and Verifying
ANY
Queueing Model
It's time to demonstrate your skills and competence in
PRACTICE
RABBIT MQ
EXAM TIME
Week 16
EXAM TIME
Week 17
EXAM TIME
Week 17
"What did you learn in RAE 555?"
The course staff would love to hear about what you learned this semester.
What were some highlights?
It would be best to publish your story and all personal materials produced during the course on a static WEB site on
VERCEL or NETLIFY.
End of EXAM TIME
Week 18
FINISH
Riga Technical University
Course 555 Spring 2024
By HPC RTU LV
Course 555 Spring 2024
- 243
