(Vícenásobná) lineární regrese
(Multiple) Linear Regression
Vít Gabrhel
vit.gabrhel@mail.muni.cz
vit.gabrhel@cdv.cz
FSS MU,
14. 10. 2015


Harmonogram
1. Historie
2. Teorie
3. Předpoklady použití
4. Diagnostika
5. Dummy coding
6. Vkládání prediktorů
7. Reportování výsledků
1. O původu lineární regrese I.


1. O původu lineární regrese II.
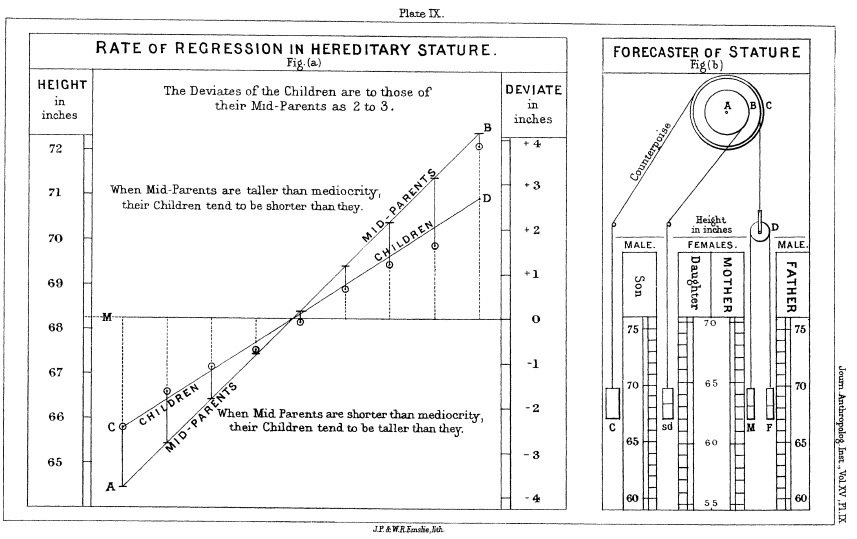
1. O původu lineární regrese III.
Jak to, že děti vysokých rodičů samy bývají vysoké, ale ne tak jako jejich rodiče?
Jak to, že děti útlých rodičů samy bývají útlé, ale ne tak útlé jako jejich rodiče?
Jak to, že nejlepší atlet minulé sezóny letos podává o něco horší výkon než loni?
Regrese k průměru (Regression towards mediocrity)
"It appeared from these experiments that the offspring did not tend to resemble their parent seeds in size, but to be always more mediocre than they-to be smaller than the parents, if the parents were large; to be larger than the parents, if the parents were very small."
"The point of convergence was considerably below the average size of the seeds contained in the large bagful I bought at a nursery garden, out of which I selected those that were sown, and I had some reason to believe that the size of the seed towards which the produce converged was similar to that of an average seed taken out of beds of self-planted specimens."
Galton, 1886, s. 246
1. O původu lineární regrese IV.
2. K čemu slouží lineární regrese?
Lineární regrese
-
Nakolik lze z IQ skóru usuzovat o výkonu v matematice?
- Predikce
Vícenásobná lineární regrese
-
Přispívá k výši platu kromě úrovně vzdělání také pohlaví?
-
Predikce
-
Inkrementální validita
-
Statistická kontrola
-
2. Notace
Y = Y' + e
Lineární regrese
Y' = a + bX
Y' = b0 + b1X1
Vícenásobná lineární regrese
Y' = a + bnXn
Y' = b0 + b1X1 + b2X2 + ... + bnXn + e
Y = Predikovaná (= závislá; outcome) proměnná
Y' = Náš model
e = Chyba měření
a nebo b0 = průsečík (= intercept)
b nebo b1...n = směrnice (= slope)
X1...n = Prediktor (= nezávislá proměnná; predictor)
2. Grafické znázornění
Y = Y' + e
Y' = a + bX
Y' = b0 + b1X1
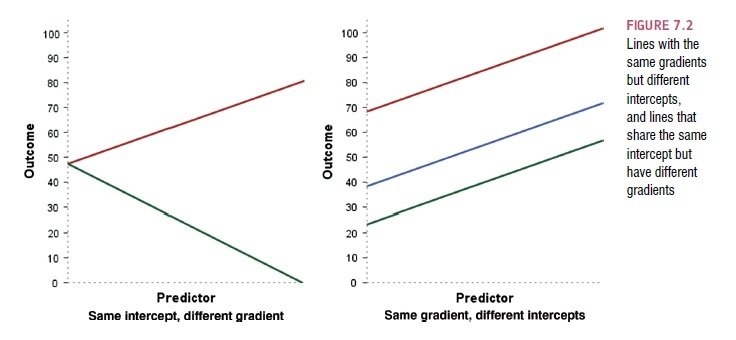
dle Field, 2009, s. 199
2a. Příklad
Skupina pracovníků v podniku BD Technologies si stěžuje vedení firmy, že se roky, které odpracovali ve firmě (X) nepromítají do výše jejich mzdy (Y). Psycholog pracující v tomtéž podniku dostane za úkol zjistit, zda je stížnost pracovníků oprávněná.
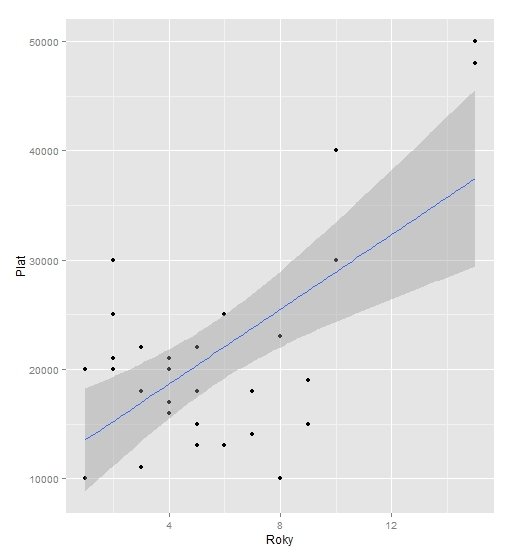
Proměnné
N = 30
Roky:
- M (5.6), SE (3.7),
- Min (1), Max (15)
Plat:
- M (21 400), SE (9 828),
- Min (10 000), Max (50 000)
Průsečík a směrnice
Y' = a + bX
Y' = b0 + b1X1
a, resp. b0 = 11829
b, resp. b1 = 1709
2. Model
sT2 = sM2 + sR2 (neboli ssT = ssres + ssreg)
R2 = ssM2 / ssT2
Přímka (model) je proložena daty tak, aby jim co nejlépe odpovídala.
Metoda odhadu nejmenších čtverců (Least Squares Estimation)
Suma (druhých mocnin) vzdáleností modelu od dat je nejmenší možná
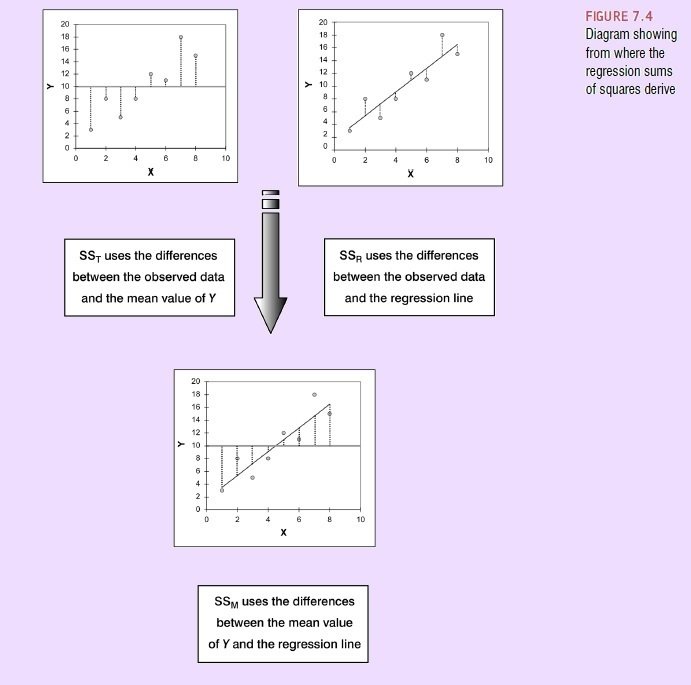
SSM = Rozdíl mezi nulovým modelem (průměr Y) a námi stanoveným modelem (přímkou)
SSR = Rozdíl mezi daty a námi stanoveným modelem (přímkou)
SST = Rozdíl mezi daty a nulovým modelem (průměr Y)
R2 = Podíl rozptylu závislé (outcome) proměnné vysvětlené modelem (= koeficient determinance)
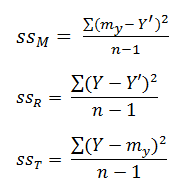
2. Metoda nejmenších čtverců graficky
dle Field, 2009, s. 203
2. Koeficienty
bi
Vyjadřuje nárůst Y’ při nárůstu Xi o jednu jednotku v jednotkách Y, při kontrole všech ostatních prediktorů (tj. semiparciální korelace); jedinečný přínos
- K porovnání síly prediktoru v různých skupinách, modelech, vzorcích
βi ; Beta
Vyjadřuje nárůst Y’ při nárůstu Xi o 1; jsou-li Xi i Y standardizovány, při kontrole všech ostatních prediktorů (tj. semiparciální korelace), jedinečný přínos
- K porovnání prediktorů mezi sebou v rámci jednoho modelu
- K porovnání různě operacionalizovaného prediktoru v různých modelech
- Ukazatel velikosti účinku
b0
Po vycentrování (odečtení průměru od všech hodnot X1) odpovídá průměru Y.
2a. Příklad - Model a koeficienty
Y' = b0 + b1X1
Prediktory
- Y' = 11 828 + 1709*X
- Pracovník, který ve firmě působí 1 rok, by si dle modelu měl vydělat 13537 Kč

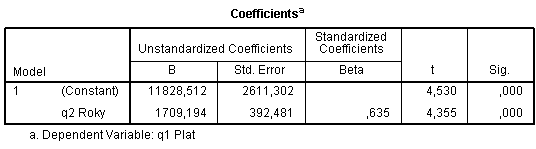
Model
- Zvolený model vysvětluje 40 % rozptylu, tedy
- Délka praxe odpovídá za výši platu ze 40 %
3. Předpoklady použití I.
Proměnné
1. Povaha proměnných - spojité, kvantitativní a kardinální nebo dummy (jen v případě prediktorů).
2. Nenulová variabilita prediktorů (tj. nejde o konstantu).
Prediktory
3. Absence (dokonalé) multikolinearity - prediktory by spolu neměly vysoce korelovat.
4. Prediktory nekorelují s vnějšími proměnnými - absence třetí (intervenující, vnější) proměnné.
"To draw conclusions about a population based on a regression analysis done on a sample, several assumptions must be true." (Field, 2009 , s. 220)
3. Předpoklady použití II.
Rezidua
5. Homoskedascita - rozptyl reziduí by měl být konstantní napříč různými úrovněmi prediktoru
6. Nezávislost reziduí - Reziduální hodnoty kterýchkoliv dvou případů by spolu neměly souviset.
7. Normálně rozložená rezidua - jejich rozložení by mělo být náhodné
Outcome
8. Nezávislost kterýchkoliv dvou hodnot závislé proměnné (každá hodnota v rámci ní pochází z unikátního zdroje)
9. Linearita - přímka jako vhodný model popisu dat.
3a. Příklad
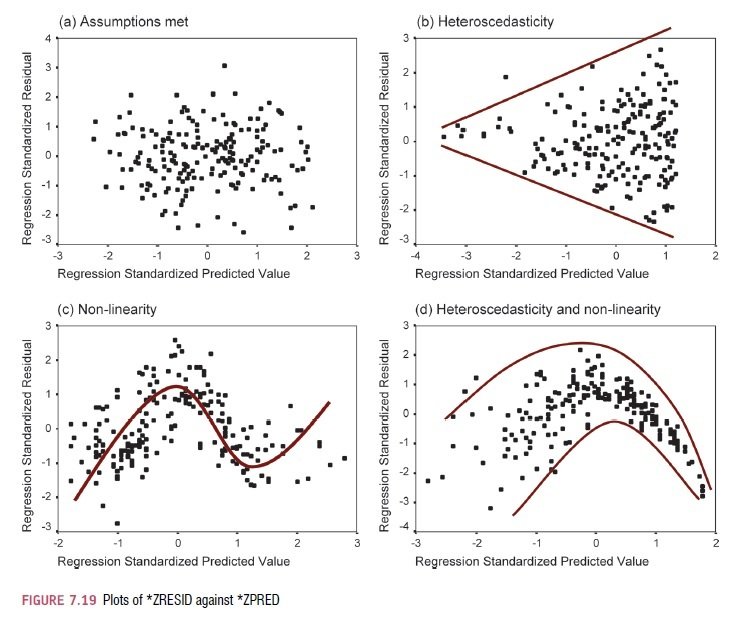
dle Field, 2009, s. 248
4. Diagnostika I. - Outliery a vlivné případy
Nemají některé případy příliš velký vliv na výsledky regrese?
-
Outliery – mohou zvyšovat i snižovat b
- Rezidua – případy s vysokými rezidui regrese predikuje nejhůř, standardizovaná, ± 3
-
Vlivné případy – případy, které nejvíc ovlivňují parametry modelu
- Co se stane s parametry regrese, když případ odstraníme?
- DFBeta – rozdíl mezi parametrem s a bez, standardizované > 1
- DFFit – rozdíl mezi predikovanou hodnotou a predikovanou hodnotou bez případu (adjustovanou)
- Cookova vzdálenost > 1
- Leverage > 2( k+1)/ n , kde k = počet prediktorů, n= velikost vzorku
-
Případy s vysokými rezidui či vlivné případy NEODSTRAŇUJEME
- …leda by šlo o zjevnou chybu v datech či vzorku
- ...leda by nám šlo výhradně o zpřesnění predikce (nikoli o testy hypotéz)
4. Diagnostika II. - Kolinearita
- Když dva prediktory vysvětlují tutéž část variability závislé proměnné, jeden z nich je téměř zbytečný
- Komplikuje porovnávání síly prediktorů
- Snižuje stabilitu odhadu parametrů
- V extrému (když lze jeden prediktor přesně vypočítat z ostatních) regresi úplně znemožňuje
-
"Rules of Thumb"
- Korelace nad 0,9
- Tolerance (= 1/VIF) cca pod 0,1
- VIF (= 1/tolerance) cca nad 10)
5. Dummy coding I. - obecně a postup

Dummy proměnné - kategorické proměnné upravené tak, aby mohly vstoupit do (vícenásobné) lineární regrese
Postup (dle Field, 2009, s. 254)
5. Dummy coding II. - Kódování
Indikátorové kódování (Indicator coding)
- Referenční kategorie = 0
Efektové kódování (Effect coding)
- Referenční kategorie = -1
| Vysokoškolské | Středoškolské | Vysokoškolské | Středoškolské | ||
|---|---|---|---|---|---|
| Vysokoškolské | 1 | 1 | 0 | 1 | 0 |
| Středoškolské | 2 | 0 | 1 | 0 | 1 |
| Základní | 3 | 0 | 0 | -1 | -1 |
| Úroveň vzdělání | Původní hodnota | Indikátorové kódování | Efektové kódování |
|---|
5. Dummy coding III. - Interpretace
Y = b0 +bA1XA1 + bA2XA2 + … + bmXm + e
- Po dosazení do regresní rovnice predikujeme případu průměr jeho skupiny (pokud nejsou žádné další prediktory).
-
Indikátorové kódování
- bAi udává rozdíl průměrných hodnot Y mezi indikovanou skupinou a referenční skupinou; sig b Ai referenční skupinou; sig bAi znamená sig rozdílu
- bAi udává o kolik nám členství ve skupině zvyšuje/snižuje predikovanou hodnotu oproti referenční skupině
- b0 udává (při absenci jiných prediktorů) průměr Y v referenční skupině
-
Efektové kódování
- bAi udává rozdíl průměrných hodnot Y mezi indikovanou skupinou a celkovým průměrem
- b0 udává (při absenci jiných prediktorů) celkový průměr
5a. Příklad

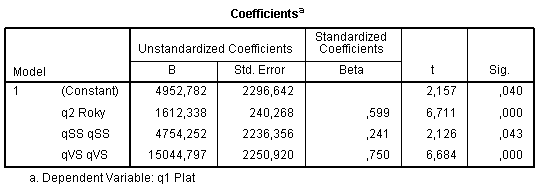
Interpretace - Model:
- Přidání stupně vzdělání zlepšilo predikční vlastnosti modelu na 80 %.
- Výše platu ve firmě BD Technologies se tedy z 80 % odvíjí od let praxe a dosaženého stupně vzdělání.
Interpretace - Prediktory
- Středoškolské vzdělání garantuje ve srovnání s tím základním průměrně o 5 tisíc Kč větší plat.
- Vysokoškolské vzdělání garantuje ve srovnání s tím základním průměrně o 0,75 směrodatnou odchylku větší plat.
Y = b0 +b1Plat + b2SŠ + b3VŠ + e
6. Vkládání prediktorů I.
SPSS nabízí 4 způsoby:
ENTER (Forced entry)
Vloží všechny prediktory najednou
BLOCKWISE
Vkládání sady prediktorů po blocích
STEPWISE
FORWARD
Vybere prediktory, které nejlépe odpovídají datům - až po stanovenou mez
BACKWARD
Vyřadí prediktory nejhůře odpovídající datům - až po stanovenou mez
6. Vkládání prediktorů - dovětek k BLOCKWISE I.
- Prediktory vkládáme po skupinách (popř. jednotlivě) v teoreticky zdůvodněném pořadí
-
Teoreticky zdůvodněné pořadí umožňuje rozdělit rozptyl Y na smysluplné části (variance partitioning)
- Změna pořadí prediktorů změní velikost těch částí
-
Zajímá nás schopnost sady prediktorů vylepšit model
- Srovnání různých oblastí vlivu na zkoumaný jev
- Zkoumání inkrementální validity
Obvyklé řazení bloků
-
Od známých k neznámým vlivům
- kontrola intervenujících proměnných
- Minimalizace chyby 1. typu
-
Podle výzkumné relevance
- Od ústředních po „co kdyby“; maximalizace statistické síly
6. Vkládání prediktorů - dovětek k BLOCKWISE II.
Obvyklý postup
- Na základě teoretických rozvah stanovíme různé modely, jejichž srovnání je potenciálně zajímavé
- Možnost testovat nárůst (inkrement) R2
- Až v druhé řadě se zabýváme jednotlivými regresními koeficienty v modelu, který je nejúplnější/nejlepší
7. Reportování (více např. dle APA, 2001)
1. Popisné statistiky
- Y, X
- Spojité - N, Min, Max, M, SD, Me
- Kategorické - N, %, dummy coding
- Korelační matice
2. Předpoklady použití
- Konstatování (např. o povaze proměnných
- Výpočet (např. outliery a vlivné příklady)
3. Model
- F-test
- Koeficient determinance (R2)
- p
4. Prediktory
- B
- SE či intervaly spolehlivosti
- Beta
- p
Děkuji za pozornost!
Zdroje
American Psychological Association. (2001). Publication manual of the American Psychological Association (6th ed.). Washington, DC: APA.
Field, A. (2009). Discovering statistics using SPSS, 3th Ed. Los Angeles: Sage.
Fox, J. (2016). Applied Regression Analysis and Generalized Linear Models, 3th Ed. Los Angeles: Sage.
Galton, F. (1886). Regression towards mediocrity in hereditary stature. Journal of the Anthropological Institute, 15, pp. 246-63. Dostupné online z "http://galton.org/essays/1880-1889/galton-1886-jaigi-regression-stature.pdf"
Robotková, A., & Ježek, S. (2012). Vícenásobná lineární regrese. Prezentace ke kurzu PSY252.
Úkol
Na zvolených datech proveďte vícenásobnou lineární regresi.
Požadavky:
- Minimálně jeden prediktor spojité (kardinální etc.) povahy a minimálně jeden prediktor kategorické (dummy) povahy
- Celý proces - od popisu proměnných přes předpoklady a interpretaci výsledků po diagnostiku modelu
Bonus:
-
1 bod obdrží ten, kdo
- Představí dataset a proměnné na úrovni konceptů (např. z jakých položek se skládá škála well-beingu) a zároveň
- Volbu proměnných (a hypotéz) a interpretaci výsledků podloží odbornými zdroji
Vícenásobná lineární regrese
By Vít Gabrhel
Vícenásobná lineární regrese
- 1,306



