(Vícenásobná) lineární regrese
(Multiple) Linear Regression
Vít Gabrhel
vit.gabrhel@mail.muni.cz
FSS MU,
23. 10. 2017

Harmonogram
Historie
Teorie
Model
Předpoklady použití
Diagnostika
Dummy coding
Vkládání prediktorů
Mediace
Mediace
Reportování výsledků
O původu lineární regrese I.


O původu lineární regrese II.
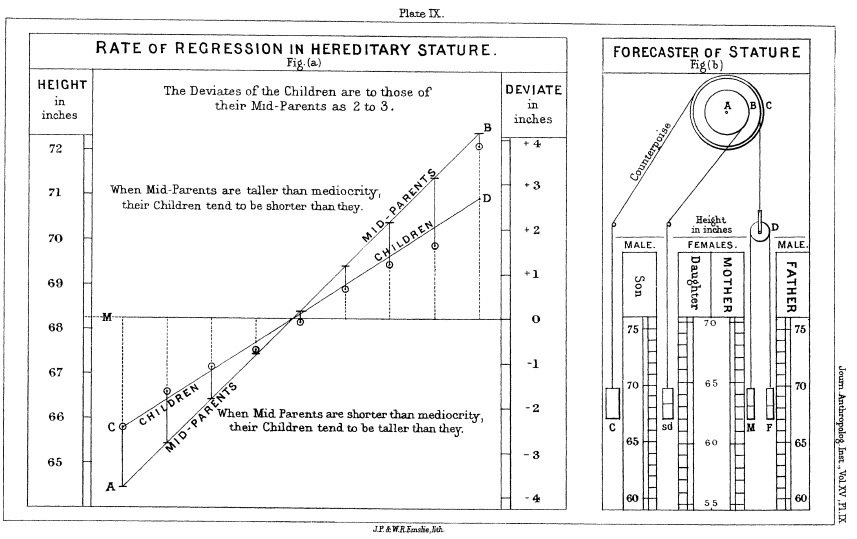
O původu lineární regrese III.
Jak to, že děti vysokých rodičů samy bývají vysoké, ale ne tak jako jejich rodiče?
Jak to, že děti útlých rodičů samy bývají útlé, ale ne tak útlé jako jejich rodiče?
Jak to, že nejlepší atlet minulé sezóny letos podává o něco horší výkon než loni?
Regrese k průměru (Regression towards mediocrity)
"It appeared from these experiments that the offspring did not tend to resemble their parent seeds in size, but to be always more mediocre than they-to be smaller than the parents, if the parents were large; to be larger than the parents, if the parents were very small."
"The point of convergence was considerably below the average size of the seeds contained in the large bagful I bought at a nursery garden, out of which I selected those that were sown, and I had some reason to believe that the size of the seed towards which the produce converged was similar to that of an average seed taken out of beds of self-planted specimens."
Galton, 1886, s. 246
1. O původu lineární regrese IV.

K čemu slouží lineární regrese?
Lineární regrese
-
Nakolik lze z IQ skóru usuzovat o výkonu v matematice?
- Predikce
Vícenásobná lineární regrese
-
Přispívá k výši platu kromě úrovně vzdělání také pohlaví?
-
Predikce
-
Inkrementální validita
-
Statistická kontrola
-
Notace
Y = Y' + e
Lineární regrese
Y' = a + bX
Y' = b0 + b1X1
Vícenásobná lineární regrese
Y' = a + bnXn
Y' = b0 + b1X1 + b2X2 + ... + bnXn + e
Y = Predikovaná (= závislá; outcome) proměnná
Y' = Náš model
e = Chyba měření
a nebo b0 = průsečík (= intercept)
b nebo b1...n = směrnice (= slope)
X1...n = Prediktor (= nezávislá proměnná; predictor)
Grafické znázornění
Y = Y' + e
Y' = a + bX
Y' = b0 + b1X1
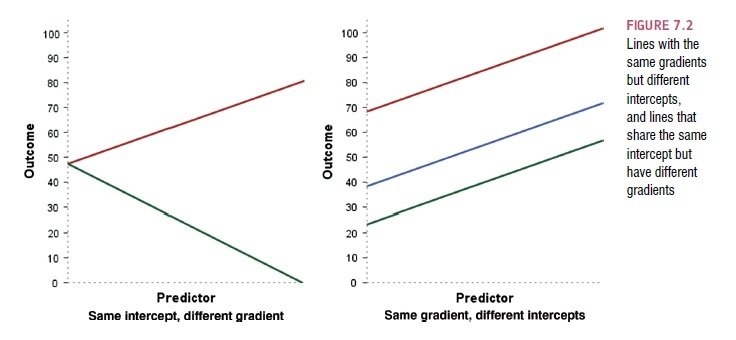
dle Field, 2009, s. 199

# Nahrání dat
Humor = read.csv2("data.csv", header = TRUE)
HumorClean = na.omit(Humor)
View(HumorClean)
# Nastavení dat
levels(HumorClean$gender) = c("Muž", "Žena")
lapply(HumorClean, class)
Model
sT2 = sM2 + sR2 (neboli ssT = ssres + ssreg)
R2 = ssM2 / ssT2
Přímka (model) je proložena daty tak, aby jim co nejlépe odpovídala.
Metoda odhadu nejmenších čtverců (Least Squares Estimation)
Suma (druhých mocnin) vzdáleností modelu od dat je nejmenší možná
SSM = Rozdíl mezi nulovým modelem (průměr Y) a námi stanoveným modelem (přímkou)
SSR = Rozdíl mezi daty a námi stanoveným modelem (přímkou)
SST = Rozdíl mezi daty a nulovým modelem (průměr Y)
R2 = Podíl rozptylu závislé (outcome) proměnné vysvětlené modelem (= koeficient determinance)
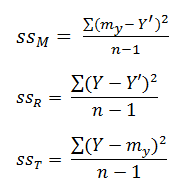
2. Metoda nejmenších čtverců graficky
dle Field, 2009, s. 203
Model
Příklad
ModelHumoru <- lm(formula = agressive ~ age + gender, data = HumorClean)
# Compute the summary statistics for model
# Generic functions (summary) change their behaviour based on an object's class.
summary(ModelHumoru)
# Perform an analysis of variance on model
anova(ModelHumoru)
# Produce diagnostic plots for model
plot(ModelHumoru)
# Prediction based on the fitted function model_erc
predict(ModelHumoru)
Koeficienty
bi
Vyjadřuje nárůst Y’ při nárůstu Xi o jednu jednotku v jednotkách Y, při kontrole všech ostatních prediktorů (tj. semiparciální korelace); jedinečný přínos
- K porovnání síly prediktoru v různých skupinách, modelech, vzorcích
βi ; Beta
Vyjadřuje nárůst Y’ při nárůstu Xi o 1; jsou-li Xi i Y standardizovány, při kontrole všech ostatních prediktorů (tj. semiparciální korelace), jedinečný přínos
- K porovnání prediktorů mezi sebou v rámci jednoho modelu
- K porovnání různě operacionalizovaného prediktoru v různých modelech
- Ukazatel velikosti účinku
b0
Po vycentrování (odečtení průměru od všech hodnot X1) odpovídá průměru Y.
Koeficienty
Příklad
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 2.9329217 0.0347063 84.507 <2e-16 ***
age 0.0006529 0.0011434 0.571 0.568
gender 0.0407037 0.0249082 1.634 0.103
Bety:
install.packages("QuantPsyc")
library(QuantPsyc)
lm.beta(ModelHumoru)

Předpoklady použití I.
Proměnné
1. Povaha proměnných - spojité, kvantitativní a kardinální nebo dummy (jen v případě prediktorů).
2. Nenulová variabilita prediktorů (tj. nejde o konstantu).
Prediktory
3. Absence (dokonalé) multikolinearity - prediktory by spolu neměly vysoce korelovat.
4. Prediktory nekorelují s vnějšími proměnnými - absence třetí (intervenující, vnější) proměnné.
"To draw conclusions about a population based on a regression analysis done on a sample, several assumptions must be true." (Field, 2009 , s. 220)
Předpoklady použití I.
Příklad
Povaha proměnných a nenulová variabilita
# Ověření skrze funkce (např.):
- lapply(HumorClean[, 33:39], class),
- summary(HumorClean),
- describe(HumorClean) # library("psych")
Multikolinearita
# Ověření skrze funkce (např.):
- library("car")
- vif(ModelHumoru) # variance inflation factors
- sqrt(vif(ModelHumoru)) > 2 # problem?
- Humor_Selected = subset(HumorClean, select = c(agressive, gender, age))
- library(Rcmdr)
- rcorr.adjust(Humor_Selected)
Předpoklady použití II.
Rezidua
5. Homoskedascita - rozptyl reziduí by měl být konstantní napříč různými úrovněmi prediktoru
6. Nezávislost reziduí - Reziduální hodnoty kterýchkoliv dvou případů by spolu neměly souviset.
7. Normálně rozložená rezidua - jejich rozložení by mělo být náhodné
Outcome
8. Nezávislost kterýchkoliv dvou hodnot závislé proměnné (každá hodnota v rámci ní pochází z unikátního zdroje)
9. Linearita - přímka jako vhodný model popisu dat.
Homoskedascita a linearita
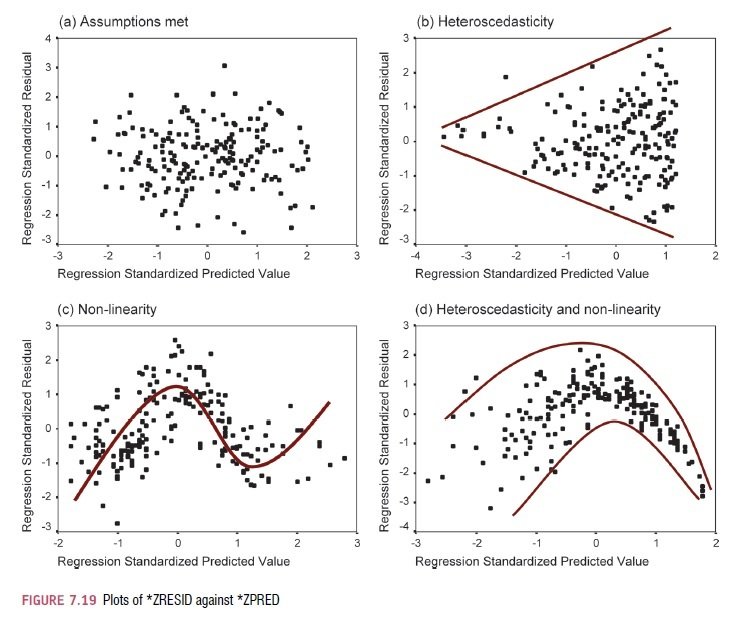
dle Field, 2009, s. 248
Předpoklady použití II.
Příklad
Homoskedascita
# Evaluate homoscedasticity
# non-constant error variance test
ncvTest(ModelHumoru)
# plot studentized residuals vs.
# fitted values
spreadLevelPlot(ModelHumoru)
Nezávislost reziduí
# Test for Autocorrelated Errors
durbinWatsonTest(ModelHumoru)
Normálně rozložená rezidua
# distribution of studentized residuals
library(MASS)
sresid <- studres(ModelHumoru)
hist(sresid, freq=FALSE,
main="Distribution of Studentized Residuals")
Rezidua
Předpoklady použití II.
Příklad
Outcome
Linearita
# component + residual plot
crPlots(ModelHumoru)
Diagnostika I. - Outliers a Influentials
Nemají některé případy příliš velký vliv na výsledky regrese?
-
Outliery – mohou zvyšovat i snižovat b
- Rezidua – případy s vysokými rezidui regrese predikuje nejhůř, standardizovaná, ± 3
-
Vlivné případy – případy, které nejvíc ovlivňují parametry modelu
- Co se stane s parametry regrese, když případ odstraníme?
- DFBeta – rozdíl mezi parametrem s a bez, standardizované > 1
- DFFit – rozdíl mezi predikovanou hodnotou a predikovanou hodnotou bez případu (adjustovanou)
- Cookova vzdálenost > 1
- Leverage > 2( k+1)/ n , kde k = počet prediktorů, n= velikost vzorku
-
Případy s vysokými rezidui či vlivné případy NEODSTRAŇUJEME
- …leda by šlo o zjevnou chybu v datech či vzorku
- ...leda by nám šlo výhradně o zpřesnění predikce (nikoli o testy hypotéz)

Diagnostika II. - Kolinearita
- Když dva prediktory vysvětlují tutéž část variability závislé proměnné, jeden z nich je téměř zbytečný
- Komplikuje porovnávání síly prediktorů
- Snižuje stabilitu odhadu parametrů
- V extrému (když lze jeden prediktor přesně vypočítat z ostatních) regresi úplně znemožňuje
-
"Rules of Thumb"
- Korelace nad 0,9
- Tolerance (= 1/VIF) cca pod 0,1
- VIF (= 1/tolerance) cca nad 10)
Diagnostika I. - Outliers a Influentials
Příklad
Outliers
# Bonferonni p-value for most extreme observations
outlierTest(ModelHumoru)
#qq plot for studentized resid
qqPlot(ModelHumoru, main="QQ Plot")
# leverage plots
leveragePlots(ModelHumoru)
Influentials
# Cook's D plot
# identify D values > 4/(n-k-1)
cutoff <- 4/((nrow(HumorClean)-length(ModelHumoru$coefficients)-2))
plot(ModelHumoru, which=4, cook.levels=cutoff)
# Influence Plot
influencePlot(ModelHumoru, id.method="identify", main="Influence Plot", sub="Circle size is proportial to Cook's Distance" )
Dummy coding I. - obecně a postup

Dummy proměnné - kategorické proměnné upravené tak, aby mohly vstoupit do (vícenásobné) lineární regrese
Postup (dle Field, 2009, s. 254)
Dummy coding II. - Kódování
Indikátorové kódování (Indicator coding)
- Referenční kategorie = 0
Efektové kódování (Effect coding)
- Referenční kategorie = -1
| Vysokoškolské | Středoškolské | Vysokoškolské | Středoškolské | ||
|---|---|---|---|---|---|
| Vysokoškolské | 1 | 1 | 0 | 1 | 0 |
| Středoškolské | 2 | 0 | 1 | 0 | 1 |
| Základní | 3 | 0 | 0 | -1 | -1 |
| Úroveň vzdělání | Původní hodnota | Indikátorové kódování | Efektové kódování |
|---|
Dummy coding III. - Interpretace
Y = b0 +bA1XA1 + bA2XA2 + … + bmXm + e
- Po dosazení do regresní rovnice predikujeme případu průměr jeho skupiny (pokud nejsou žádné další prediktory).
-
Indikátorové kódování
- bAi udává rozdíl průměrných hodnot Y mezi indikovanou skupinou a referenční skupinou; sig b Ai referenční skupinou; sig bAi znamená sig rozdílu
- bAi udává o kolik nám členství ve skupině zvyšuje/snižuje predikovanou hodnotu oproti referenční skupině
- b0 udává (při absenci jiných prediktorů) průměr Y v referenční skupině
-
Efektové kódování
- bAi udává rozdíl průměrných hodnot Y mezi indikovanou skupinou a celkovým průměrem
- b0 udává (při absenci jiných prediktorů) celkový průměr
Dummy coding
hsb2 <- read.csv("hsb2.csv")
1. The factor function
# creating the factor variable
hsb2$race.f <- factor(hsb2$race)
is.factor(hsb2$race.f)
summary(lm(write ~ race.f, data = hsb2))
Vkládání prediktorů I.
4 způsoby:
ENTER (Forced entry)
Vloží všechny prediktory najednou
BLOCKWISE
Vkládání sady prediktorů po blocích
STEPWISE
FORWARD
Vybere prediktory, které nejlépe odpovídají datům - až po stanovenou mez
BACKWARD
Vyřadí prediktory nejhůře odpovídající datům - až po stanovenou mez
6. Vkládání prediktorů - dovětek k BLOCKWISE I.
- Prediktory vkládáme po skupinách (popř. jednotlivě) v teoreticky zdůvodněném pořadí
-
Teoreticky zdůvodněné pořadí umožňuje rozdělit rozptyl Y na smysluplné části (variance partitioning)
- Změna pořadí prediktorů změní velikost těch částí
-
Zajímá nás schopnost sady prediktorů vylepšit model
- Srovnání různých oblastí vlivu na zkoumaný jev
- Zkoumání inkrementální validity
Obvyklé řazení bloků
-
Od známých k neznámým vlivům
- kontrola intervenujících proměnných
- Minimalizace chyby 1. typu
-
Podle výzkumné relevance
- Od ústředních po „co kdyby“; maximalizace statistické síly
6. Vkládání prediktorů - dovětek k BLOCKWISE II.
Obvyklý postup
- Na základě teoretických rozvah stanovíme různé modely, jejichž srovnání je potenciálně zajímavé
- Možnost testovat nárůst (inkrement) R2
- Až v druhé řadě se zabýváme jednotlivými regresními koeficienty v modelu, který je nejúplnější/nejlepší
Mediace
A mediation analysis is typically conducted to better understand an observed effect of an IV on a DV or a correlation between X and Y
- Why, and how, does X influence/correlates with Y?
If X and Y are correlated BECAUSE of the mediator M, then
(X -> M -> Y)
- Y = B0 + B1M + e
&
- M = B0 + B1X + e
&
- Y = B0 + B1M + B2X + e
What will happen to the predictive value of X?
In other words, will B2 be significant?
Mediace
A mediator variable (M) accounts for some or all of the relationship between X and Y
- Some: Partial mediation
- All: Full mediation
Mediace
Příklad
# Summary statistics
describeBy(med, med$cond)
# Create a boxplot of the data
boxplot(formula = med$iq ~ med$cond, main = "Boxplot", xlab = "Group condition", ylab = "IQ")
med <- read.csv2("med.csv", header = TRUE)
library("psych")
Mediace
Příklad
# Run the three regression models
model_yx <- lm(med$iq ~ med$cond)
model_mx <- lm(med$wm ~ med$cond)
model_yxm <- lm(med$iq ~ med$cond + med$wm)
# Make a summary of the three models
summary(model_yx)
summary(model_mx)
summary(model_yxm)
Mediace
Příklad - Sobelův test
library("multilevel")
# Compare the previous results to the output of the sobel function
model_all <- sobel(med$cond, med$wm, med$iq)
# Print out model_all
model_all

Moderace
Představení
- Korelační design
- Předpokládáme souvislost mezi proměnnými X a Y
- Moderátor (Z) zavádíme kvůli předpokladu, že korelace mezi X a Y NENÍ konzistentní napříč rozložením (různými úrovněmi) Z.
- Experimentální design
- Manipulace s nezávislou proměnnou (X) vede ke změně v závislé proměnné (Y)
- Moderátor (Z) zavádíme z toho kvůli předpokladu, že vliv (účinek) X na Y NENÍ konzistentní napříč rozložením (různými úrovněmi) Z.
Moderace
Model
- Pokud jsou oboje X a Z spojité (resp. intervalové úrovně měření)
- Y = B0 + B1X + B2Z + B3(X*Z) + e
- Pokud je X kategorická a Z spojitá (3 úrovně X)
- Y = B0 + B1(D1) + B2(D2) + B3Z + B4(D1*Z) + B5(D2*Z) + e
- 1. řádek = hlavní efekt
- 2. řádek = moderace
Moderace
Příklad
mod = read.csv2("mod.csv", header = TRUE)
# Summary statistics
describeBy(mod, mod$condition)
# Create a boxplot of the data
boxplot(formula = mod$iq ~ mod$condition, main = "Boxplot", xlab = "Group condition", ylab = "IQ")
# Create subsets of the three groups
# Make the subset for the group condition = "control"
mod_control <- subset(mod, mod$condition == "control")
# Make the subset for the group condition = "threat1"
mod_threat1 <- subset(mod, mod$condition == "threat1")
# Make the subset for the group condition = "threat2"
mod_threat2 <- subset(mod, mod$condition == "threat2")
# Calculate the correlations
cor(mod_control$iq, mod_control$wm)
cor(mod_threat1$iq, mod_threat1$wm)
cor(mod_threat2$iq,mod_threat2$wm)
Moderace
Příklad
# Model without moderation (tests for "first-order effects")
model_1 <- lm(mod$iq ~ mod$wm + mod$d1 + mod$d2)
# Make a summary of model_1
summary(model_1)
# Create new predictor variables
wm_d1 <- mod$wm * mod$d1
wm_d2 <- mod$wm * mod$d2
# Model with moderation
model_2 <- lm(mod$iq ~ mod$wm + mod$d1 + mod$d2 + wm_d1 + wm_d2)
# Make a summary of model_2
summary(model_2)
# Compare model_1 and model_2
anova(model_1, model_2)
# Choose colors to represent the points by group
color <- c("red","green","blue")
# Illustration of the first-order effects of working memory on IQ
ggplot(mod, aes(x = wm, y = iq)) + geom_smooth(method = "lm", color = "black") +
geom_point(aes(color = condition))
# Illustration of the moderation effect of working memory on IQ
ggplot(mod, aes(x = wm, y = iq)) +
geom_smooth(aes(group = condition), method = "lm", se = T, color = "black", fullrange = T) +
geom_point(aes(color = condition))
library("ggplot2")
Mediace a moderace
A moderator has influence over
other effects or relationships, whereas
the mediator explains a relationship.
Reportování (více např. dle APA, 2001)
1. Popisné statistiky
- Y, X
- Spojité - N, Min, Max, M, SD, Me
- Kategorické - N, %, dummy coding
- Korelační matice
2. Předpoklady použití
- Konstatování (např. o povaze proměnných
- Výpočet (např. outliery a vlivné příklady)
3. Model
- F-test
- Koeficient determinance (R2)
- p
4. Prediktory
- B
- SE či intervaly spolehlivosti
- Beta
- p
Děkuji za pozornost!
Zdroje
American Psychological Association. (2001). Publication manual of the American Psychological Association (6th ed.). Washington, DC: APA.
Field, A. (2009). Discovering statistics using SPSS, 3th Ed. Los Angeles: Sage.
Fox, J. (2016). Applied Regression Analysis and Generalized Linear Models, 3th Ed. Los Angeles: Sage.
Galton, F. (1886). Regression towards mediocrity in hereditary stature. Journal of the Anthropological Institute, 15, pp. 246-63. Dostupné online z "http://galton.org/essays/1880-1889/galton-1886-jaigi-regression-stature.pdf"
Robotková, A., & Ježek, S. (2012). Vícenásobná lineární regrese. Prezentace ke kurzu PSY252.
PSY532, PSY232 - 5. Vícenásobná lineární regrese
By Vít Gabrhel
PSY532, PSY232 - 5. Vícenásobná lineární regrese
- 1,375



