ANOVA

Vít Gabrhel

vit.gabrhel@mail.muni.cz

FSS MU,

6. 11. 2017

Harmonogram

1. ANOVA

 

2. Faktoriální ANOVA

 

ANOVA

Úvod

ANOVA = ANalysis Of VAriance

 

• Slouží pro srovnání skupinových průměrů napříč 3 a více skupinami/podmínkami 
• Dvě výchozí varianty:
  • Between design: oddělené, na sobě nezávislé skupiny (ANOVA, ANCOVA, faktoriální ANOVA atd.)
    • Liší se jednotlivé kraje v ČR z hlediska průměrné mzdy?
  • Within design: srovnání skupinového průměru napříč různými podmínkami (Repeated Measures ANOVA)
    • Lišily se průměrné výdaje domácností na pohonné hmoty během posledních 5 let?

One-Way ANOVA

Data: Cognitive training

• Four independent groups (8, 12, 17, 19 sessions)
• Measured IQ before and after training
• Dependent variable is IQ gain
• Null hypothesis: All groups are equal (i.e. all groups have equal IQ gain)
• Alternative hypothesis: More training leads to larger IQ gain

One-Way ANOVA

Data: Cognitive training

setwd()
dir()

 

install.packages("readxl")
library("readxl")

 

excel_sheets("ANOVA.xlsx")

ANOVA = read_excel("ANOVA.xlsx", sheet = 1)
View(ANOVA)

 

ANOVA$condition2 = factor(ANOVA$condition, order = TRUE, levels = c("8 days", "12 days", "17 days", "19 days"))

One-Way ANOVA

F-test a F-Ratio

• Null hypothesis: all groups are equal
• ANOVA provides a significance test
  • Můžeme určit kritickou hodnotu (na určité hladině významnosti) a testovat, zda ji hodnota F v našem výzkumu překračuje, tj. testovat statistickou významnost nalezených rozdílů mezi skupinami
• Test statistic is the F-test (or F-ratio)

Variance between groups

Variance within groups

F =

• Poměr toho, co model vysvětlit dokáže, ku tomu, co vysvětlit nedokáže
• Large F-ratio indicates significant effect
  • Čím vyšší F, tím více záleží na rozdělení lidí do jednotlivých skupin, tj. tím více se skupiny od sebe liší v závislé proměnné 

One-Way ANOVA

F-test a F-Ratio

Jak získáme příslušnou p-hodnotu?

• Obdoba t-testu a "rodině" t-rozložení
• "Rodina" F-rozložení se odvíjí od:
  • Počtu pozorování (případů) ve vzorku
  • Počtu srovnávaných skupin

One-Way ANOVA

F-test a F-Ratio

# Create the vector x
x <- seq(from = 0, to = 10, length = 2000)

 

# Evaluate the densities

y_1 <- df(x, 3, 100)
y_2 <- df(x, 1, 1)
y_3 <- df(x, 2, 100)
y_4 <- df(x, 3, 30)
y_5 <- df(x, 3, 500)
y_6 <- df(x, 3, 50)
y_7 <- df(x, 6, 1000)

 

# Plot the densities
plot(x, y_1, col = 1, type = "l")
lines(x, y_2, col = 2)
lines(x, y_3, col = 3)
lines(x, y_4, col = 4)
lines(x, y_5, col = 5)
lines(x, y_6, col = 6)
lines(x, y_7, col = 7)

# Add the legend

legend("topright", title = "F distributions",
       c("df = (3, 100)", "df = (1, 1)", "df = (2, 100)", "df = (3, 30)",
         "df = (3, 500)", "df = (3, 50)", "df = (6, 1000)"),
       col = c(1, 2, 3, 4, 5, 6, 7), lty = 1)

One-Way ANOVA

Summary Table

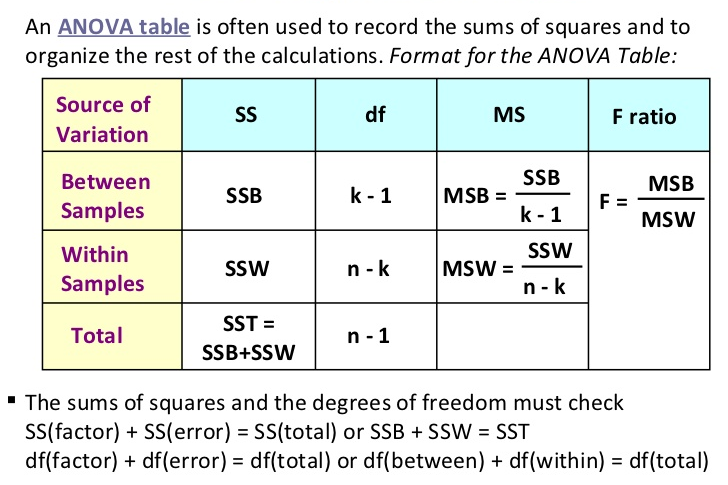
One-Way ANOVA

F-test a F-Ratio

Prozkoumání dat

 # Summary statistics by group

 library(psych)
 describeBy(ANOVA, group = ANOVA$condition2)

 

# Boxplot

 library(ggplot2)
 bp1 = ggplot(ANOVA, aes(condition2, iq))

 bp1 + geom_boxplot(aes(fill=condition2), alpha=I(0.5)) +
  geom_point(position="jitter", alpha=0.5) +
  geom_boxplot(outlier.size=0, alpha=0.5) +
  theme(
    axis.title.x = element_text(face="bold", color="black", size=12),
    axis.title.y = element_text(face="bold", color="black", size=12),
    plot.title = element_text(face="bold", color = "black", size=12)) +
  labs(x="Condition",
       y = "IQ gain",
       title= "IQ gain by the days of training") + theme(legend.position='none')

One-Way ANOVA

F-test a F-Ratio

Funkce aov

 aov(dependent_var ~ independent_var)

 summary()

 

 # Apply the aov function
 anova_wm <- aov(iq ~ condition2, data = ANOVA)

 

 # Look at the summary table of the result
 summary(anova_wm)

One-Way ANOVA

Velikost účinku

library(lsr)

etaSquared(anova_wm, type = 2, anova = FALSE)

library(sjstats)

anova_wm2 <- lm(iq ~ condition2, data = ANOVA)

r2(anova_wm2, n = NULL)

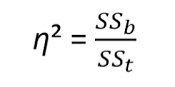
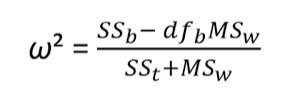
One-Way ANOVA

Předpoklady použití

Povaha proměnných

• "Závislá" proměnná kardinální úrovně měření

 

Normalita rozložení závislé proměnné

• V rámci každé sledované skupiny
• Narušení nepředstavuje závažný problém, pokud jsou skupiny stejně velké + mají velikost alespoň okolo 30
• Neparametrická alternativa – Kruskal-Wallisův test

 

Homogenita rozptylu

• Sledujeme Levenův F-test, nulová hypotéza hovoří o homogenitě napříč skupinami
  • Pokud Levenův F-test vychází statisticky signifikantní:
• Sledujeme poměr rozptylu u skupin s největším a nejmenším rozptylem, přičemž chceme, aby byl tento poměr menší než 3
• Narušení by nemělo vadit, pokud jsou skupiny stejně velké
• Při narušení lze použít Welchovo F

​

Nezávislost pozorování

One-Way ANOVA

Předpoklady použití

install.packages("car")

library("car")

If you don't specify additional arguments, the deviation scores are calculated by comparing each score to its group median.

• This is the default behaviour, even though they are typically calculated
  by comparing each score to its group mean.
• If you want to use means and not medians, add an argument center
  = mean. Do this now and compare the results to the first test.

 

# Levene's test
leveneTest(iq ~ as.factor(condition2), data = ANOVA)
# Levene's test with center = mean
leveneTest(iq ~ as.factor(condition2), data = ANOVA, center = mean)

One-Way ANOVA

Předpoklady použití

# Normalita rozložení

ggplot(data=ANOVA, aes(ANOVA$iq)) +
  geom_histogram(breaks=seq(0, 20, by = 2),
                 col="red",
                 aes(fill=..count..)) +
  scale_fill_gradient("Count", low = "green", high = "red")+
  labs(title="Histogram for IQ Gain") +
  labs(x="IQ Gain", y="Count") + theme(legend.position='none')

One-Way ANOVA

Welchův F-test

anova_wm_VNE = oneway.test(iq ~ condition2, data=ANOVA, var.equal=FALSE)

anova_wm_VNE
​
anova_wm_VE = oneway.test(iq ~ condition2, data=ANOVA, var.equal=TRUE)

anova_wm_VE

Post-Hoc testy

Úvod

Allow for multiple pairwise comparisons without an increase in the probability of a Type I error

 

Používáme, pokud nemáme dopředu jasné hypotézy

• Srovnávají vše se vším – každou skupinu s každou (ale neumí slučovat skupiny jako kontrasty)

Z principu jsou oboustranné

Je jich mnoho – liší se v několika parametrech:

• Konzervativní (Ch. II. typu) versus Liberální (Ch. I. typu)
  • Most liberal = no adjustment
  • Most conservative = adjust for every possible comparison that could be made
• Ne/vhodné pro rozdílně velké skupiny
• Ne/vhodné pro rozdílné skupinové rozptyly

Post-Hoc testy

Doporučení podle Fielda

Stejně velké skupiny a skupinové rozptyly (ideální situace):

• REGWQ
• Tukey

 

Pokud si chceme být jistí, že P chyby I. typu nepřekročí zvolenou hladinu:

• Bonferroni

 

Pokud jsou velikosti skupin trochu/hodně rozdílné:

• Gabriel
• Hochberg GT2

 

Pokud pochybujeme o shodnosti skupinových rozptylů:

• Games-Howell

Post-Hoc testy

Tukey

# Conduct ANOVA

anova_wm = aov(iq ~ condition2, data = ANOVA)

 

# View summary
summary(anova_wm)

 

# Conduct Tukey procedure
tukey <- TukeyHSD(anova_wm)

 

# Plot confidence intervals
plot(tukey)

Post-Hoc testy

Bonferroni

The Bonferroni correction compensates for that increase by testing each individual hypothesis at a significance level of α/m, where α is the desired overall alpha level and m is the number of hypotheses.

• For example, if a trial is testing m = 20 hypotheses with a desired α = 0.05, then the Bonferroni correction would test each individual hypothesis at α = 0.05/20 =0.0025.

 

# Pairwise t-test

 pairwise.t.test(ANOVA$iq, ANOVA$condition2, p.adjust = "bonferroni")

Kontrasty

Úvod

Umožňují porovnat jednotlivé skupiny v jednom kroku bez nutnosti korigovat hladinu významnosti (bez snížení síly testu)

• Jen když máme dopředu hypotézy
• Kontrastů lze provést tolik, kolik je počet skupin – 1

 

Každý kontrast srovnává 2 průměry

• Průměr skupiny nebo průměr více skupin dohromady
• Např. "19 dnů" vs. "8 dnů" nebo "17 dnů" vs. "12 dnů"

 

Ortogonální (nezávislé) kontrasty

• Skupina použitá v jednom srovnání není použitá v dalším

Neortogonální kontrasty

Kontrasty

Příklad

c1 = c(-1, 0, 0, 1)
c2 = c(0,-1,1,0)
mat <- cbind(c1,c2)
contrasts(ANOVA$condition2) <- mat
model1 <- lm(iq ~ condition2, data = ANOVA)
summary(model1)

 

options(contrasts = c("contr.helmert", "contr.poly"))

contrasts(ANOVA$condition2) <- "contr.helmert"
model1 <- lm(iq ~ condition2, data = ANOVA)
summary(model1)

Faktoriální ANOVA

Úvod

 

 ANOVA s více kategorickými nezávislými proměnnými (faktory) nachází  uplatnění  v experimentálních designech,

• kde pracujeme s několika druhy experimentální manipulace nebo kde chceme zohlednit kromě experimentální manipulace i další proměnné (např. pohlaví)

 

 Uplatnění v neexperimentálních designech, kde chceme posoudit  vliv více kategorických prediktorů najednou

Faktoriální ANOVA

Úvod

Dependent variable

Assess impact on driving error

 

Independent variable

Randomly assign people to different (simulated) driving conditions

• Driving difficulty
• Conversation demand

 

Two independent variables

One continuous dependent variable

Faktoriální ANOVA

Data

library("readxl")

excel_sheets("FANOVA.xlsx")

FANOVA = read_excel("FANOVA.xlsx", sheet = 1)
View(FANOVA)

 

FANOVA$conversation2 = factor(FANOVA$conversation, order = TRUE, levels = c("None demand", "Low demand", "High demand"))

 

FANOVA$driving2 = factor(FANOVA$driving, order = TRUE, levels = c("Easy", "Difficult"))

 

library(psych)

describeBy(FANOVA, group = FANOVA$conversation2)

describeBy(FANOVA, group = FANOVA$driving2)

Faktoriální ANOVA

Úvod

We can test 3 hypotheses:  

• More errors in the difficult simulator?  
• More errors with more demanding conversation?
• More errors due to the interaction of driving difficulty and conversation demand?

Faktoriální ANOVA

Úvod

Three F-ratios

FA = 1st Independent variable, i.e. driving difficulty

FB = 2nd Independent variable, i.e. conversation demand

FAxB  = Interaction between FA and FB

 

Main effect

• Effect of one independent variable ignoring the other one

Interaction effect

• Effect of one independent variable depends on the other

Simple effect

• Effect of one independent variable at a particular level of the other

Faktoriální ANOVA

Interakce

 V různých úrovních jednoho faktoru se rozdíly mezi úrovněmi druhého  faktoru liší (rozdíl rozdílů).

 

 S měnící se úrovní jedné nezávislé proměnné se mění vliv druhé  nezávislé proměnné na závislou proměnnou

 

 Nezávislá proměnná nemusí mít žádný hlavní efekt (main effect)  na závislou proměnnou, ale může ji ovlivňovat tím, že ovlivňuje vliv  druhé nezávislé

 

 Při interpretaci interakcí je obvykle velmi užitečné znázornění formou  grafu.

Faktoriální ANOVA

F-ratio's a Interakce

ggplot(FANOVA,aes(x=factor(conversation2),y=errors,fill=factor(driving2)), color=factor(vs)) +
  stat_summary(fun.y=mean,position=position_dodge(),geom="bar") +
  scale_y_continuous("Errors done while driving") +
  scale_x_discrete("Conversation difficulty") +
  scale_fill_discrete(name ="Driving difficulty", labels=c("Easy", "Difficult"))

 

Factorial_ANOVA = aov(errors ~ conversation2 * driving2, data = FANOVA)
summary(Factorial_ANOVA)

Faktoriální ANOVA

F-ratio's a Interakce

# Interaction plot
interaction.plot(x.factor = FANOVA$conversation2, trace.factor = FANOVA$driving2,
                 response = FANOVA$errors)

 

summary.lm(Factorial_ANOVA)

Faktoriální ANOVA

Velikost účinku

"Eta-squared (η²) and partial eta-squared (ηp²) are biased effect size estimators. I knew this, but I never understood how bad it was. Here’s how bad it is: If η² was a flight from New York to Amsterdam, you would end up in Berlin."

 

"When there is no true effect, η² from small studies can easily give the wrong impression that there is a real small to medium effect, just due to the bias. Your p-value would not be statistically significant, but this overestimation could be problematic if you ignore the p-value and just focus on estimation."

D. Lakens, n.d.

One-Way ANOVA

Velikost účinku

library(lsr)

etaSquared(Factorial_ANOVA, type = 2, anova = FALSE)

library(sjstats)

Factorial_ANOVA2 = lm(errors ~ conversation2 * driving2, data = FANOVA)

r2(Factorial_ANOVA2, n = NULL)

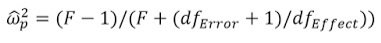
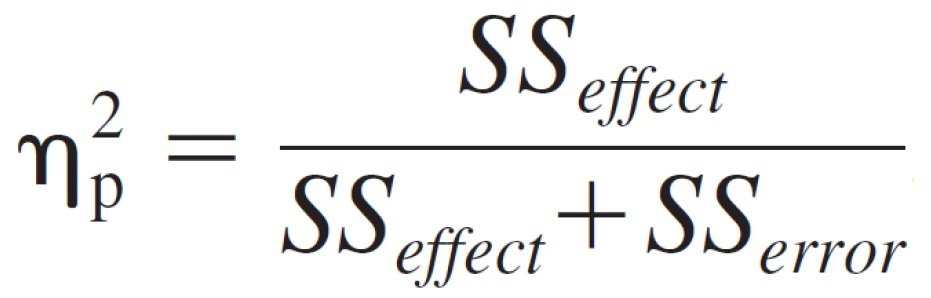
Faktoriální ANOVA

Předpoklady použití

Povaha proměnných

• "Závislá" proměnná kardinální úrovně měření

 

Normalita rozložení závislé proměnné

• V rámci každé sledované skupiny
• Narušení nepředstavuje závažný problém, pokud jsou skupiny stejně velké + mají velikost alespoň okolo 30
• Neparametrická alternativa – Kruskal-Wallisův test

 

Homogenita rozptylu

• Sledujeme Levenův F-test, nulová hypotéza hovoří o homogenitě napříč skupinami
  • Pokud Levenův F-test vychází statisticky signifikantní:
• Sledujeme poměr rozptylu u skupin s největším a nejmenším rozptylem, přičemž chceme, aby byl tento poměr menší než 3
• Narušení by nemělo vadit, pokud jsou skupiny stejně velké
• Při narušení lze použít Welchovo F

​

Nezávislost pozorování

 

Dostatečný počet případů pro každou kombinaci faktorů

Faktoriální ANOVA

Předpoklady použití

# Levene's test
leveneTest(errors ~ driving2, data = FANOVA)
# Levene's test with center = mean
leveneTest(errors ~ conversation2, data = FANOVA)

 

# Normalita rozložení

ggplot(data=FANOVA, aes(FANOVA$errors)) +
  geom_histogram(breaks=seq(0, 20, by = 2),
                 col="red",
                 aes(fill=..count..)) +
  scale_fill_gradient("Count", low = "blue", high = "purple")+
  labs(title="Errors done while driving") +
  labs(x="Errors done while driving", y="Count") + theme(legend.position='none')

Faktoriální ANOVA

Post-Hoc testy

tukey <- TukeyHSD(Factorial_ANOVA)

 

pairwise.t.test(FANOVA$errors, FANOVA$conversation2, p.adjust = "bonferroni")
pairwise.t.test(FANOVA$errors, FANOVA$driving2, p.adjust = "bonferroni")

 

Faktoriální ANOVA

Kontrasty

options(contrasts = c("contr.helmert", "contr.poly"))

contrasts(ANOVA$condition2) <- "contr.helmert"
model1 <- lm(iq ~ condition2, data = ANOVA)
summary(model1)

Základní literatura

Field, A., Miles, J., & Field, Z. (2012). Discovering Statistics Using R. Sage: UK.

 

Navarro, D. J. (2014). Learning statistics with R: A tutorial for psychology students and other beginners. Available online: http://health.adelaide.edu.au/psychology/ccs/teaching/lsr/