WE ARE COMPUTERS
What is programming?
The answer is...
3
Back to the 1930s
Alonzo Church
Alan Turing
1903 - 1995
1912 - 1954


Back to the 1930s
Computability Thesis
Any real-world computation can be translated into an equivalent computation involving a
Turing machine or lambda calculus





Lambda Calculus

Lambda Calculus
variable
abstraction
application
α-conversion
(λx.xx)(λx.x)
↓
(λx.xx)(λy.y)
β-reduction
((λx.xy) z) →
zy
((λn.n × 2) 7) →
7 × 2
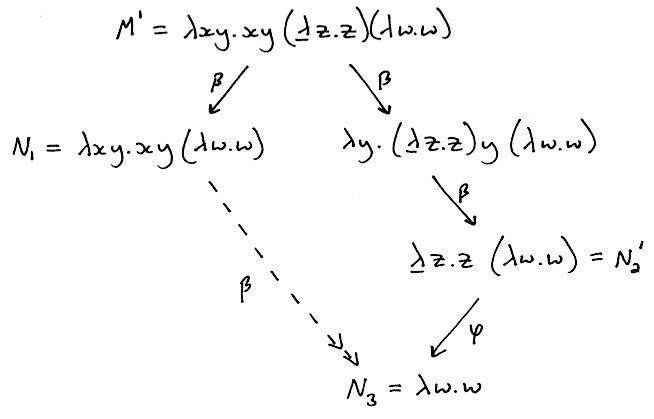
Lambda Calculus
(λx.x)((λx.λy.x y)(λy.y)(λz.z))
(λx.x)((λa.λb.a b)(λy.y)(λz.z))
(λx.x)((λb.λy.y b)(λz.z))
(λx.x)((λy.y λz.z))
(λy.y λz.z)
λz.z
Lambda Calculus
Booleans
Numbers
Strings
Arrays
Objects
Operators
3
Variables
Abstractions
Applications
Turing Complete
In computability theory, a system of data-manipulation rules (such as a computer's instruction set, a programming language, or a cellular automaton) is said to be Turing complete or computationally universal if it can be used to simulate any Turing machine.
A system in which a program can be written that will solve any computation problem
And now for a practical but not really practical example...
FizzBuzz
Write a program that prints the numbers from 1 to 100. But for multiples of three print “Fizz” instead of the number and for the multiples of five print “Buzz”. For numbers which are multiples of both three and five print “FizzBuzz”.
The FizzBuzz Problem
The FizzBuzz Problem
(n => {
(function fizzbuzz(i) {
const [f, b] = ['Fizz', 'Buzz'];
const d3 = i % 3 ? 0 : f;
const d5 = i % 5 ? 0 : b;
const d15 = d3 && d5 ? f + b : 0;
console.log(d15 || d3 || d5 || i);
if (i !== n) fizzbuzz(++i);
})(1);
})(100);The FizzBuzz Problem
Operators
Numbers
Math
Arrays
Strings
Recursion
The FizzBuzz Problem
Historical Trivia
Back during the time of Church and Turing, "Computer" meant the person who manually computes programs (not the machines).
Conditional & Logical Operators
λx.λy.x
λx.λy.y
λx.x
→ x
true
false
condition
identity
→ y
→ x
→
→
→
Conditional & Logical Operators
λx.λy.(x y false)
λx.λy.(x true y)
λf.x.y.(f y x)
and
→
→
→
or
not
Numbers
λf.λx.x
λf.λx.(f x)
λf.x.(f (f x))
0
→
→
→
1
2
λf.x.(f (f (f x)))
→
3
The FizzBuzz Problem
The Y Combinator

The Y Combinator
The Y Combinator
A higher-order function that takes a single argument, a non-recursive function, and returns a version of that function which is recursive.
The Y Combinator
The Y Combinator
The Z Combinator
λf.(λx.f (λy. x x y)) (λx.f (λy. x x y))
The Z Combinator
The FizzBuzz Problem
Resources
We Are Computers
By webguyian
We Are Computers
Solving problems in JavaScript without JavaScript
- 476



