Point Slope Form
\pi \cdot \pi
\pi \cdot \pi
\(x\)
\(y\)
\pi \cdot \pi
\((x_1, y_1)\)
\(x\)
\(y\)
\(x_1\)
\(y_1\)
\pi \cdot \pi
\((x, y)\)
\((x_1, y_1)\)
\(x\)
\(y\)
\(x\)
\(x_1\)
\(y_1\)
\(y\)
Slope of line, \(\displaystyle m=\frac{y-y_1}{x-x_1}\)
\pi \cdot \pi
Slope of line, \(\displaystyle m=\frac{y-y_1}{x-x_1}\)
Multiplying both sides by \(x-x_1\), we get:
\(\displaystyle m\cdot (x-x_1)=\frac{y-y_1}{x-x_1}\cdot (x-x_1)\)
\pi \cdot \pi
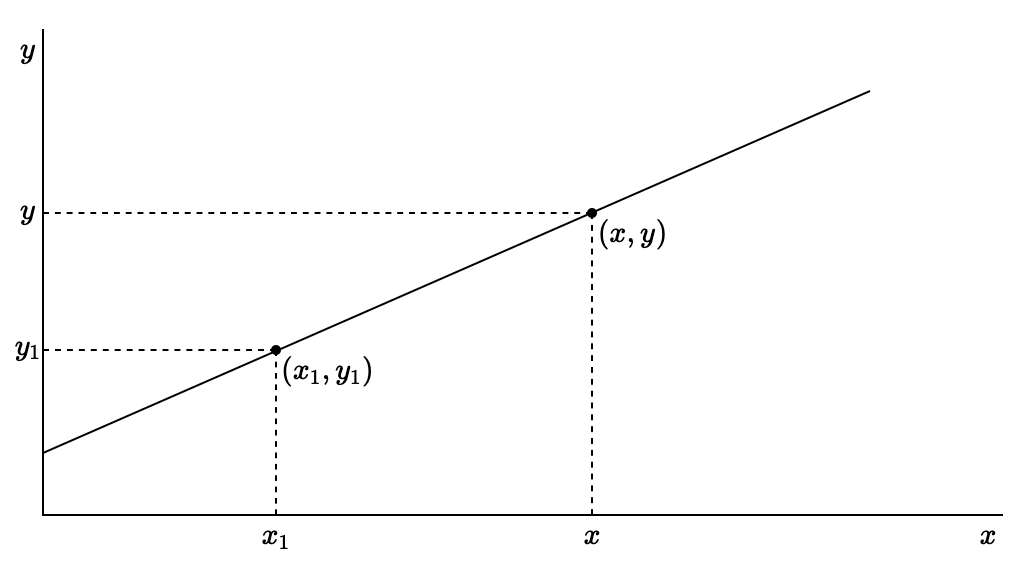
Slope of line, \(\displaystyle m=\frac{y-y_1}{x-x_1}\)
Multiplying both sides by \(x-x_1\), we get:
\(\displaystyle m\cdot (x-x_1)=\frac{y-y_1}{x-x_1}\cdot (x-x_1)\)
\(\displaystyle m\cdot (x-x_1)=\frac{y-y_1}{\cancel{x-x_1}}\cdot (\cancel{x-x_1})\)
\pi \cdot \pi
Slope of line, \(\displaystyle m=\frac{y-y_1}{x-x_1}\)
Multiplying both sides by \(x-x_1\), we get:
\(\displaystyle m\cdot (x-x_1)=\frac{y-y_1}{x-x_1}\cdot (x-x_1)\)
\(\displaystyle m\cdot (x-x_1)=\frac{y-y_1}{\cancel{x-x_1}}\cdot (\cancel{x-x_1})\)
\(\displaystyle m\cdot (x-x_1)=y-y_1\)
\pi \cdot \pi
Slope of line, \(\displaystyle m=\frac{y-y_1}{x-x_1}\)
Multiplying both sides by \(x-x_1\), we get:
\(\displaystyle m\cdot (x-x_1)=\frac{y-y_1}{x-x_1}\cdot (x-x_1)\)
\(\displaystyle m\cdot (x-x_1)=\frac{y-y_1}{\cancel{x-x_1}}\cdot (\cancel{x-x_1})\)
Rewriting the equation:
\(\displaystyle m\cdot (x-x_1)=y-y_1\)
\(\displaystyle y-y_1=m\cdot (x-x_1)\) or \(\displaystyle y-y_1=m(x-x_1)\)
\pi \cdot \pi
Point Slope Form
By Anurag Katyal
