Random Movement of Particles in Different Dimensions
Group 12
B06902029 裴梧鈞
B06902093 王彥仁
B06902097 楊皓丞
1D-Number Line
Random Walk
1D Random Walk
On the number line, we set the ball on the origin x = 0, during each time interval dt, the ball can move to the adjacent two position, which are x-1, x+1, with the equal probability.
For simplicity, we set dt = 1, T_max = 500
1D Random Walk
As we test the program many times, we find that the average distance from origin to time will be like a square root graph.
We test 1000 times to get the average.
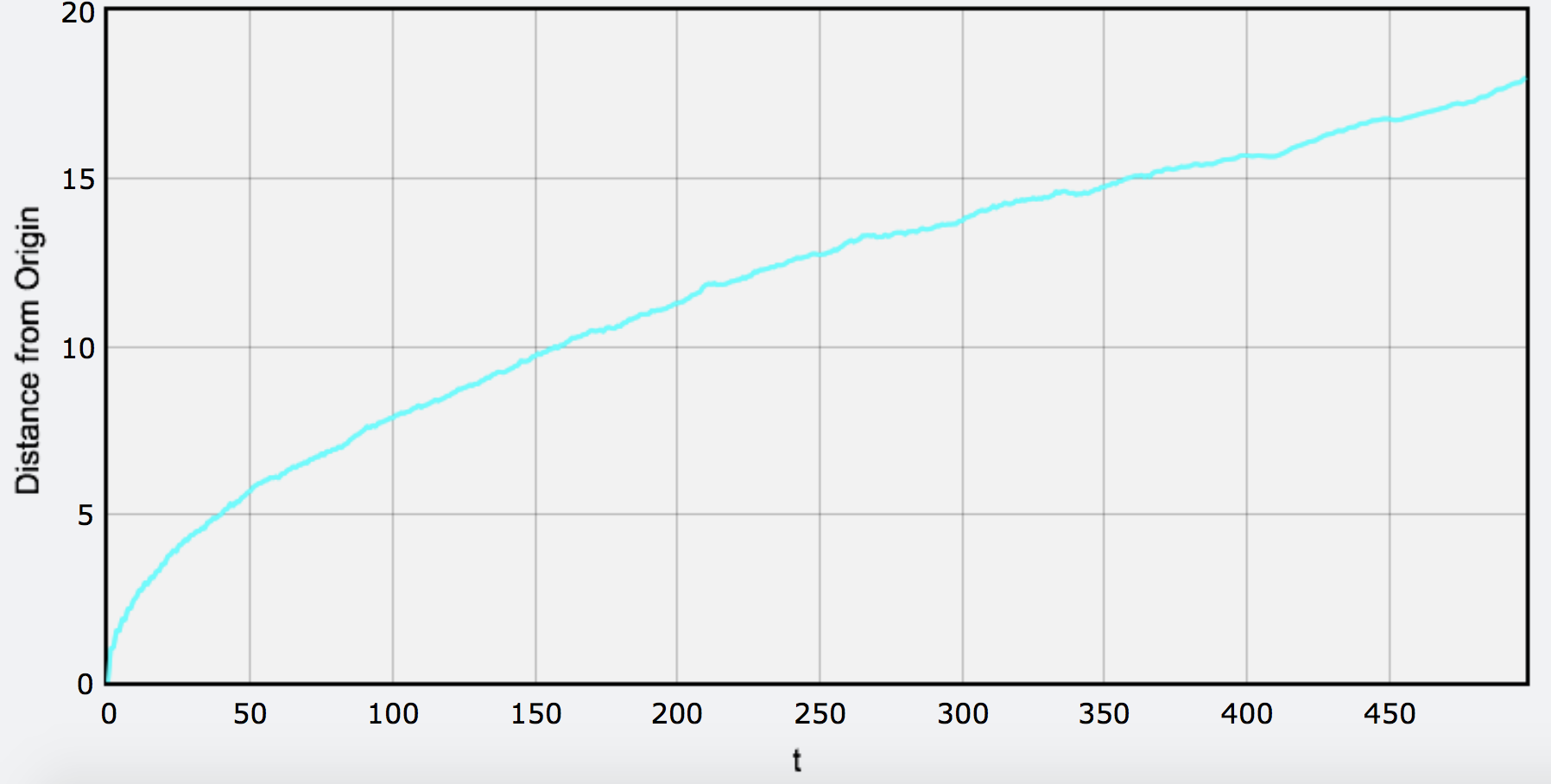
1D Random Walk
We find the coefficient of sqrt( t ) is 0.8070 by observation. After wikiing, we find the coefficient is
E( t ) = \sqrt\frac{ 2 }{ \pi } * \sqrt{ t }
\sqrt\frac{ 2 }{ \pi }
1D Random Walk
Yellow: y = \sqrt{ \frac{2}{ \pi } } * \sqrt{t}
Cyan: y = avg( E( t ) )
Application
The model of random walk is useful to predict random behavior. The 1D model of random walk gives us an insight and a comparison as we head on to 2D and 3D.
2D-Number Plane
Random Walk
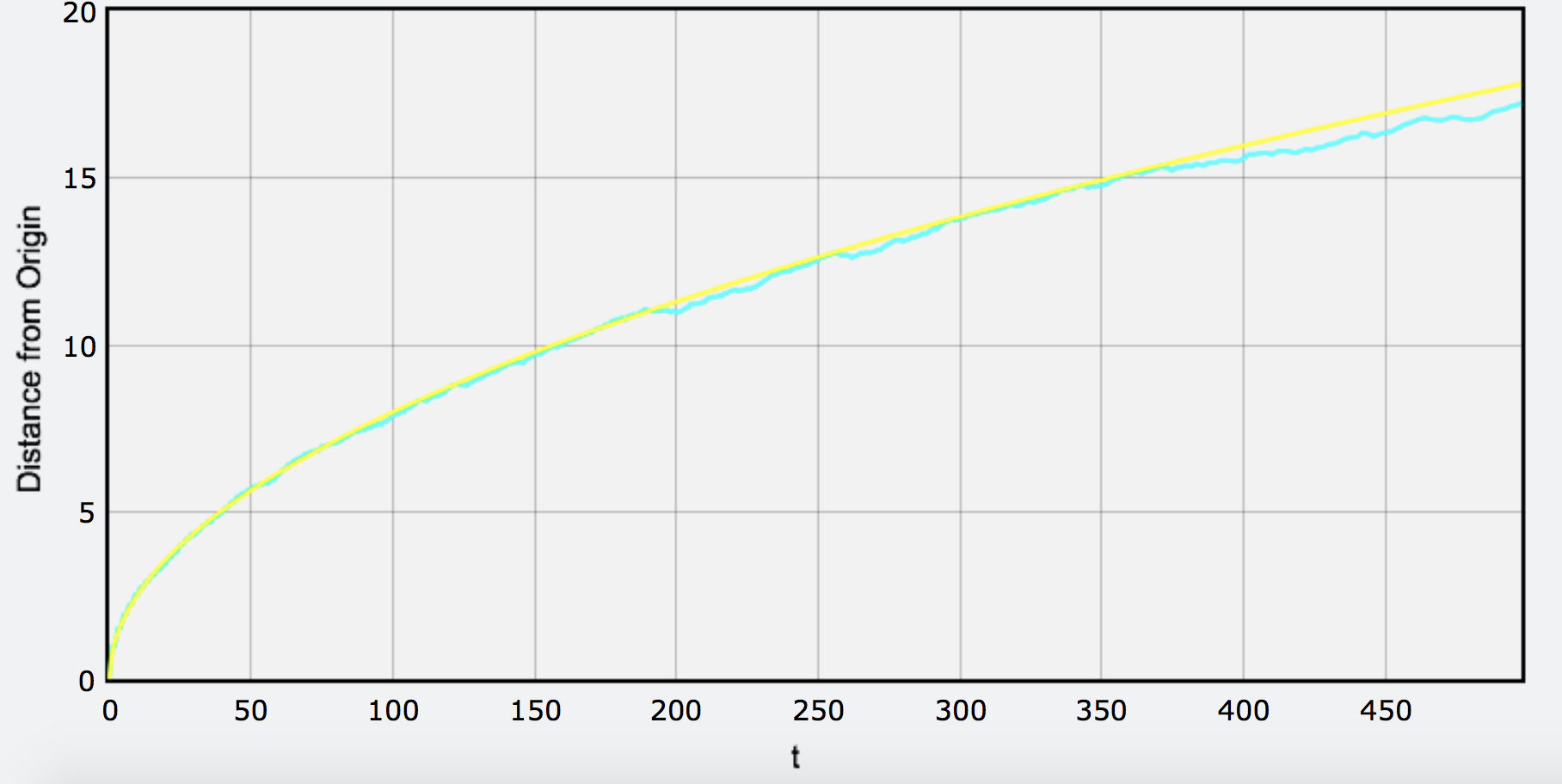
Result
Nice! It looks like a square root function and the coefficient is roughly 0.79, which corresponds to the actual solution
\sqrt\frac{ \pi }{ 4 }
Application
- Effective expected range of a lost person
- Random 2D movement... Brownian motion?
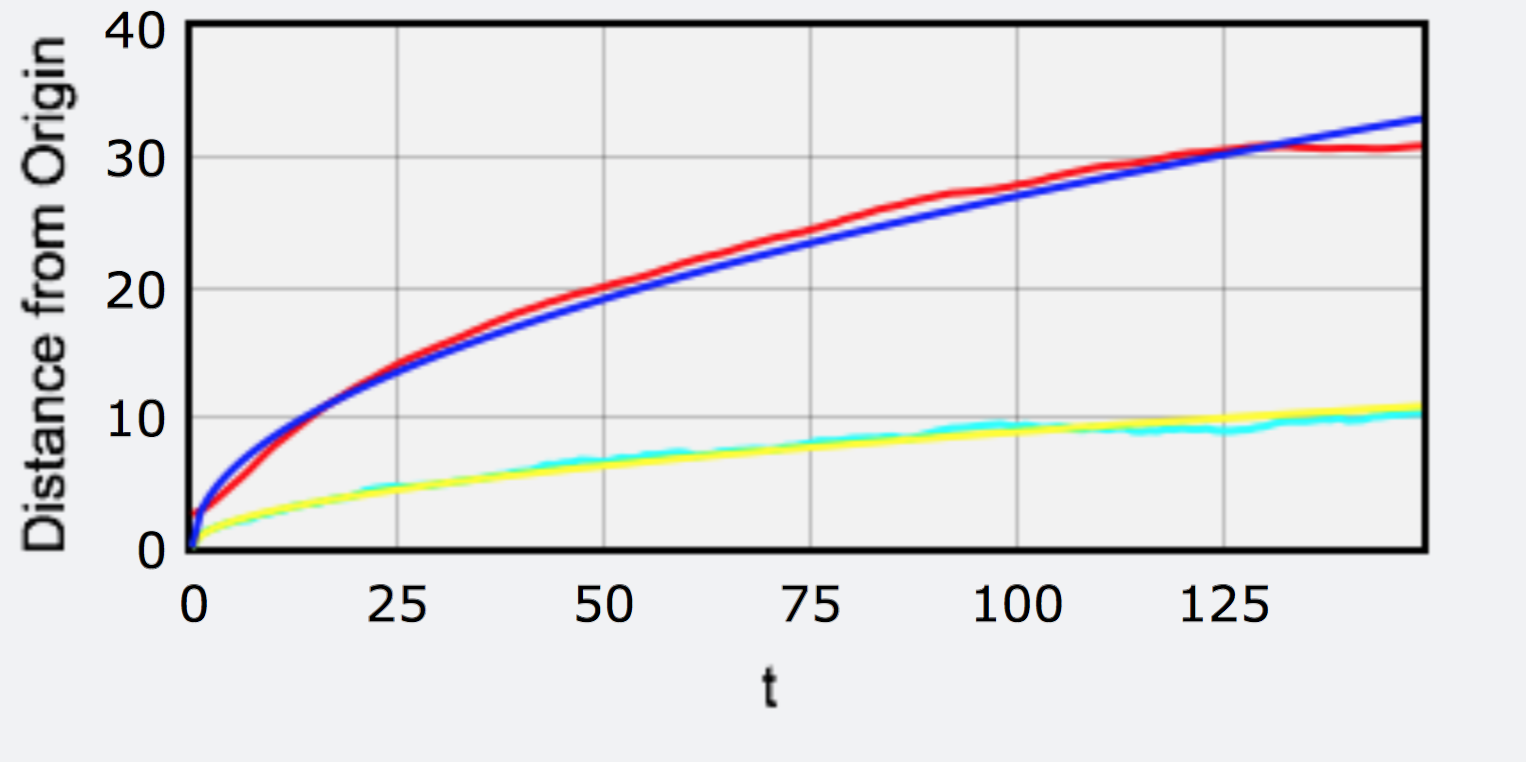
Brownian motion seems random but it is actually particle collisions. We can't be sure they are identical. Therefore, we simulated the collision of particles in 2D plane.
2D-Number Plane
Particle Collision
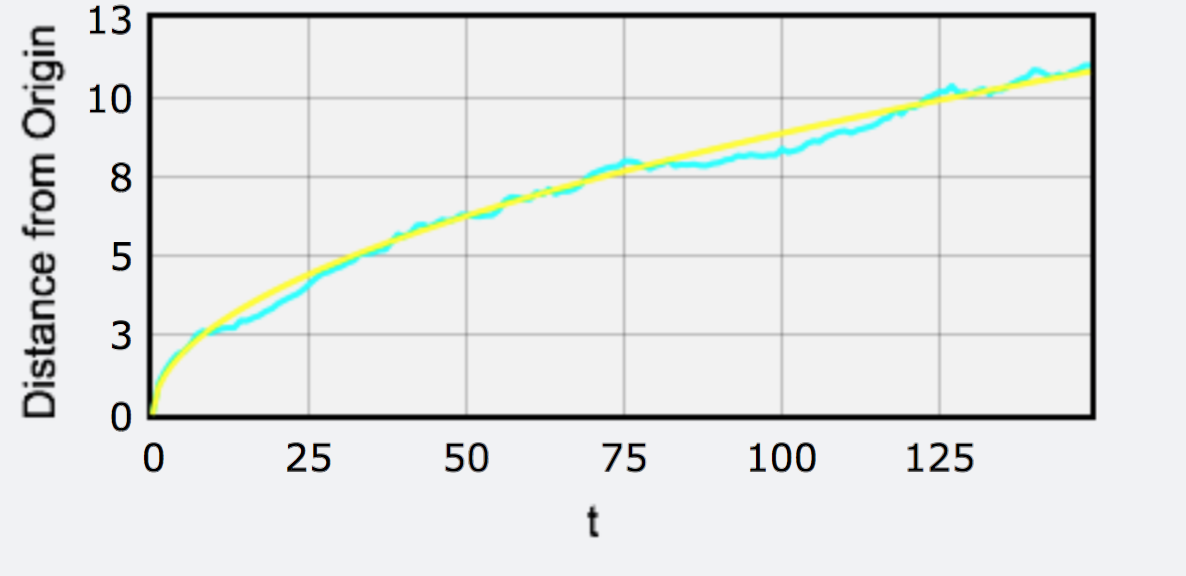
Results
Wow! In particle collision, the distance from origin respect to time is also a square root function!
Applications
- We just simulated the Brownian motion, and the graph shows that it can be modeled into a square root function too, the coefficient should be related to the density of the particles.
- That means random walk could be used to explain and predict Brownian motion or other random collision in the 2D plane.
- How about in 3D space?
3D-Number Space
Random Walk
Result
After running 3D random walk many times, we plot the average graph - the distance from origin of time. We can see that it looks like a square root function easily! It corresponds to the actual solution
\sqrt\frac{ 8 }{ 3\pi }
{\displaystyle \Gamma (z)=\int _{0}^{\infty }x^{z-1}e^{-x}\,dx}
E( t ) = \sqrt{ \frac{ 2t }{ d } } \frac{ \displaystyle \Gamma ( \frac{ d + 1 }{ 2 } ) }{ \displaystyle \Gamma ( \frac{ d }{ 2 } ) }
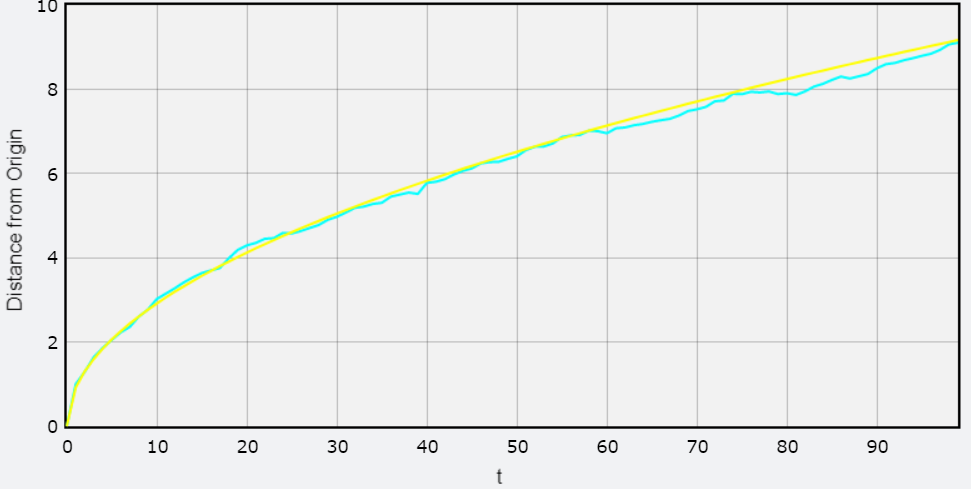
Where t is the time, and d is the dimension.
3D-Number Space
Particle Collision
Results
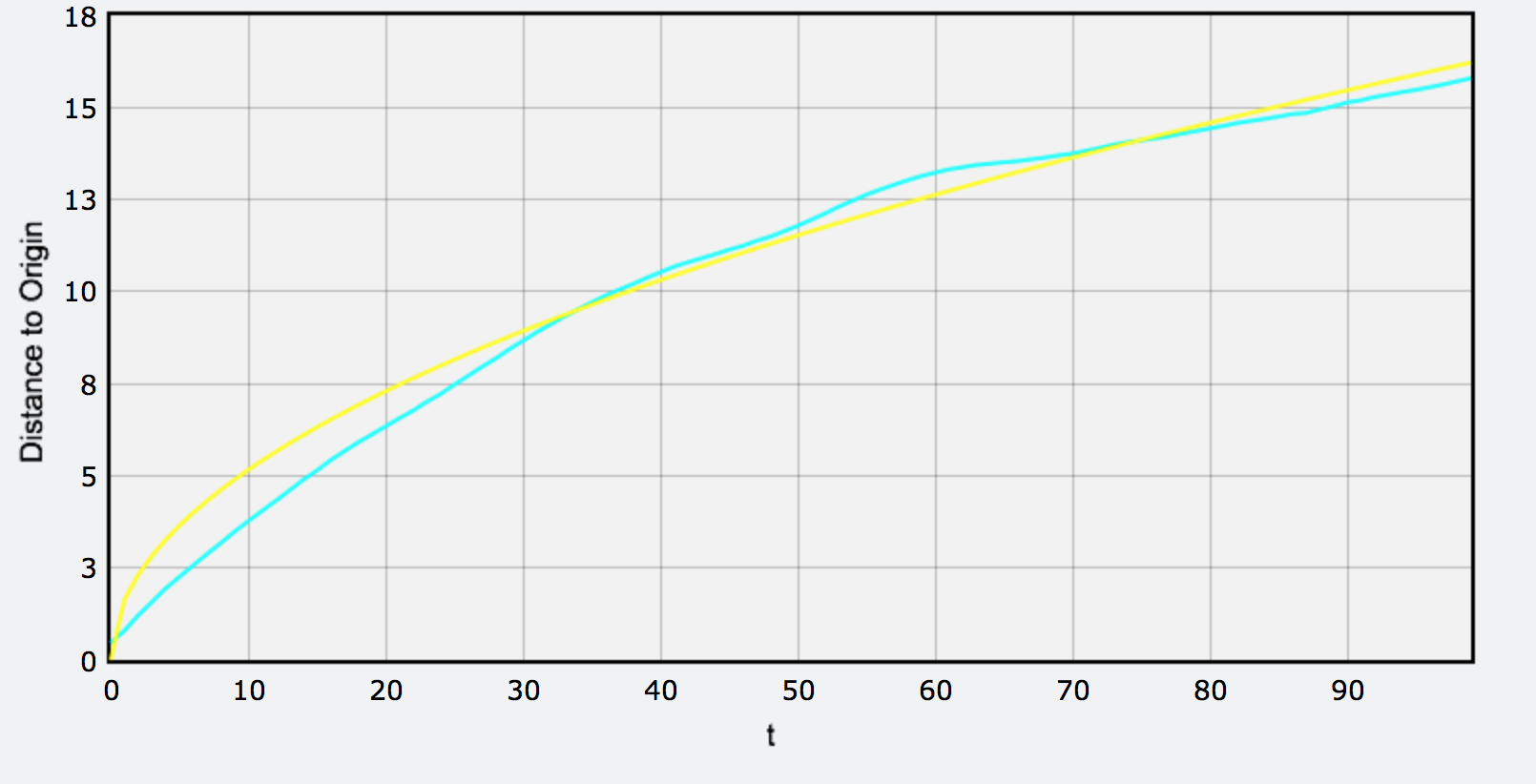
After conquering tremendous difficulties, we finally acquired a nice graph. It is still a square root function! The coefficient is about 1.65
Applications
- 3D Particle Collision - Particle Diffusion
- Gas and liquid diffusion is particle collision in the 3D space, it is often hard to predict or calculate the behaviors since it involves too many interacting objects. However, our results show that we can instead just use the random walk model!
- The square root identity we observed can actually be seen in the Fick's law.
Fick's Law
n\left(x,t \right)=n(0) \left( 1 - 2 \left(\frac{x}{2\sqrt{Dt\pi}}\right) \right)
This is the 1D formula of the Fick's Law where n represents the concentration. The term is called the diffusion length.
It showed the same square root term as seen in random walk.
2\sqrt{Dt}
Applications
- Demo of particle diffusion effect!
- Real life examples:
- Liquid: Dripping a drop of ink into a glass of water
- Gas: The spread of farting in the classroom
Conclusion
When the density of particles is high enough, the collision of the particles seemed that it's random. In fact, through our project, we confirmed that the movements of random walk and particle collision are actually almost identical. Therefore, the model of random walk can be used to explain particle collisions in every dimension.
And the important square root identity holds throughout our experiments.
Reference
1. Brownian Motion (Wikipedia)
2. Kinetic Theory of Gases (Wikipedia)
3. Random Walk (Wikipedia)
4. Expected Value of Random Walk (StackExchange)
5. Fick's laws of diffusion (Wikipedia)
[GP17] Group12
By Wu-Jun Pei
