The role of filament recycling in stable flows of 2D active networks
Committee meeting
William McFadden 2016
How to change your own shape
how can an organism rearrange itself internally and externally?
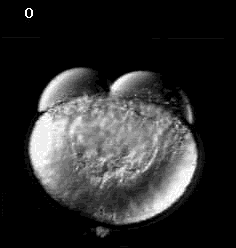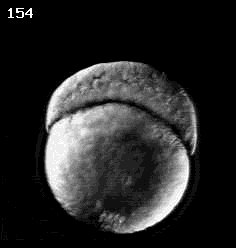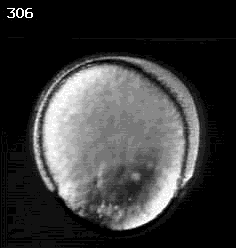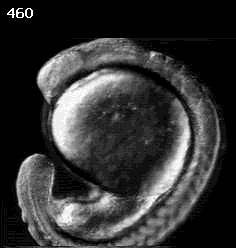
Don Kane (U. Rochester)
Cellular processes are the drivers of macroscopic reorganization
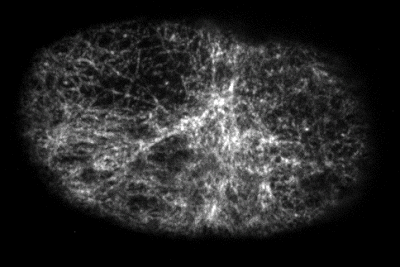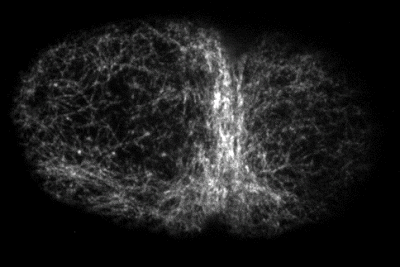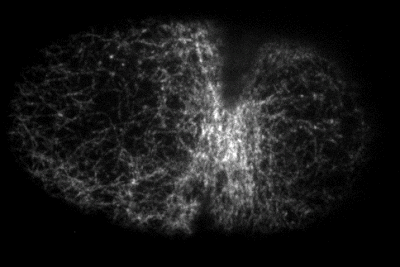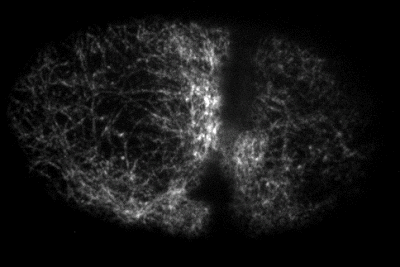
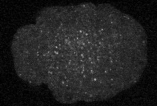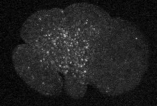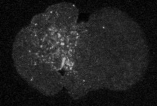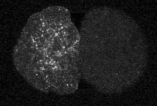
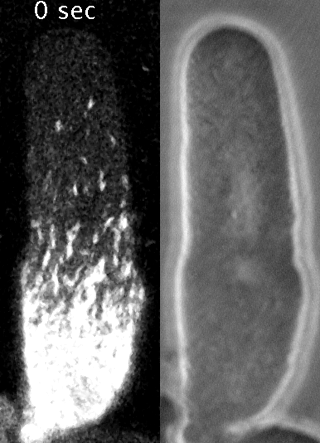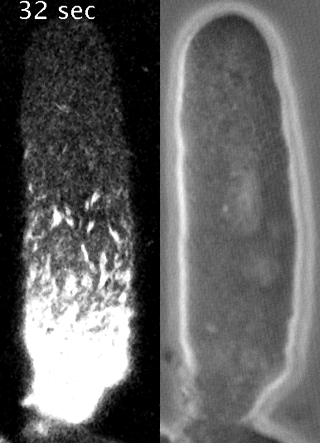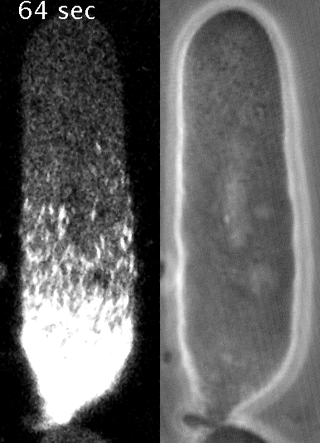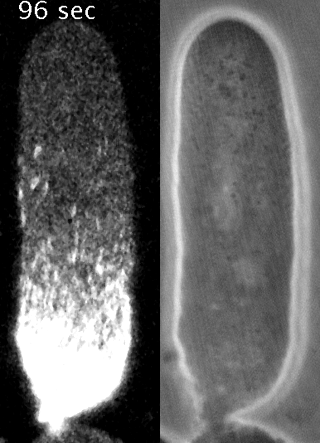
Yumura et al. 2013
ed munro
crawling
division
polarization
cellular reorganization via cortical flows
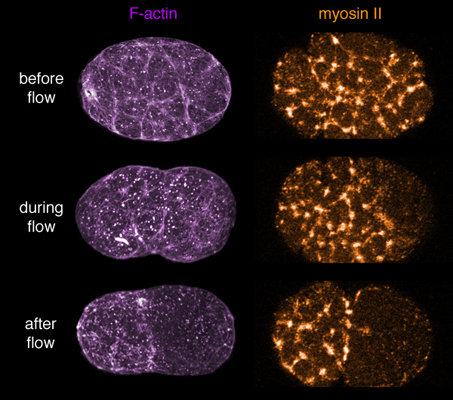
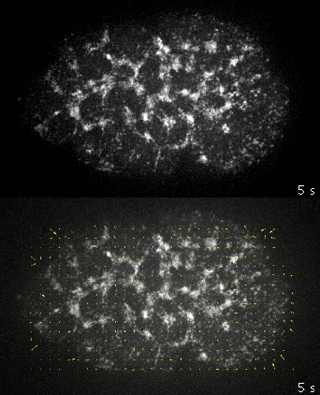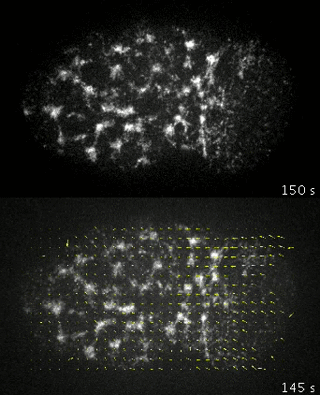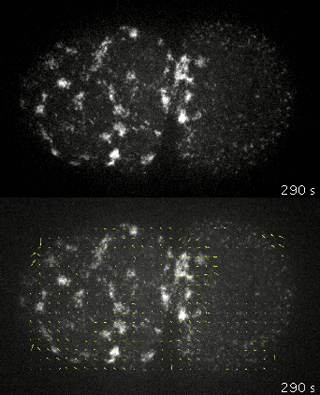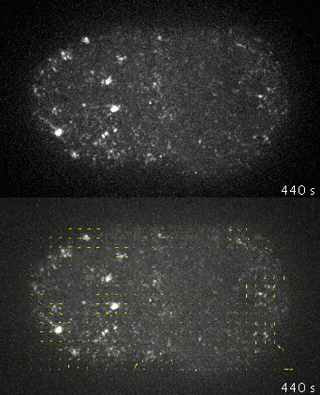
Mmayer et al. 2010
ed munro
flows of cortical actomyosin cytoskeleton
actin filaments
and myosin motors
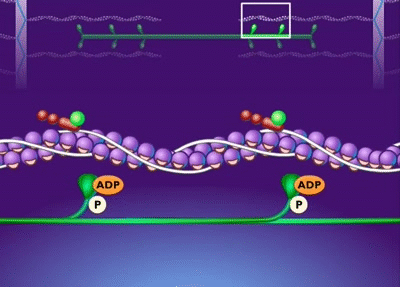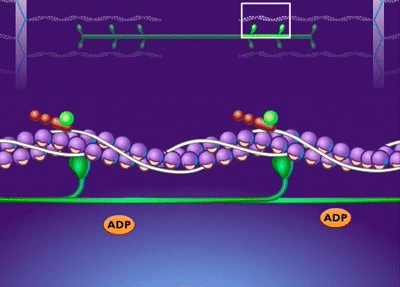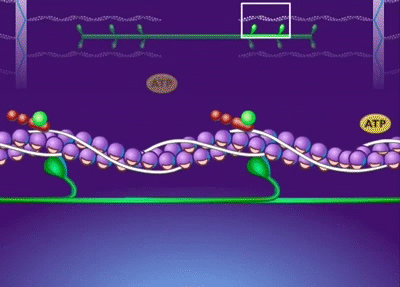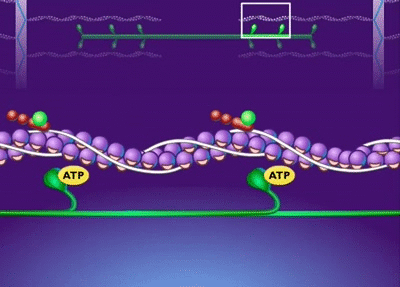

2D disordered network


flows of cortical actomyosin cytoskeleton
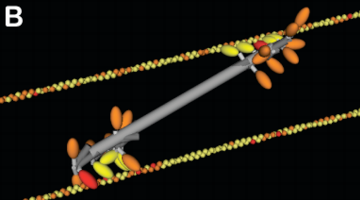
Actomyosin networks generate forces and spontaneously deform
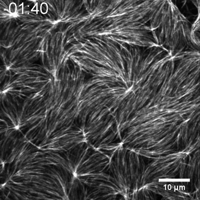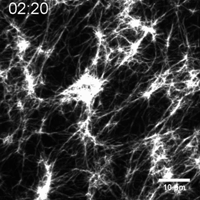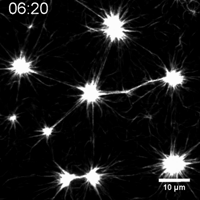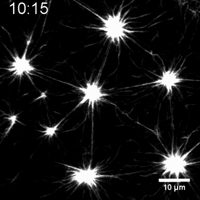
Murrell and Gardel 2012
flow is driven by internal force imbalances
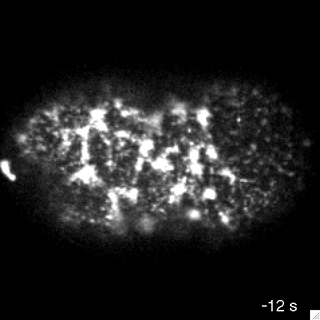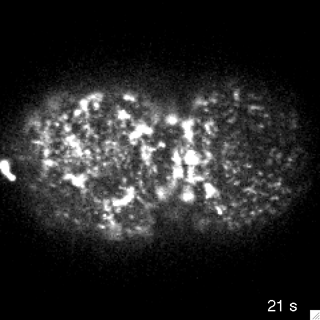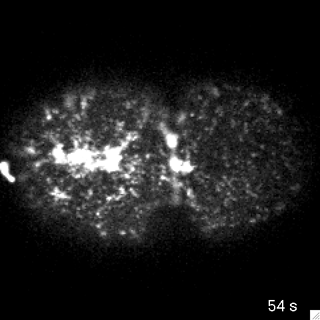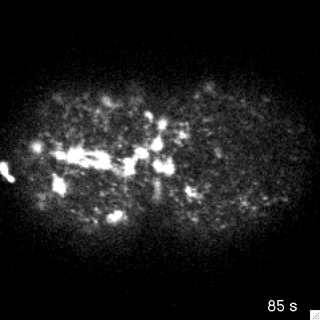
Passive
Active
Mayer et al. 2010
filament recycling: key to sustaining flows
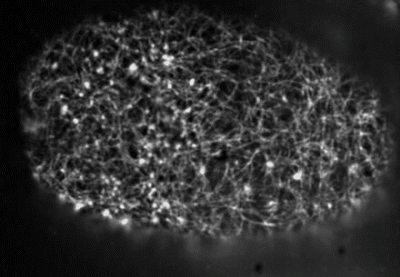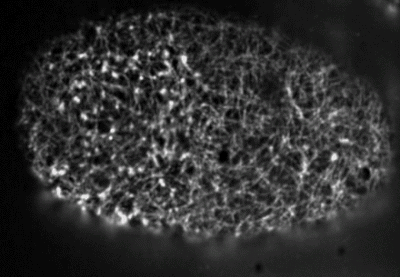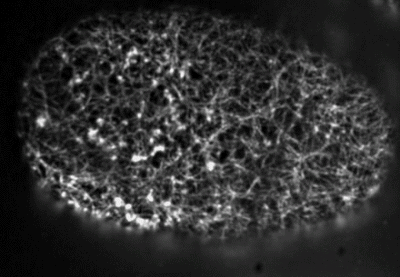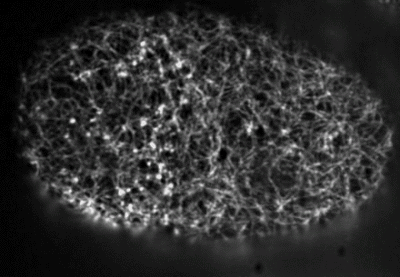
F-actin filaments are highly dynamic
cellular mechanisms of filament recycling
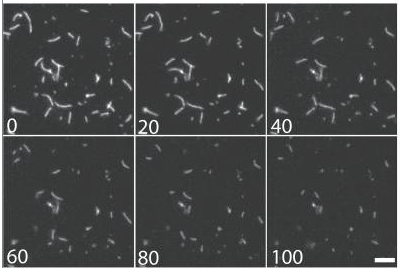

disassembly takes places in 100 s
Kuey et al. JCB 2008
in vivo, the lifetime can be even shorter
during division
pre-division
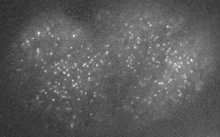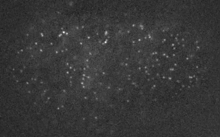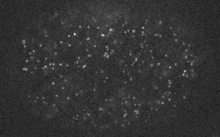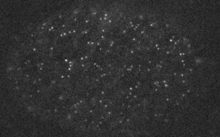
Robin et al. 2012
Preventing filament recycling stalls flows or leads to cortical tearing
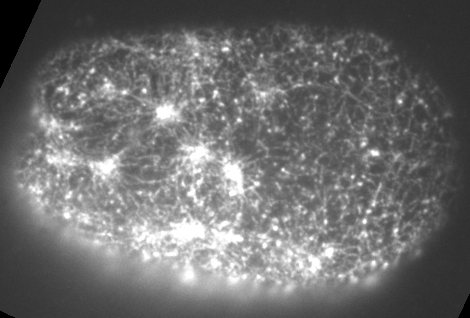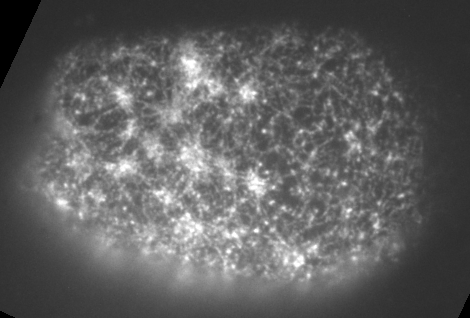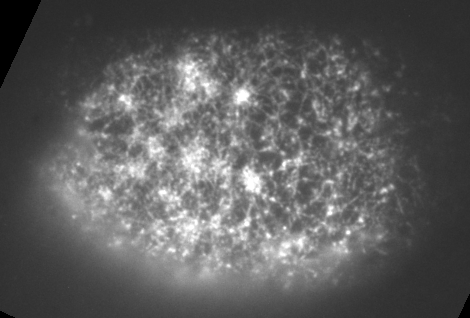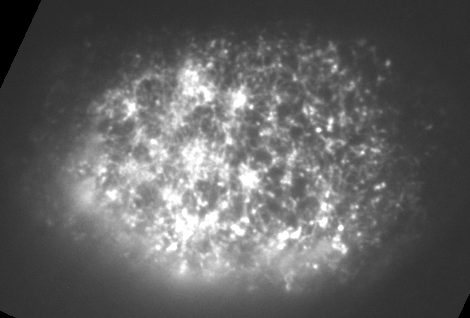
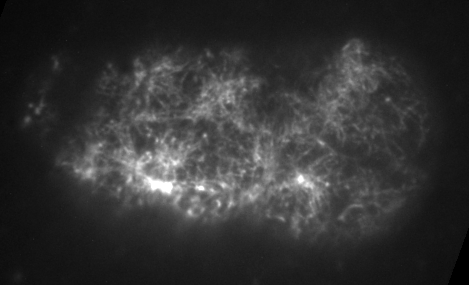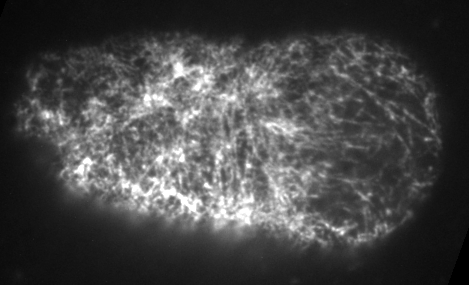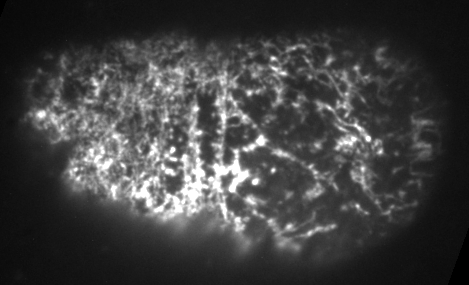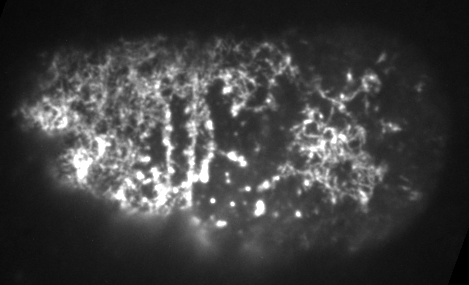
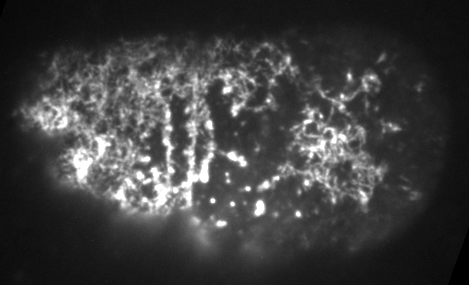
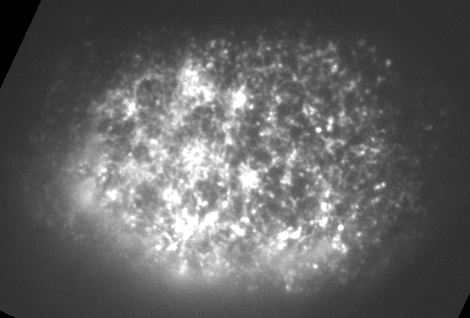



Jon Michaux
japlakinolide
goal: understand what sets flow rate
Passive
Active
stress
viscosity
approach: determine what sets network viscosity and internal stress
Probing passive viscosity of 2D filament networks in presence of applied force
frictional cross-link stress dissipation




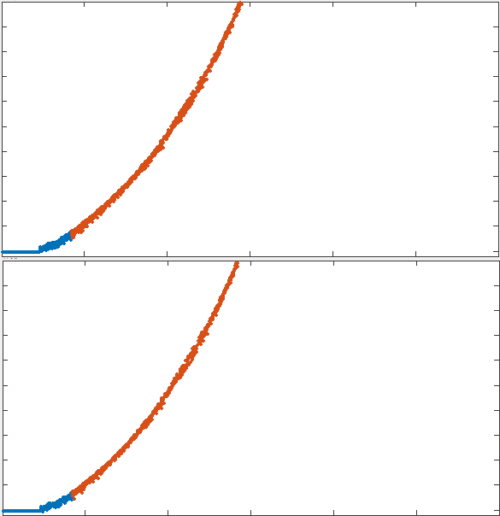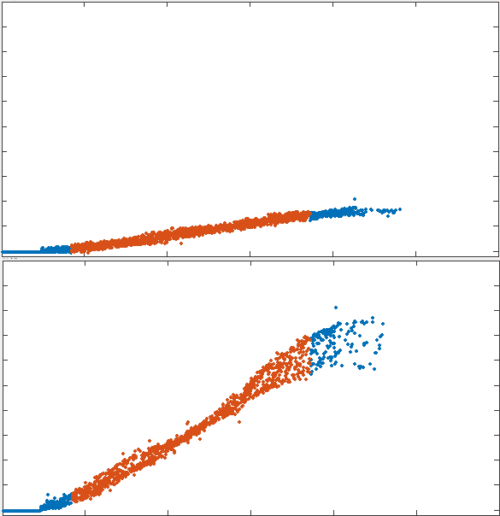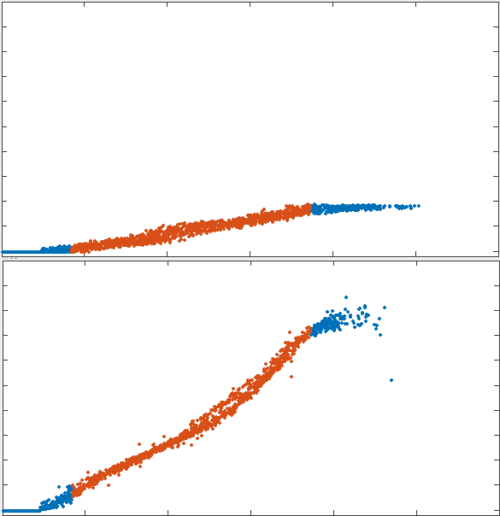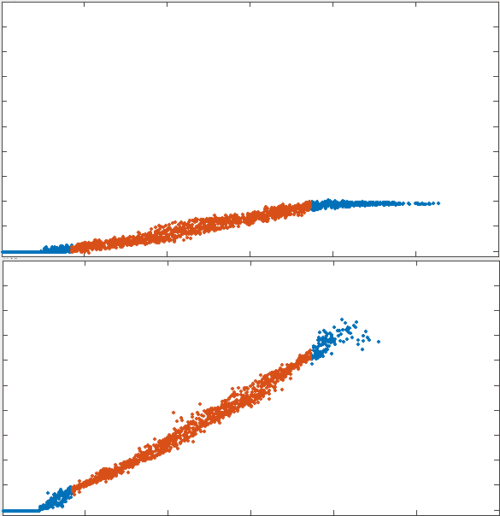
measuring passive network deformation


position
x velocity
This led to typical 3 phase deformation


\tau_c
τc
1/\eta
1/η
G_0
G0
G0 agrees with prior theoretical prediction

Head Levine Mackintosh, PRL 2003
estimate of viscosity of networks with cross-link relaxation


\tau_c
τc
1/\eta
1/η
what happens when we introduce highly simplified filament recycling?

filament recycling led to faster strains

position
x velocity
x velocity
no recycling
tau = 10s
Only with fast enough recycling, the network's effective viscosity decreased


\tau_x \approx 100\tau_c
τx≈100τc
Measuring deformation and stress buildup in 2D active filament networks
build a minimal model of active networks




asymmetric filament compliance

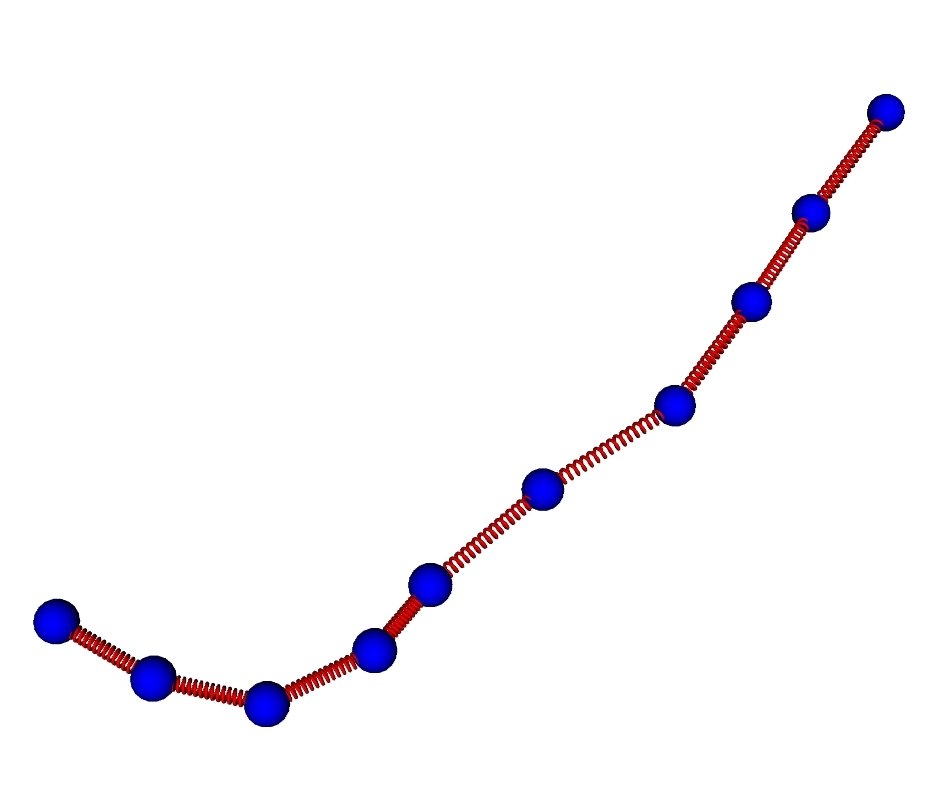

L
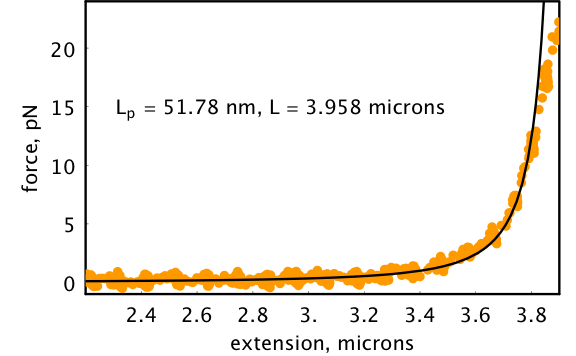
Storm and Nelson PRE 2003
Active networks transiently contract



free boundary
and generate a transient net stress



fixed boundary
\tau_a
τa
recycling tunes the steady state stress


\tau_a
τa
biphasic dependence on recycling time



Combining passive viscosity and active stress to predict 1D flows
recap: estimates for stress and viscosity


recall the dependence on these two important timescales
equations for viscosity and stress can be combined to predict flow speed

\dot{\gamma}=\frac{\sigma}{\eta}
γ˙=ησ
strain rate
viscosity
stress
to test our theory we generated simulations of polarized networks

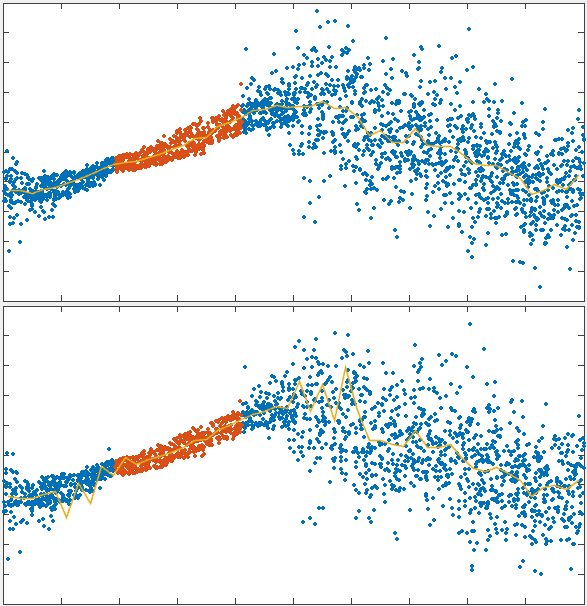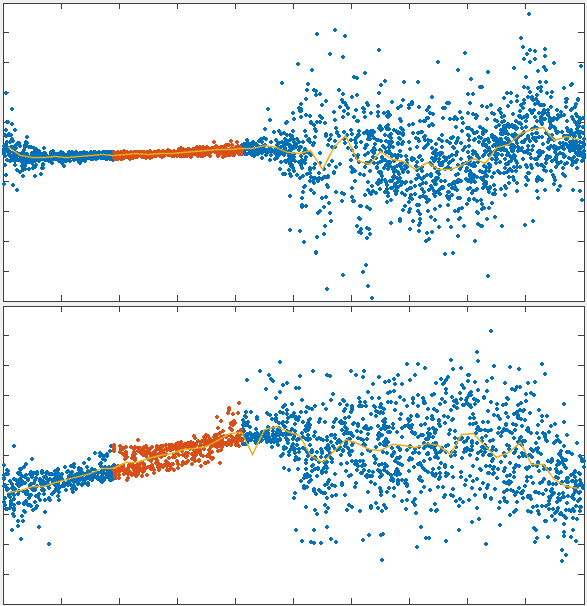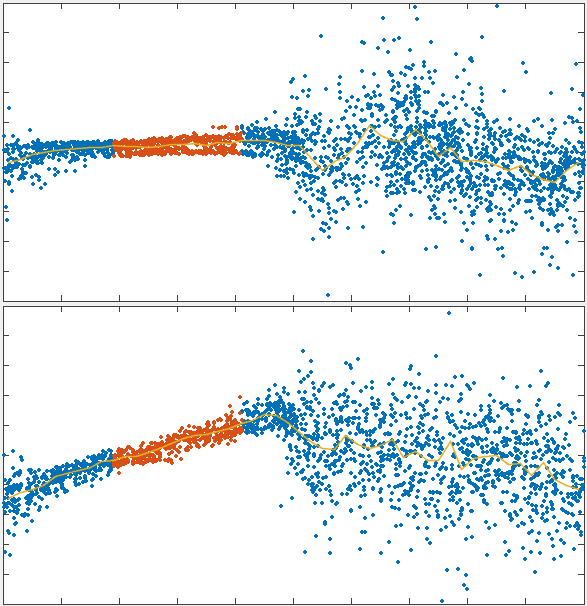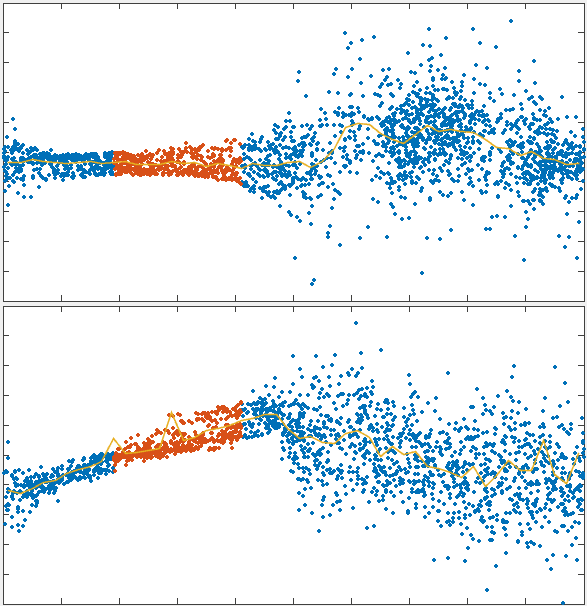
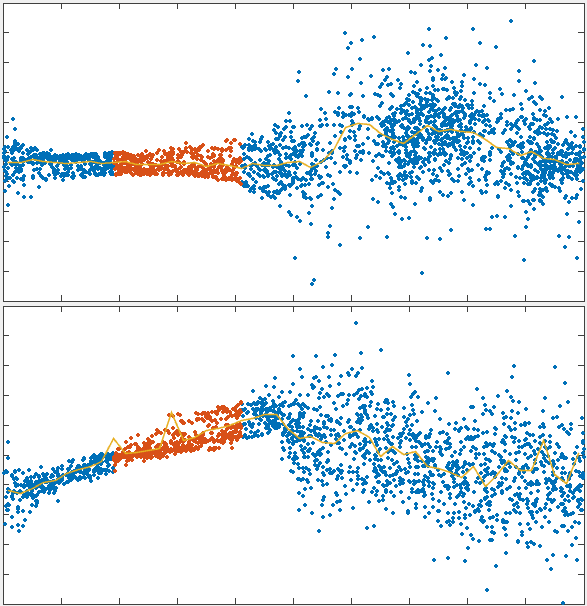
x velocity
x velocity
position
1000s
\tau_r
τr
33s
active region
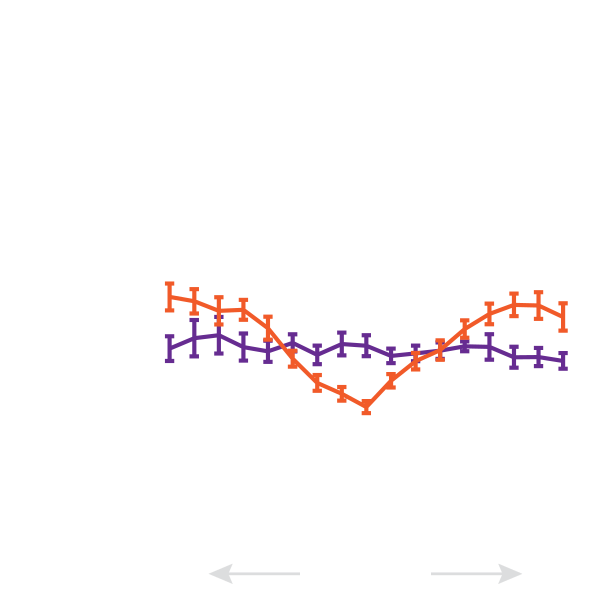
charting steady state flow dependence on recycling timescale





dependence of flow speed on recycling qualitatively matches theoretical prediction
flow simulations recapitulated the predicted interplay of these two effects





inert
tearing
conclusions and future directions
this work offers a theoretical framework for understanding cortical flows
it sets up some experiments to test both quantitative and qualitative predictions
it might help explain what needs to be controlled to generate synthetic systems
a theoretical framework
is "X experiment" important for tuning actomyosin flow?



experimental tests




synthetic systems







theseus old
By wmcfadd2
theseus old
- 937
