算法概念与性能分析

什么是算法？

请输入两个数字X和Y，计算两个数的和

在这个例子当中，如果我们要完成这个功能，我们需要经过那些步骤？

输入X和Y的值
计算X+Y的结果
输出最后的结果

三个步骤

其实算法就是解决问题的一系列方法和步骤

例如：刚才的三个步骤就是解决X+Y这个问题的算法，一系列的步骤，当然，我们演示的这个算法很简单，但是真正的算法都是非常复杂的

算法的作用

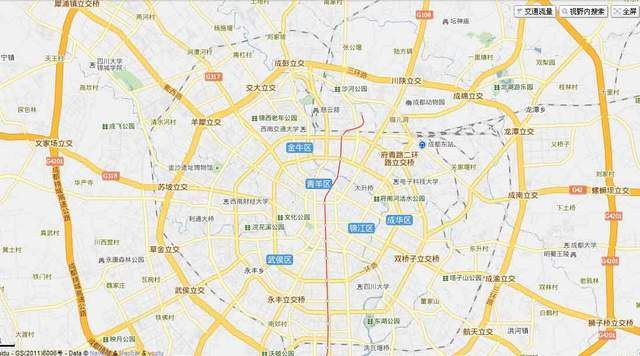
在交通导航的运用中，软件是如何实现挑选路径的呢？就是通过算法来实现，通过算法，实现找到两个位置的最短路径，以便使用者可以快速到达目的的

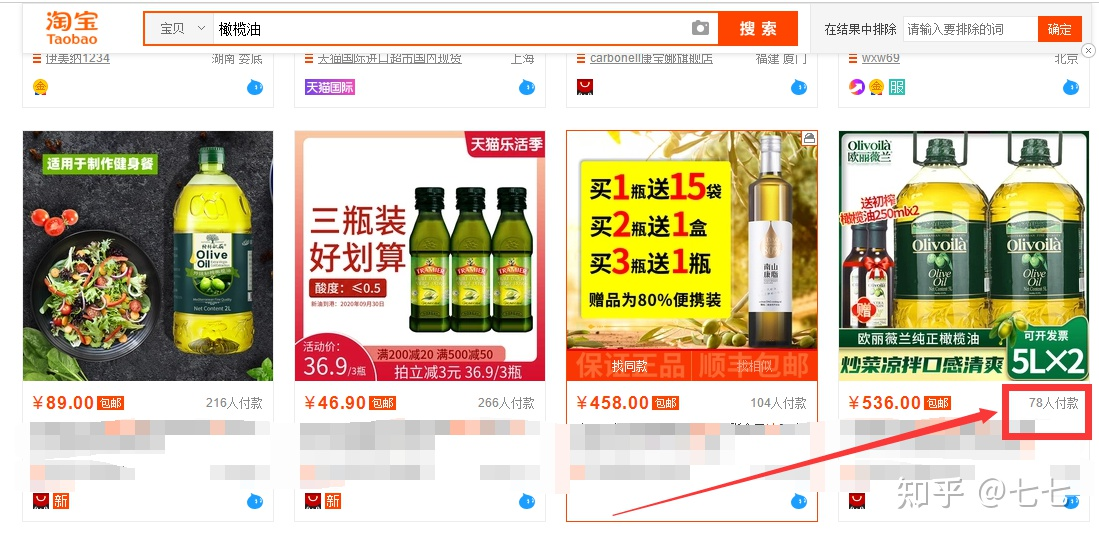
在使用淘宝的过程当中，淘宝会自动记录我们浏览过那些商品，并且在之后为我们推荐相似的商品出来，这也是算法的应用之一。

算法的性能

对于一个算法来说，非常重要的就是在保证算法的正确的前提下去衡量这个算法的性能，主要从两个方面来衡量

时间：这个算法运行完成之后，需要花费多长的时间
空间：实现这个算法，需要消耗多少内存空间

对于空间消耗来说，随着科学技术的不断发展，我们的内存空间也越来越大，因此在空间上，是可以保证这个算法的运行内存的

时间是一个重要的考量因素，对于人类来说，时间是非常宝贵的，我们没有这么多的时间去等待一个算法运行完成，因此，对于一个算法来说，时间是最首要的考量因素

为了更加准确的去衡量时间，我们使用时间复杂度的概念去衡量时间，并用大O的方式来表示，并计算出了几个时间复杂度级别

增长级别	符号表示
常数级别	O(1)
对数级别	O(logN)
线性级别	O(N)
线性对数级别	O(NlogN)
平方级别	O( )
立方级别	O( )
指数级别	O( )

2^N

N^3

N^2

#include <iostream>

using namespace std;

int main(){
    int sum = 0;
    
    for (int i = 1;i <= 10;i++){
        sum += i;
    }

    cout << sum << endl;
}

在这个程序当中，循环总共计算了10次，并且随着输入的增加，永远都是循环10次，因此该程序的时间复杂度是O(1)

#include <iostream>

using namespace std;

int main(){
    int sum = 0;
    int N;
    cin >> N;
    
    for (int i = 1;i <= N;i++){
        sum += i;
    }

    cout << sum << endl;
}

在这个程序当中，循环总共计算了N次，并且随着输入的增加计算的次数也会增加，因此该程序的时间复杂度是O(N)

#include <iostream>

using namespace std;

int main(){
    int sum = 0;
    int N;
    cin >> N;

    for (int i = 0;i < N;i++){
        for (int j = 0;i <N;j++){
            sum += j;
        }
    }

    cout << sum << endl;
}

在这个程序当中，外层循环总共计算了N次，内层循环总共计算了N次，总次数为N*N，并且随着输入的增加计算的次数也会增加，因此该程序的时间复杂度是O( )

N^2

C++性能测试

我们可以利用C++提供的时间函数库来测试函数的运行时间

time_t start = time(NULL)

使用time()函数获取当前时间

使用当前函数需要包含头函数<time.h>

#include <iostream>
#include <time.h>

using namespace std;

int test(int N){
    int sum = 0;
    for (int i = 0;i < N;i++){
        sum += i;
    }
    return sum;
}

int main(){
    int sum;
    time_t start,end;

    start = time(NULL); //记录开始时间

    sum = test(10);
    end = time(NULL);   //记录结束时间

    cout << "time:" << (end- sum) << endl;
}

Level3_1_算法概念与性能分析

By yang he