JavaScript函数式编程
Functional Programming in JavaScript
by StEve Young



一、什么是函数式编程?
What is FP?
Functional programming is a programming paradigm
1.treats computation as the evaluation of mathematical functions
2.avoids changing-state and mutable data
- by wikipedia
1.1.什么是编程范式?
What is Programming Paradigm?
- from Programming paradigms
编程范式从概念上来讲指的是编程的基本风格和典范模式。
——世界观和方法论。
如果把一门编程语言比作兵器,它的语法、工具和技巧等是招法,那么它采用的编程范式也就是是内功心法。
1.2.什么是数学函数?
What is Mathematical Functions?
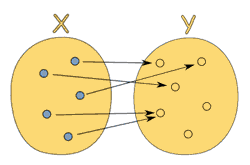
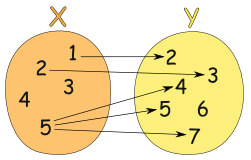
1.2.1.什么是纯函数?
What is Pure Functions?
纯函数(Pure Functions)是这样一种函数,即相同的输入,永远会得到相同的输出,而且没有任何可观察的副作用。
引用透明性(Referential Transparency)指的是,如果一段代码在不改变整个程序行为的前提下,可以替换成它执行所得的结果。
const double = x => x * 2
const addFive = x => x + 5
const num = double(addFive(10))
num === double(10 + 5)
=== double(15)
=== 15 * 2
=== 301.2.2.什么是副作用?
What is Side Effects?
副作用是在计算结果的过程中,系统状态的一种变化,或者与外部世界进行的可观察的交互。包括但不限于:
- 更改文件系统
- 往数据库插入记录
- 发送一个 http 请求
- 改变数据
- 打印/log
- 获取用户输入
- DOM 查询
- 访问系统状态
- ...
只要是跟函数外部环境发生的交互就都是副作用——这一点可能会让你怀疑无副作用编程的可行性。
函数式编程的哲学就是假定副作用是造成不正当行为的主要原因。
1.2.3.纯函数的好处都有啥?
Why Pure Functions?
面向对象语言的问题是,它们永远都要随身携带那些隐式的环境。你只需要一个香蕉,但却得到一个拿着香蕉的大猩猩...以及整个丛林
- 可缓存性(Cacheable)
- 可测试性(Testable)
- 合理性(Reasonable)
- 并行代码(Parallel Code)
- 可移植性/自文档化(Portable / Self-Documenting)
by Erlang 作者:Joe Armstrong

const obj = { val: 1 }
someFn(obj)
console.log(obj) // ??1.3.为什么要避免改变状态和可变数据?
Why avoid Changing-State and Mutable Data?
1.3.为什么要避免改变状态和可变数据?
Why avoid Changing-State and Mutable Data?
- from Shared mutable state B L
1.4.原教旨函数式 VS 温和派函数式?
Pure FP VS Impure FP?
- Haskell
- OCaml
- Lisp
- Erlang
- Scala
- F#
- ...
- JavaScript?
- 函数是“一等公民”
- 不可变数据
- 使用递归而不是循环
- 柯里化
- 惰性求值
- 代数数据类型
- 模式匹配
- ...

事实上,JavaScript 是一门基于原型(prototype-based)的多范式语言。
- 高阶函数
- 函数是一等公民
- 闭包
- 匿名函数
- 箭头函数
- 解构(模式匹配)
- ...
1.4.原教旨函数式 VS 温和派函数式?
Pure FP VS Impure FP?
1.5. 作为函数式语言 JavaScript 还差什么?
The missing things from JS for a FP?
- 不可变数据结构
- 惰性求值
- 函数组合
- 尾递归优化
- 代数类型系统

wholeNameOf(
getFirstName(),
getLastName()
)
[1, 2, 3, 4]
.map(x => x + 1)Lodash VS Underscore?

TypeScript?
二、声明式 VS 命令式
What VS How
Declarative VS Imperative
2.1.“意识形态”上的区别
The Difference In Ideology
声明式 程序抽象了控制流过程,代码描述的是 —— 数据流:即做什么。
命令式 代码描述用来达成期望结果的特定步骤 ——控制流:即如何做。
声明式 更多依赖表达式。
表达式是指一小段代码,它用来计算某个值。表达式通常是某些函数调用的复合、一些值和操作符,用来计算出结果值。
命令式 频繁使用语句。
语句是指一小段代码,它用来完成某个行为。通用的语句例子包括 for、if、switch、throw,等等……
function mysteryFn(nums) {
let squares = []
let sum = 0
for (let i = 0; i < nums.length; i++) {
squares.push(nums[i] * nums[i])
}
for (let i = 0; i < squares.length; i++) {
sum += squares[i]
}
return sum
}1. 创建中间变量
2. 循环计算平方
3. 循环累加
以上代码都是 how 而不是 what...
const mysteryFn = (nums) => nums
.map(x => x * x)
.reduce((acc, cur) => acc + cur, 0)a. 平方
2.2.举一些栗子🌰
b. 累加
Examples
例1:希望得到一个数组每个数据平方后的和
function mysteryFn(nums) {
let sum = 0
let tally = 0
for (let i = 0; i < nums.length; i++) {
if (nums[i] % 2 === 0) {
sum += nums[i] / 2
tally++
}
}
return tally === 0 ? 0 : sum / tally
}1. 创建中间变量
2. 循环,值为偶数时累加该值的一半并记录数量
3. 返回平均值
const mysteryFn = (nums) => nums
.filter(x => x % 2 === 0)
.map(x => x / 2)
.reduce((acc, cur, idx, { length }) => (
idx < length - 1
? acc + cur
: (acc + cur) / length
), 0)a. 过滤非偶数
b. 折半
c. 累加
d. 计算平均值
2.2.举一些栗子🌰
Examples
例2:希望得到一个数组所有偶数值的一半的平均值
三、可以,这很函数式~
OK, It's Very Functional

3.1.函数是一等公民!
First Class Function
// 太傻了
const getServerStuff = function (callback) {
return ajaxCall(function (json) {
return callback(json)
})
}
// 这才像样
const getServerStuff = ajaxCall
// 下面来推导一下...
const getServerStuff
=== callback => ajaxCall(json => callback(json))
=== callback => ajaxCall(callback)
=== ajaxCall
// from JS函数式编程指南- 3.1.1.滥用匿名函数
3.1.函数是一等公民!
First Class Function
const BlogController = (function () {
const index = function (posts) {
return Views.index(posts)
}
const show = function (post) {
return Views.show(post)
}
const create = function (attrs) {
return Db.create(attrs)
}
const update = function (post, attrs) {
return Db.update(post, attrs)
}
const destroy = function (post) {
return Db.destroy(post)
}
return { index, show, create, update, destroy }
})()
// 以上代码 99% 都是多余的...const BlogController = {
index: Views.index,
show: Views.show,
create: Db.create,
update: Db.update,
destroy: Db.destroy,
}
// ...或者直接全部删掉
// 因为它的作用仅仅就是把视图(Views)
// 和数据库(Db)打包在一起而已。
// from JS函数式编程指南3.1.函数是一等公民!
First Class Function
// 原始函数
httpGet('/post/2', function (json) {
return renderPost(json)
})
// 假如需要多传递一个 err 参数
httpGet('/post/2', function (json, err) {
return renderPost(json, err)
})
// renderPost 将会在 httpGet 中调用,
// 想要多少参数,想怎么改都行
httpGet('/post/2', renderPost)- 3.1.2.为何钟爱一等公民?
要同时修改两处
啥都不用传
3.1.函数是一等公民!
First Class Function
// 只针对当前的博客
const validArticles = function (articles) {
return articles.filter(function (article) {
return article !== null && article !== undefined
})
}- 3.1.3.提高函数复用率
// 通用性好太多
const compact = function (xs) {
return xs.filter(function (x) {
return x !== null && x !== undefined
})
}3.1.函数是一等公民!
First Class Function
- 3.1.4.this
在函数式编程中,其实根本用不到 this...
但这里并不是说要避免使用 this
(江来报道上出了偏差...识得唔识得?)

3.2.柯里化
Curry
import { curry } from 'lodash'
const add = (x, y) => x + y
const curriedAdd = curry(add)
const increment = curriedAdd(1)
const addTen = curriedAdd(10)
increment(2) // 3
addTen(2) // 12- 3.2.1.柯里化概念
把接受多个参数的函数变换成一系列接受单一参数(从最初函数的第一个参数开始)的函数的技术。(注意是单一参数)
柯里化是由 Christopher Strachey 以逻辑学家 Haskell Curry 命名的
当然编程语言 Haskell 也是源自他的名字
虽然柯里化是由 Moses Schnfinkel 和 Gottlob Frege 发明的
3.2.柯里化
Curry
- 3.2.2.柯里化 VS 偏函数应用(partial application)
In computer science, partial application (or partial function application) refers to the process of fixing a number of arguments to a function, producing another function of smaller arity. -- by wikipedia
偏函数应用简单来说就是:一个函数,接受一个多参数的函数且传入部分参数后,返回一个需要更少参数的新函数。
import { curry, partial } from 'lodash'
const add = (x, y, z) => x + y + z
const curriedAdd = curry(add) // <- 只接受一个函数
const addThree = partial(add, 1, 2) // <- 不仅接受函数,还接受至少一个参数
=== curriedAdd(1)(2) // <- 柯里化每次都返回一个单参函数一个多参函数(n-ary),柯里化后就变成了 n * 1-ary,而偏函数应用了 x 个参数后就变成了 (n-x)-ary
3.2.柯里化
Curry
- 3.2.3.柯里化的实现
// 实现一个函数 curry 满足以下调用、
const f = (a, b, c, d) => { ... }
const curried = curry(f)
curried(a, b, c, d)
curried(a, b, c)(d)
curried(a)(b, c, d)
curried(a, b)(c, d)
curried(a)(b, c)(d)
curried(a)(b)(c, d)
curried(a, b)(c)(d)// ES5
var curry = function curry (fn, arr) {
arr = arr || []
return function () {
var args = [].slice.call(arguments)
var arg = arr.concat(args)
return arg.length >= fn.length
? fn.apply(null, arg)
: curry(fn, arg)
}
}
// ES6
const curry = (fn, arr = []) => (...args) => (
arg => arg.length >= fn.length
? fn(...arg)
: curry(fn, arg)
)([...arr, ...args])递归
3.2.柯里化
Curry
- 3.2.4.柯里化的意义
// 定义通用函数
const converter = (
toUnit,
factor,
offset = 0,
input
) => ([
((offset + input) * factor).toFixed(2),
toUnit,
].join(' '))
// 分别绑定不同参数
const milesToKm =
curry(converter)('km', 1.60936, undefined)
const poundsToKg =
curry(converter)('kg', 0.45460, undefined)
const farenheitToCelsius =
curry(converter)('degrees C', 0.5556, -32)
-- from https://stackoverflow.com/a/6861858代码复用
// 其实也可以不使用这些花里胡哨的柯里化啊,
// 偏函数应用啊什么的东东?
function converter (
ratio,
symbol,
input
) {
return (input * ratio).toFixed(2) +
' ' + symbol
}
converter(2.2, 'lbs', 4)
converter(1.62, 'km', 34)
converter(1.98, 'US pints', 2.4)
converter(1.75, 'imperial pints', 2.4)
-- from https://stackoverflow.com/a/32379766假如函数所需的参数无法同时得到?
3.3.函数组合
Function Composition
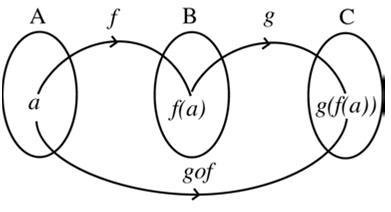
- 3.3.1.组合的概念
如果 y 是 w 的函数,w 又是 x 的函数,即 y = f(w), w = g(x),那么 y 关于 x 的函数 y = f[g(x)] 叫做函数 y = f(w) 和 w = g(x) 的复合函数。其中 w 是中间变量,x 是自变量,y 是函数值。
-- from 高中数学 复合函数
此外在离散数学里,应该还学过复合函数 f(g(h(x))) 可记为 (f ○ g ○ h)(x)。
-- 其实这就是函数组合
- 3.3.2.组合的实现
const add1 = x => x + 1
const mul3 = x => x * 3
const div2 = x => x / 2
// 结果是 3,但这样写可读性太差了
div2(mul3(add1(add1(0))))
const operate =
compose(div2, mul3, add1, add1)
operate(0) // => 相当于 div2(mul3(add1(add1(0))))
operate(2) // => 相当于 div2(mul3(add1(add1(2))))// redux 版
const compose = (...fns) => {
if (fns.length === 0) return arg => arg
if (fns.length === 1) return fns[0]
return fns.reduce((a, b) => (...args) => a(b(...args)))
}
// 一行版,支持多参数,但必须至少传一个函数
const compose = (...fns) => fns.reduceRight((acc, fn) => (...args) => fn(acc(...args)))
// 一行版,只支持单参数,但支持不传函数
const compose = (...fns) => arg => fns.reduceRight((acc, fn) => fn(acc), arg)3.3.函数组合
Function Composition

- 3.3.3.Pointfree
3.3.函数组合
Function Composition
Pointfree 即不使用所要处理的值,只合成运算过程。中文可以译作"无值"风格。 -- from Pointfree 编程风格指南
const addOne = x => x + 1
const square = x => x * x
const addOneThenSquare = compose(square, addOne)
addOneThenSquare(2) // 9// 非 Pointfree,因为提到了数据:word
const snakeCase = function (word) {
return word.toLowerCase().replace(/\s+/ig, '_')
}
// Pointfree
const snakeCase = compose(replace(/\s+/ig, '_'), toLowerCase)然而可惜的是,以上很 Pointfree 的代码会报错,
因为在 JS 中 replace 和 toLowerCase 函数是定义在 String 的原型链上的...
定义时,根本不需要提到要处理的值
- 3.3.3.Pointfree
3.3.函数组合
Function Composition
此外有的库(如 Underscore、Lodash...)把需要处理的数据放到了第一个参数。
const square = n => n * n;
_.map([4, 8], square) // 第一个参数是待处理数据
R.map(square, [4, 8]) // 一般函数式库都将数据放在最后1.无法柯里化后偏函数应用
2.无法进行函数组合
3.无法扩展 map(reduce 等方法) 到各种其他类型
-- 详情参阅参考文献之《Hey Underscore, You're Doing It Wrong!》
- 3.3.4.函数组合的意义
3.3.函数组合
Function Composition
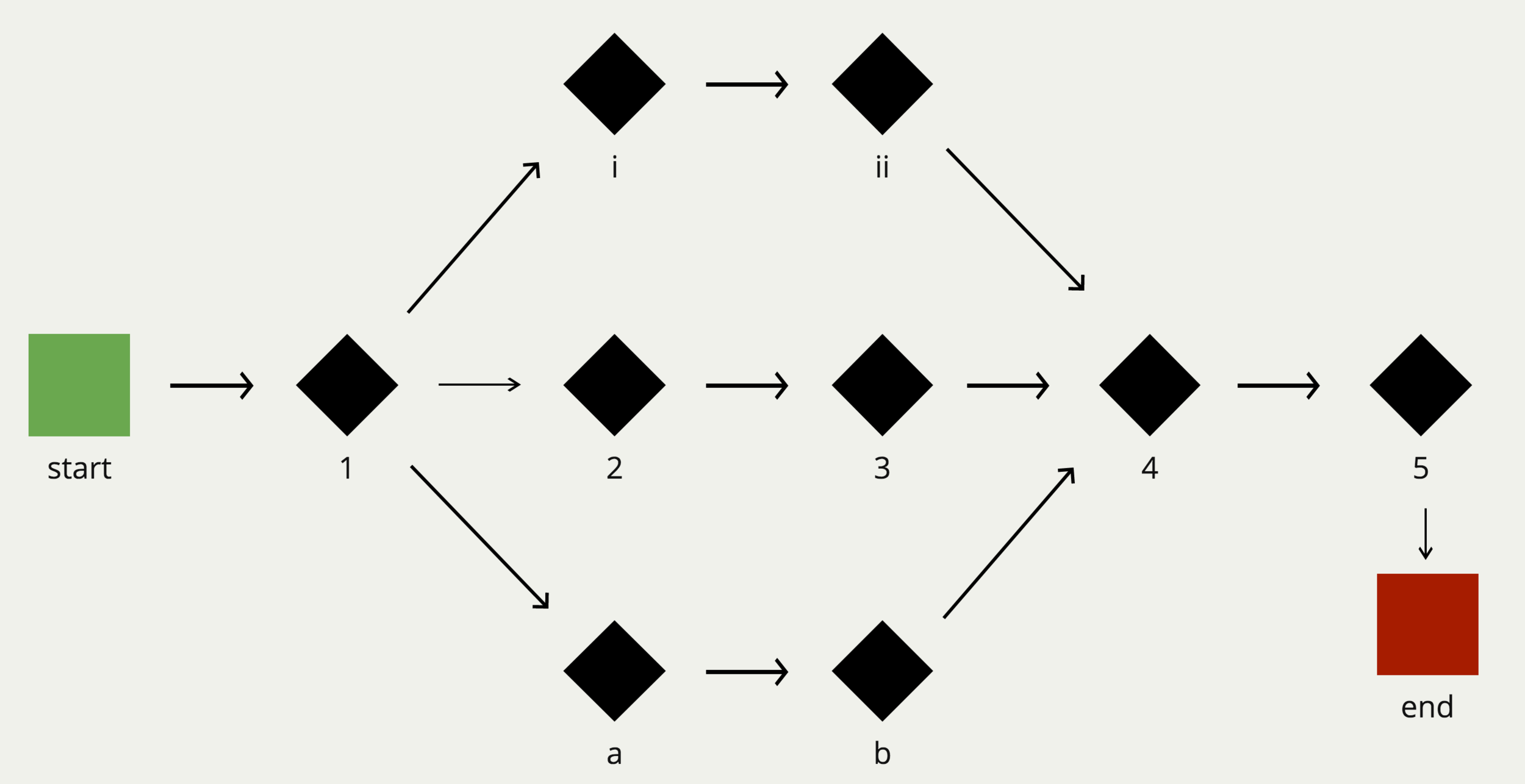
一个应用其实就是一个长时间运行的进程,并将一系列异步的事件转换为对应结果。

Start 可以是:
- 开启应用
- DOM 事件(DOMContentLoaded, onClick, onSubmit...)
- 接收到的 HTTP 请求
- 返回的 HTTP 响应
- 查询数据库的结果
- WebSocket 消息
- ..
End 可以是:
- 渲染或更新 UI
- 触发一个 DOM 事件
- 创建一个 HTTP 请求
- 返回一个 HTTP 响应
- 保存数据到 DB
- 发送 WebSocket 消息
- ...
- 3.3.4.函数组合的意义
3.3.函数组合
Function Composition
在 Start 和 End 之间的东东,我们可以看做数据流的变换(transformations)。
这些变换具体的说就是一系列的变换动词的结合。
这些动词描述了这些变换做了些什么(而不是怎么做)如:
- filter
- slice
- map
- reduce
- concat
- zip
- fork
- flatten
- ...
然而日常的数据流...



- 3.4.1.基本概念
3.4.Hindley-Milner 类型签名
Hindley-Milner Type Signatures
// id :: a -> a
const id = x => x
// map :: (a -> b) -> [a] -> [b]
const map = curry((f, xs) => xs.map(f))
// strLength :: String -> Number
const strLength = s => s.length
// join :: String -> [String] -> String
const join =
curry((what, xs) => xs.join(what))
// match :: Regex -> String -> [String]
const match =
curry((reg, s) => s.match(reg))
// replace :: Regex -> String -> String -> String
const replace = curry((reg, sub, s) => s.replace(reg, sub))在 Hindley-Milner 系统中,函数都写成类似 a -> b 这个样子,其中 a 和 b 是任意类型的变量。
多参函数为啥没有括号?
// 柯里化后可以不用一次传所有参数来调函数,
// 相当于首先传入 Regex 然后返回一个函数
// match :: Regex -> (String -> [String])
const match =
curry((reg, s) => s.match(reg))
// 可以看出柯里化后每传一个参数,
// 就会弹出类型签名最前面的那个类型。
// 以下就是传入 Regex 后返回的新函数
// onHoliday :: String -> [String]
const onHoliday = match(/holiday/ig)- 3.4.1.基本概念
3.4.Hindley-Milner 类型签名
Hindley-Milner Type Signatures
// id :: a -> a
const id = x => x
// head :: [a] -> a
const head = xs => xs[0]
// filter :: (a -> Bool) -> [a] -> [a]
const filter = curry((f, xs) => xs.filter(f))
// reduce :: (b -> a -> b) -> b -> [a] -> b
const reduce = curry((f, x, xs) => xs.reduce(f, x))a -> b 可以是从任意类型的 a 到任意类型的 b,但是 a -> a 必须是同一个类型。
例如,id 函数可以是 String -> String,也可以是 Number -> Number,但不能是 String -> Bool。
函数用括号包起来
同一类型变量
- 3.4.2.参数态(Parametricity)
3.4.Hindley-Milner 类型签名
Hindley-Milner Type Signatures
这个特性表明,函数将会以一种统一的行为作用于所有的类型。
// reverse :: [a] -> [a]以 reverse 函数为例,a 是任意类型,那么函数对每一个可能的类型的操作都必须保持统一。
仅从类型签名来看,reverse 可能的目的是什么?
- 它可以排序么?
我觉得不行,我觉得很普通~,没有足够的信息让它去为每一个可能的类型排序。 - 它能重新排列么?
我觉得还 ok,但它必须以一种可预料的方式达成目标。

Hoogle 是个针对 Haskell 的 api 搜索引擎,
厉害的地方是可以用类型签名来搜索...
- 3.4.3.自由定理(Free Theorems)
3.4.Hindley-Milner 类型签名
Hindley-Milner Type Signatures
// head :: [a] -> a
compose(f, head) === compose(head, map(f))
// filter :: (a -> Bool) -> [a] -> [a]
// 其中 p 是谓词函数
compose(map(f), filter(compose(p, f))) ===
compose(filter(p), map(f))
来自 Wadler 的论文
- 第一个例子意思是先取数组的第一个元素再对其应用函数 f,这操作与对整个数组都应用 f 再取第一个元素是等价的,但是前者要快得多。
- 第二个例子意思是先从数组中根据谓词函数 f、g 过滤出部分元素再对其应用函数 f,这操作与先对整个数组应用函数 f,再根据函数 g 过滤出相应元素是等价的,同样前者要快得多。
常识?但计算机没有常识...所以根据自由定理可以做一些计算优化~
- 3.4.4.类型约束
3.4.Hindley-Milner 类型签名
Hindley-Milner Type Signatures
签名也可以把类型约束为一个特定的接口(interface)
// sort :: Ord a => [a] -> [a]a 一定是个 Ord 对象,或者说 a 必须要实现 Ord 接口。
// assertEqual :: (Eq a, Show a) => a -> a -> Assertion两个类型约束:用于比较是否相等,并在不相等时打印差异
- 3.4.5.类型签名的作用
- 声明函数的输入和输出
- 让函数保持通用和抽象
- 可以用于编译时候检查
- 代码最好的文档
四、Talk is cheap!
Show me the ... MONEY!

4.1.容器
Box
const nextCharForNumStr = (str) =>
String.fromCharCode(parseInt(str.trim()) + 1)
nextCharForNumStr(' 64 ') // "A"- 1.怎么掐版
一层
二层
三层
四层
短短一行里居然
写了四层逻辑...

4.1.容器
Box
const nextCharForNumStr = (str) => {
const trimmed = str.trim()
const number = parseInt(trimmed)
const nextNumber = number + 1
return String.fromCharCode(nextNumber)
}
nextCharForNumStr(' 64 ') // 'A'- 2.改进版
这代码很不 pointfree...
const nextCharForNumStr = (str) => [str]
.map(s => s.trim())
.map(s => parseInt(s))
.map(i => i + 1)
.map(i => String.fromCharCode(i))
nextCharForNumStr(' 64 ') // ['A']- 3.借助数组版
包在数组里
4个map写逻辑


4.1.容器
Box
const Box = (x) => ({
map: f => Box(f(x)), // 返回容器为了链式调用
fold: f => f(x), // 将元素从容器中取出
inspect: () => `Box(${x})`, // 看容器里有啥
})
const nextCharForNumStr = (str) => Box(str)
...
.fold(c => c.toLowerCase()) // 可以轻易地继续调用新的函数
nextCharForNumStr(' 64 ') // 'a'- Box 定义
函数式编程一般约定,函子有一个 of 方法,用来生成新的容器。
Box(1) === Box.of(1)4.1.容器
Box
- 函子(Functor)
来自范畴学的概念
functor 是实现了 map 函数
并遵守一些特定规则的容器类型。
1. 规则一:
fx.map(f).map(g) === fx.map(x => g(f(x)))其实就是
函数组合
2. 规则二:
const id = x => x
fx.map(id) === id(fx)
4.2.Either
- 需求
获取对应颜色的十六进制的 RGB 值,并返回去掉`#`后的大写值。
const findColor = (name) => ({
red: '#ff4444',
blue: '#3b5998',
yellow: '#fff68f',
})[name]
const redColor = findColor('red')
.slice(1)
.toUpperCase() // FF4444
const greenColor = findColor('green')
.slice(1)
.toUpperCase()
// Uncaught TypeError:
// Cannot read property 'slice' of undefined
4.2.Either
- Either 定义和实现
// Either 由 Right 和 Left 组成
const Left = (x) => ({
map: f => Left(x), // 忽略传入的 f 函数
fold: (f, g) => f(x), // 使用左边的函数
inspect: () => `Left(${x})`, // 看容器里有啥
})
const Right = (x) => ({
map: f => Right(f(x)), // 返回容器为了链式调用
fold: (f, g) => g(x), // 使用右边的函数
inspect: () => `Right(${x})`, // 看容器里有啥
})either 类似于 box,主要的不同是 fold 函数要传递两个函数。
并且对于 left 来说 map 函数会忽略传入的函数。
4.2.Either
- 使用 either 的解法
const fromNullable = (x) => x == null
? Left(null)
: Right(x)
const findColor = (name) => fromNullable(({
red: '#ff4444',
blue: '#3b5998',
yellow: '#fff68f',
})[name])
findColor('green')
.map(c => c.slice(1))
.fold(
e => 'no color',
c => c.toUpperCase()
) // no colorLeft(null)
Left(null)
'no color'
4.3.Chain/FlatMap/bind/>>=
- 需求
// chain.js
const fs = require('fs')
const getPort = () => {
try {
const str = fs.readFileSync('config.json')
const { port } = JSON.parse(str)
return port
} catch(e) {
return 3000
}
}
const result = getPort() // 8888// config.json
{ "port": 8888 }读取 json 中的 port,出错就返回 3000
4.3.Chain/FlatMap/bind/>>=
- 使用 Either 重构一把
const tryCatch = (f) => {
try {
return Right(f())
} catch (e) {
return Left(e)
}
}
const getPort = () => tryCatch(
() => fs.readFileSync('config.json')
)
.map(c => JSON.parse(c))
.fold(e => 3000, c => c.port)这段代码有问题么?
parse 出错了咋办?
用 tryCatch 再包一层何如?
这里再包一层就变成:
- Right(Right(''))
- Right(Left(e))

4.3.Chain/FlatMap/bind/>>=
- 用 tryCatch + chain 再包一层
const Left = (x) => ({
...
chain: f => Left(x) // 和 map 一样,直接返回 Left
})
const Right = (x) => ({
...
chain: f => f(x), // 直接返回,不使用容器再包一层了
})
const getPort = () => tryCatch(
() => fs.readFileSync('config.json')
)
// 使用 chain 和 tryCatch
.chain(c => tryCatch(() => JSON.parse(c)))
.fold(e => 3000, c => c.port)4.3.Chain/FlatMap/bind/>>=
- 单子(Monad)
monad 是实现了 chain 函数并遵守一些特定规则的容器类型。
// 这里的 m 指的是一种 Monad 实例
const join = m => m.chain(x => x)1. 规则一:
join(m.map(join)) === join(join(m)2. 规则二:
// 这里的 M 指的是一种 Monad 类型
join(M.of(m) === join(m.map(M.of))
m.map(f) === m.chain(x => M.of(f(x)))说明了 map 可被 chain 和 of 所定义
monad 一定是 functor
4.4.半群
Semigroup
定义一:对于非空集合 S,若在 S 上定义了二元运算 ○,使得对于任意的 a, b ∈ S,有 a ○ b ∈ S,则称 {S, ○} 为广群。
定义二:若 {S, ○} 为广群,且运算 ○ 还满足结合律,即:任意 a, b, c ∈ S,有 (a ○ b) ○ c = a ○ (b ○ c),则称 {S, ○} 为半群。
// 字符串和 concat 是半群
'1'.concat('2').concat('3') === '1'.concat('2'.concat('3'))
// 数组和 concat 是半群
[1].concat([2]).concat([3]) === [1].concat([2].concat([3]))例如 JavaScript 中有 concat 方法的对象都是半群。
- 半群的定义
4.4.半群
Semigroup
const Sum = (x) => ({
x,
concat: ({ x: y }) => Sum(x + y), // 采用解构获取值
inspect: () => `Sum(${x})`,
})
Sum(1).concat(Sum(2)).inspect() // Sum(3)那么对于 <Number, +> 来说它符合半群的定义吗?
- 数字相加返回的仍然是数字(广群)
- 加法满足结合律(半群)
但是数字并没有 concat 方法...
- Sum
4.4.半群
Semigroup
const All = (x) => ({
x,
concat: ({ x: y }) => All(x && y), // 采用解构获取值
inspect: () => `All(${x})`,
})
All(true).concat(All(false)).inspect() // All(false)同理, <Boolean, &&> 也满足半群的定义
- All 与 First
const First = (x) => ({
x,
concat: () => First(x), // 忽略后续的值
inspect: () => `First(${x})`,
})
First('blah').concat(First('yo')).inspect() // First('blah')对于字符串创建一个新的半群 <String, First>(只返回第一个参数)
4.4.半群
Semigroup
const data1 = {
name: 'steve',
isPaid: true,
points: 10,
friends: ['jame'],
}假设有以下两个数据,需要将其合并
- 半群的应用
First
All
Sum
Array
const concatObj = (obj1, obj2) => Object.entries(obj1)
.map(([ key, val ]) => ({
// concat 两个对象的值
[key]: val.concat(obj2[key]),
}))
.reduce((acc, cur) => ({ ...acc, ...cur }), {})
concatObj(data1, data2)const data2 = {
name: 'steve',
isPaid: false,
points: 2,
friends: ['young'],
}4.5.幺半群
Monoid
- 幺半群的定义
幺半群是一个存在单位元(幺元)的半群。
单位元:对于半群 <S, ○>,存在 e ∈ S,
使得任意 a ∈ S 有 a ○ e = e ○ a
- 对于 <Number, +> 来说单位元就是 0
- 对于 <Number, *> 来说单位元就是 1
- 对于 <Boolean, &&> 来说单位元就是 true
- 对于 <Boolean, ||> 来说单位元就是 false
- 对于 <Number, Min> 来说单位元就是 Infinity
- 对于 <Number, Max> 来说单位元就是 -Infinity
那么 <String, First> 是幺半群么?
4.5.幺半群
Monoid
- <String, First> 不是幺半群
// 我们找不到这样的单位元 e 满足以下等式
First(e).concat(First('str')) ===
First('str').concat(First(e))- 安全的幺半群
const sum = xs => xs.reduce((acc, cur) => acc + cur, 0)
const all = xs => xs.reduce((acc, cur) => acc && cur, true)
// first 没有单位元
const first = xs => xs.reduce(acc, cur) => acc)
sum([]) // 0,而不是报错!
all([]) // true,而不是报错!
first([]) // boom!!!4.6.foldMap
- 1.套路
const Monoid = (x) => ({ ... })
const monoid = xs => xs.reduce(
(acc, cur) => acc.concat(cur), // 使用 concat 结合
Monoid.empty() // 传入幺元
)
monoid([Monoid(a), Monoid(b), Monoid(c)]) // 传入幺半群实例- 2.List、Map —— from immutable
顾名思义,正好对应原生的 Array 和 Object
然而库中并没有定义 empty 属性和 fold 方法
4.6.foldMap
- 3.利用 List、Map 重构
import { List, Map } from 'immutable'
const derived = {
fold (empty) {
return this.reduce(
(acc, cur) => acc.concat(cur),
empty
)
},
}
List.prototype.empty = List()
List.prototype.fold = derived.fold
Map.prototype.empty = Map({})
Map.prototype.fold = derived.fold
// from https://github.com/DrBoolean/immutable-ext4.6.foldMap
- 3.利用 List、Map 重构
List.of(1, 2, 3)
.map(Sum)
.fold(Sum.empty()) // Sum(6)
List().fold(Sum.empty()) // Sum(0)
Map({ steve: 1, young: 3 })
.map(Sum)
.fold(Sum.empty()) // Sum(4)
Map().fold(Sum.empty()) // Sum(0)注意到 map 和 fold 这两步操作,从逻辑上来说是一个操作,所以我们可以新增 foldMap 方法来结合两者。
4.6.foldMap
- 4.利用 foldMap 重构
const derived = {
fold (empty) { ... },
foldMap (f, empty) {
return empty != null
// 幺半群中将 f 的调用放在 reduce 中,提高效率
? this.reduce(
(acc, cur, idx) => acc.concat(f(cur, idx)),
empty
)
: this.map(f) // 在 map 中调用 f 是因为考虑到空的情况
.reduce((acc, cur) => acc.concat(cur))
},
}
List.of(1, 2, 3).foldMap(Sum, Sum.empty()) // Sum(6)
List().foldMap(Sum, Sum.empty()) // Sum(0)
Map({ a: 1, b: 3 }).foldMap(Sum, Sum.empty()) // Sum(4)
Map().foldMap(Sum, Sum.empty()) // Sum(0)4.7.拖延症容器
虽然你可以不停地用 map 给它分配任务,
但是只要你不调用 fold 方法催它执行,它就死活不执行...
const LazyBox = (g) => ({
map: f => LazyBox(() => f(g())),
fold: f => f(g()),
})
const result = LazyBox(() => ' 64 ')
.map(s => s.trim())
.map(i => parseInt(i))
.map(i => i + 1)
.map(i => String.fromCharCode(i))
// 没有 fold 死活不执行
result.fold(c => c.toLowerCase()) // aLazyBox
4.8.任务
Task
- 1.基本介绍
import Task from 'data.task'
const showErr = e => console.log(`err: ${e}`)
const showSuc = x => console.log(`suc: ${x}`)
Task.of(1).fork(showErr, showSuc) // suc: 1
Task.of(1).map(x => x + 1)
.fork(showErr, showSuc) // suc: 2
// 类似 Left
Task.rejected(1).map(x => x + 1)
.fork(showErr, showSuc) // err: 1
Task.of(1).chain(x => new Task.of(x + 1))
.fork(showErr, showSuc) // suc: 24.8.任务
Task
- 2.使用示例
const lauchMissiles = () => (
// 和 promise 很像,不过 promise 会立即执行
// 而且参数的位置也相反
new Task((rej, res) => {
console.log('lauchMissiles')
res('missile')
})
)
// 继续对之前的任务添加后续操作(duang~给飞弹加特技!)
const app = lauchMissiles()
.map(x => x + '!')
// 这时才执行(发射飞弹)
app.fork(showErr, showSuc)4.8.任务
Task
- 3.原理意义
我们将有副作用的代码给包起来之后,
这些新函数就都变成了纯函数,
这样我们的整个应用的代码都是纯的~,
并且在代码真正执行前(fork 前)
还可以不断地 compose 别的函数增加逻辑。

4.8.任务
Task
- 4.异步嵌套示例
- 读取 config1.json 中的数据
- 将内容中的 8 替换成 6
- 将新内容写到 config2.json 中
import fs from 'fs'
const app = () => (
fs.readFile('config1.json', 'utf-8', (err, contents) => {
if (err) throw err
const newContents = content.replace(/8/g, '6')
fs.writeFile('config2.json', newContents, (err, _) => {
if (err) throw err
console.log('success!')
})
})
)4.8.任务
Task
- 4.异步嵌套示例
- 读取 config1.json 中的数据
- 将内容中的 8 替换成 6
- 将新内容写到 config2.json 中
import fs from 'fs'
import Task from 'data.task'
const cfg1 = 'config1.json'
const cfg2 = 'config2.json'
const readFile = (file, enc) => (
new Task((rej, res) =>
fs.readFile(file, enc, (err, str) =>
err ? rej(err) : res(str)
)
)
)
const writeFile = (file, str) => (
new Task((rej, res) =>
fs.writeFile(file, str, (err, suc) =>
err ? rej(err) : res(suc)
)
)
)const app = readFile(cfg1, 'utf-8')
.map(
str => str.replace(/8/g, '6')
)
.chain(
str => writeFile(cfg2, str)
)
app.fork(
e => console.log(`err: ${e}`),
x => console.log(`suc: ${x}`)
)4.9.Applicative Functor
- 1.问题引入
Applicative Functor 提供了让
不同的函子(functor)互相应用的能力。
const add = x => y => x + y
add(Box.of(2))(Box.of(3)) // NaN
Box(2).map(add).inspect() // Box(y => 2 + y)为啥我们需要函子的互相应用?什么是互相应用?
现在我们有了一个容器,它的内部值为
局部调用(partially applied)后的函数。
接着想让它应用到 Box(3) 上,最后得到 Box(5) 的预期结果。
4.9.Applicative Functor
- 1.问题引入 —— chain
Box(2)
.chain(x => Box(3).map(add(x)))
.inspect() // Box(5)成功实现~,BUT,这种实现方法有个问题,
那就是单子(Monad)的执行顺序问题。
首先执行
等待 Box(2) 执行完毕
必须等 Box(2) 执行完毕后,
才能对 Box(3) 进行求值。
假如这是两个异步任务,
那么完全无法同时并行执行。
4.9.Applicative Functor
- 2.基本介绍
const Box = (x) => ({
// 这里 box 是另一个 Box 的实例,x 是函数
ap: box => box.map(x),
...
})
Box(add)
// Box(y => 2 + y) ,咦?在哪儿见过?
.ap(Box(2))
.ap(Box(3)) // Box(5)F(x).map(f) === F(f).ap(F(x))
// 这就是为什么
Box(2).map(add) === Box(add).ap(Box(2))运算规则
4.9.Applicative Functor
- 3.Lift 家族
// F 该从哪儿来?
const fakeLiftA2 = f => fx => fy => F(f).ap(fx).ap(fy)
// 应用运算规则转换一下~
const liftA2 = f => fx => fy => fx.map(f).ap(fy)
liftA2(add, Box(2), Box(4)) // Box(6)
// 同理
const liftA3 = f => fx => fy => fz =>
fx.map(f).ap(fy).ap(fz)
const liftA4 = ...
...
const liftAN = ...4.9.Applicative Functor
- 4.Lift 应用
// 假装是个 jQuery 接口~
const $ = selector =>
Either.of({ selector, height: 10 })
const getScreenSize = screen => head => foot =>
screen - (head.height + foot.height)
// Right(780)
liftA2(getScreenSize(800))($('header'))($('footer'))// List 的笛卡尔乘积
List.of(x => y => z => [x, y, z].join('-'))
.ap(List.of('tshirt', 'sweater'))
.ap(List.of('white', 'black'))
.ap(List.of('small', 'medium', 'large'))4.9.Applicative Functor
- 4.Lift 应用
const Db = ({
find: (id, cb) =>
new Task((rej, res) =>
setTimeout(() => res({ id, title: `${id}`}), 100)
)
})
const reportHeader = (p1, p2) =>
`Report: ${p1.title} compared to ${p2.title}`
Task.of(p1 => p2 => reportHeader(p1, p2))
.ap(Db.find(20))
.ap(Db.find(8))
// Report: 20 compared to 8
.fork(console.error, console.log)
liftA2
(p1 => p2 => reportHeader(p1, p2))
(Db.find(20))
(Db.find(8))
// Report: 20 compared to 8
.fork(console.error, console.log)4.10.Traversable
import fs from 'fs'
// 详见 4.8.
const readFile = (file, enc) => (
new Task((rej, res) => ...)
)
const files = ['a.js', 'b.js']
// [Task, Task],我们得到了一个 Task 的数组
files.map(file => readFile(file, 'utf-8'))然而我们想得到的是一个包含数组的 Task([file1, file2]),
这样就可以调用它的 fork 方法,查看执行结果。
- 1.问题引入
files
.traverse(Task.of, file => readFile(file, 'utf-8'))
.fork(console.error, console.log)4.10.Traversable
Array.prototype.empty = []
// traversable
Array.prototype.traverse = function (point, fn) {
return this.reduce(
(acc, cur) => acc
.map(z => y => z.concat(y))
.ap(fn(cur)),
point(this.empty)
)
}- 2.实现
单位元
acc: 累加器
看到代码先别晕~,让咱们来分析下:
- reduce: 从左到右遍历元素
- z => y => z.concat(y): 函子间的调用函数,合并半群
- fn(cur): 被调用的函子
所以相当于遍历一遍数组,将每个元素用 fn 调用后合并返回
cur: 当前值
合并半群
4.11.自然变换
Natural Transformation
- 1.基本概念
自然变换就是一个函数,接受一个函子(functor),返回另一个函子。
const boxToEither = b => b.fold(Right)Box
Either
自然变换
Left?
nt(x).map(f) == nt(x.map(f))满足规则:

const res1 = boxToEither(Box(100))
.map(x => x * 2)
const res2 = boxToEither(
Box(100).map(x => x * 2)
)
res1 === res2 // Right(200)4.11.自然变换
Natural Transformation
- 2.应用场景
const arr = [2, 400, 5, 1000]
const first = xs => fromNullable(xs[0])
const double = x => x * 2
const getLargeNums = xs => xs.filter(x => x > 100)
first(
getLargeNums(arr)
.map(double)
)
// 根据自然变换,它显然和下面的式子是等价的
// 但是下式的性能显然好得多
first(getLargeNums(arr))
.map(double)例1:得到一个数组小于等于 100 的最后一个数的两倍的值
4.11.自然变换
Natural Transformation
- 2.应用场景
例2:找到 id 为 3 的用户的最好的朋友的 id
// Task(Either(user))
const zero = Db.find(3)
// 第一版
// Task(Either(Task(Either(user)))) ???
const one = zero
.map(either => either
.map(user => Db
.find(user.bestFriendId)
)
)
.fork(
console.error,
either => either // Either(Task(Either(user)))
.map(t => t.fork( // Task(Either(user))
console.error,
either => either
.map(console.log), // Either(user)
))
)
// 假 api
const fakeApi = (id) => ({
id,
name: 'user1',
bestFriendId: id + 1,
})
// 假 Db
const Db = {
find: (id) => new Task(
(rej, res) => (
res(id > 2
? Right(fakeApi(id))
: Left('not found')
)
)
)
}4.11.自然变换
Natural Transformation
- 2.应用场景
例2:找到 id 为 3 的用户的最好的朋友的 id
// Task(Either(user))
const zero = Db.find(3)
// 第二版
const two = zero
.chain(either => either
.fold(Task.rejected, Task.of) // Task(user)
.chain(user => Db
.find(user.bestFriendId) // Task(Either(user))
)
.chain(either => either
.fold(Task.rejected, Task.of) // Task(user)
)
)
.fork(
console.error,
console.log,
)多余嵌套
// 假 api
const fakeApi = (id) => ({
id,
name: 'user1',
bestFriendId: id + 1,
})
// 假 Db
const Db = {
find: (id) => new Task(
(rej, res) => (
res(id > 2
? Right(fakeApi(id))
: Left('not found')
)
)
)
}4.11.自然变换
Natural Transformation
- 2.应用场景
// 假 api
const fakeApi = (id) => ({
id,
name: 'user1',
bestFriendId: id + 1,
})
// 假 Db
const Db = {
find: (id) => new Task(
(rej, res) => (
res(id > 2
? Right(fakeApi(id))
: Left('not found')
)
)
)
}例2:找到 id 为 3 的用户的最好的朋友的 id
// Task(Either(user))
const zero = Db.find(3)
// 第三版
const three = zero
.chain(either => either
.fold(Task.rejected, Task.of) // Task(user)
)
.chain(user => Db
.find(user.bestFriendId) // Task(Either(user))
)
.chain(either => either
.fold(Task.rejected, Task.of) // Task(user)
)
.fork(
console.error,
console.log,
)重复逻辑
4.11.自然变换
Natural Transformation
- 2.应用场景
例2:找到 id 为 3 的用户的最好的朋友的 id
// 将 Either 变换成 Task
const eitherToTask = (e) => (
e.fold(Task.rejected, Task.of)
)
// 第四版
const four = zero
.chain(eitherToTask) // Task(user)
.chain(user => Db
// Task(Either(user))
.find(user.bestFriendId)
)
.chain(eitherToTask) // Task(user)
.fork(
console.error,
console.log,
)自然变换
// 出错版
const error = Db.find(2)
// Task.rejected('not found')
.chain(eitherToTask)
// 这里永远不会被调用,被跳过了
.chain(() => console.log('hey man'))
...
.fork(
console.error, // not found
console.log,
)4.12.同构
Isomorphism
- 1.定义
同构是在数学对象之间定义的一类映射,它能揭示出在这些对象的属性或者操作之间存在的关系。
简单来说就是两种不同类型的对象经过变形,保持结构并且不丢失数据。
to(from(x)) === x
from(to(y)) === y一对儿函数
from/to
无损地保存同样的信息
4.12.同构
Isomorphism
- 2.应用场景
例1:[Char] 和 String 同构
// String ~ [Char]
const Iso = (to, from) => ({ to, from })
const chars = Iso(
s => s.split(''),
c => c.join('')
)
const str = 'hello world'
chars.from(chars.to(str)) === str这能有啥用呢?
const truncate = (str) => (
chars.from(
// 我们先用 to 方法将其转成数组
// 这样就能使用数组的各类方法
chars.to(str).slice(0, 3)
).concat('...')
)
truncate(str) // hel...4.12.同构
- 2.应用场景
例2:再来看看最多有一个参数的数组 [a] 和 Either 的同构关系
// [a] ~ Either null a
const singleton = Iso(
e => e.fold(() => [], x => [x]),
([ x ]) => x ? Right(x) : Left()
)
const filterEither = (e, pred) => singleton
.from(
singleton
.to(e)
.filter(pred)
)const getUCH = str => filterEither(
Right(str),
x => x.match(/h/ig)
).map(x => x.toUpperCase())
getUCH('hello') // Right(HELLO)
getUCH('ello') // Left(undefined)Isomorphism
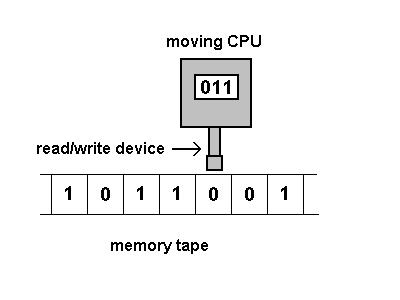
λ演算 VS 图灵机
Alonzo Church VS Alan Turing


参考文献
functional-programming-in-javascript
By steve young
functional-programming-in-javascript
JavaScript函数式编程
- 8,078