圖論2
最短路徑、最小生成樹
接下來\(V\) 代表點數、\(E\) 代表邊數
\((u,v)\)代表由\(u\)通往\(v\)的邊
單點源最短路徑
鬆弛(Relaxation)
假設除了起點,到別的點的距離都是 \(\infty\)
若邊\((u,v)\)之權重為\(w\)
則更新\(dis[v] =min(dis[v],dis[u] + w)\)
Bellman-Ford演算法
可以發現,我們每次做鬆弛,其實就是模擬走一條邊,所以我們只要好好模擬這個過程就可以了。
複雜度: \(O(VE)\)
DP想法!!
優化:
會發現其實並不需要鬆弛那麼多次,只要在知道\(dis[u]\)是最小的情況下,直接拿這個點對其他點做鬆弛就好了。
怎麼知道\(dis[u]\)最小了呢?
經過鬆弛後的結果一定比\(dis[u]\)大(無負邊情況下)
故只要\(u\)是所有未知的點中距離最小的,\(dis[u]\)一定已是最小的,固可拿來幫其他的做鬆弛。
Dijkstra's Algorithm
用pq維護還沒鬆弛過的點
取距離最小者來鬆其他點直到全部都被鬆過為止
複雜度:\(O((V+E)logE)\)
int dis[MAXN];
vector<pair<int,int>> graph[MAXN];
void dijkstra_algorithm(int start,int end){
priority_queue<pair<int,int>,vector<pair<int,int>>,greater<pair<int,int>>> pq;
bool visited[n+1] = {false};
for(int i=1;i<=n;i++) dis[i] = INF;
dis[start] = 0;
pq.push({0,start});
while(pq.size()){
auto [w,v] = pq.top();
pq.pop();
if(visited[v]) continue;
visited[v] = 1;
for(auto [w_2,v_2]:graph[v]){
if(w+w_2<dis[v_2]){//relaxation
dis[v_2] = w+w_2;
pq.push({dis[v_2],v_2});
}
}
}
}dijkstra不能處理負邊!
題目:
次短路徑
多點源最短路徑
Floyd-Warshall Algorithm
bj4 跟Bellman-Ford證明很像
可以自己找(我懶)
int dis[MAXN][MAXN];
void Floyd_Warshall(int start,int end){
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
for(int k=1;k<=n;k++){
dis[i][j] = min(dis[i][j],dis[i][k]+dis[k][j]);
}
}
}
}\(dis[i][j]\)要先預處理好!
複雜度:\(O(n^3)\)
題目:
MST
最小生成樹
生成樹?
定義:
對於一張圖,只取裡面的幾條邊,組成一棵樹,並讓邊權之和最小。
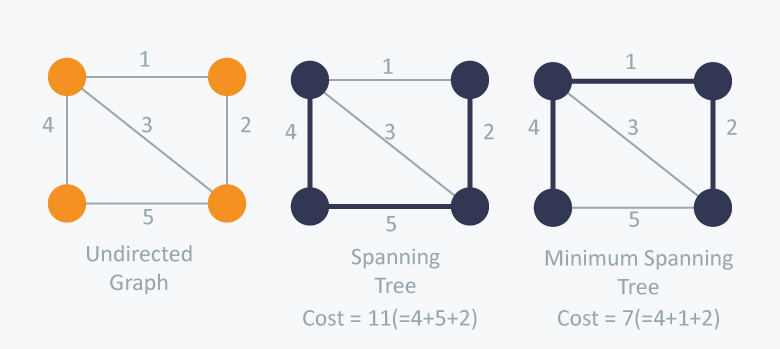
明顯的觀念:
1.只要連了\(V-1\)條邊後MST就做好了(樹的性質)
2.要讓邊權和最小,取邊權最小的邊比較好(廢話)
Prim's algorithm
跟前面dijkstra's有87%相似
隨便選一個起點,每次向外找邊權最小的邊加進MST,再繼續上述步驟直到\(V-1\)條邊為止。
複雜度:\(O((V+E)logE)\)
Other solutions?
10
5
兩條紅線 你要選哪個來連接兩個MST?
Kruskal's Algorithm
做法:
照邊權排序
取邊權最小的邊
若兩個點屬於不同MST,就透過該邊合併
重複直到\(V-1\)條邊
第三步怎麼做到?
並查集
Disjoin-Set Union(DSU)
合併Union:將兩個集合合併
查詢Query:查詢一個點處在的集合
TODO:
聽不懂? 用幫派來解釋!
合併Union:將兩個幫派合併成一個
查詢Query:檢查這個人是哪個幫派的
合併Union:把其中一個人的首領變另個的手下
查詢Query:看兩個人幫派的首領一不一樣
路徑壓縮:最後都是只查首領,所以改成直接紀錄首領是誰,遞迴時沿路更改。\(O(N)->O(1)\)
const int MAXN = (int)2e5;
int dsu[MAXN]; //第i項表示i點的父節點
void Init(){
for (int i=0;i<MAXN;i++) dsu[i] = i;
}
//先將每項的父元素設為本身
int query(int k){
if (k==dsu[k]) return k;
dsu[k] = query(dsu[k]);//老大的老大就是我的老大
return dsu[k];
}
void modify (int x,int y){
int xA = query(x);
int yA = query(y);
if (xA!=yA) dsu[xA] = yA;
}簡單的DSU題目練習:CF445B
Back to Kruskal!
\(O(ElogE)\)
先試著利用kruskal的概念自己寫寫看演算法吧!
struct road{
ll f;
ll s;
ll val;
};
int dsu[MAXN];
vector<road> graph;
int find(int x){
return dsu[x] == x ? x : dsu[x] = find(dsu[x]);
}
void modify(int x,int y){
int pa = find(x);
int pb = find(y);
if(pa!=pb) dsu[pb] = pa;
}
void solve(){
int n,m;
cin>>n>>m;
for(int i=1;i<=n;i++) dsu[i] = i;
while(m--){
road r;
cin>>r.f>>r.s>>r.val;
graph.pb(r);
}
ll sum = 0;
sort(all(graph),[](road a,road b){return a.val<b.val;});
for(auto [a,b,c]:graph){
if(find(a)!=find(b)){
sum+=c;
modify(a,b);
}
}
cout<<sum<<endl;
return;
}
題目:
提示:
邊權為0,1的圖,如果能做出權重\(a,b(a<b)\)的生成樹,則可以做出\([a,b]\)權重的生成樹。
圖論2
By yeedrag
圖論2
- 744



