線段樹

建國中學 游承曦

什麼是資結阿阿阿!????

如果你不知道是什麼

你可以參考這裡：

https://slides.com/youou/stl_data_structure

(x)

資料結構是拿來儲存資料的 (廢話)

它又分成具體的和抽象的

具體的有像是

Stack (堆疊)、Queue (佇列)

抽象的有像是

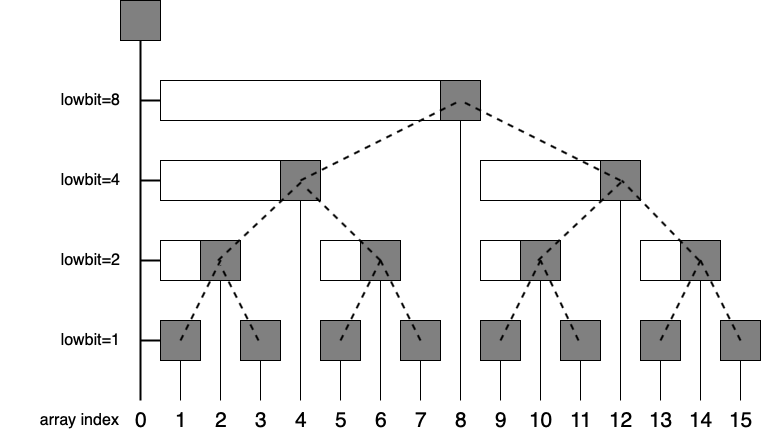
線段樹、BIT (Binary Indexed Tree)

今天的先備知識

  1.  函式 / 遞迴

  2. 分治法 D&Q

  3. 樹與二元樹概念

  4. 仙貝

都忘記了?

函式

架構

回傳型別 函式名稱(參數型別1 參數名稱1, ...){
//  do something
    回傳參數;
}

栗子

void uhhh(int a, int b){
    a = a + b;
}
int main(){
    int x, y;
    cin >> x >> y;
    uhhh(x, y);
    cout << x << " " << y << endl;
}

遞迴：狒是數列

int f(int n){
    if(n == 1 || n == 2){
        return 1;
    }
    else{
        return f(n-1) + f(n-2);
    }
}

aka 自己呼叫自己

分治

Divide & Conquer

把問題切成好幾塊

1. 切成子問題

2. 解決子問題

3. 合併子問題

Main Idea

栗子1. Merge Sort

Step3. 合併兩個已經有序的數列成一個

Step1. 把序列切成兩半

Step2. 遞迴排序各自兩半

void MergeSort(int l, int r){
    if(l >= r) return;
    
    // Divide
    int m = (l + r) / 2;
    MergeSort(l, m), MergeSort(m+1, r);
    
    // Conquer
    int i = l, j = m+1, k = l;
    while(i <= m && j <= r){
        if(arr[i] < arr[j]) buf[k++] = arr[i++];
        else buf[k++] = arr[j++];
    }
    while(i <= m) buf[k++] = arr[i++];
    while(j <= r) buf[k++] = arr[j++];
    for(int p=l ; p<=r ; ++p) arr[p] = buf[p];
}

栗子2. 逆序數對

給一個數列 \(a\)，

求有多少對 \((i, \ j)\) 符合 \(i < j\) 且 \(a_i > a_j\) ?

在做 Merge Sort 合併時

順便計算橫跨兩邊的組合數!

int MergeSort(int l, int r){
    if(l >= r) return 0;
    
    // Divide
    int m = (l + r) / 2;
    int cnt = MergeSort(l, m) + MergeSort(m+1, r);
    
    // Conquer
    int i = l, j = m+1, k = l;
    while(i <= m && j <= r){
        if(arr[i] <= arr[j]) buf[k++] = arr[i++];
        else{
            cnt += m - i + 1;
            buf[k++] = arr[j++];
        }
    }
    while(i <= m) buf[k++] = arr[i++];
    while(j <= r) buf[k++] = arr[j++];
    for(int p=l ; p<=r ; ++p) arr[p] = buf[p];
    return cnt;
}

樹

Tree

現實生活中的樹

資訊領域中的樹

實際上，他長這樣

A

B

C

F

G

H

E

D

根節點

葉節點

父節點

子節點

二元樹

A

B

C

E

D

F

G

1. 每個節點都只有\(\leq 2\)個子節點

2. 第\(k\)層最多有\(2^k\)個節點

3. 深度為\(k\)的二元樹最多有

\(2^{k+1}-1\)個節點

H

I

如果把節點編號?

1

2

3

5

4

6

7

9

12

從根節點為\(1\)開始 (1-base)

對於一個節點編號 \(k\)，

則左子節點編號 \(2k\)，

右子節點編號 \(2k+1\)

於是就可以用一條陣列存一棵二元樹了!

Range

Maximum/Minimum

Query

(RMQ)

給一個序列 \(a\)，

多次詢問某個區間 \([L, R]\) 裡的最大or最小值

\(N \leq 10^5\)，\(Q \leq 10^5\)

直接的想法

int mx = -2147483648;
for(int i=L ; i<=R ; i++) mx = max(mx, a[i]);
cout << mx << endl;

然後你就發現你 TLE (Time Limit Exceed) 了

仔細想想，如果查區間 \([1,10^5] \times 10^5\) 次

那需要 \(10^{10}\) 次運算欸

複雜度 \(\mathcal{O}(n^2)\) 超爛的

於是線段樹

出現了 (x)

線段樹

Segment Tree

如果我們可以維護一個區間的答案?

6

6

4

5

6

3

4

\([1, 6]\)

\([1, 3]\)

\([4, 6]\)

\([1,2]\)

\([3]\)

\([4, 5]\)

\([6]\)

6

1

\([1]\)

\([2]\)

3

2

\([4]\)

\([5]\)

\(a:\{1,6,5,2,3,4\}\)

如果查詢區間 \([2, 5]\) 最大值

6

6

4

5

6

3

4

\([1, 6]\)

\([1, 3]\)

\([4, 6]\)

\([1,2]\)

\([3]\)

\([4, 5]\)

\([6]\)

6

1

\([1]\)

\([2]\)

3

2

\([4]\)

\([5]\)

6

6

4

3

3

6

5

6

每個節點存一個區間內的資料!

  • 線段樹是一棵二元樹，每個節點維護一個區間的值

  • 兩個子節點維護的是把原本的區間切一半的左右兩邊

  • 因為是二元樹，如果原序列有 \(N\) 項，則深度最大為 \(\log N\) 層

  • 所以每次查詢的複雜度最差為 \(\mathcal{O}(\log N)\)

食祚方式

  • 指標型

  • 陣列型

  • 偽指標型 (重載 "->" 運算子)

二元樹

Wiwihorz

指標型

struct Node{
    Node *l, *r;
    int max_val;
    Node(int v):l(NULL), r(NULL), max_val(v){}
} *rt;

你會需要這些東西:D

但顯然我沒有要講它:DDD

陣列型

還記得剛剛才說二元樹可以用一條陣列存嗎?

線段樹也可以!

因為編號的關係，

線段樹的陣列大小要開到原序列的\(4\)倍大

cur

cur*2

cur*2 + 1

#include <iostream>
using namespace std;
#define N 100005

int arr[N];
int sgt[N * 4];
int main(){

}

建樹：遞迴把原序列塞到線段樹裡

void build(int l, int r, int o){
    if(l == r){
         sgt[o] = arr[l];
         return;
    }
    
    int m = (l + r) / 2;
    build(l, m, o * 2);
    build(m+1, r, o * 2 + 1);
    
    sgt[o] = max(sgt[o*2], sgt[o*2+1]);
}

原序列\(N\)項構造出的線段樹會有\(2N-1\)個節點

因此建樹的複雜度就是 \(\mathcal{O}(N)\) !

然後我們就可以做RMQ了!

區間查詢的部分

假設現在查到的區間為 \([ql, qr]\)

可能會有下面四種情況：

  1. 查詢的區間完整包覆節點的區間 \(ql \leq L \ and \ R \leq qr\)

  2. 查詢的右界在節點區間中間以左 \(qr \leq M\)

  3. 查詢的左界在節點區間中間以右 \(ql > M\)

  4. 查詢的區間橫跨左右子節點 \(L \leq ql \leq M < qr \leq R\)

若節點區間為 \([L, R]\)，則區間中點為 \(M\)

\(L\)

\(M\)

\(R\)

\(ql\)

\(qr\)

1. 查詢的區間橫跨節點區間

直接回傳節點的資訊!

\(L\)

\(M\)

\(R\)

\(ql\)

\(qr\)

2. 查詢的右界在區間中點以左

\(L\)

\(M\)

\(ql\)

\(qr\)

2. 查詢的右界在區間中點以左

往左子節點遞迴找答案!

3. 查詢的左界在區間中點以右

同理往右子節點遞迴找答案!

\(L\)

\(M\)

\(R\)

\(ql\)

\(qr\)

4. 橫跨左右子節點

\(L\)

\(M\)

\(R\)

\(ql\)

\(qr\)

4. 橫跨左右子節點

\(L\)

\(M\)

\(R\)

\(ql\)

\(M\)

\(qr\)

拆成兩邊找答案再合併 Oao

4. 橫跨左右子節點

拆成兩邊找答案再合併 Oao

\(L\)

\(M\)

\(R\)

\(ql\)

\(qr\)

int Query(int ql, int qr, int L, int R, int o){
    if(ql <= L && R <= qr){
        return sgt[o];
    }
    int m = (L + R) / 2;
    if(qr <= m){
        return Query(ql, qr, L, m, o * 2);
    }
    else if(ql >= m + 1){
        return Query(ql, qr, m+1, R, o * 2 + 1);
    }
    else{
        return max(Query(ql, m, L, m, o * 2), 
                   Query(m+1, qr, m+1, R, o * 2 + 1));
    }
}

扣的

練習題

而題目也可以換成區間和

查詢 \(a[l]\) 到 \(a[r]\) 的總和

怎麼做?

把剛剛的線段樹的 \(\max\) 操作

換成加法就好了!

只要是可以疊加的東西

線段樹都可以存

  • 最大值、最小值

  • 最大公因數

  • 區間和

  • 矩陣

  • etc.

單點修改

如果要你同時支援兩種操作：

  1. 查詢 \(a[l]\) 到 \(a[r]\) 的總和

  2. 修改一個點 \(a[i]\) 的值

那就在線段樹上做修改ㄅ

21

12

9

5

7

5

4

\([1, 6]\)

\([1, 3]\)

\([4, 6]\)

\([1,2]\)

\([3]\)

\([4, 5]\)

\([6]\)

6

1

\([1]\)

\([2]\)

3

2

\([4]\)

\([5]\)

\(a:\{1,6,5,2,3,4\}\)

\(8\)

21

9

5

8

11

15

27

一直遞迴到區間剩一個點

void Modify(int p, int v, int l, int r, int o){
    if(l == r){
        sgt[o] = v;
        return;
    }
    int m = (l + r) / 2;
    if(p <= m) Modify(p, v, l, m, o * 2);
    else Modify(p, v, m+1, r, o * 2 + 1);
    sgt[o] = sgt[o * 2] + sgt[o * 2 + 1];
}

把 \(a[p]\) 修改成 \(v\)

總共會經過 \(\log N\) 個點，

複雜度 \(\mathcal{O}(\log N)\)

一個更難的問題：

如果要把 \(a[i]\) 到 \(a[j]\) 全部加上 \(x\) ?

直接的想法：

把 \(i\) 到 \(j\) 全部拆成單點修改

複雜度會掉到 \(\mathcal{O}(N \log N)\)，完全不理想

每次把完整覆蓋區間的修改存下來，

等到要查詢該區間，

或者再次修改時，

再「真正」的修改那個區間

懶人標記 Lazy Tag !

21

12

9

5

7

5

4

\([1, 6]\)

\([1, 3]\)

\([4, 6]\)

\([1,2]\)

\([3]\)

\([4, 5]\)

\([6]\)

6

1

\([1]\)

\([2]\)

3

2

\([4]\)

\([5]\)

\(a:\{1,6,5,2,3,4\}\)

操作:

把 \([3,5]\) 項加上 \(3\)

8

3

11

15

30

15

7

4

\([1, 6]\)

\([1, 3]\)

\([4, 6]\)

\([1,2]\)

\([3]\)

\([4, 5]\)

\([6]\)

6

1

\([1]\)

\([2]\)

3

2

\([4]\)

\([5]\)

\(a:\{1,6,5,2,3,4\}\)

操作:

查詢 \([2,4]\) 項的和

8

3

11

15

30

15

30

15

15

7

8

11

6

7

4

\([1, 6]\)

\([1, 3]\)

\([4, 6]\)

\([1,2]\)

\([3]\)

\([4, 5]\)

\([6]\)

6

1

\([1]\)

\([2]\)

3

2

\([4]\)

\([5]\)

\(a:\{1,6,5,2,3,4\}\)

操作:

查詢 \([2,4]\) 項的和

8

5

11

15

30

15

30

15

15

7

8

11

6

6

5

歸納懶人標記的特性

  • 如果一個修改完整覆蓋一個節點，我們可以用節點的長度來推出節點的新長相 (區間和)，並且打標記在這個節點
  • 在往後查詢或是修改時，需要先把節點的標記往下推給子節點，才能更新到子節點的資訊
  • 把區間修改的複雜度降到 \(\mathcal{O}(\log n)\) !

PUSH!

把懶標下推

int sgt[N * 4]={};
int laz[N * 4]={};
void push(int l, int r, int o){
    if(laz[o] == 0) return;
    
    int m = (l + r) / 2;
    
    sgt[o * 2] += (m - l + 1) * laz[o];
    laz[o * 2] += laz[o];
    
    sgt[o * 2 + 1] += (r - m) * laz[o];
    laz[o * 2 + 1] += laz[o];
    
    laz[o] = 0;
}

扣的細節

int sgt[N * 4]={};
int laz[N * 4]={};
void push(int, int, int);

void Modify(int ql, int qr, int x, int L, int R, int o){
    if(ql <= L && R <= qr){
        sgt[o] += (R - L + 1) * x;
        laz[o] += x;
        return;
    }
    push(l, r, o);
    int m = (L + R) / 2;
    if(qr <= m){
        Modify(ql, qr, x, l, m, o * 2);
    }
    else if(ql > m){
        Modify(ql, qr, x, m+1, r, o * 2 + 1);
    }
    else{
        Modify(ql, m, x, l, m, o * 2);
        Modify(m+1, qr, x, m+1, r, o * 2 + 1);
    }
    sgt[o] = sgt[o * 2] + sgt[o * 2 + 1];
}

int Query(int ql, int qr, int L, int R, int o){
    if(ql <= L && R <= qr){
        return sgt[o];
    }
    push(l, r, o);
    int m = (L + R) / 2;
    if(qr <= m){
        return Query(ql, qr, L, m, o * 2);
    }
    else if(ql > m){
        return Query(ql, qr, m+1, R, o * 2 + 1);
    }
    else{
        return Query(ql, m, L, m, o * 2) + 
               Query(m+1, qr, m+1, R, o * 2 + 1);
    }
}

要注意 push 的位置!

練習題~~

一些變化的題目:D

APCS / ZJ f315 - 4. 低地距離

給你 \(2n\) 個數字的序列，\(1\) 到 \(n\) 各出現兩次

定義 \(L(x)\) 為兩個 \(x\) 之間比 \(x\) 小的數字數量

求 \(\sum_{i=1}^{n} L(i)\) ?

Hint：區間和 \(=\) 前綴 \(-\) 前綴

\(1 \leq n \leq 10^5\)

TIOJ 1224 - 矩形覆蓋面積

給你很多個平面上的矩形，

求出所有矩形的聯集面積?

\(N \leq 10^5, \\ 0 \leq x_i, \ y_i \leq 10^6\)

TIOJ 1408 - 我很忙

給你 \(N\) 個時段 \([A_i, \ B_i)\)，其中該時段至少要有 \(C_i\) 單位的時間要是忙碌的，求最少有多少單位時間是忙碌的?

\(1 \leq N \leq 10^5\)

\(0 \leq A_i, \ B_i, \ C_i \leq 10^5\)

IOI 2013 / TIOJ 1836

給你一個 \(N \times M\) 的盤面，一開始所有數字預設為 \(0\)

你需要支援兩種操作：

  • 把座標位於 \((P, Q)\) 的值改成 \(K\)

  • 查詢以 \((P, Q)\)、\((U, V)\) 畫成的矩形中所有數字的最大公因數

\(1 \leq N, \ M \leq 10^9\)

\(0 \leq K \leq 10^{18}\)

遊戲 Game

其他不重要的補充

: O

迭代型線段樹

實在是有人覺得遞迴型態的線段樹常數太大(X

所以就發明了用迴圈就能跑的線段樹

還可以把陣列大小壓到 \(2N\)，懶標大小壓到 \(N\)

毒瘤中的毒瘤ww

可以參考：蛋餅Orz

動態開點線段樹

例如值域線段樹

沒有用到的節點就直接不開空間

等到用到時再開新節點，會省很多空間(X)

實作的部分就要用指標才行

持久化線段樹

有興趣的自己去查w

耶

線段樹

By youou

Made with Slides.com

線段樹

  • 296

More from youou