基礎DP 3
yungyao
背包問題
Knapsack problem is harder than FFT
FHVirus
很難的問題(According to FHVirus)
沒啦其實還好
很簡單ㄉ:)
What is 背包
給你\(n\)個東西，和一個可以乘載量為\(m\)的袋子
每個東西有重量 \(p_i\) 和價值 \(w_i\)
問你最大的價值為何
想greedy他?
(用CP值排序)
想想這個狀況
\(n = 3, m = 6\)
\(p_1 = 4, w_1 = 5\)
\(p_2 = 3, w_2 = 3\)
\(p_3 = 3, w_3 = 3\)
最佳解是取 \(p_2,p_3\)
但用CP值會只取到 \(p_1\)
定義一下DP
我們可以定義
\(dp[i][j]\) 為取前 \(i\) 個東西，使用 \(j\) 個背包空間時
可以獲得的最大價值
那轉移式就會是
\(dp[i][j] = max(dp[i-1][j],dp[i-1][j-p_i] + w_i)\)
也就是說，對於每個空間用量，你可以選了第\(i\)個東西或不選
Code
//Knapsack DP code
//n is number of items, m is maximum knapsack capacity
//p for price, w for weight
int dp[maxn][maxn];
int n, m;
cin >> n >> m;
for (int i=1;i<=n;++i){
int p, w;
cin >> p >> w;
for (int j=0;j<p;++j) dp[i][j] = dp[i-1][j];
for (int j=p;i<=m;++j) dp[i][j] = max(dp[i-1][j], dp[i-1][j - p] + w);
}
cout << dp[n][m];滾一下
此時你又可以發現，轉移式在轉移到\(dp[i][j]\)時
只會用到\(dp[i-1]\)的資料
因此你可以只要維護當前的\(dp[i]和dp[i-1]\)就好
同時取\(dp[i][j]\)時
你也只需要取 \(dp[i-1][k] s.t. k \leq j\)的資料
因此如果你讓for迴圈從 \(j=k\) 開始遞減
你可以只需要維護\(dp[j]\)就好
Code
//Knapsack DP code
//n is number of items, m is maximum knapsack capacity
//p for price, w for weight
int dp[maxn];
int n, m;
cin >> n >> m;
while (n--){
int p, w;
cin >> p >> w;
for (int i=m;i>=p;--i) dp[i] = max(dp[i], dp[i - p] + w);
}
cout << dp[m];複雜度
你會發現有\(n \times m\)個轉移點
而轉移花費為\(1\)
因此總複雜度為\(O(nm)\)
奇怪的背包
剛剛上面講得基本上是指01背包問題
但其實還有很多種背包
etc:
有限背包, 無限背包
不過作法其實都是一樣的概念
但在細節上有差異，可以自己想想怎麼做
(還有可分割背包, 大數背包這種跟DP比較沒關係的類似題)
例題
裸ㄉ
實作一下剛剛講的東東就好ㄌ
懶得打ㄌ(X
現在變成有好幾個group
每個group中只能選一個
小小變化一下
除了預算
還多了總量限制ㄛ
給你\(n\)個正整數
問你能不能讓某些數變成負的
使所有數加起來是\(0\)
\(n \leq 100, a_i \leq 1000\)
難難ㄉDP
提示一下，可以用帕斯卡三角形取\(C\)
有 \(n\) 個單字，每個單字有長度 \(l_i\) 跟韻種 \(c_i\)
現在你想要寫出一首 \(m\) 行，每行長度均為 \(k\) 的詩
其中某些行的尾字的韻種必須相同
求有幾種可能的詩
矩陣快速冪
快速冪
大家還記得吧
好我當作大家記得
矩陣乘法
高二下才會教
但你現在就得先學了
what is 矩陣乘法
先說，為什麼他會長這樣要牽扯到矩陣的定義
但我們先不談，數學老師自然會講
我們若有個 \(n \times m\) 的矩陣 \(A\)，和\( m \times p \)的矩陣 \(B\)
則 \(A \times B\) 為 \(n \times p\) 的矩陣
其中，矩陣\( A,B \)可相乘若且唯若 \(A_{col} = B_{row}\)
(以上面為例就是那個 \(m\) 是一樣的)
詳細一點
我們直接示範看看
總之設 \(A,B\) 可相乘，令 \(A \times B = C\)
則 \(C_{ij} = \sum\limits^{A_{col}}_{k=1}A_{ik} \times B_{kj}\)
複雜度
矩陣乘法複雜度為 \(O(n^3)\)
但矩陣快速冪題目的矩陣通常不會太大
不過還是要注意一下
矩陣乘法+快速冪
我們這邊先省略掉數學證明
總之矩陣乘法存在結合律
而且也可以對方陣取 \(n\) 次方
所以如果我們將DP式轉為一個矩陣
就可以好好的做了
題敘大致上是說：有6種西洋棋子可以用
每種棋子都有無限多個
你要取 \(n\) 個棋子排成一列
而國王跟皇后都必須取偶數個
求排列方法數模\(10^8+7\)
\(n \leq 10^9\)
先想想看 O(n) 作法
分三種狀態
- 國王跟皇后都有偶數個
- 國王跟皇后一奇一偶
- 國王跟皇后都有奇數個
轉移式呢？
\(dp[n][1] = 4 \times dp[n-1][1] + dp[n-1][2]\)
\(dp[n][2] = 2 \times dp[n-1][1] + 4 \times dp[n-1][2] + 2 \times dp[n-1][3]\)
\(dp[n][3] = dp[n-1][2] + 4 \times dp[n-1][3]\)
數學表達
令\(dp[n-1][1] = a,dp[n-1][2] = b,dp[n-1][3] = c\)，則
dp_n = \begin{bmatrix} 4 & 1 & 0 \\ 2 & 4 & 2 \\ 0 & 1 & 4 \end{bmatrix} \times \begin{bmatrix} a \\ b \\ c \end{bmatrix} = \begin{bmatrix} 4a + b \\ 2a + 4b + 2c \\ b + 4c \end{bmatrix}
數學表達
我們可以發現，每次往下一項走，都是再乘一次矩陣
所以我們可以把他轉成矩陣的 \(n\) 次方
dp_n = \begin{bmatrix} 4 & 1 & 0 \\ 2 & 4 & 2 \\ 0 & 1 & 4 \end{bmatrix}^n \times \begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix}
矩陣快速冪丟下去
總而言之
矩陣快速冪可以使用的條件就是
我們的DP轉移式是取固定的狀態
而且都是把那些狀態的值乘上一個常數然後加起來
就能用矩陣快速冪做
恭喜你ACㄌ
例題
給定 \(f_1, f_2, a, b\)
令 \(f_n = bf_{n-1} + af_{n-2}\)
求 \(f_n (n \leq 10^9)\)
給一張圖，\(V \leq 100,E \leq 50000\)，可能有重邊
給定一個起點和終點
求恰好經過 \(k\) 條邊的路徑有多少條
(路徑不需要簡單，也就是你一個邊或點走多少次都沒關係)
\(k \leq 10^{15}\)
有一個大小為 \(n\) 的陣列
我們定義一個好的序列為
該序列每個相鄰的項的XOR值均為 \(3\) 的倍數
且序列裡的每一項都在陣列中出現過
求有幾種長度為 \(k\) 的好的序列
\(n \leq 100, k \leq 10^{18}\)
我賽中不會寫QQ
小補充
位元DP
沒la哈哈，我有乖乖做簡報
- 一般狀態壓縮DP
- \(3^n\) DP（枚舉子集）
- SOS DP
輪廓線DP
狀態壓縮 DP
把狀態用01序列表示
在一張帶權完全圖上
找出經過所有點且權重最小的路徑
NP-Hard
狀態壓縮
我們可以將所有可能的狀態枚舉
在這題中，狀態就是每個點是否被走過了
0
1
5
2
3
4
狀態：\(010110_2\)
狀態：\(22_{10}\)
DP狀態
我們可以定義 \(dp[mask][i]\)
\(mask\) 表示被遍歷過的點
\(i\) 則表示最後停留在哪
DP式？
定義點 \(i\) 到點 \(j\) 的邊權為 \(w(i, j)\)，則
\(dp[mask][i]\)
\( = \min\limits_{j \in mask\setminus i} dp[mask \setminus i][j] + w(j, i)\)
這條式子表示在遍歷過 \(mask\) 內的點，且結束在 \(i\)
轉移來源就會是那些在遍歷過 \(mask \setminus i\) 的點
而不管結束在哪，都是可能的轉移來源
數線上 \(1 \sim n\) 每個點有一個地鼠洞
第 \(i\) 個點的地鼠每 \(t_i\) 秒會冒出來一次
玩家每秒可以走一單位
從 \(0\) 出發，求所有地鼠都打到至少一次至少要花多少時間
\(n \leq 16\)
有 \(n\) 個人要搭電梯，電梯載重量最大為 \(x\)
每個人的體重是 \(w_i\)
至少要幾趟電梯才能載完所有人
\(n \leq 20, 1 \leq \forall w_i \leq x \leq 10^9\)
在一個 \(n \times n\) 的表格上
每一排跟列都恰選一個值
求乘積最大值
\(n \leq 20\)
枚舉子集DP
在上面的題目中
枚舉 \(mask\) 其實就是在枚舉集合（複雜度 \(2^n\)）
然而有時候我們需要對於所有集合
再去枚舉他的子集
可以把 \(n\) 個人分成任意組別
若第 \(i\) 個人和第 \(j\) 個人在同一組會獲得 \(a_{ij}\) 分
求最大分數
\(n \leq 16, |a_{ij}| \leq 10^9\)
好用的式子
枚舉 \(mask\) 的子集
//mask 是現在的集合
for (int submask = mask;submask != 0;submask = (submask - 1) & mask){
//在這邊操作
}複雜度?
枚舉集合的複雜度顯然是 \(2^n\)
而對於枚舉集合的子集複雜度也是 \(2^{|set|}\)
乍看之下複雜度會是 \(4^n\)
但實際上，我們把式子用二項式定理拆開，就會發現其實是
\(\sum\limits_{i=0}^n C^n_i \times 2^i\)
\(= C^n_0 \times 2^0 + C^n_1 \times 2^1 + C^n_2 \times 2^2 + ... + C^n_n \times 2^n\)
\(= (2 + 1)^n = 3^n\)
於是我們如果好好枚舉子集，那複雜度其實只有 \(O(3^n)\)
SOS DP
I need help DP
Sum Over Subsets DP
SOS DP
對於每一個 \(mask\)
\(dp[mask]\) 表示 \(mask\) 的子集和
中國人也把SOS DP叫做多維前綴和
SOS DP樹狀圖
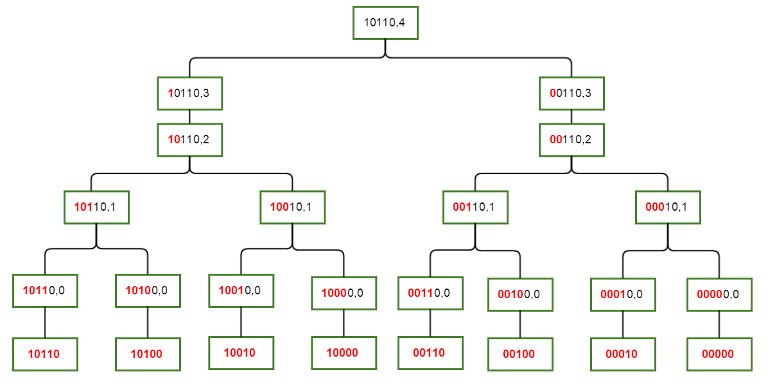
Code
int dp[1 << maxn], n;
for (int i=0;i<n;++i){
for (int mask=0;mask<1<<n;++mask) if ((mask >> i) & 1){
dp[mask] += dp[mask ^ (1 << i)];
}
}可以當黑盒子用就好
之後再慢慢理解
每個 \(mask\) 的內容
我們可以觀察到
每個 \(mask\) 在DP完全跑完後
\(dp[mask]\) 即會代表 \(mask\) 所有子集的和
有 \(n\) 個數字 \(a_1, a_2, ..., a_n\)
對於每個數字 \(a_i\)，你想找出是否存在一個另一個數\(a_j\)
使的\(a_i \text{ AND } a_j = 0\)
對於第 \(i\) 個數
如果存在 \(a_j\) 的話即輸出 \(a_j\)，不存在則輸出 \(-1\)
有 \(n\) 個由前 \(24\) 個字母組成的三字元長單字
我們定義只要一個字內至少有一個字元為母音
該單字就是合法的
對於所有 \(2^{24}\) 個可能的母音集合
你想求出分別會有幾個單字是合法的
為方便輸出，只要輸出每個答案的平方\(XOR\)和即可
\(n \leq 10^4\)
小補充
三個好用的函式
- lowbit: x & -x
- highbit: __lg(x)
- bits count: __builtin_popcount(x)
參考資料
DP3
By yungyao
DP3
DDDDDDDPPPPPPP
