数値解析学から見た非逐次データ同化
宮武勇登 (大阪大学)
MfIP連携探索ワークショップ
数学を軸とする新たな価値創造に向けて
簡単な自己紹介〜数値解析を軸に〜
構造保存数値解法 （Geometric Integration）
数値線形代数 （連立一次方程式など行列に関する計算）
不確実性定量化 （UQ: Uncertainty Quantification）
科研費：数値代数解析学の開拓 ー量子系偏微分方程式の数値解法の新展開ー
科研費：データ同化の信頼性向上に向けた時間逆向き数値計算法の確立と地震学への応用展開
東大地震研特定共同研究：深層学習とデータ同化の協働による固体地球科学の深化
- 発展方程式の持つ数理構造を離散化後も再現する数値解法
- 現在では広く様々な分野に浸透 （近年は深層学習との組み合わせもある）
- ほとんどの数値計算における要素技術だが「万能解法」はない
- 離散的な問題を連続化して考えることもある
- データ同化では，手法の信頼性/不確実性の定量的評価が重要
- 数値計算の誤差も不確実性の一種
さきがけ：発展方程式の数値計算に対する不確実性定量化理論の創出
数値解析
古くからあるかなり成熟した研究分野
今日お話したいこと
データ同化（固体地球科学）の研究者と連携すると
多くの新しい（とても面白い）問題設定があふれている
どんなことができるようになったか... というよりも
どういう経緯で，どんなテーマ（2例）が生まれたか
研究の時系列
2015年：学位取得
副査：長尾大道 先生 （東大地震研）
地震の研究における数値計算の話を聞く
2017年頃〜
伊藤伸一氏 （東大地震研），松田孟留氏（東大情報理工）と
あれやこれやと議論を始める
その後，徐々に理解が進み，共同研究スタート
酸ヶ湯のアメダス
最初は，何が課題か全く分からなかった
逐次データ同化
逐次データ同化 と 非逐次データ同化
主に離散的なモデルを用いて，最新のデータが得られている時刻の変数を推定
非逐次データ同化
連続的なモデル（一般には空間3次元の時間発展PDE）を用いて，
初期時刻の変数を推定
データ同化
シミュレーションと観測を組み合わせ，
より適切な予測などを行う数理手法
気象予測
非逐次データ同化の応用例
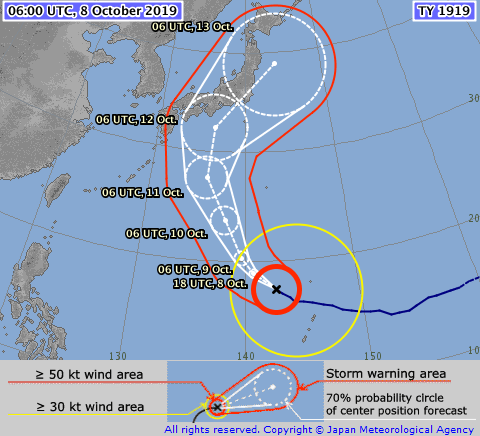
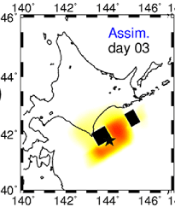
地震
材料科学
（気象庁）
（Kano et al. 2015）
（伊藤伸一先生のweb）
伊藤伸一氏（東大地震研）
きっかけ
非逐次データ同化に現れる 「2nd-order adjoint方程式」，どう計算すべき？
\( \displaystyle \frac{\mathrm d}{\mathrm dt} {\color{blue}\bm{\xi}(t)} = - (\nabla _{\bm{x}} \bm{f}(\bm{x}(t))^\top {\color{blue}\bm{\xi}(t)} - (\nabla_{\bm{x}}(\nabla_{\bm{x}} \bm{f}(\bm{x}(t)))\bm{\delta}(t))^\top \bm{\lambda}(t)\)
注意： \( \bm{x}(t), \ \bm{\delta}(t), \ \bm{\lambda}(t)\) は別の微分方程式の解
この方程式を，「終端条件」を課して「時間逆向き」に解きたい
- 線形な方程式だし，時間逆向きに解くこと自体が難しいのではない
- \( \bm{x}(t), \ \bm{\delta}(t), \ \bm{\lambda}(t)\) の数値計算とセットで考える必要がある
- やみくもに高精度計算すればよいわけではない
モデル：
4次元変分法（4D-Var）
\(\displaystyle \frac{\mathrm d}{\mathrm dt} \bm{x}(t) = \bm{f}(\bm{x}(t)), \quad \bm{x}(0) = {\color{blue}\bm{\theta}}\)
観測：
\(\displaystyle D = \{ \bm{d}_1,\bm{d}_2,\dots \} \) (\(\bm{d}_k = \bm{h}(\bm{x}(t_k)) + \bm{\omega}_k \) )
4D-Var：
事後分布から（マップ解などの）情報を抽出
\( \displaystyle p(\bm{\theta}\mid D) \propto p(\bm{\theta}) \prod_{k\in T_{\mathrm{obs}}} q (\bm{d}_k - \bm{h} (\bm{x}(t_k;\bm{\theta})))\)
\( \displaystyle \tilde{p}(\bm{\theta}\mid D) \propto p(\bm{\theta}) \prod_{k\in T_{\mathrm{obs}}} q (\bm{d}_k - \bm{h} ({\color{blue}\bm{x}_k(\bm{\theta})}))\)
- 一般には空間3次元の発展方程式
- 重要なのは，「発展方程式」であること
実際に計算する際には，厳密解は近似解（数値解）で置き換える
（観測のノイズ以外の）不確実性たち
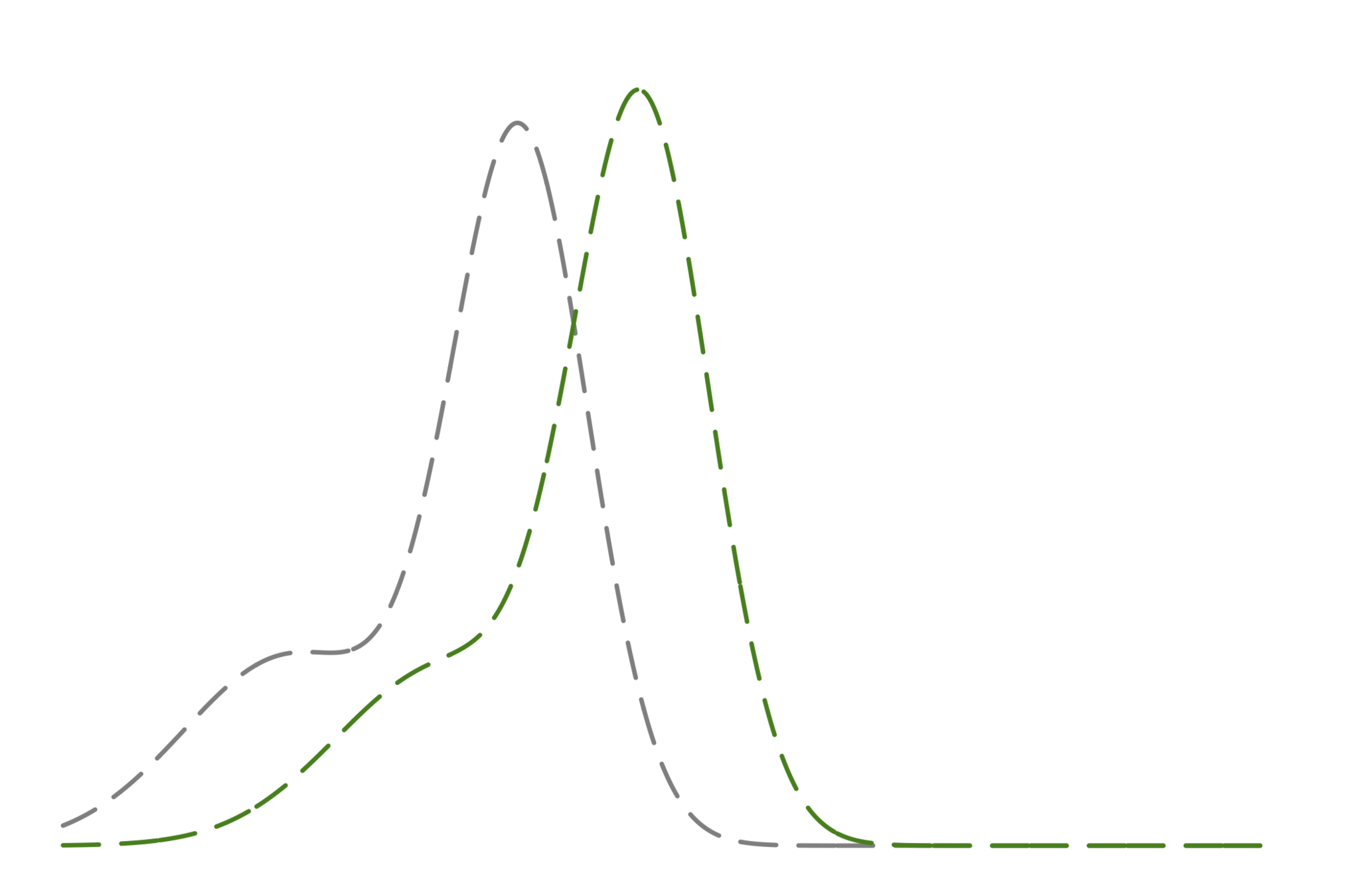
様々な事後分布たち
もし真のモデルが使えるならば
（未知）
使用しているモデルに対して
厳密解が使えるならば
（未知）
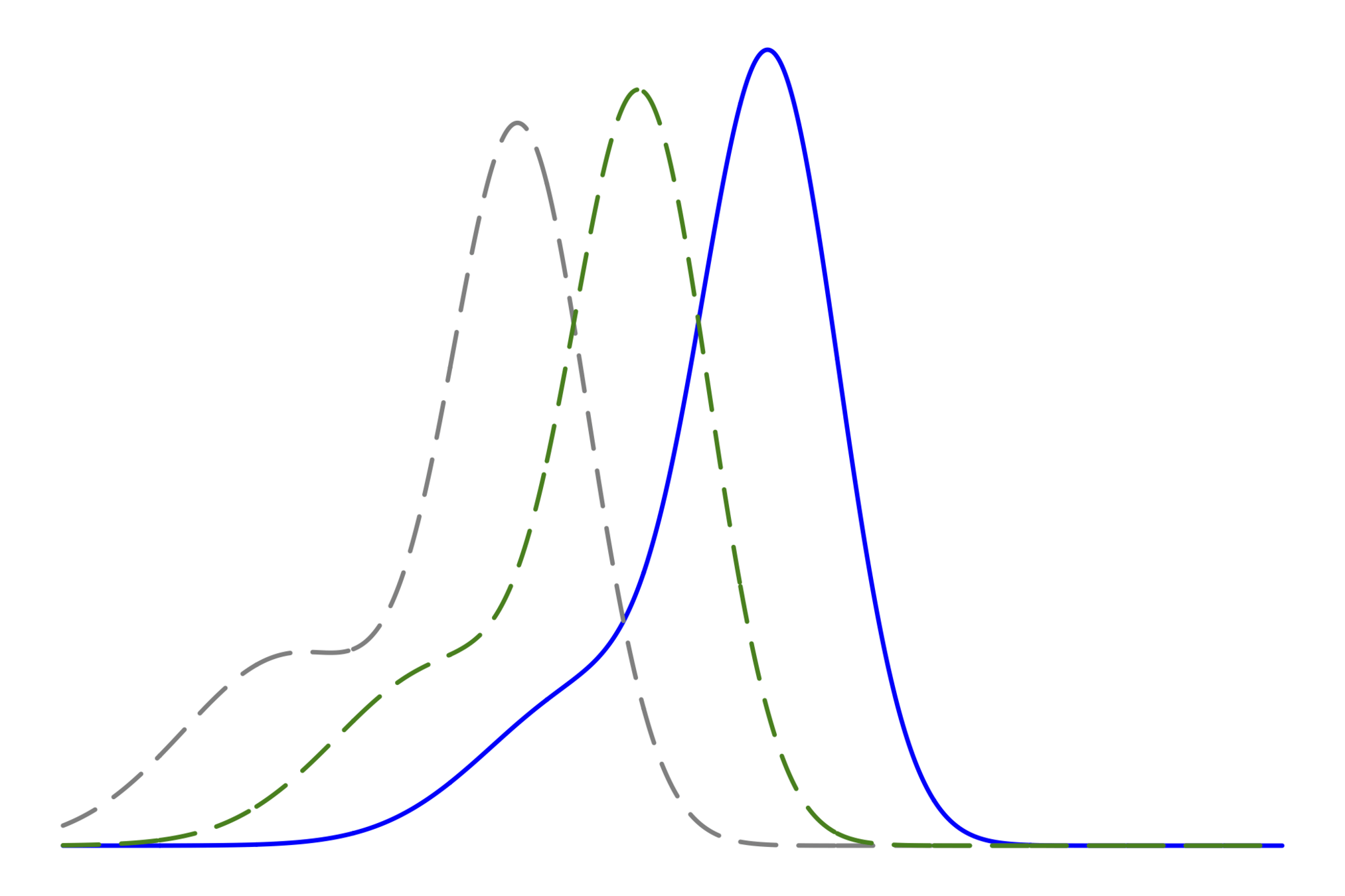
使用しているモデルに対して
近似解を使った場合
（原理的には計算可能）
事後分布をガウシアンで近似
（原理的には計算可能）
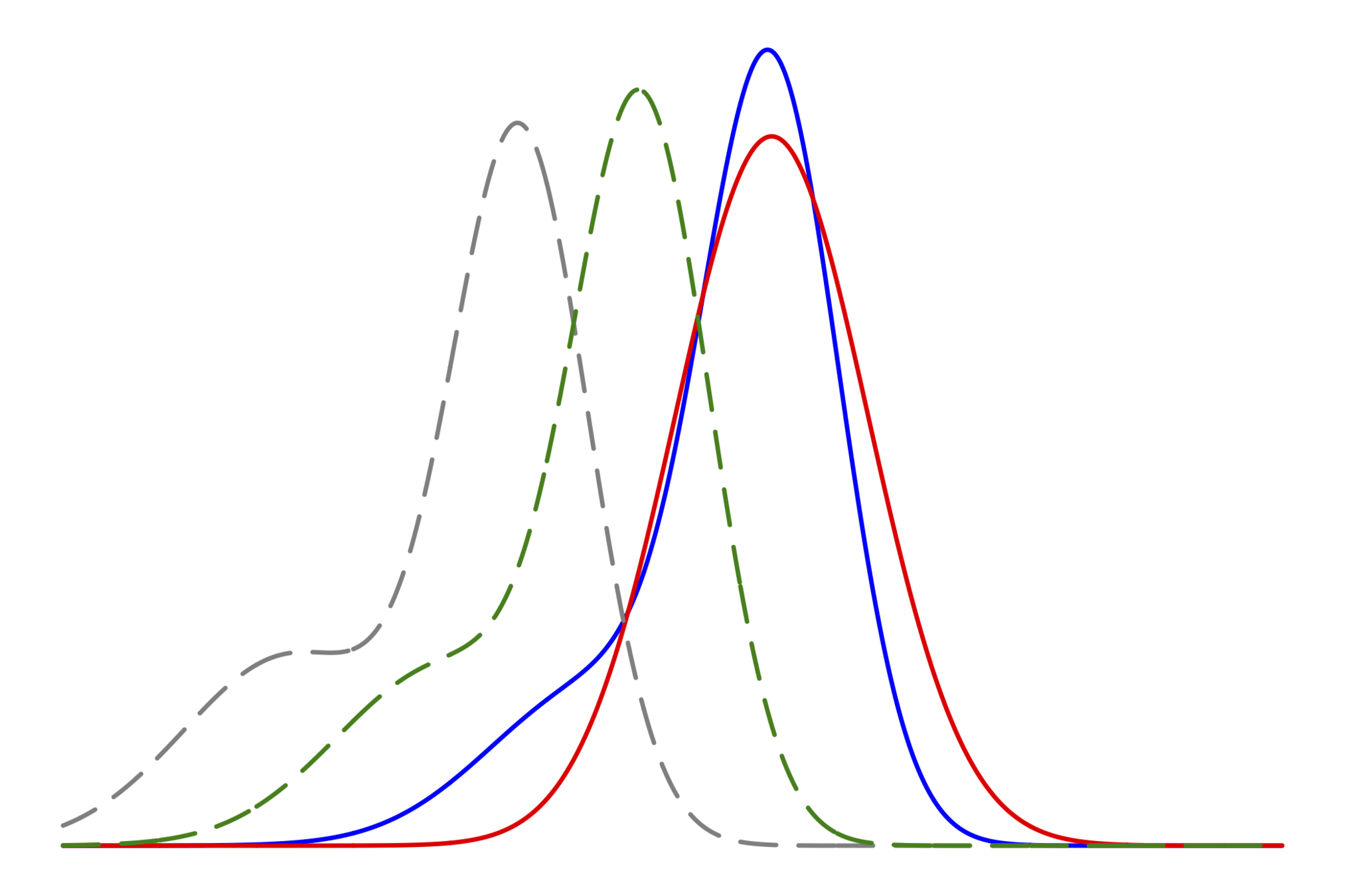
最初の課題
ガウシアンの分散 の（成分の）計算をするために
とある連立一次方程式を解く必要があり，
そのためには，行列ベクトル積の計算が必要で，
そのためには，2nd-order adjoint方程式の計算が必要だが，
"高精度"に計算するにはどうすればよいか？
もし真のモデルが使えるならば
（未知）
使用しているモデルに対して
厳密解が使えるならば
（未知）
使用しているモデルに対して
近似解を使った場合
（原理的には計算可能）
事後分布をガウシアンで近似
（原理的には計算可能）
（注） こんなふうに，「この計算をなんとかしたい！」
というご相談が多い
この計算の不確実性が
一番大きいかもしれない
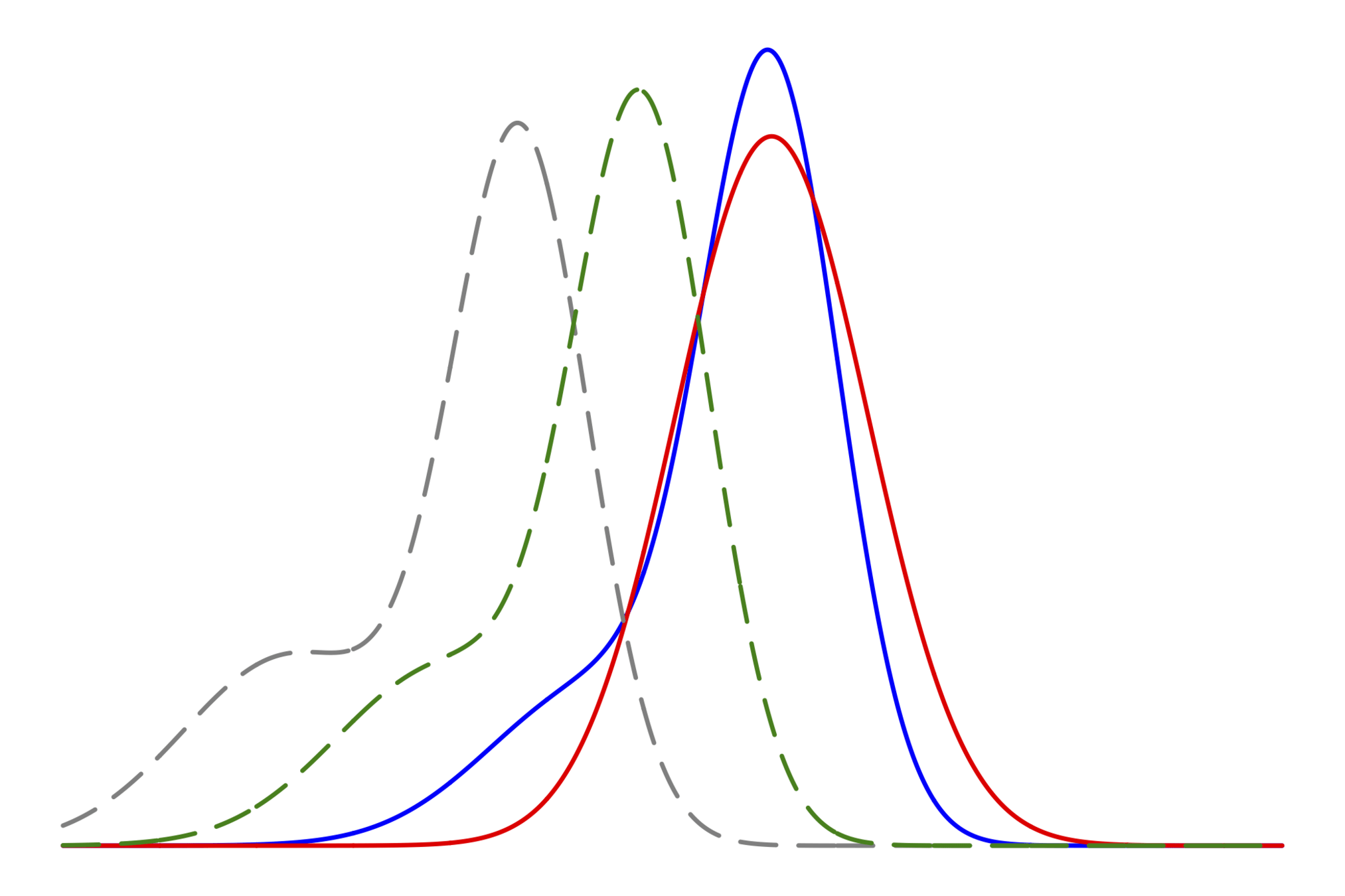
徐々に気になってきたこと
- どのくらいの精度で分散を求めたい？
- 他の不確実性の大きさが一つの指標になるのでは？
- 青と緑の差も気になる
- 実は，行列ベクトル積に限れば厳密に計算できるが，
- それと分散の計算の精度は別問題
もし真のモデルが使えるならば
（未知）
使用しているモデルに対して
厳密解が使えるならば
（未知）
使用しているモデルに対して
近似解を使った場合
（原理的には計算可能）
事後分布をガウシアンで近似
（計算可能）
2つの数値解析的課題
使用しているモデルに対して
近似解を使うことの影響
事後分布をガウシアンで近似したときの
分散の計算
松田さんと共同研究
伊藤さん・松田さんと共同研究
よくあるご批判
数値計算の誤差の影響を定量的に評価したい
数値計算の誤差が無視できるようなアルゴリズムを作るのが
数値解析学者の仕事 ！！
それはそう （そういう研究もやっている）
しかし
- 難しいものは難しいこともある
- リソースを使いまくるのもよくない （電気代問題）
- 必要以上の精度で計算するのも考えもの（電気代問題）
使用しているモデルに対して
近似解を使うことの影響
M. 2024
A new family of fourth-order energy-preserving integrators
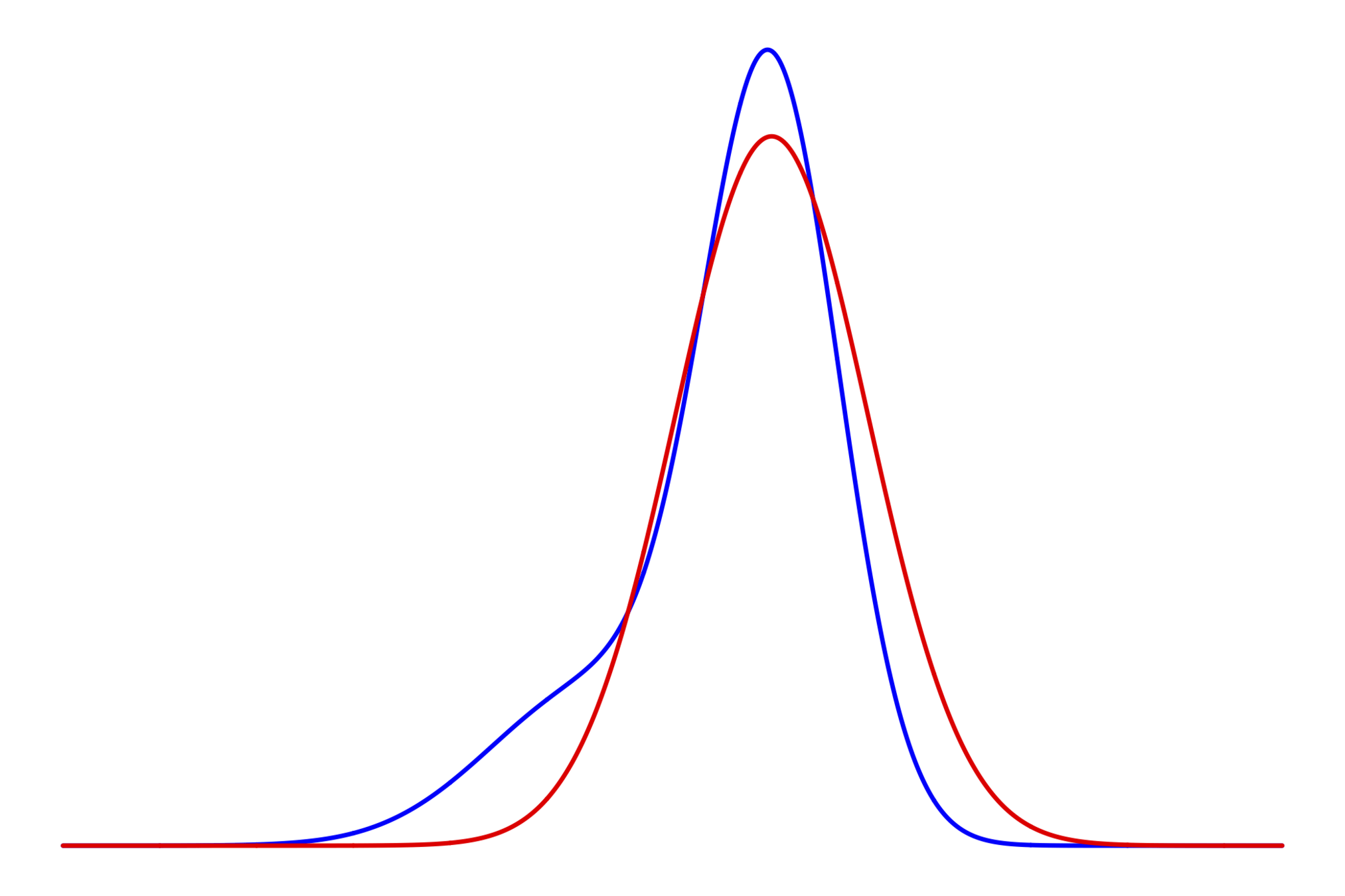
調和振動子 （ベイズ推定ではなく，最尤推定の例）
そう簡単ではない
\displaystyle \min_{\theta\in\Theta} \sum_{n=1}^N \| Hx(t_n;\theta)-y_n\|^2
\displaystyle \min_{\theta\in\Theta} \sum_{n=1}^N \| H\widehat{x}(t_n;\theta)-y_n\|^2
Ideal
Reality (use approx. sol.)
\(\hat{\theta}_{\mathrm{ML}}\)
\(\hat{\theta}_{\mathrm{QML}}\)
バイアス： \( \mathrm{E}_{\theta} [\hat{\theta}_{\mathrm{QML}}] - \theta \neq 0\)
最小二乗誤差（mean squared error）： \( \mathrm{E}_{\theta} \big[\|\hat{\theta}_{\mathrm{ML}}-\theta\|^2\big] \) vs \( \mathrm{E}_{\theta} \big[\|\hat{\theta}_{\mathrm{QML}}-\theta\|^2\big] \)
MLE
Runge–Kutta
中点則
【考察】
数値計算の精度によって，
推定の性能は大きく異りうる
青や赤の振る舞いを研究する論文は
ほとんどない
誤差 \( = \) \( \| \) 厳密解 \( - \) 近似解 \( \|\) \(\leq\) error bound
数値解析理論では難しい
厳密な不等式評価より
「だいたい」で評価できた方が有用？
もちろん，統計的に然るべき議論
e.g. \( C (\Delta t)^p \)
実際の "値" には大きなギャップ
何桁も違うかもしれない
- これ自体はとても有益な情報
- 一方で，タイトに定量的に評価するには
近似計算する以上に難しい
こんなことができると嬉しそう
使用しているモデルに対して
厳密解が使えるならば
（未知）
使用しているモデルに対して
近似解を使った場合
（原理的には計算可能）
- せめて，近似計算の影響でずれた分くらい，
事後分布の幅も適切に広くなってほしい - できれば，（例えば）MAP解の位置も改善したい
数値計算のUQ
（従来型の）数値解析
数値計算のUQ
計算前に定性的評価
計算後に定量的評価
関数解析など
確率・統計
いつ評価？
主要な道具
【私見】 数値解析の一トピックとみなしてもよい気がします
数値解析の指す範囲は時代とともに変遷してきた
近似誤差の影響の定量化のアイデア
誤差（同じことだが近似解）を確率変数でモデリング
ならば，分布を見れば誤差の定量化と言えそう
- 各時刻の分布がRunge-Kutta法などの近似解
- 広がり （分散） が誤差の定量化 （であることの数学的な説明）
- このような分布を高速に計算できる
たとえば
現状：いくつかのアイデアが提案されているが，「決定版」はないし，数学的な説明は依然として不十分
様々な定量化アプローチ
フィルタ型
摂動型
単調回帰型 （松田孟留さんたちとの共同研究） ：逆問題専用
パッケージの開発も重要
- 摂動を加えながら時間発展
- 各時刻でヒストグラムから数値解の
信頼度を定量化 - ただし，絶対的な根拠があるわけではない
- 予測（\(\Delta t\) 時間発展） と修正を繰り返す
- カルマンフィルタがベース
- 近似解と観測データから誤差の影響を定量化
- 誤差に対して，定性的な仮定を置く
- 単調回帰やより一般に制約付き最適化問題を解く
まだ研究途中だけど...
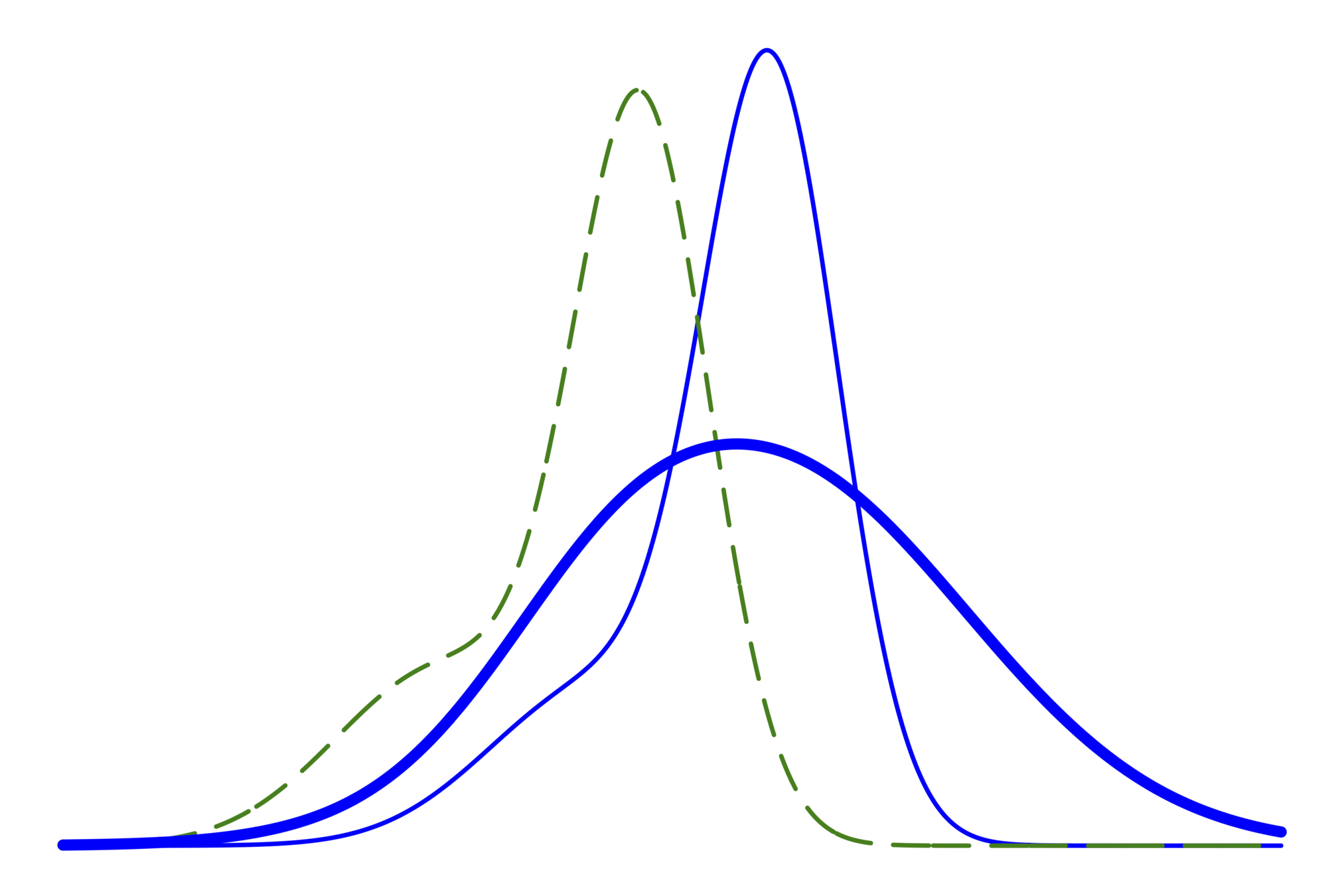
太い青相当の事後分布
- Matsuda, M. (2021)
Estimation of ordinary differential equation models with discretization error quantification - Matsuda, M. (2023)
Piecewise monotone estimation in one-parameter exponential family - Marumo, Matsuda, M. (2023)
Modelling the discretization error of initial value problems using the Wishart distribution
2つの数値解析的課題
使用しているモデルに対して
近似解を使うことの影響
事後分布をガウシアンで近似したときの
分散の計算
松田さんと共同研究
伊藤さん・松田さんと共同研究
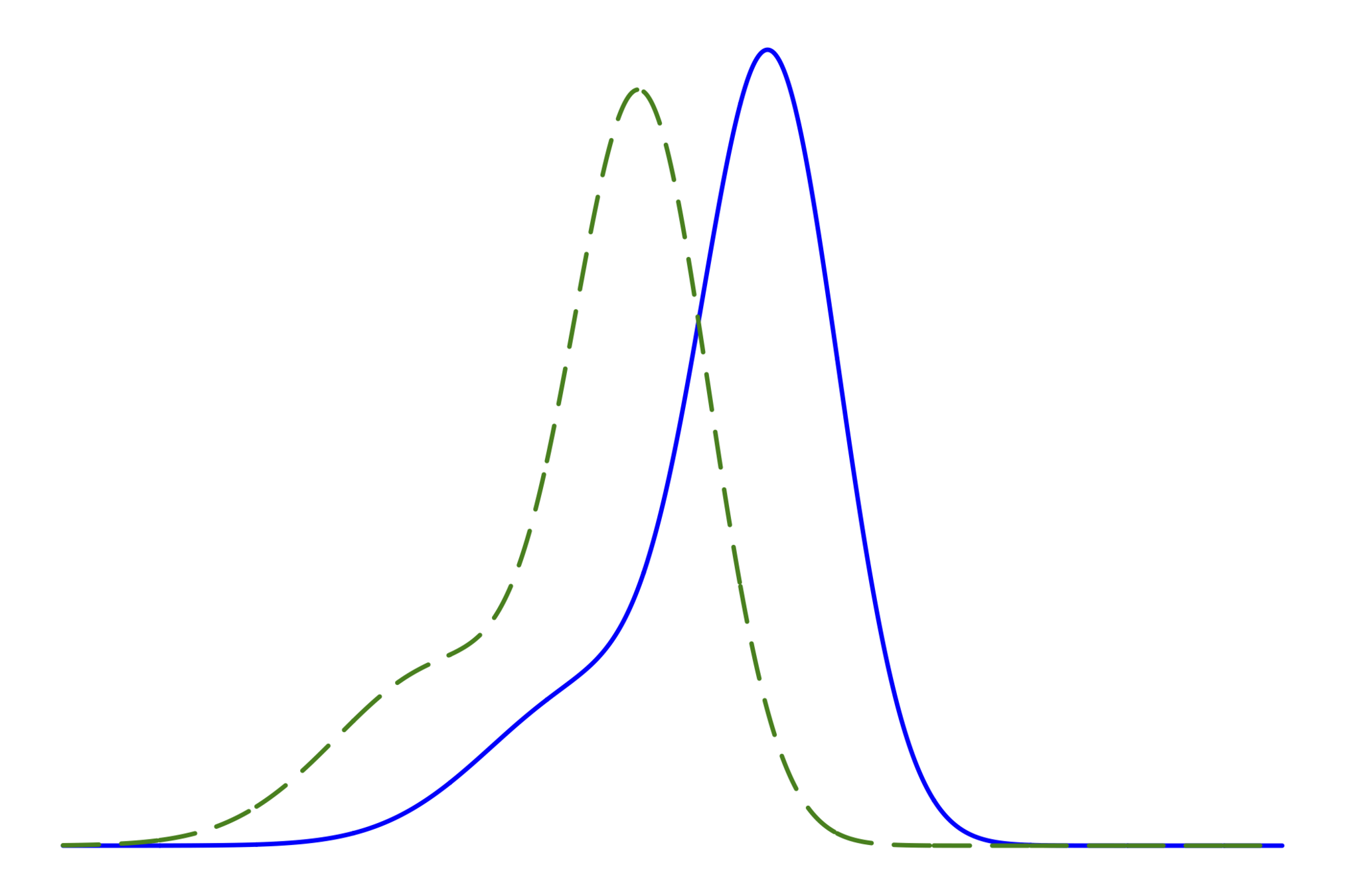
計算したいのは，青の山の位置と赤の分散
問題設定
使用しているモデルに対して
近似解を使った場合
（原理的には計算可能）
事後分布をガウシアンで近似
（計算可能）
モデル：
\(\displaystyle \frac{\mathrm d}{\mathrm dt} \bm{x}(t) = \bm{f}(\bm{x}(t)), \quad \bm{x}(0) = {\color{blue}\bm{\theta}}\)
事後分布を \( C(\bm{X}(\bm{\theta})) \)
ただし \( X = ( \bm{x}_1(\bm{\theta}) ,\dots, \bm{x}_N (\bm{\theta}))\)
Runge-Kutta法などによる近似解
\( \nabla_{\bm{\theta}}C(\bm{X}(\bm{\theta})) = \bm{0}\) となる \(\bm{\theta}\) を求めたい
- 誤差逆伝播法と同じ
- adjoint方程式 \(\displaystyle \frac{\mathrm d}{\mathrm dt}\bm{\lambda} (t) = - (\nabla_{\bm{x}}\bm{f}(\bm{x}(t)))^\top \bm{\lambda}(t)\) を，適切な終端条件のもと，
適切な離散化方法で時間逆向きに近似計算すればよい
Sanz-Serna 2016; Matsubara, Miyatake, Yaguchi 2021, 2023
勾配 \( \nabla_{\bm{\theta}}C(\bm{X}(\bm{\theta})) \) の計算 → 厳密に計算可能！
分散を計算したければ...
分散の計算
使用しているモデルに対して
近似解を使った場合
（原理的には計算可能）
事後分布をガウシアンで近似
（計算可能）
モデル：
\(\displaystyle \frac{\mathrm d}{\mathrm dt} \bm{x}(t) = \bm{f}(\bm{x}(t)), \quad \bm{x}(0) = {\color{blue}\bm{\theta}}\)
\( \mathsf{H}_{\bm{\theta}}C(\bm{X}(\bm{\theta}^\ast)) ^{-1}\) の計算
（ヘッセ行列の逆行列）
計算できること
- ヘッセ行列とベクトルの積： \( \mathsf{H}_{\bm{\theta}}C(\bm{X}(\bm{\theta}^\ast)) \bm{v}\)
- 2nd-order adjoint方程式を適切に離散化すればよい
- 厳密に計算できる（丸め誤差はあるが）
Ito, Matsuda, M. 2021
Adjoint-based exact Hessian computation
(\(-\log C\) を改めて \(C\))
\(\theta^*\)
行列ベクトル積が計算できれば，原理的には連立一次方程式が解ける！
さて，逆行列（の成分）をどう計算する？
連立一次方程式の解法の分類
直接法
反復法
ガウスの消去法，LU分解，コレスキー分解，...
定常反復法 （SOR法など）
Krylov部分空間法 （CG法など）
- 20世紀のトップ10アルゴリズム
- 原理的には \(n\) 反復以内で厳密解に到達
→ 逆行列を計算できる
条件数が小さくなるように行列（ヘッセ行列）を変換しよう！
悪条件？ 前処理！
標準的な前処理：
\( A \bm{x} = \bm{b} \)
\( \Leftrightarrow \)
\( (C^{-1}A C^{-\top}) \ C^\top \bm{x} = C^{-1}\bm{b} \)
\( \underbrace{(K^{-1}A K^{-\top})}_{\tilde{A}} \underbrace{\ K^\top \bm{x}}_{\tilde{\bm{x}}} = \underbrace{K^{-1}\bm{b}}_{\tilde{\bm{b}}} \)
(\( A = CC^\top \))
\( \Leftrightarrow \)
(\( A \approx KK^\top \))
コレスキー分解
\(\tilde{A}\) の条件数が小さくなるような \(K\) を 効率よく 見つける
ヘッセ行列は基本的に「悪条件」
- 収束が遅い
- 収束したように見えても，解を信頼できない
前処理を考える前提
ヘッセ行列
多くの連立一次方程式の特性
- 大規模
- 疎行列（行列ベクトル積は効率よく計算可能）
- 行列の全成分にアクセス可能
- 大規模
- 密行列（行列ベクトル積は効率よく計算可能）
- 行列の全成分の保持は困難
既存の前処理技法はほぼ使えない！
- 行列ベクトル積を \(n\) 回計算すれば行列の成分は分かる
- メモリの観点で保持は難しい
-
\(n\) 回も行列ベクトル積計算するよりも軽いコストで
連立一次方程式を解きたい
数値解析的 新課題
- 大規模
- 密行列（行列ベクトル積は効率よく計算可能）
- 行列の全成分の保持は困難
どのように前処理を行えばよい？
- このような特性の連立一次方程式全般に対して研究する
- データ同化 （逆問題） に着目して，モデルやアジョイント方程式の
段階で変数変換 （前処理） を行う
考えられるいくつかのアプローチ
どの程度まで条件数を小さくすべき？
最低限，分散の計算の不確実性は他の不確実性より小さくしたい
まとめ
すべてのきっかけは，2nd-order adjoint方程式の数値計算
- 「本当は何に困っているのか」を（数年かけて）議論すると
思いもよらぬ新しい課題がたくさんあった - 今日の２つのテーマ：今後も継続して研究する予定
- 南海トラフの断層すべりモニタリングのアップデートを目指している
- 核融合に関する研究者との連携も強化中
（現象の規模に対するデータの少なさなどが似ている）
松田さんとの研究
※ 複数の変数を同時に扱う場合は \( \mathrm{N} (0,\Sigma_n)\)
\( r_n^2 := (y_n - \widehat{x}_n)^2 \sim (\gamma^2 + \sigma_n^2)\chi_1^2\)
残差 \(=\) \((\) データ - 数値解 \()^2\) \(\sim\) \(\chi^2\)-分布 （自由度1）
- 誤差を「確率変数」でモデル化
\( \xi_n = \hat{x}_n - x(t_n) \sim \mathrm{N} (0,\sigma_n^2)\)
【気持ち】 \(\sigma_n\) が誤差のスケールを反映してほしい
観測ノイズがガウシアン \( y_n \sim \mathrm{N}(x(t_n),\gamma^2)\) ならば（かつ，簡単のため 観測オペレータ \(H=\mathrm{id.}\) ならば）
データと数値解を比べるモデル → \(\sigma_1^2,\dots,\sigma_N^2\) を推定
(Matsuda, M., SIAM/ASA UQ, 2021)
(Marumo, Matsuda, M., Appl. Math. Lett, 2023
この推定の際，何らかの事前知識を導入
単調回帰 （単調性の事前情報）
- 制約付き尤度最大化
\displaystyle \max_{\sigma_1^2,\dots,\sigma_N^2} \underbrace{\log p (r_1^2,\dots,r_N^2 \mid \sigma_1^2,\dots,\sigma_N^2)}
_{\displaystyle =\sum_{n=1}^N \log p(r_n^2\mid \sigma_n^2)} \quad \text{s.t.} \quad \sigma_1^2 \leq \cdots \leq \sigma_N^2
- 凸最適化（最適解は一意）
- 単調回帰理論（および手法）に帰着
- PAVA (pool adjacent violators algorithm) で高速に最適解が求まる
- 計算量：最悪でも \(\mathrm{O}(N^2)\)，通常は \(\mathrm{O}(N)\)
- 微分方程式の一回の時間発展計算に比べて無視できる
- ベイズ推定とも組み合わせ可能 (そろそろpreprint)
常微分方程式の初期値問題を陰的な数値解法で数値計算する場合
2009年頃（学部4年生）の個人的な疑問
誤差は時間発展に伴い（通常）増加する傾向
（実際の計算の誤差を知るのは困難だが...）
(非)線形ソルバの収束の閾値、
時間発展に伴って変更できると効率的？
しかし
当時は構造保存数値解法に強い関心
踏み込んで考察することはなかった
（閾値は十分小さくしないと構造保存性が失われる）
数値計算の不確実性定量化って何？
- 誤差を「定量的」に評価
さらに、「確率95%で誤差はこれくらい」というようなことがいえればベター
- 既存の「決定論的」な数値解法を確率統計（特にベイズ統計）の視点で理解
（精度保証とは似て非なる...イメージ）
様々なことに役立てたい
- 計算の効率化（無駄の削減）
- 逆問題に対してより適切な不確実性定量化
「これよりは良い！悪い！」というより、「だいたいこれくらい！」
UQ: Uncertainty Quantification
精度がすごく良いわけでもすごく悪いわけでもない計算が主なターゲット
なぜ、数値計算のUQが重要なのか？
「超高精度な計算は必要ないが，ラフ過ぎてもダメ」というシチュエーションは案外多い
例：PDEの計算，画像処理，逆問題，...
実際の計算の精度について，一定の信頼度を保って定量的評価ができれば有用
例えば逆問題の場合...
- 通常の理論で導いた95%信頼区間には，数値計算の影響は加味されていない
- 数値計算の誤差の定量化ができれば，バイアスの評価に繋がり，
より適切な信頼区間が構築できる
結局のところ数値解析との関係は？
（従来型の）数値解析
数値計算のUQ
計算前に定性的評価
計算後に定量的評価
関数解析など
確率・統計
いつ評価？
主要な道具
【私見】 数値解析の一トピックとみなしてもよい気がします
常微分方程式
今日、お話すること、しないこと
確率的手法
その他のトピック
- 数値線形代数（CG法など）
- 数値積分
- 連続最適化
- 偏微分方程式
Probabilistic Numerics
A free electronic version
for personal use only is available
昨年出版！
確率的でない（陽には用いない）手法
- ODEフィルタ・スムーザー
- 摂動解法
- データ活用手法（逆問題）
- parareal法を活用した手法
- ベイズ的再解釈
様々な動機で様々な手法が開発されていて
それぞれに利点と（大きな）欠点がある
計算の過程で確率を扱う
あとで比較したりはしますが，基本的に独立した内容です
特に微分方程式の数値計算に関連するUQの研究は...
計算のUQ研究の動向
- 数値解析学者はほぼ不在
- 欧米でも統計・データ同化・機械学習などで著名な研究者も参入しているが
コミュニティの広がりは限定的（結構仲良くしてくれる）
日本では...
- 「計算のUQ」と謳っている研究はほとんどないように思われる
- （実は融合的な研究がありうるのではと思っている）精度保証分野も強力
確率的手法
確率的でない（陽には用いない）手法
- ODEフィルタ・スムーザー
- 摂動解法
- データ活用手法（逆問題）
- ベイズ的再解釈
- parareal法を活用した手法
ODEフィルタ（とスムーザー）
（数式が煩雑になるのでアルゴリズムの詳細は示しません）
- 何らかの方法で，1ステップを計算（予測分布を出力）
- 何らかの方法で，予測分布を修正
基本的な考え方
どのように実現するか
- カルマンフィルタ（およびその拡張版）の理論・手法を応用
例えば，各時刻で修正された分布（フィルタ分布）の
平均：数値解
分散：誤差の定量化
とみなす
カルマンフィルタ
状態空間モデル
\bm{x}_{j} = F_j \bm{x}_{j-1} + \bm{\xi}_j
% y_{j+1} &= H v_{j+1} + \eta_{j+1}
\bm{y}_{j} = H _j\bm{x}_{j} + \bm{\eta}_{j}
一期先予測：
フィルタ：
（非線形モデルの場合に，線形化した行列を用いて予測・フィルタを行う手法を「拡張カルマンフィルタ」という）
\(p(\bm{x}_j\mid \bm{y}_{1:j-1})\)
\(p(\bm{x}_j\mid \bm{y}_{1:j})\)
\(\bm{x}_0 \sim \mathrm{N} (\bm{x}_{0\mid 0},V_{0\mid 0})\) : given に対して
\(\bm{x}_j \mid \bm{y}_{1:j} \sim \mathrm{N} (\bm{x}_{j\mid j},V_{j\mid j})\)
\(\bm{x}_j \mid \bm{y}_{1:j-1} \sim \mathrm{N} (\bm{x}_{j\mid j-1},V_{j\mid j-1})\)
を交互に計算
\(\bm{x}_{j\mid j-1} = F_j \bm{x}_{j-1\mid j-1}\)
\(V_{j\mid j-1} = F_j V_{j-1\mid j-1} F_j^\top + G_j Q_j G_j^\top\)
\( K_t = V_{j\mid j-1} H_j^\top (H_j V_{j\mid j-1} H_j^\top + R_j)^{-1}\)
\(\bm{x}_{j\mid j} = \bm{x}_{j\mid j-1}＋K_j (\bm{y}_j - H_j \bm{x}_{j\mid j-1})\)
\(V_{j\mid j} = V_{j\mid j-1}- K_j H_j V_{j\mid j-1}\)
システムモデル
観測モデル
\(\sim \mathrm N (\bm{0},Q_j)\)
\(\sim \mathrm N (\bm{0},R_j)\)
システムモデル
ODEに対する状態空間モデル
観測モデル
\mathbf{X}(t) : \begin{bmatrix}
\bm{x}(t) \\
\bm{x}^\prime(t)\\
\vdots\\
\bm{x}^{(\nu-1)}(t)
\end{bmatrix}
SDE: \( \mathrm d \mathbf{X}(t)=F\mathbf{X}(t) \mathrm dt +L \mathrm d \mathbf{\omega}_t\) を離散化して
\mathbf{x}_{j} = A(h) \mathbf{x}_{j-1} + \bm{\xi}_j
% y_{j+1} &= H v_{j+1} + \eta_{j+1}
F = \begin{bmatrix}
O & I & O & \cdots & O \\
O & O & I & O & \vdots \\
\vdots & & \ddots & \ddots & O \\
O & & & O & I \\
O & O & \cdots & O & O
\end{bmatrix}, \quad
L =
\begin{bmatrix}
\mathbf{0} \\
\mathbf{0} \\
\vdots \\
\mathbf{0}\\
\sigma \mathbf{1}
\end{bmatrix}
A(h) = \exp(hF), \quad
\bm{\xi}_j \sim \mathrm N (\mathbf{0},Q(h)),
% & Q(h) = \int_0^h \mathrm{e}^{Fs} LL^\top \mathrm{e}^{F^\top s} \,\mathrm ds
\mathbf{y}_{j} = E_1 \mathbf{x}_j - \bm{f}(E_0 \mathbf{x}_j) + \bm{\eta}_j
% y_{j+1} &= H v_{j+1} + \eta_{j+1}
E_0 = \begin{bmatrix}
I & O & O & \cdots
\end{bmatrix}, \quad
E_1 = \begin{bmatrix}
O & I & O & \cdots
\end{bmatrix}
観測は常に \(\mathbf{y}_j = \bm{0}\) であるとする
拡張カルマンフィルタにおける線形化の例
\( H = E_1\), \( H = E_1 - \nabla \bm{f} (E_0 \mathbf{x}_{j\mid j-1}) E_0\)
\( \displaystyle \frac{\mathrm d\bm{x}}{\mathrm dt} = \bm{f}(\bm{x}), \quad \bm{x}(0) = \bm{x}_0 \in \mathbb{R}^d\)
Q(h) = \int_0^h \mathrm{e}^{Fs} LL^\top \mathrm{e}^{F^\top s} \,\mathrm ds
相当の \(d\nu\) 次元ベクトル
\(\bm{x}^\prime \) 相当
\(\bm{x} \) 相当
ODEフィルタのポイント
- 高階微分相当もまとめた状態ベクトル
- 初期時刻における高階微分の計算は
「Taylorモード自動微分」
- 初期時刻における高階微分の計算は
- ベクトル場 \(\bm{f}\) の情報は使わなくてもよい
- かなり自由度がある
- 観測は常に \( \bm{0}\) ：
システムモデル
観測モデル
SDE: \( \mathrm d \mathbf{X}(t)=F\mathbf{X}(t) \mathrm dt +L \mathrm d \mathbf{\omega}_t\) を離散化して
\mathbf{x}_{j} = A(h) \mathbf{x}_{j-1} + \bm{\xi}_j
% y_{j+1} &= H v_{j+1} + \eta_{j+1}
A(h) = \exp(hF), \quad
\bm{\xi}_j \sim \mathrm N (\mathbf{0},Q(h)),
% & Q(h) = \int_0^h \mathrm{e}^{Fs} LL^\top \mathrm{e}^{F^\top s} \,\mathrm ds
\mathbf{y}_{j} = E_1 \mathbf{x}_j - \bm{f}(E_0 \mathbf{x}_j) + \bm{\eta}_j
% y_{j+1} &= H v_{j+1} + \eta_{j+1}
E_0 = \begin{bmatrix}
I & O & O & \cdots
\end{bmatrix}, \quad
E_1 = \begin{bmatrix}
O & I & O & \cdots
\end{bmatrix}
観測は常に \(\mathbf{y}_j = \bm{0}\) であるとする
Q(h) = \int_0^h \mathrm{e}^{Fs} LL^\top \mathrm{e}^{F^\top s} \,\mathrm ds
\(\bm{x}^\prime \) 相当
\(\bm{x} \) 相当
残差の計算により \(\bm{f}\) の情報を取り込む
FitzHugh—Nagumo model
数値実験（「驚異的」にうまく動作するわけではない）
\displaystyle
\begin{cases}
\frac{\mathrm dV}{\mathrm dt} =c \big(V - \frac{V^3}{3} + R \big) \\
\frac{\mathrm dR}{\mathrm dt} = -\frac{1}{c} \big( V-a+bR\big)
\end{cases}
EK1(\(\nu=1\))
EK1(\(\nu=2\))
EK1(\(\nu=3\))
- ProbNumDiffEq.jl
- 黒線：厳密解（reference solution）
- \(\mathrm{abstol}=10^{-2}, \mathrm{reltol}=10^{-1}\) として刻み幅制御を適用済
\(V\)
\(R\)
- EK0： \( H = E_1\),
- EK1： \( H = E_1 - \nabla \bm{f} (E_0 \mathbf{x}_{j\mid j-1}) E_0\)
- Python や Julia でパッケージ化はされているが，まだまだ実用レベルではない
- 近似解についての収束解析は議論されている
- 一方で，UQについての理論はほとんど無く，
「試してみて時々（パラメータによっては）うまく動作する」という域をでていない
感想？？
- 粒子フィルタとの組み合わせなどによる性能の向上は報告されている
- Nordsieck法（古典的解法の一種）との関連が指摘されている
確率的手法
確率的でない（陽には用いない）手法
- ODEフィルタ・スムーザー
- 摂動解法
- データ活用手法（逆問題）
- ベイズ的再解釈
- parareal法を活用した手法
決定論的解法 + 各時間ステップごとに摂動を加える (Conrad et al., 2016)
摂動解法
\( \displaystyle \frac{\mathrm dx}{\mathrm dt} = f(x), \quad x(0) = x_0 \in \mathbb{R}^d\)
決定論的解法の 刻み幅 をランダムに選ぶ (Abdulle, Garegnani, 2020)
\( \Psi_h:\mathbb{R}^d\to \mathbb{R}^d\): Runge–Kutta法などの通常の一段解法 として
\widehat{X}_n = \Psi_{h_n} ( \widehat{X}_{n-1}) + \xi_n (h_n), \quad \widehat{X}_0 = x_0
摂動
\widehat{X}_n = \Psi_{h_n} ( \widehat{X}_{n-1}) + \xi_n (h_n), \quad \widehat{X}_0 = x_0
\widehat{X}_n = \Psi_{H_n} ( \widehat{X}_{n-1}) , \quad \widehat{X}_0 = x_0
randomized step size
- 摂動を加えれば，\(\widehat{X}_n\) は確率変数
摂動の「心」
\widehat{X}_n = \Psi_{h_n} ( \widehat{X}_{n-1}) + \xi_n (h_n), \quad \widehat{X}_0 = x_0
- 局所誤差を確率変数でモデル化
各 \(t_n\) において分布が生成される
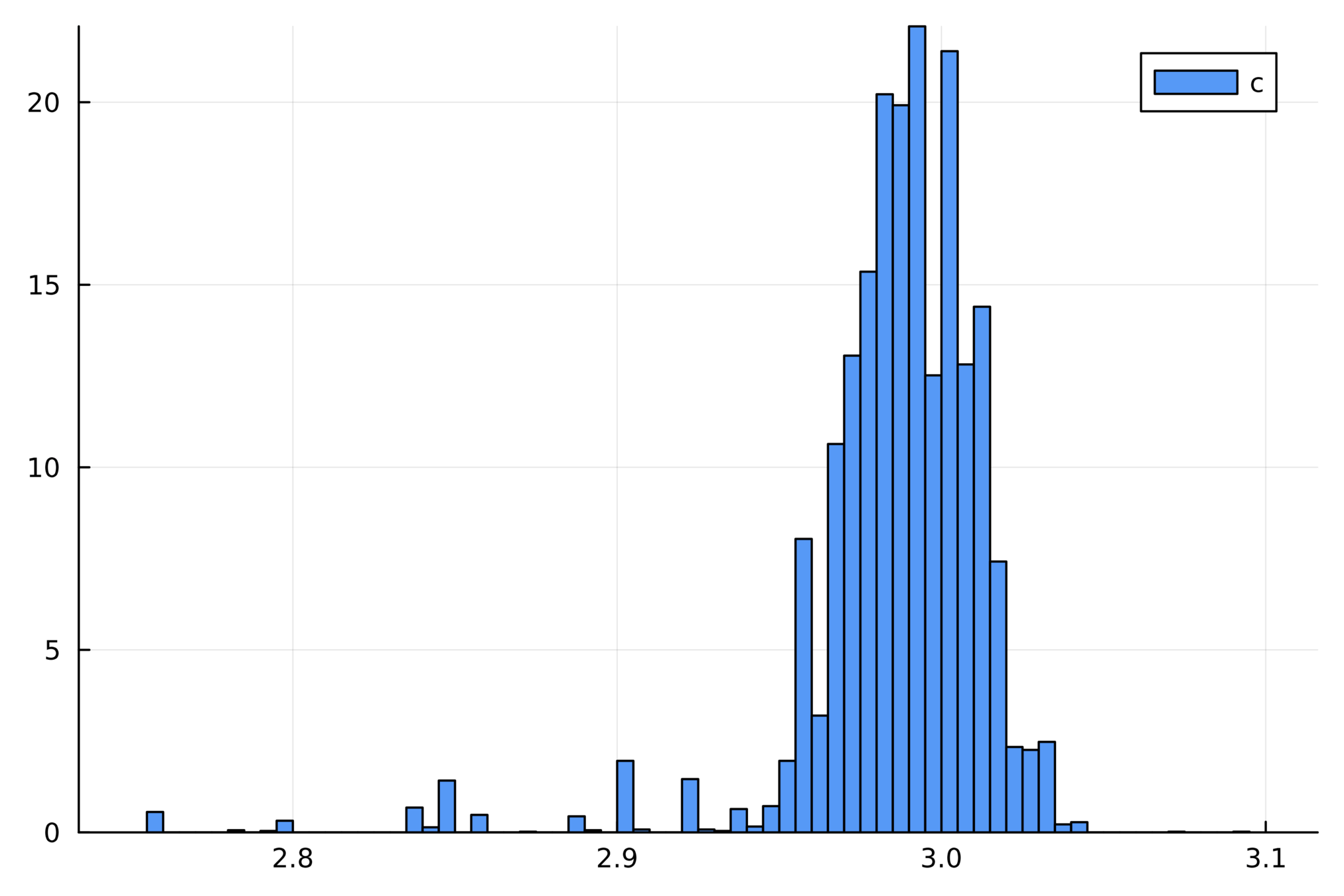
（実際の計算では複数のサンプルによるヒストグラム）
摂動解法の性質（収束解析）
\widehat{X}_n = \Psi_{h_n} ( \widehat{X}_{n-1}) + \xi_n (h_n), \quad \widehat{X}_0 = x_0
仮定
\displaystyle \mathbb{E} \bigg( \max_{n=0,\dots,N} \| \widehat{X}_n - x(t_n) \| \bigg) \leq C h^{\min(p,q)}
定理
(Lie, Stuart, Sullivan 2019; Conrad et al., 2017)
- \( \Psi_h\): \(q\) 次精度解法
- \( \exist C\), \( \displaystyle \mathbb{E} \big( \| \xi_n(t) \xi_n(t)^\top\|_{\text{F}}\big)\leq C t ^{2p+1}\)
- \( f\) についての様々な仮定
仮定
局所誤差 \(\approx \mathrm{O}(h^{q+1})\)
標準偏差 \(\approx \mathrm{O}(h^{p+1/2})\)
- \(p \geq q\): ランダムな出力は，決定論的ソルバより悪くはない
- \(p < q\): ランダムな出力の大域誤差の期待値は，決定論的ソルバより悪い
- Recommend: \(p=q\)
複数サンプルによるヒストグラム
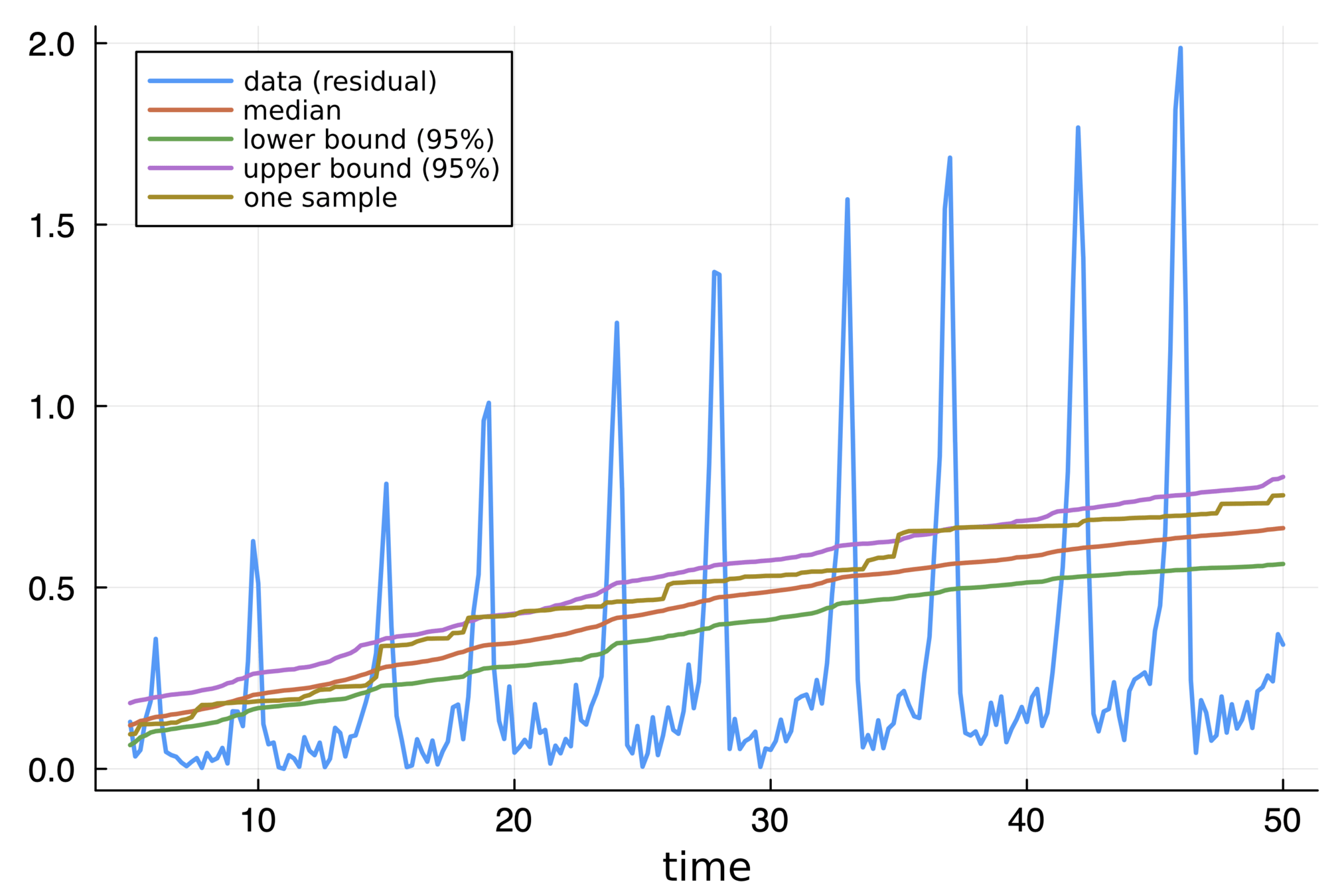
Lorenz system
\displaystyle
\begin{cases}
\frac{\mathrm dx}{\mathrm dt} = -px + py \\
\frac{\mathrm dy}{\mathrm dt} = -xz+rx-y \\
\frac{\mathrm dz}{\mathrm dt} = xy-bz
\end{cases}
- \(\Psi_h\): 通常のRunge–Kutta法
- \( \xi(h)\): 正規分布
- \(q=p=4\)
Lorenz system
- 各時刻で「ヒストグラム」の形状から
誤差の大きさや計算の信頼度を
定量化できそうな気分になる - ただし，絶対的な根拠があるわけではない
\(x\)
- 摂動によって，計算の誤差が小さくなることはない（これはたぶん仕方ない）
不満な点
- たくさんサンプルを取る必要があるため，計算コストは著しく増大
- 適切な摂動がよくわからない
- \(\Psi_h\) が構造保存解法の場合，摂動によって構造保存性が破壊される
たとえば，正規分布の場合，\(\mathrm{N}(\mathbb{0},\Sigma h^{2q+1})\) とするれば良さそうだが，
適切な \(\Sigma\) はどう選択するのか？
- これなら，\(\Psi_h\) が構造保存的な場合，ランダムな出力も構造保存的になる
- ただし，正値をとる分布が望ましい
刻み幅をランダムに！
\widehat{X}_n = \Psi_{H_n} ( \widehat{X}_{n-1}) , \quad \widehat{X}_0 = x_0
randomized step size
(Abdulle, Garegnani, 2020)
確率的手法
確率的でない（陽には用いない）手法
- ODEフィルタ・スムーザー
- 摂動解法
- データ活用手法（逆問題）
- ベイズ的再解釈
- parareal法を活用した手法
背景の（超簡略版）問題設定
逆問題：摂動の代わりにデータを使う
\displaystyle \frac{\mathrm d}{\mathrm dt} x(t) = f(x(t)), \quad x(0) = \theta
- モデル（微分方程式）：given (モデルの不確実性はないと仮定)
- 幾つかのシステムパラメータや初期値：unknown
\displaystyle y_1,\dots,y_N, \quad (y_n = Hx(t_n;\theta^*)+\varepsilon_n)
- ノイズ付き時系列観測データ：known (観測オペレータ\(H\)も既知)
最尤推定の定式化
\displaystyle \min_{\theta\in\Theta} \sum_{n=1}^N \| Hx(t_n;\theta)-y_n\|^2
\displaystyle \min_{\theta\in\Theta} \sum_{n=1}^N \| H\widehat{x}(t_n;\theta)-y_n\|^2
Ideal
Reality (use approx. sol.)
観測オペレータ
観測 at \(t=t_n\)
※観測オペレータの推定
Akita, M., Furihata, 2022
数値解を用いる影響
\displaystyle \min_{\theta\in\Theta} \sum_{n=1}^N \| Hx(t_n;\theta)-y_n\|^2
\displaystyle \min_{\theta\in\Theta} \sum_{n=1}^N \| H\widehat{x}(t_n;\theta)-y_n\|^2
Ideal
Reality (use approx. sol.)
\(\hat{\theta}_{\mathrm{ML}}\)
\(\hat{\theta}_{\mathrm{QML}}\)
バイアス： \( \mathrm{E}_{\theta} [\hat{\theta}_{\mathrm{QML}}] - \theta \neq 0\)
最小二乗誤差（mean squared error）： \( \mathrm{E}_{\theta} \big[\|\hat{\theta}_{\mathrm{ML}}-\theta\|^2\big] \) vs \( \mathrm{E}_{\theta} \big[\|\hat{\theta}_{\mathrm{QML}}-\theta\|^2\big] \)
MLE
Runge–Kutta
中点則
【考察】
数値計算の精度によって，
推定の性能は大きく異りうる
仮定：真のパラメータ \(\theta^*\) は既知
離散化誤差（各時刻の誤差）のモデル
実際には，例えば \(\theta\) の推定と（以下の）離散化誤差の定量化を交互に繰り返す
※ 複数の変数を同時に扱う場合は \( \mathrm{N} (0,\Sigma_n)\)
\( r_n^2 := (y_n - \widehat{x}_n)^2 \sim (\gamma^2 + \sigma_n^2)\chi_1^2\)
残差 \(=\) \((\) データ - 数値解 \()^2\) \(\sim\) \(\chi^2\)-分布 （自由度1）
(Matsuda, M., SIAM/ASA UQ, 2021)
観測 と 数値解 から「各時刻での誤差」を推定
以下の目的：
- 誤差を「確率変数」でモデル化
\( \xi_n = \hat{x}_n - x(t_n) \sim \mathrm{N} (0,\sigma_n^2)\)
【気持ち】 \(\sigma_n\) が誤差のスケールを反映してほしい
観測ノイズがガウシアン \( y_n \sim \mathrm{N}(x(t_n),\gamma^2)\) ならば（かつ，簡単のため 観測オペレータ \(H=\mathrm{id.}\) ならば）
データと数値解を比べるモデル → \(\sigma_1^2,\dots,\sigma_N^2\) を推定
観測データと数値解から \(\sigma_n^2\) を推定
- 制約付き尤度最大化
\displaystyle \max_{\sigma_1^2,\dots,\sigma_N^2} \underbrace{\log p (r_1^2,\dots,r_N^2 \mid \sigma_1^2,\dots,\sigma_N^2)}
_{\displaystyle =\sum_{n=1}^N \log p(r_n^2\mid \sigma_n^2)} \quad \text{s.t.} \quad \sigma_1^2 \leq \cdots \leq \sigma_N^2
- 凸最適化（最適解は一意）
- 単調回帰理論（および手法）に帰着
- PAVA (pool adjacent violators algorithm) で高速に最適解が求まる
- 計算量：最悪でも \(\mathrm{O}(N^2)\)，通常は \(\mathrm{O}(N)\)
- 微分方程式の一回の時間発展計算に比べて無視できる
FitzHugh–Nagumoモデル
数値実験
\displaystyle
\begin{cases}
\frac{\mathrm dV}{\mathrm dt} =c \big(V - \frac{V^3}{3} + R \big) \\
\frac{\mathrm dR}{\mathrm dt} = -\frac{1}{c} \big( V-a+bR\big)
\end{cases}
\(V\) の誤差について
- 誤差のだいだいの振る舞いは捉えているようにみえる
- 当然，「減る振る舞い」は捉えられない（捉えられる方が良いかどうかは問題依存）
正則化によって，単調制約を弱めることも可能
\displaystyle \min_{\sigma_1^2,\dots,\sigma_N^2} - \log p (r_1^2,\dots,r_N^2 \mid \sigma_1^2,\dots,\sigma_N^2) \quad \text{s.t.} \quad \sigma_1^2 \leq \cdots \leq \sigma_N^2
\displaystyle \min_{\sigma_1^2,\dots,\sigma_N^2} - \log p (r_1^2,\dots,r_N^2 \mid \sigma_1^2,\dots,\sigma_N^2) +\lambda \sum_{n=1}^N \max (\eta_i - \eta_{i+1},0)
\displaystyle \eta>0, \quad \eta_n := -\frac{1}{\gamma^2+\sigma_n^2}
正則化
(Matsuda, M., arXiv, 2021)
- 微分方程式の計算の不確実性定量化は今後重要な研究トピックになると思う
- 過去10年余り，様々なアイデアが提唱されているが，どれも決定打に欠ける
- 精度保証分野も含め，数値解析は大きく貢献できるはず！
まとめ
【私見】
【何が難しいのか】
- 時間発展に伴い誤差が 増減 する振る舞いを定量化しないといけない
→ さらに，誤差の定量化の信頼性をどのように議論すべきかは非自明 - 計算コストをかければ，それなりによい定量化手法は作れる
（そもそもあまり計算コストをかけたくないから，ほどほどの計算を行い，
その保証をつけたい，というのが動機の一つ）
mfip2024
By Yuto Miyatake
