Modeling Fraud in mobile money using Agent Based Simulations
“The key to artificial intelligence has always been the representation.” —Jeff Hawkins
Zachary D White Feb - 2019
Introduction to mobile money
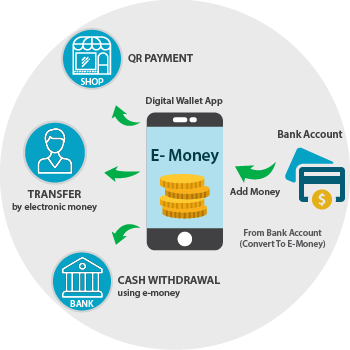
What is mobile Money?
mobile money market
in 2017

Mobile Money Fraud
Narrowing the Scope
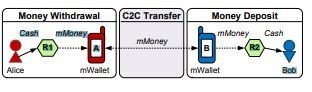
Fraud Scenarios
- Lost Accounts
- Scammed Customers
Multi-Agent based What?
Simulations
What's the system?
- Comprised of 3 Entities
- Clients
- Merchants
- Fraudsters

Why Do this?
- Lack of data
- Institutions don't share data on fraud
When Do WE see DATA?
df = pd.read_csv('PS_20174392719_1491204439457_log.csv')
df.head()
step type amount nameOrig oldbalanceOrg newbalanceOrig nameDest oldbalanceDest newbalanceDest isFraud isFlaggedFraud
0 1 PAYMENT 9839.64 C1231006815 170136.0 160296.36 M1979787155 0.0 0.0 0 0
1 1 PAYMENT 1864.28 C1666544295 21249.0 19384.72 M2044282225 0.0 0.0 0 0
2 1 TRANSFER 181.00 C1305486145 181.0 0.00 C553264065 0.0 0.0 1 0
3 1 CASH_OUT 181.00 C840083671 181.0 0.00 C38997010 21182.0 0.0 1 0
4 1 PAYMENT 11668.14 C2048537720 41554.0 29885.86 M1230701703 0.0 0.0 0 0DF.INFO()
Index
Binary
Label
Categorical
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 6362620 entries, 0 to 6362619
Data columns (total 11 columns):
step int64
type object
amount float64
nameOrig object
oldbalanceOrg float64
newbalanceOrig float64
nameDest object
oldbalanceDest float64
newbalanceDest float64
isFraud int64
isFlaggedFraud int64
dtypes: float64(5), int64(3), object(3)
memory usage: 534.0+ MBLargely Irrelevent
Closer Look
df['type'].value_counts(normalize=True)
CASH_OUT 0.351663
PAYMENT 0.338146
CASH_IN 0.219923
TRANSFER 0.083756
DEBIT 0.006512
Name: type, dtype: float64df[df['isFraud']==1]['type'].value_counts(normalize=True)
CASH_OUT 0.501157
TRANSFER 0.498843
Name: type, dtype: float64 Data transformation
# encode payment type
le = pp.LabelEncoder()
le.fit(df['type'])
df['type']=le.transform(df['type'])
>['CASH_IN', 'CASH_OUT', 'DEBIT', 'PAYMENT', 'TRANSFER']
>['0', '1', '2', '3', '4']
Model Set up TTS
X = df.drop(['isFraud','nameOrig','nameDest'],1)
Y = df['isFraud']
# T T S assign
X_train, X_test, y_train, y_test = train_test_split(X,Y, test_size=0.25,
stratify=Y, random_state=7351)
print('Train Set Class Balance\n',y_train.value_counts(normalize=True),
'\n\nTest Set Class Balance\n',y_test.value_counts(normalize=True))
Train Set Class Balance
0 0.997035
1 0.002965
Name: isFraud, dtype: float64
Test Set Class Balance
0 0.997036
1 0.002964
Name: isFraud, dtype: float64from scipy.stats import ttest_ind
ttest_ind(y_test,y_train)
Ttest_indResult(statistic=-0.006436921717865298, pvalue=0.9948641154723918)Turning the Knobs
params = {'loss': ['deviance','exponential'],
'learning_rate' : [0.1],
'n_estimators': [800],
'subsample': [.8],
'min_samples_split':[2],
'min_weight_fraction_leaf': [0,.1],
'max_depth': [2],
'tol':[0.00001],
'random_state':[7351]
}clf = ensemble.GradientBoostingClassifier()
skf = StratifiedKFold(n_splits=10)
grid = GridSearchCV(clf, params, cv=skf,scoring='recall',verbose=10)start_time = time.time()
#Fit the Data
grid.fit(X_train, y_train)
print("--- %s seconds ---" % (time.time() - start_time))
[Parallel(n_jobs=1)]: Done 40 out of 40 | elapsed: 1020.3min finished
--- 63018.65185260773 seconds ---params = {'loss': ['deviance','exponential'],
'learning_rate' : [ .01, 0.1],
'n_estimators': [800],
'subsample': [.8],
'min_samples_split':[2],
'min_weight_fraction_leaf': [0,.1],
'max_depth': [2],
'tol':[0.00001],
'random_state':[7351]
}
Fitting 10 folds for each of 8 candidates, totalling 80 fits
--- 102898.9753882885 seconds ---So we're done right?
Not even close
grid.best_score_
>0.7769118363370677
grid.best_params_
>{'learning_rate': 0.1,
'loss': 'exponential',
'max_depth': 2,
'min_samples_split': 2,
'min_weight_fraction_leaf': 0,
'n_estimators': 800,
'random_state': 7351,
'subsample': 0.8,
'tol': 1e-05}Test set accuracy:
Percent Type I errors: 4.212101304179725e-05
Percent Type II errors: 0.00028793170109168867
Accuracy by admission status
col_0 0 1 All
isFraud
0 1588535 67 1588602
1 458 1595 2053
All 1588993 1662 1590655
Percentage recall
77.69118363370677%False Negatives
False Positives
Why Recall?
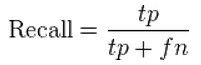
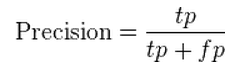
What do our results mean?
cost = pd.DataFrame()
cost['amount'] = X_test['amount']
cost['fraud'] = y_test.ravel()
cost['prediction'] = predict_test.ravel()#Dollars saved catching fraud
print('Dollars saved catching fraud\n','${:,.2f}'
.format(cost[(cost['fraud']==1) & (cost['prediction']==1)]['amount'].sum()))
#Cost of fraud not caught
print('\nDollars lost missing fraud\n','${:,.2f}'
.format(cost[(cost['fraud']==1) & (cost['prediction']==0)]['amount'].sum()))
#Difference
print('\nDifference between lost and saved\n','${:,.2f}'
.format(cost[(cost['fraud']==1) & (cost['prediction']==1)]['amount'].sum()
-
cost[(cost['fraud']==1) & (cost['prediction']==0)]['amount'].sum()))
# Total Transacted
print('\nTotal dollars transacted\n','${:,.2f}'.format(cost['amount'].sum()))Dollars saved catching fraud
$2,967,227,842.90
Dollars lost missing fraud
$100,041,133.17
Difference between lost and saved
$2,867,186,709.73
Total dollars transacted
$219,723,825,299.82Text
Test model on more data!
That's a lot of data!
<class 'pandas.core.frame.DataFrame'>
Int64Index: 19895884 entries, 0 to 3432364
Data columns (total 12 columns):
step int64
action object
amount float64
nameOrig object
oldBalanceOrig float64
newBalanceOrig float64
nameDest object
oldBalanceDest float64
newBalanceDest float64
isFraud int64
isFlaggedFraud int64
isUnauthorizedOverdraft int64
dtypes: float64(5), int64(4), object(3)
memory usage: 1.9+ GBAccuracy by admission status
col_0 0 1 All
isFraud
0 19887444 54 19887498
1 3763 4623 8386
All 19891207 4677 19895884
Percentage accuracy
0.9998081512739017
Percentage Fraud caught
0.5512759360839494# Load in new data from subsequent simulations
df1 = pd.read_csv('Run1.csv')
df2 = pd.read_csv('Run2.csv')
df3 = pd.read_csv('Run3.csv')
df4 = pd.read_csv('Run4.csv')
df5 = pd.read_csv('Run5.csv')
dftest=pd.concat([df1,df2,df3,df3,df4,df5])A = [df1,df2,df3,df4,df5]
for i in A:
print(split_pred(i,clfb))
DF1 Percent True Negatives Predicted
0.5522598870056498
DF2 Percent True Negatives Predicted
0.5450704225352113
DF3 Percent True Negatives Predicted
0.5547337278106509
DF4 Percent True Negatives Predicted
0.5545454545454546
DF5 Percent True Negatives Predicted
0.5466101694915254Train a new model
def split_search_pred(df):
# must change this to check if data is already in correct format.
# change / reshape data
df.drop(['isFlaggedFraud','isUnauthorizedOverdraft'],1,inplace=True)
df.rename(columns={'action':'type','oldBalanceOrig':'oldbalanceOrg','newBalanceOrig':'newbalanceOrig','oldBalanceDest':'oldbalanceDest','newBalanceDest':'newbalanceDest'},inplace=True)
#encode type
le.fit(df['type'])
df['type']=le.transform(df['type'])
#split into dependant and independant variable(s)
# T T S assign
X = df.drop(['isFraud','nameOrig','nameDest'],1)
Y = df['isFraud']
X_train, X_test, y_train, y_test = train_test_split(X,Y, test_size=0.25, stratify=Y, random_state=7351)
params = {'loss': ['deviance','exponential'],
'learning_rate' : [ .01, 0.1],
'n_estimators': [800],
'subsample': [.8],
'min_samples_split':[2],
'min_weight_fraction_leaf': [0,.1],
'max_depth': [2],
'tol':[0.00001],
'random_state':[7351]
}
xgb_model = xgb.XGBClassifier()
skf = StratifiedKFold(n_splits=10)
xgb_grid = GridSearchCV(xgb_model, params, cv=skf,scoring='recall',verbose=10)
start_time = time.time()
#Fit the Data
xgb_grid.fit(X_train, y_train)
print("--- %s seconds ---" % (time.time() - start_time))
return gridTest and evaluate
df1 = pd.read_csv('Run2.csv')
cost_df1 = model_data(df1,xgb_grid_opt)
def model_data(df,model):
# must change this to check if data is already in correct format.
# change / reshape data
df=df
df.drop(['isFlaggedFraud','isUnauthorizedOverdraft'],1,inplace=True)
df.rename(columns={'action':'type','oldBalanceOrig':'oldbalanceOrg','newBalanceOrig':'newbalanceOrig','oldBalanceDest':'oldbalanceDest','newBalanceDest':'newbalanceDest'},inplace=True)
#encode type
le = pp.LabelEncoder()
le.fit(df['type'])
df['type']=le.transform(df['type'])
#split into dependant and independant variable(s)
X = df.drop(['isFraud','nameOrig','nameDest'],1)
Y = df['isFraud']
print('Starting prediction')
#use model to predit
cost = model_evaluate(model,X,Y)
cost['nameOrig'] = df['nameOrig']
cost['nameDest'] = df['nameDest']
return costTest set accuracy:
Percent Type I errors: 0.0002624220326785749
Percent Type II errors: 1.8851297672463193e-05
Accuracy by admission status
col_0 0 1 All
isFraud
0 3339648 877 3340525
1 63 1357 1420
All 3339711 2234 3341945
Evaluation Contd
What do our results mean
Test set accuracy:
Percent Type I errors: 0.0002624220326785749
Percent Type II errors: 1.8851297672463193e-05
Accuracy by admission status
col_0 0 1 All
isFraud
0 3339648 877 3340525
1 63 1357 1420
All 3339711 2234 3341945
Type 1 and Type 2 Error represents waste
Represents the justification for keeping your job
Projected fraud department "case-load"
What do we do now?
cost_df1['isRefund'] = 0 #comment this out later, just to reset the refund column inbetween runs
cheat = cost_df1[((cost_df1['type']==1) | (cost_df1['type']==4)) & (cost_df1['fraud']==1)]
cheat.reset_index(inplace=True)
cheat.head(12)
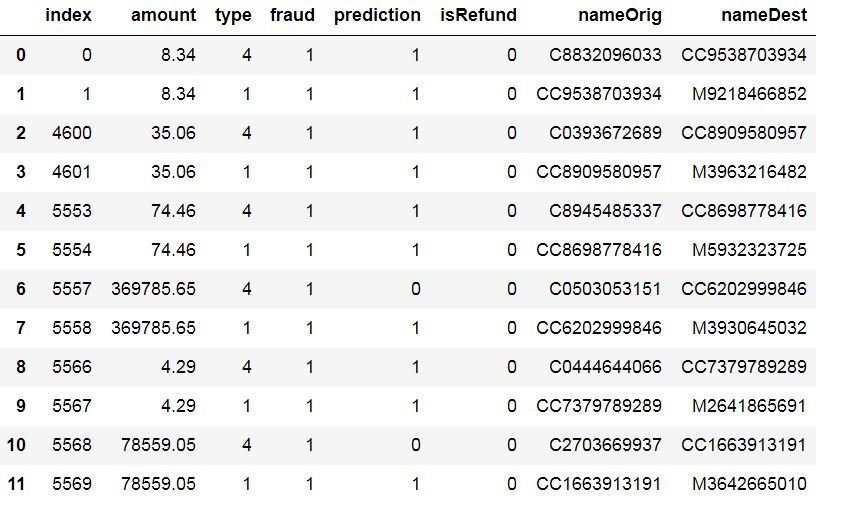
cALCULATING THE rEFUND
def adj_confmat(df):
for i in range(len(df.index)):
if i+1==(len(df.index)):
break
row = df.iloc[i,:]
# look for transfer transactions correctly predicted as fraud
if (row['type']==4) and (row['fraud']==1) and (row['prediction']==1):
# flag the transfer as being refunded
df.at[i,'isRefund']=1
#look at subsequent cash_out if it was "not caught" assume that it was because the transfer was caught
#ensure that the amounts are the same "not a realistic assumption insitu"
if (df.iloc[i+1,:]['type']==1) and (df.iloc[i+1,:]['fraud']==1) and (df.iloc[i+1,:]['prediction']==0) and (row['amount']==df.iloc[i+1,:]['amount']):
df.iat[i+1,'prediction']==1
# look for Cash_outs that were predicted, but the previous transfer was not caught
if (row['type']==1) and (row['fraud']==1) and (row['prediction']==1):
#look at previous transfer and set prediction to 1 as the
if (df.iloc[i-1,:]['type']==4) and (df.iloc[i-1,:]['fraud']==1) and (df.iloc[i-1,:]['prediction']==0) and (row['amount']==df.iloc[i-1,:]['amount']):
df.at[i-1,'prediction']=1
#print(df.iloc[i-1,:])
df.at[i,'isRefund']=1
#print("we found 1")
return df
test = adj_cheat(cheat)
Accuracy by admission status
col_0 0 1 All
isFraud
0 3339648 877 3340525
1 18 1402 1420
All 3339666 2279 3341945
test[test['isRefund']==1]['amount'].sum()
Dollars Refunded to Customers
2,851,462,501.44$
Percentage of Fraud Caught
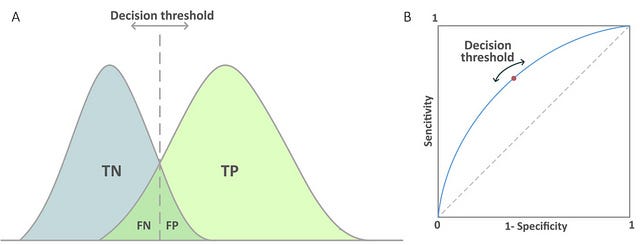
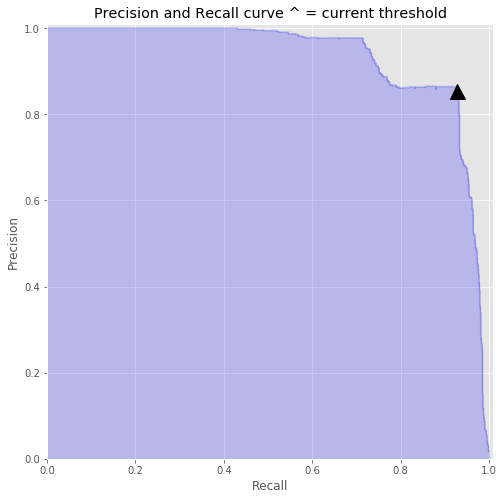
98.73%Decision Threshold
ARE WE DONE NOW? Is the answer ever yes?
df1_adj_eval = adj_conf(df1_fraud)
Accuracy by admission status
col_0 0 1 All
isFraud
0 3339648 877 3340525
1 18 1402 1420
All 3339666 2279 3341945
df1_adj_eval[df1_adj_eval['isRefund']==1]['amount'].sum()
Dollars Refunded to Customers
2,851,462,501.44$
Percentage of Fraud Caught
98.73%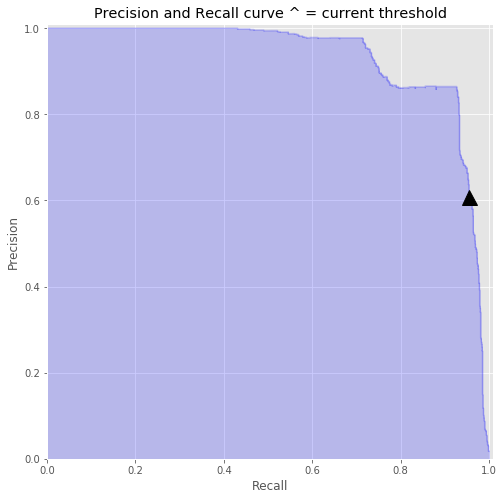
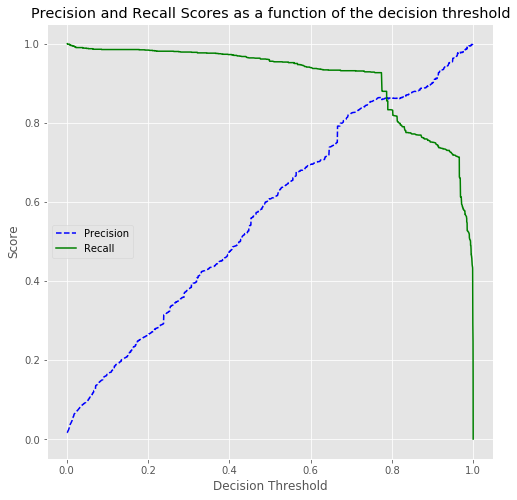
pred_pos pred_neg
pos 3340300 225
neg 102 1318
Adjusted for refunded transactions
Accuracy by admission status
col_0 0 1 All
isFraud
0 3340300 225 3340525
1 24 1396 1420
All 3340324 1621 3341945
# Dollars Refunded
$2,849,545,091.61
#Cost Difference between
#Decision Thresh = .75 and .5
$1,917,409.83
# Predicted Case Load difference
~ 610 Fewer casesDecision Threshold
With Refund
Final words
Lessons learned
pip install joblib
from joblib import dump, load
xgb_grid_opt = load('grid_opt_df1')# T T S assign
X_train, X_test, y_train, y_test = train_test_split(X,Y, test_size=0.25, stratify=Y, random_state=7351)
....
skf = StratifiedKFold(n_splits=10)
grid = GridSearchCV(clf, params, cv=skf,scoring='recall',verbose=10)Future work / Sources
- Applying Simulation to the Problem of Detecting Financial Fraud
- No Smurfs: Revealing Fraud Chains in Mobile Money Transfers
- FraudMiner: A Novel Credit Card Fraud Detection Model Based on Frequent Itemset Mining
- Fraud Detection within Mobile Money
- The Pay Simulator Github
- Fine tuning a classifier in scikit-learn
Thank you! :)
How does it work?

This is a stock image to look at while I talk at you.
Simulated Fraud Presentation
By Zak White
Simulated Fraud Presentation
Categorizing Fraud in Mobile Money Multi-Agent Based Simulations
- 163

