競技プログラミング練習会
2019 Normal
担当:zeke
第17回:ゲーム理論とか
自己紹介
zeke
京都大学工学部工業化学科B1
AtCoder:緑(1043)
競プロではC++を使っています
みんげーとかWebserviceとか
最近、自転車を買いました
今年からの初心者なのでお手柔らかにお願いします
今日の内容
今日の内容
ゲーム
競プロにおけるゲームとは?
- 基本二人
- 両者が「最善を尽くす」
- その結果を求める
- 所謂「ナッシュ均衡」(なんも知らんけど…)
- AtCoderによく出てくるイメージ
解き方のアプローチがいっぱい!!!
ゲーム問題の基本構想
ゲームのグラフ
- ゲームの状態遷移をグラフに対応させてみる
- ゲームグラフには二種類あって「引き分け」が存在しないかするかで分ける
- 前者はDAG(合流あり、サイクルなし)となり、具体例としてはオセロ、五目並べ
- 後者はサイクル、つまり、無限ループが起こる、具体的には将棋(千日手でループ回避)などがある
- 競プロでは、とりあえず前者が多い
五目並べのDAG
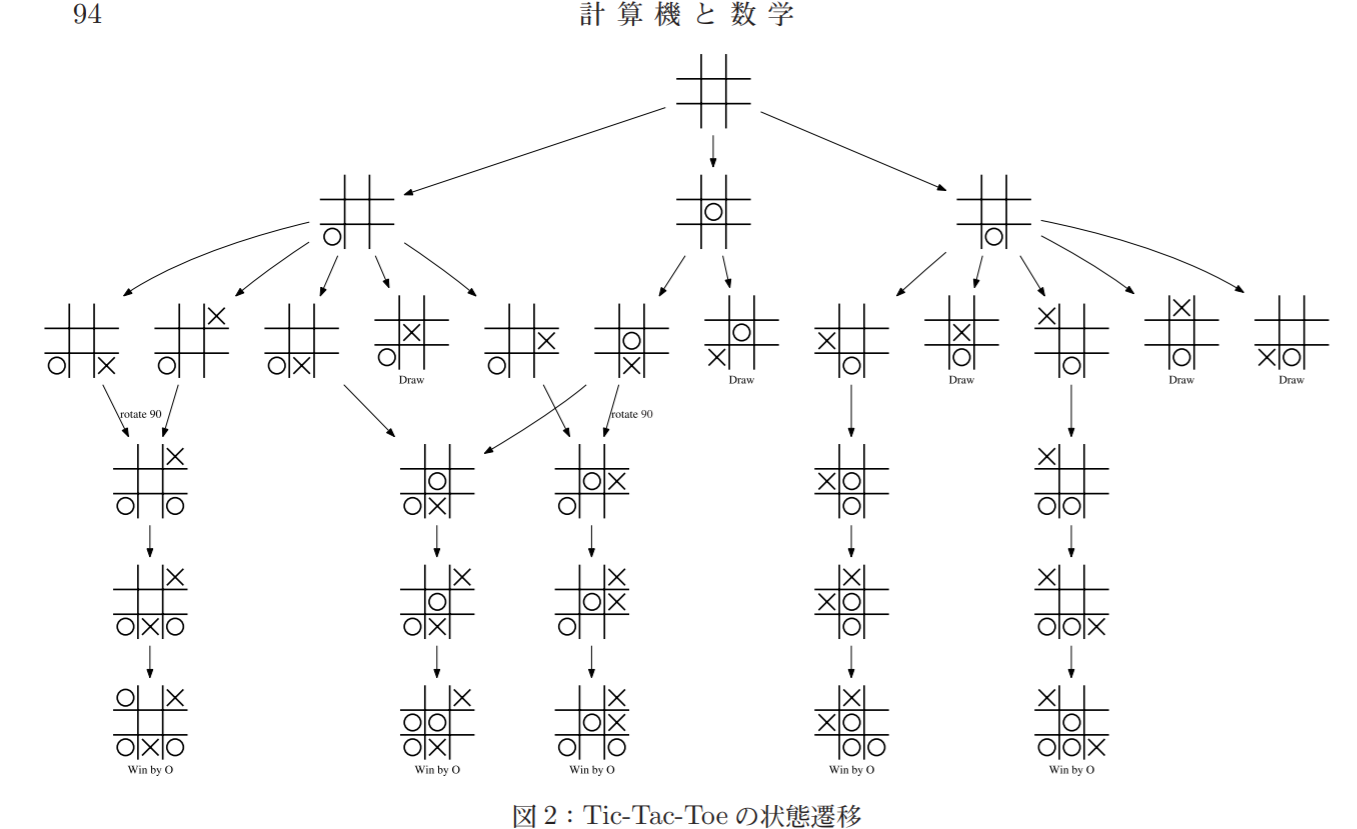
有向グラフであることが分かります
DAGグラフについて
- 解き方として、まず思いつきそうなのがDP,メモ化再帰などで各状態の勝ち負け状態をメモすること
- 状態数が1e7程度であれば計算可能(脳死DP)
- しかし、法則性に気づけば瞬殺で終わることもある (例:偶奇で場合分けなど)
- 後ほど詳しく説明します
それでは、このようなグラフは?
つまりは
- 一回、緑の状態になると、そこからは脱出できない
- いわゆる「引き分け」状態
- 後で説明する「後退解析」を用いて解く
Grundy数
Grundy数の話をする前に
- 有名な石取りゲームを考えてみる
石取りゲーム
- 二人のプレイヤーが、与えられた石の山から1~3個の石を取り合う
- 石が取れなくなったら負け
- 両者とも最善手を取り続けた場合、先手後手どちらが有利?
- 有名な問題で、必勝法がある
- これをGrundy数を用いて考えてみる
Grundy数とは
”ゲームの局面に対して割り当てられる、0 以上の整数”
Grundy数が0の状態を保持したとき必敗である
石取りゲームで考えてみる
| 残された石 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|---|
| Grundy数 |
石取りゲームで考えてみる
| 残された石 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|---|
| Grundy数 | 0 |
残された石0の時は自明
石取りゲームで考えてみる
| 残された石 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|---|
| Grundy数 | 0 | 1 |
残された石0の時は自明
遷移可能な状態で0以上の最小の整数
石取りゲームで考えてみる
| 残された石 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|---|
| Grundy数 | 0 | 1 | 2 |
残された石0の時は自明
遷移可能な状態で0以上の最小の整数
石取りゲームで考えてみる
| 残された石 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|---|
| Grundy数 | 0 | 1 | 2 | 3 |
残された石0の時は自明
遷移可能な状態で0以上の最小の整数
石取りゲームで考えてみる
| 残された石 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|---|
| Grundy数 | 0 | 1 | 2 | 3 | 0 |
残された石0の時は自明
遷移可能な状態で0以上の最小の整数
遷移先が1,2,3しかないのに注意
石取りゲームで考えてみる
| 残された石 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|---|
| Grundy数 | 0 | 1 | 2 | 3 | 0 | 1 |
残された石0の時は自明
遷移可能な状態で0以上の最小の整数
石取りゲームで考えてみる
| 残された石 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|---|
| Grundy数 | 0 | 1 | 2 | 3 | 0 | 1 | 2 |
残された石0の時は自明
遷移可能な状態で0以上の最小の整数
石取りゲームで考えてみる
| 残された石 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|---|
| Grundy数 | 0 | 1 | 2 | 3 | 0 | 1 | 2 | 3 |
残された石0の時は自明
遷移可能な状態で0以上の最小の整数
石取りゲームで考えてみる
| 残された石 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|---|
| Grundy数 | 0 | 1 | 2 | 3 | 0 | 1 | 2 | 3 | 0 |
残された石0の時は自明
遷移可能な状態で0以上の最小の整数
石取りゲームで考えてみる
| 残された石 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|---|
| Grundy数 | 0 | 1 | 2 | 3 | 0 | 1 | 2 | 3 | 0 |
残された石0の時は自明
遷移可能な状態で0以上の最小の整数
結論:石の数4の倍数で後手必勝
他は先手必勝
とりあえず
Grundy数が0になる状態を相手に渡せばいい
- Grundyが0以外の時0にすることができる
- Grundyが0の時どう頑張っても相手には0を渡せない
- 帰納的にGrundyが0になる人が負ける
- 考え方としてはゴールから逆算するイメージ?
- 先ほど説明したDAGの各頂点に数字を振り分けた感じ
- 無意識のうちにやっていることが多い(偶奇で処理とか)
- でも意識してやると、なんとなくコードを書いてWAを生やしてしまうのを防げるかも?
- 実際に配列としてGrundy数を格納する場合はセグメント木を使うと高速化できそう
Nim
こんな問題があるらしいです
- n個のコインの山がある。二人のプレイヤーは以下の操作を行う。プレーヤーは自分の番の時1つの山を選んで、その山から1枚以上のコインを取り除く。これを2人で交互に行い、取り除くコインがなかったらその時点で負けになる。両者が最善を尽くしたとき先手、後手どちらが勝つか。
結論
全ての山のXOR和をとる
0の時後手、それ以外だと先手必勝
簡単な証明
- 負け確状態はすべての山は0、つまりXOR和も0
- XOR和が0の時、何らかの操作をすることで0以外になってしまう(勝ち状態に絶対遷移)
- XOR和が0以外の時、適切な操作で0にすることが絶対できる(負け状態に遷移可能)※詳細な証明省く
- このように勝ち負け状態をXOR和として表現する手法
XORのTips
- nを偶数としたとき、n^(n+1)は1
- この性質を使うことで高速にXOR和を求めることが可能
- A=A^A^A=A^A^A^A^A…
関連問題
ゲームDP(easy)
ゲームDP
- DPの一つ
- 先ほど説明したGrundy数と似ていて勝ち負け状態を遷移させることが多いらしい(勝ち負け状態をboolで保持)
- もちろん、数としてメモすることもある
- どちらにせよ、ゲームのある状態をメモするのは同じ
- メモ化再帰とか区間DPとか、やり方たくさん
N 個の正整数 a1,a2,…,aNが与えられます。
K 個の石が山になっていて、先手と後手が交互に
山から a1,a2,…,aN のいずれかの個数の石をとる
を繰り返します。ただし、山に残っている石の個数より多くの個数の石をとることはできません。先に山から石がとれなくなった方の負け (最後の石をとった方が勝ち) です。先手と後手がお互いに最善を尽くしたとき、勝つのはどちらでしょう?
考察
- 状態(あと何個石が残っているかで)勝ち負け状態を定義することが可能
- dp[i]:石が残りi個で勝ちかどうかをboolで保持
- dp[0]はfalse(確実に負け)
考察(続き)
- 確実に負けに遷移するのが勝ちの状態
- 後ろから見たら終わり
- 計算量はO(NK)
コード例
int main(){
//入力からのdpテーブル準備
//初期化dp[0]=0;
//どうでもいいですが、0index,1indexどっちがいいんだろ
rep3(i,1,k+1){
bool h=false;
rep(j,n){
int k=i-vec[j];
//一個でも負けパターンあったら、その状態は勝確
if(k>=0&&dp[k]==0)h=true;
}
//勝フラグを立てる
if(h)dp[i]=1;
}
if(dp[k])cout<<"First"<<endl;
else cout<<"Second"<<endl;
}後退解析
後退解析
- さっきのDPだと「引き分け」は存在しない
- 今回は無限ループ(問題中だと1e9手目とか)を処理していく
- さっき示したグラフを思い出してほしい
考察、実装
- まず「引き分け」状態はどのようなものか
- 「負け」に遷移できない
- 遷移先に状態が不確定な頂点が存在する
- つまり、勝ち確実、負け確実な頂点を全探索して残ったやつが引き分けな頂点!
考察、実装
- まず勝ち確、負け確の頂点を全部queueにつっこむ
- ここからwhile文でqueueの中身がなくなるまで、頂点探索を続ける
- まず、確定頂点に伸びている辺を見てみる
- もしすでに確定していたら飛ばす
- 負け確定頂点にいく辺だったら、その頂点は文句なしで勝ち頂点
- 勝ち確定頂点にいく辺で、その不確定な頂点から出ている辺が勝ち確定頂点にいく辺のみだったら、その頂点は負け頂点
- 他は、今のところ分からないので保留
Q をキューとする
dp テーブル全体を -1 に初期化する
for each 各ノード v do
if deg[v] == 0 then
dp[v] = 0
v を Q に push
while Q が空ではない do
Q からノード v を pop して取り出す
for each v を終点とする辺 e とその始点のノード nv do
if nv はすでに訪れたノード then
continue
辺 e をグラフから削除 (実装上は deg[nv] の値を減らせば OK)
if dp[v] = 0 then
dp[nv] = 1
nv を Q に push
else if dp[v] = 1 then
if deg[nv] = 0 then (辺を削除して行ったことで出次数が 0 になったら負けノード確定です)
dp[nv] = 0
nv を Q に pushQ をキューとする
dp テーブル全体を -1 に初期化する
for each 各ノード v do
if deg[v] == 0 then
dp[v] = 0
v を Q に push
while Q が空ではない do
Q からノード v を pop して取り出す
for each v を終点とする辺 e とその始点のノード nv do
if nv はすでに訪れたノード then
continue
辺 e をグラフから削除 (実装上は deg[nv] の値を減らせば OK)
if dp[v] = 0 then
dp[nv] = 1
nv を Q に push
else if dp[v] = 1 then
if deg[nv] = 0 then (辺を削除して行ったことで出次数が 0 になったら負けノード確定です)
dp[nv] = 0
nv を Q に push後退解析の例(drkenさんのサイトから)
負け確の頂点を決めるとき、出自数を事前にメモっておくと、決めやすくなります
その他のゲーム問題
バリエーション豊か
- 実験しまくる
- 相手の行動をパクると勝つ
- じつはゲームではなかった
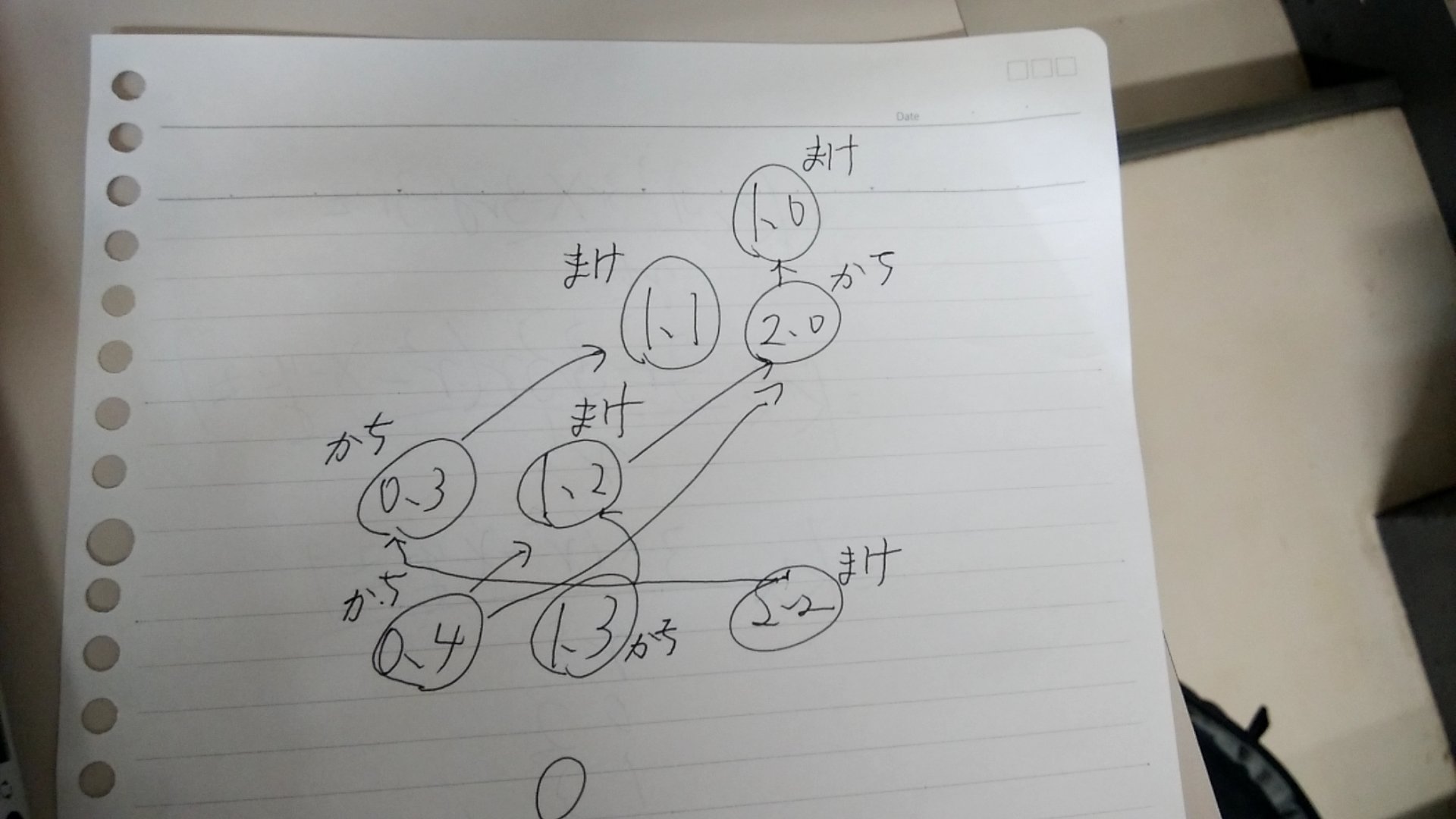
実験について
- とりあえず、負確状態を考える
- そこからグラフを作る(手書きする)
- 勝(負け)状態の共通点を探す
- それを帰納的に示す
- イメージとしては高校数学の「答えを~と仮定して数学的帰納法として示す~」のパターン
例
コンテスト
コンテスト
個人的にVjudgeが嫌いなので、素敵なUIの
AtCoder Virtual Contest
を使います!!!!!!!!!
誠に申し訳ありませんが、アカウント持っていない人は
ささっと作ってください
何と、自分の名前の色を自由に変えられます!
コンテストページ
お世話になったサイト
参考資料
解説とか(コンテスト後)
解説
自分用に解説作りました
よければ見ていてください
カードと兄弟
頑張る
石取り大作戦
- 石取りゲームだけど、両者平等じゃない
- 多く取れるほうが圧倒的に有利そう
- →A,Bの大小で場合分け
- A=Bのとき、Grundy考えて、Nが(A+1)の倍数で後手、他、先手必勝
- A>Bのとき、後手がどうあがいても勝ち目なし
- A<Bのとき、最初にAが取りきる以外にAに勝ち目なし
コード例
int main() {
cin.tie(0);
ios::sync_with_stdio(false);
ll n,a,b;
cin>>n>>a>>b;
if(a>b){
cout<<"Takahashi"<<endl;
}else if(a==b){
if(n%(a+1)==0){
cout<<"Aoki"<<endl;
}else{
cout<<"Takahashi"<<endl;
}
}else{
if(n<=a){
cout<<"Takahashi"<<endl;
}else{
cout<<"Aoki"<<endl;
}
}
}Alice&Brown
- 実験をしてみる(実はさっきの写真の奴がこれ)
- やってると、どうも2つの山の差が小さいときに先手が負ける
- 差が1以下の時後手必勝なんじゃないかと気づく
- 適当に証明する
- 実装はA問題レベル
コード例
int main() {
cin.tie(0);
ios::sync_with_stdio(false);
ll x,y;
cin>>x>>y;
if(abs(x-y)<=1){
cout<<"Brown"<<endl;
}else{
cout<<"Alice"<<endl;
}
}O(1)
Two Piles
- 実験する
- (0,0)負け
- (0,1)は勝
- というか山一つだと勝ち
- つまり山は二つのまま
- にしておきたい
- (1,1)は負け
- (X,1)の時X減らすと負ける
- じゃん!
- 1個ずつ減らす
- (X,1)X=even 勝 X=odd 負
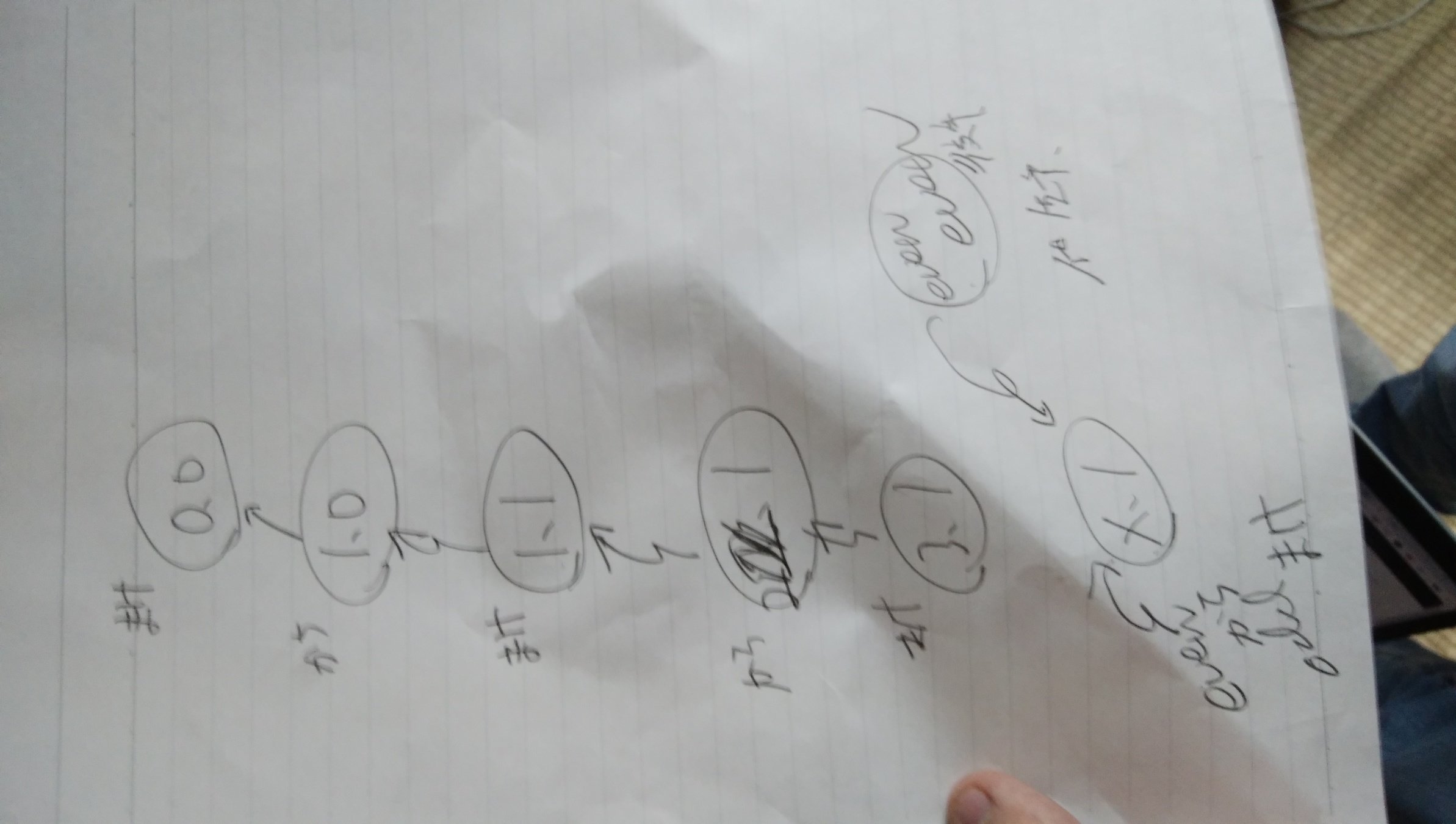
続き
- 先手は最初に(X,1) X=oddにしたい
- 両方とも偶数の時以外の時できそう
- 結論,両方偶数で後手、他先手必勝
コード例
int main(){
int a,b;
cin>>a>>b;
if(a%2==0||b%2==0)cout<<"Yes"<<endl;
else cout<<"No"<<endl;
}茶碗と豆
- 難しい
- GrundyとNimの合わせ技
- まず各茶碗に対して、Grundy数を求める
- 各豆に対してXOR和を求める
- 0の時後手必勝、他先手必勝
茶碗と豆(プラスアルファ)
- これでも満点回答ではない
- 先ほど説明したXORのTipsを使ってさらに高速化
- これでも満点回答ではない(マジか)
- Grundy数をもっと高速に求める
- 区間の最小値…→segtree!
- ここら辺は、よくわからないので強い人頑張ってください
ゲーム
- 来ましたゲームDP、TDPCの問題です
- すぬけ君とすめけ君が出てきます
- 先手目線で考えるといいかも
- dp[i][j] 左にi右にj残っているときに先手が最善尽くしたときの価値の合計
- 先手は最善手を後手は最悪手を放つと考えよう
ゲーム(続き)
- 片方の山がないとき
- 後手がさすとき,そのまま先手の点数に変動なし
- 先手がさすとき、その時の得点を足す
- 両方の山が存在するとき
- 後手dp[i][j]=min(dp[i-1][j],dp[i][j-1])
- 先手dp[i][j]=max(dp[i-1][j]+A[a+1-i],dp[i][j-1]+B[b+1-j])
- 初期化dp[i][j]=0
コード例
int main(){
int a,b;
cin >> a >> b;
vector<int> A(a+5);
vector<int> B(b+5);
//逆からやるのに留意
for(int i=0;i<a;i++){
int x;
cin >> x;
A[i+1]=x;
}
for(int i=0;i<b;i++){
int x;
cin >> x;
B[i+1]=x;
}
vector<vector<int>> dp(a+5,vector<int>(b+5));
//dp[i][j] 左にi右にj残っているときに先手が最善尽くしたときの価値の合計
//つまり先手は最善の手を、後攻は最悪手を放つように見える
for(int i=0;i<a+1;i++){
for(int j=0;j<b+1;j++){
int judge=(a+b-i-j)%2;
//先手か後手か?
if(i==0 && j==0){
dp[i][j]=0;
//なんもないときは当然0
//山がどちらかないとき
}else if(i==0){
if(judge==1){
dp[i][j]=dp[i][j-1];
//後手がとっても先手の合計は増えないことに注意
}else{
dp[i][j]=dp[i][j-1]+B[b+1-j];
}
}else if(j==0){
if(judge==1){
dp[i][j]=dp[i-1][j];
}else{
dp[i][j]=dp[i-1][j]+A[a+1-i];
}
}else{
if(judge==1){
dp[i][j]=min(dp[i-1][j],dp[i][j-1]);
//もちろんその場での最悪手をとる
}else{
dp[i][j]=max(dp[i-1][j]+A[a+1-i],dp[i][j-1]+B[b+1-j]);
//最善手
}
}
}
}
cout<<dp[a][b]<<endl;
}マス目と駒
- はいDP
- 二次元配列でやるのがよさそう
- 始めに、もういけないところ(負け確定マス)に印をつける
- 下から順番に、負けマスに行けるマスを勝ち、他を負けマスとメモする
コード例
int main() {
cin.tie(0);
ios::sync_with_stdio(false);
int h,w;
cin>>h>>w;
if(h==1&&w==1){
cout<<"First"<<endl;
return 0;
}
if(h==1){
//高さ1の時、例外処理
rep(i,w){
char s;
cin>>s;
if(s=='#'){
if(i%2==0){
cout<<"First"<<endl;
}else{
cout<<"Second"<<endl;
}
return 0;
}
}
if(w%2==0){
cout<<"First"<<endl;
}else{
cout<<"Second"<<endl;
}
return 0;
}
if(w==1){
//幅1の時、例外処理
rep(i,h){
char s;
cin>>s;
if(s=='#'){
if(i%2==0){
cout<<"First"<<endl;
}else{
cout<<"Second"<<endl;
}
return 0;
}
}
if(h%2==0){
cout<<"First"<<endl;
}else{
cout<<"Second"<<endl;
}
return 0;
}
VV vec(h,V(w));//二次元テーブル
rep(i,h){
string s;
cin>>s;
rep(j,w){
if(s[j]=='#'){
vec[i][j]=-2;//壁には-2を入れておく
}
}
}
if(vec[h-1][w-1]==0){
vec[h-1][w-1]=-1;//負けマスには0を入れておきます
}
//以下、端っこで詰むところをメモします
for(int i=h-2;i>=0;i--){
if((vec[i+1][w-1]==-2||vec[i+1][w-1]==1)&&vec[i][w-1]==0){
vec[i][w-1]=-1;
}else if(vec[i+1][w-1]==-1&&vec[i][w-1]==0){
vec[i][w-1]=1;
}
}
for(int i=w-2;i>=0;i--){
if((vec[h-1][i+1]==-2||vec[h-1][i+1]==1)&&vec[h-1][i]==0){
vec[h-1][i]=-1;
}else if(vec[h-1][i+1]==-1&&vec[h-1][i]==0){
vec[h-1][i]=1;
}
}
//やっとDPです、勝ちマスには1を入れます
for(int i=h-2;i>=0;i--){
for(int j=w-2;j>=0;j--){
if(vec[i][j]!=0)continue;
if(vec[i+1][j]==-1||vec[i+1][j+1]==-1||vec[i][j+1]==-1){
vec[i][j]=1;
}else{
vec[i][j]=-1;
}
}
}
if(vec[0][0]==1){
cout<<"First" <<endl;
}else{
cout<<"Second" <<endl;
}
}ABS
- はいDP
- と思いきや、なんとO(1)の解が存在する
- 結局は最後に引いたカードしか使えないんだから、ちまちま取らずにごっそり取ればいい
- 先手目線で考える
- 先手が取れるのは実はN-1番目までかN番目までのカードを全部取る選択肢だけ
- というのも、それ以外を選択しても、後手の操作によって結果は変わらないから
- ゆえに答えはmin(|a[N]-W|,|a[N]-a[N-1]|)
コード例
int main(){
ll n,z,w;
cin>>n>>z>>w;
V vec(n);
rep(i,n)cin>>vec[i];
ll res=abs(vec[n-1]-w);
if(n>=2)chmax(res,abs(vec[n-1]-vec[n-2]));
cout<<res<<endl;
}有向グラフと数
Difficulty銅なんてわからないに決まってんだろ- 強い人向けです
- どうやら後退解析を用いるらしいです
-
AtCoder ARC 038 D - 有向グラフと数 - けんちょんの競プロ精進 ...
- ↑の記事で紹介されてます
コード例
#include <iostream>
#include <vector>
#include <queue>
using namespace std;
// グラフの頂点数、辺数、各ノードの重み
int N, M;
vector<int> X;
// ゲームグラフ (後退解析のために辺の向きを逆にする)
vector<vector<int> > G;
vector<int> deg; // ゲームグラフにおける出次数 (辺の向きを逆にした状態で入次数)
// 二分探索判定 (D 以上にできるかどうか)
bool judge(int D) {
vector<int> cdeg = deg;//この場限りの出次数
queue<int> que; // キュー
vector<int> dp(N * 2, -1); // 最初は全体を -1 で初期化
// 初期条件、分かった頂点からqueueに突っ込んで伸ばしていくぞい
for (int i = 0; i < N; ++i) {
if (X[i] >= D) {
dp[i] = 1; // 先手勝ち
que.push(i);
if (cdeg[i] == 0) {
dp[i + N] = 0; // 後手負け これ以上動けないため
que.push(i + N);
}
}
else {
dp[i + N] = 1; // 後手勝ち
que.push(i + N);
if (cdeg[i] == 0) {
dp[i] = 0; // 先手負け
que.push(i);
}
}
}
// 後退解析 (ここは自動的に書ける)
while (!que.empty()) {
int v = que.front(); que.pop();//幅優先と同じ要領
for (auto nv : G[v]) {
// すでに見た頂点はスルー
if (dp[nv] != -1) continue;
--cdeg[nv]; // 辺 (nv, v) を削除
if (dp[v] == 0) {//遷移先が相手にとって負け確だったら
dp[nv] = 1;//今いるところは勝確!
que.push(nv);//その状態から、さらに前を見るぞ
}
else if (dp[v] == 1) {//相手が勝ちの時…
if (cdeg[nv] == 0) {
//もし相手の勝ち状態にしか遷移できなかったら…
dp[nv] = 0;//その状態は負け!
que.push(nv);//その状態から、さらに前を見るぞ
}
}
}
}
// ノード 0 が先手番で勝ちかどうか
return (dp[0] == 1);
}
//状態数は頂点数*2(先手と後手)
int main() {
// 入力
cin >> N >> M;
X.resize(N*2);
for (int i = 0; i < N; ++i) cin >> X[i];
for (int i = 0; i < N; ++i) X[i+N] = X[i];
G.assign(N*2, vector<int>());
deg.assign(N*2, 0);
for (int i = 0; i < M; ++i) {
int a, b; cin >> a >> b; --a, --b;
G[b + N].push_back(a); // 後手番での後退遷移
G[b].push_back(a + N); // 先手番での後退遷移
deg[a]++; deg[a + N]++;
}
// 二分探索
int low = 0, high = 1000000007; // low: 絶対先手勝つ、high: 絶対先手負ける
while (high - low > 1) {
int mid = (low + high) / 2;
if (!judge(mid)) high = mid;
else low = mid;
}
cout << low << endl;
}終わり!!
deck
By zeke8080
deck
- 234

