基礎圖論
專有名詞簡介
節點
就是圖上的每個點
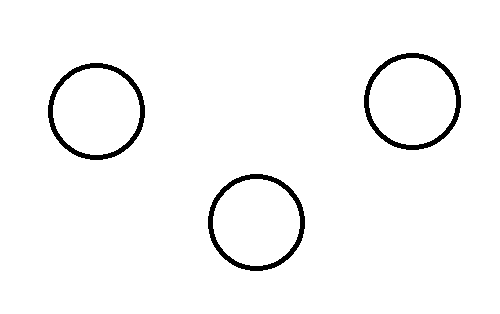
邊
點與點之間的連線


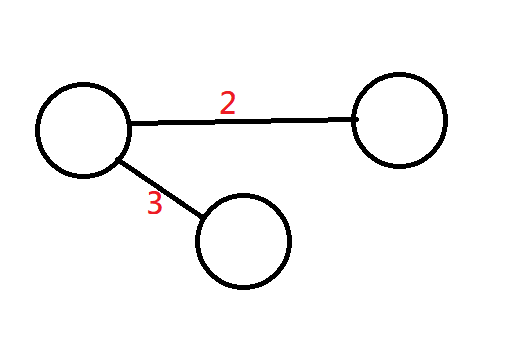
邊權
邊上所帶的數字,常常用來表示時間或是花費


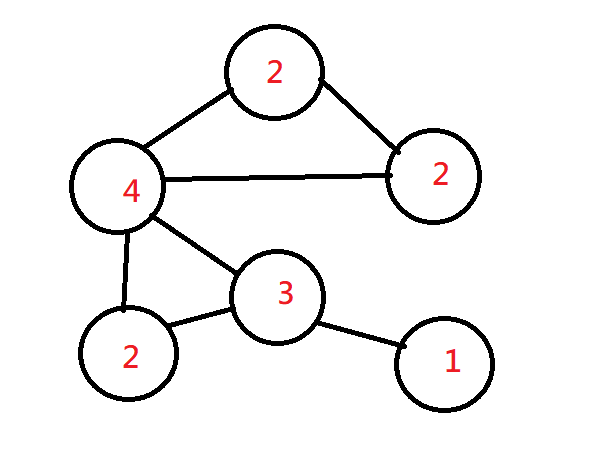
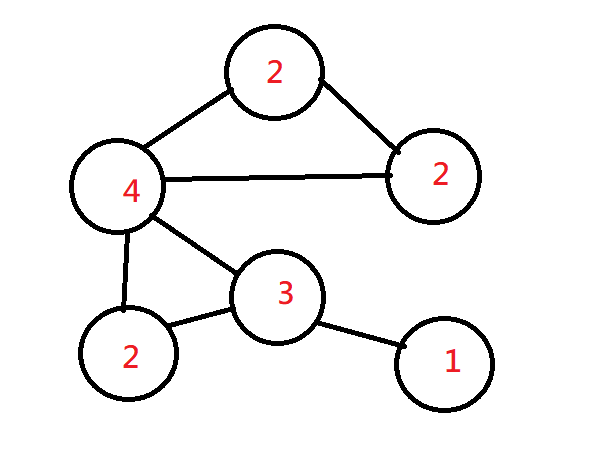
點權
點上所帶的數字,常常用來表示花費



度數
一個點所連到的邊數
環
一條頭尾同點的連線

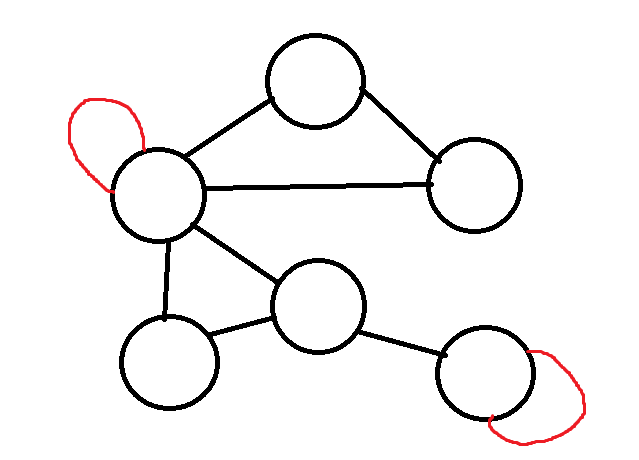
自環
就是連到自己的邊



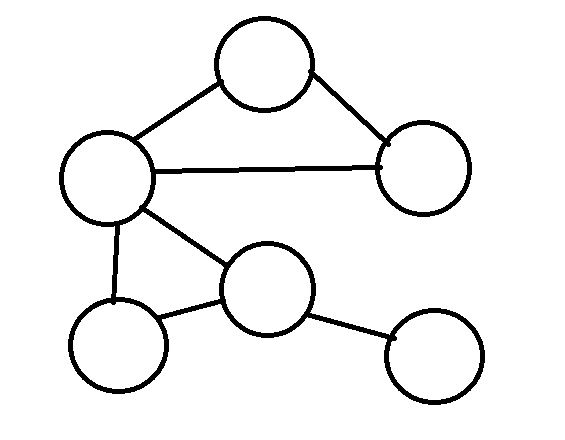
無向圖
邊沒有方向的圖




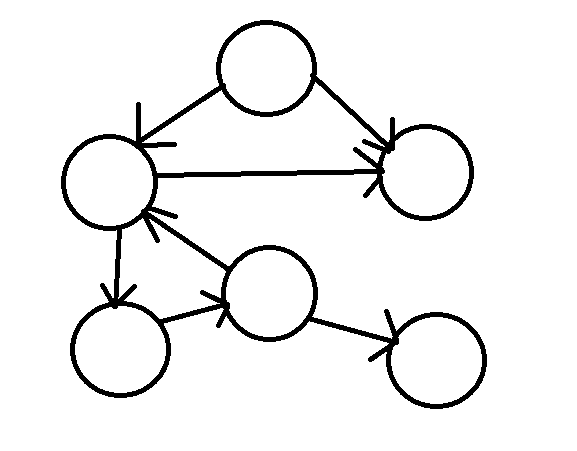
有向圖
邊有方向的圖





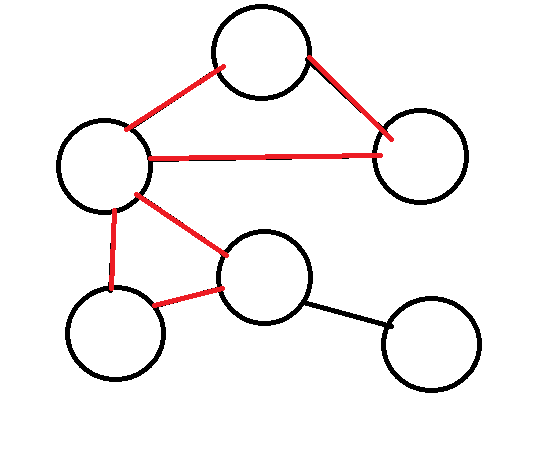
路徑
連續邊的序列






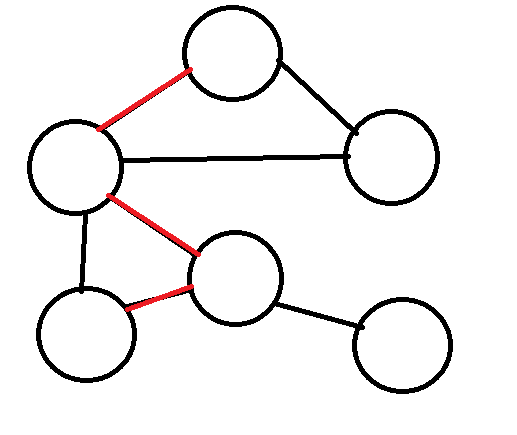
路徑
連續邊的序列







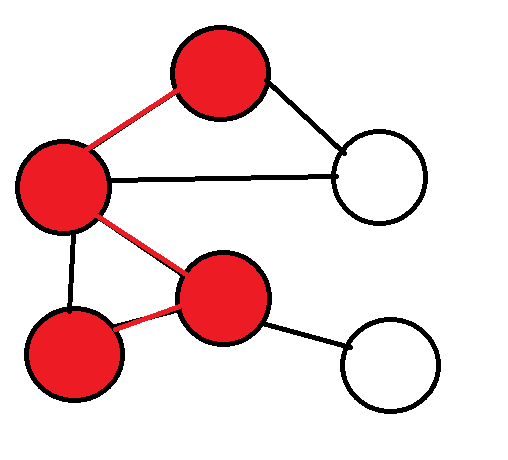
子圖
一個圖中的選某些點與邊構成的圖(也可以全選or不選)







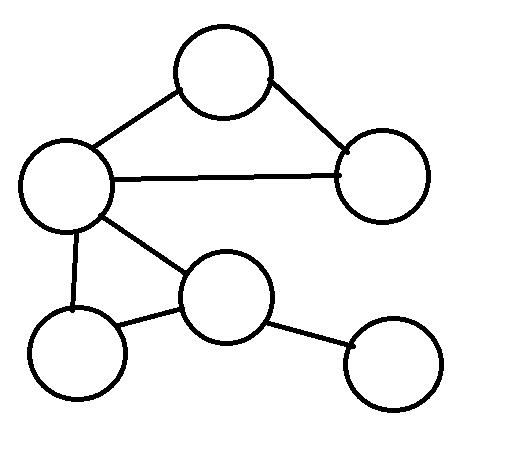
圖的表示法
在程式中表達一張圖?
Text
在程式中表達一張圖?
Text

鄰接矩陣
利用一般的陣列,一一對應表達(此為是否連線)
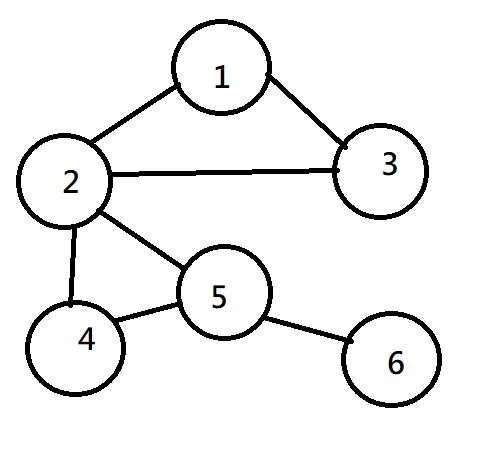
| 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|
| 1 | 0 | 1 | 1 | 0 | 0 | 0 |
| 2 | 1 | 0 | 1 | 1 | 1 | 0 |
| 3 | 1 | 1 | 0 | 0 | 0 | 0 |
| 4 | 0 | 1 | 0 | 0 | 1 | 0 |
| 5 | 0 | 1 | 0 | 1 | 0 | 1 |
| 6 | 0 | 0 | 0 | 0 | 1 | 0 |
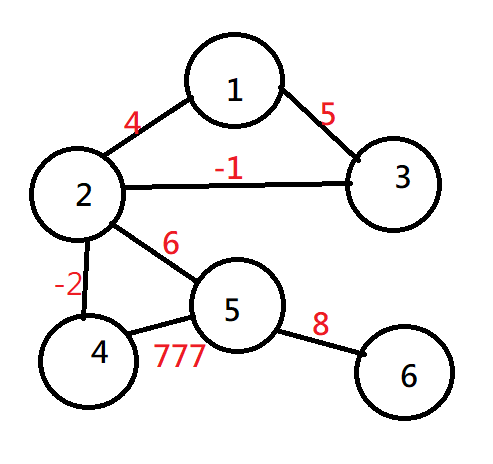
鄰接矩陣
利用一般的陣列,一一對應表達(此為邊權)

| 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|
| 1 | 0 | 4 | 5 | 0 | 0 | 0 |
| 2 | 4 | 0 | -1 | -2 | 6 | 0 |
| 3 | 5 | -1 | 0 | 0 | 0 | 0 |
| 4 | 0 | -2 | 0 | 0 | 777 | 0 |
| 5 | 0 | 6 | 0 | 777 | 0 | 8 |
| 6 | 0 | 0 | 0 | 0 | 8 | 0 |
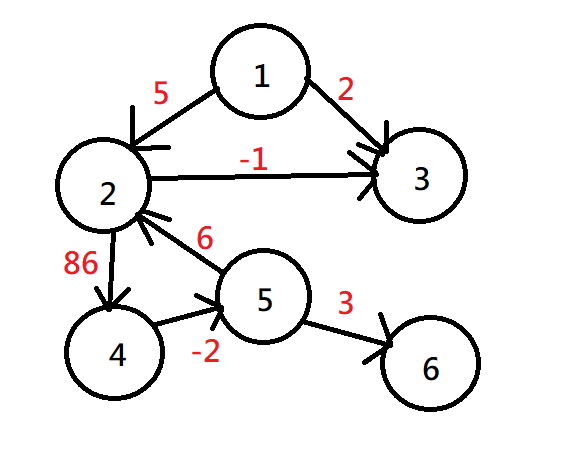
鄰接矩陣
利用一般的陣列,一一對應表達(此為有向圖、邊權)

| 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|
| 1 | 0 | 5 | 2 | 0 | 0 | 0 |
| 2 | 0 | 0 | -1 | 86 | 0 | 0 |
| 3 | 0 | 0 | 0 | 0 | 0 | 0 |
| 4 | 0 | 0 | 0 | 0 | -2 | 0 |
| 5 | 0 | 6 | 0 | 0 | 0 | 3 |
| 6 | 0 | 0 | 0 | 0 | 0 | 0 |

int G[N][N];
for (int i = 1; i <= n; i++) {
int a, b;
cin >> a >> b;
G[a][b] = 1;
//沒邊權
}
for (int i = 1; i <= n; i++) {
int a, b, w;
cin >> a >> b >> w;
G[a][b] = w;
//帶邊權
}不過她的空間複雜度太多,容易爆掉(N^2)
鄰接串列
利用vector儲存一個點連出去的其他點,有向圖同理

| 1 | 2 | 3 | ||
| 2 | 1 | 3 | 4 | 5 |
| 3 | 1 | 2 | ||
| 4 | 2 | 5 | ||
| 5 | 2 | 4 | 6 | |
| 6 | 5 |
鄰接串列
如果有權重的話,可以利用pair來存值

| 1 | (2,4) | (3,5) | ||
| 2 | (1,4) | (3,-1) | (4,-2) | (5,6 |
| 3 | (1,5) | (2,-1) | ||
| 4 | (2,-2) | (5,777) | ||
| 5 | (2,6) | (4,777) | (6,8) | |
| 6 | (5,8) |

vector<int> vec[N];
for (int i = 0; i < m; ++i) {
int a, b;
cin >> a >> b;
vec[a].push_back(b);
} // 不帶權
vector<pair<int,int>> v[N];
for (int i = 0; i < m; ++i) {
int a, b, w;
cin >> a >> b >> w;
vec[a].push_back({b,w});
vec[b].push_back({a,w});
} // 帶權圖的遍歷法
怎麼跑完整張圖?
DFS(深度優先搜尋)
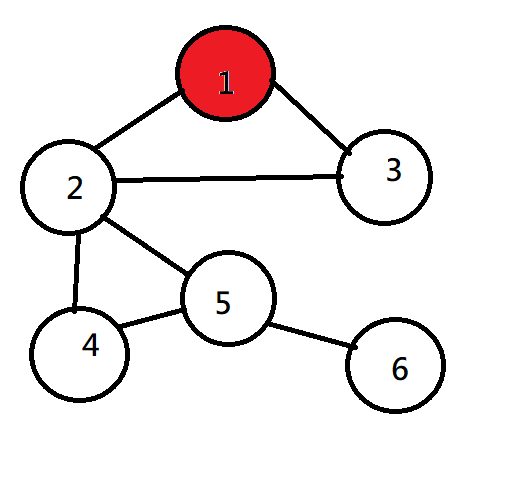
| 1 | 2 | 3 | ||
| 2 | 1 | 3 | 4 | 5 |
| 3 | 1 | 2 | ||
| 4 | 2 | 5 | ||
| 5 | 2 | 4 | 6 | |
| 6 | 5 |
DFS(深度優先搜尋)
| 1 | 2 | 3 | ||
| 2 | 1 | 3 | 4 | 5 |
| 3 | 1 | 2 | ||
| 4 | 2 | 5 | ||
| 5 | 2 | 4 | 6 | |
| 6 | 5 |
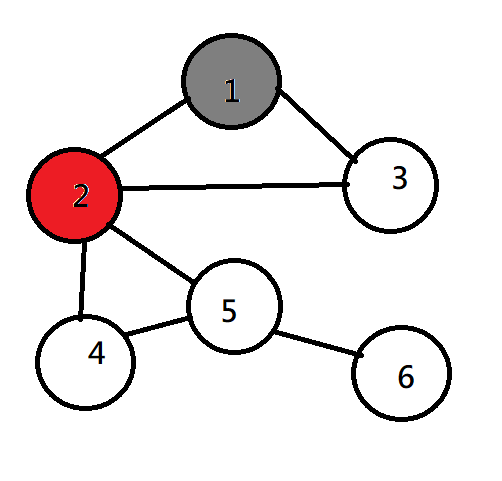
DFS(深度優先搜尋)
| 1 | 2 | 3 | ||
| 2 | 1 | 3 | 4 | 5 |
| 3 | 1 | 2 | ||
| 4 | 2 | 5 | ||
| 5 | 2 | 4 | 6 | |
| 6 | 5 |
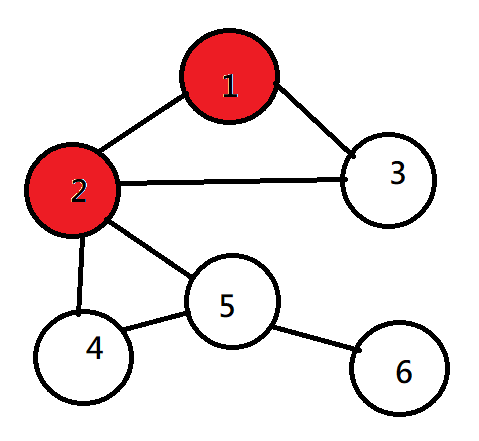
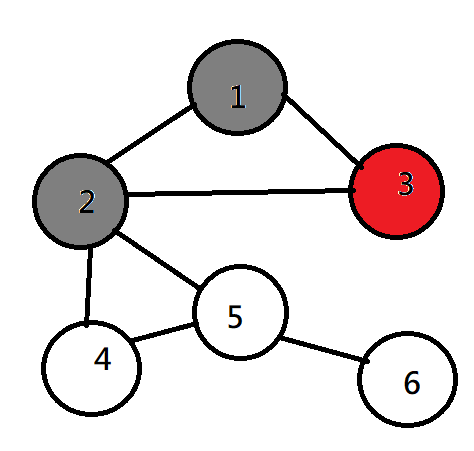
DFS(深度優先搜尋)
| 1 | 2 | 3 | ||
| 2 | 1 | 3 | 4 | 5 |
| 3 | 1 | 2 | ||
| 4 | 2 | 5 | ||
| 5 | 2 | 4 | 6 | |
| 6 | 5 |
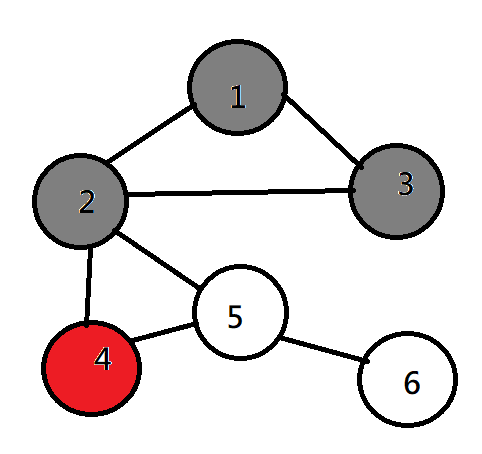
DFS(深度優先搜尋)
| 1 | 2 | 3 | ||
| 2 | 1 | 3 | 4 | 5 |
| 3 | 1 | 2 | ||
| 4 | 2 | 5 | ||
| 5 | 2 | 4 | 6 | |
| 6 | 5 |
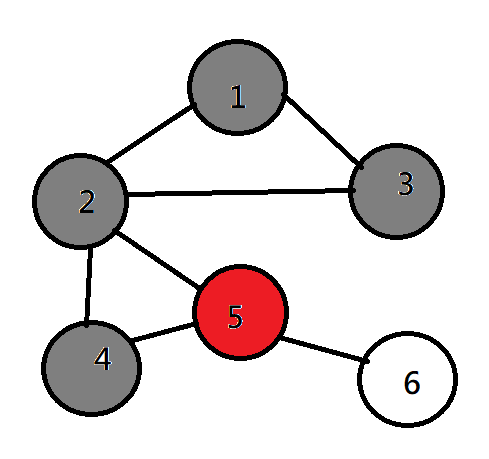
DFS(深度優先搜尋)
| 1 | 2 | 3 | ||
| 2 | 1 | 3 | 4 | 5 |
| 3 | 1 | 2 | ||
| 4 | 2 | 5 | ||
| 5 | 2 | 4 | 6 | |
| 6 | 5 |
bool vis[N];
vector<int> vec[N];
void dfs(int x) {
vis[x] = 1;
for (int i:vec[x]) {
if (!vis[i]) dfs(i);
}
for(int i=0;i<vec[x].size();i++) {
if (!vis[vec[i]]) dfs(vec[i]);
}
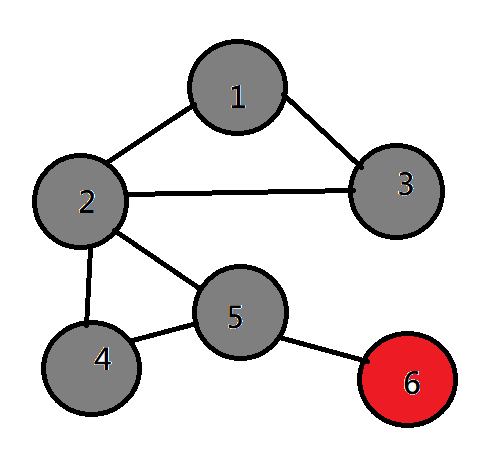
}BFS(廣度優先搜尋)
| 1 | 2 | 3 | ||
| 2 | 1 | 5 | ||
| 3 | 1 | |||
| 4 | 5 | |||
| 5 | 2 | 4 | 6 | |
| 6 | 5 |
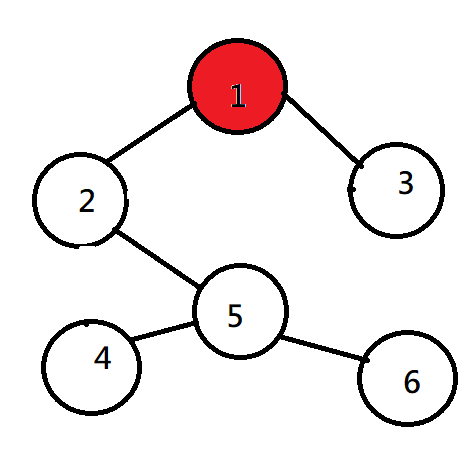
BFS(廣度優先搜尋)
| 1 | 2 | 3 | ||
| 2 | 1 | 5 | ||
| 3 | 1 | |||
| 4 | 5 | |||
| 5 | 2 | 4 | 6 | |
| 6 | 5 |
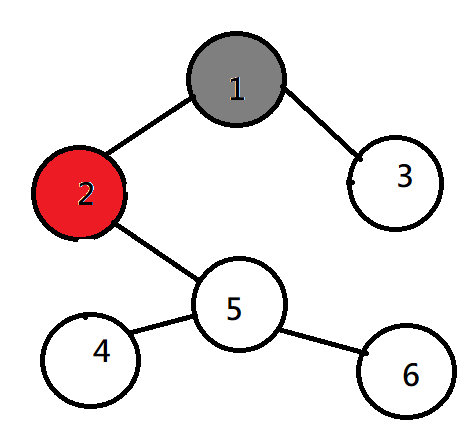
BFS(廣度優先搜尋)
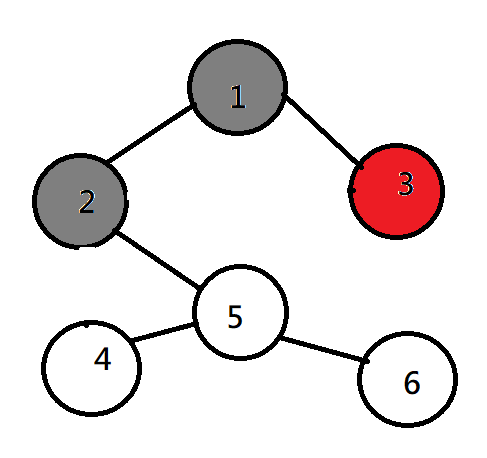
| 1 | 2 | 3 | ||
| 2 | 1 | 5 | ||
| 3 | 1 | |||
| 4 | 5 | |||
| 5 | 2 | 4 | 6 | |
| 6 | 5 |
BFS(廣度優先搜尋)
| 1 | 2 | 3 | ||
| 2 | 1 | 5 | ||
| 3 | 1 | |||
| 4 | 5 | |||
| 5 | 2 | 4 | 6 | |
| 6 | 5 |
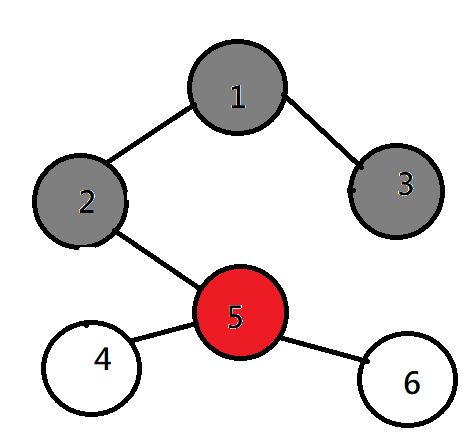
BFS(廣度優先搜尋)
| 1 | 2 | 3 | ||
| 2 | 1 | 5 | ||
| 3 | 1 | |||
| 4 | 5 | |||
| 5 | 2 | 4 | 6 | |
| 6 | 5 |
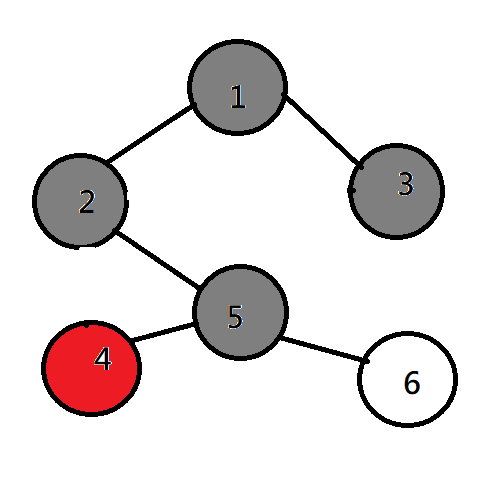
BFS(廣度優先搜尋)
| 1 | 2 | 3 | ||
| 2 | 1 | 5 | ||
| 3 | 1 | |||
| 4 | 5 | |||
| 5 | 2 | 4 | 6 | |
| 6 | 5 |
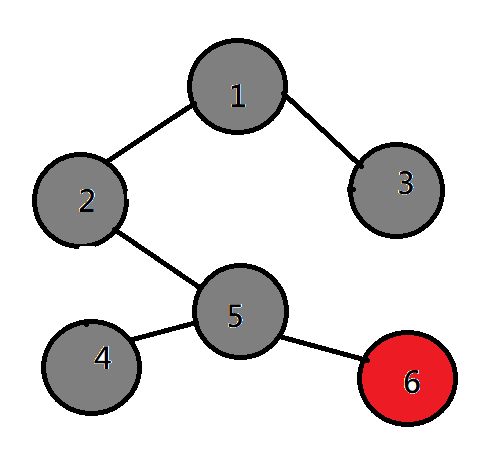
vector<int> vec[N];
bool vis[N];
queue<int> que;
void BFS(int x){
for(int i:vec[x]){
if(!vis[i]){
vis[i]=1;
que.push(i);
}
}
if(que.size()){
int u = que.front();
que.pop();
BFS(u);
}
}Fire! BFS
Fire In The Forest
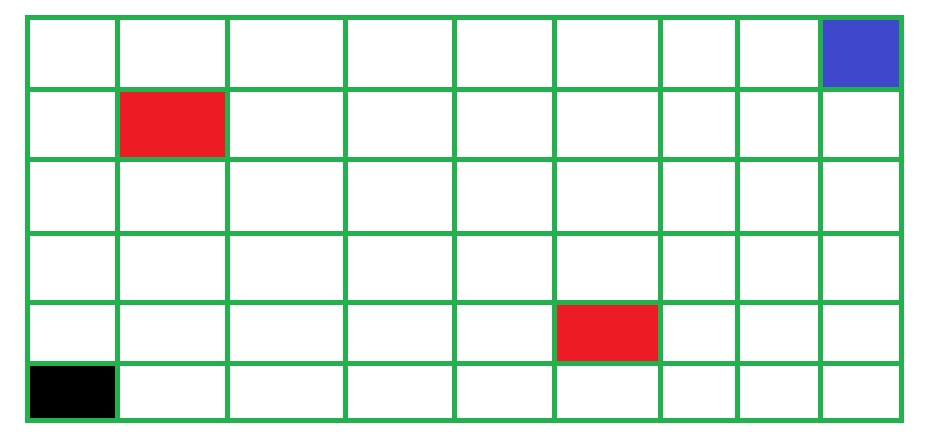
藍色是起點、黑色是目標、紅色是大火
Fire In The Forest
一秒後,森林的情況
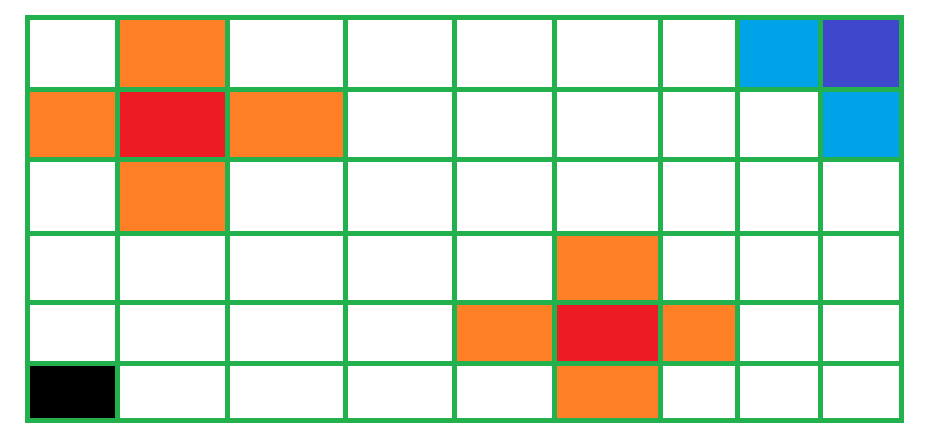
Fire In The Forest
兩秒後,森林的情況
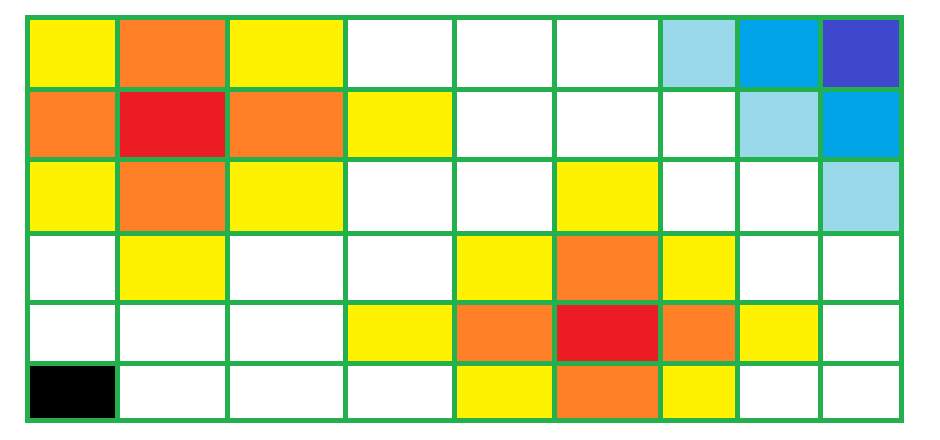
Fire In The Forest
三秒後,森林的情況
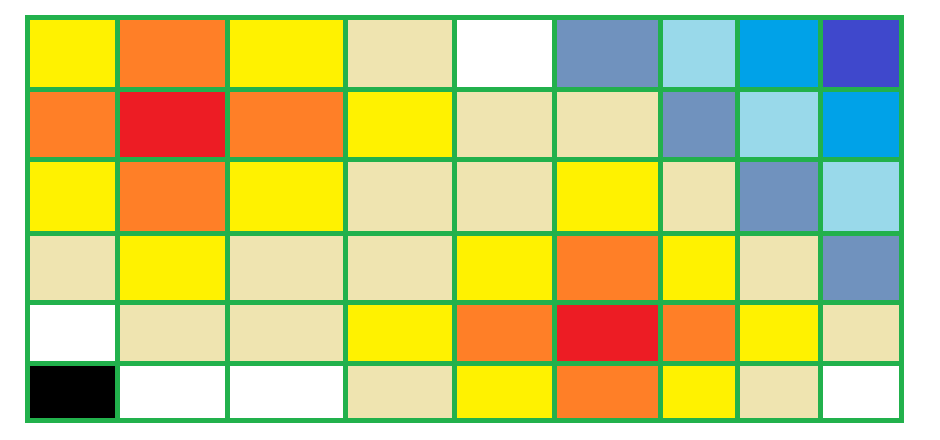
Fire In The Forest
維護的是「人在第T秒可以走到的地方」與
「火在第T秒會燒到的地方」
火先燒,人再走=>火先放進Queue再放人

基礎圖論
By Zhe_侑哲 You
基礎圖論
- 206


