Robust control of Boolean networks in systems biology
Sam Pastva,
with Eva Šmijáková, David Šafránek, and Luboš Brim
Modelling gene interactions
Gene X @DNA
Gene X @mRNA
Protein X
Gene Y @DNA
Gene Y @mRNA
Protein Y
\(\oplus\)
\(\ominus\)
Gene X
Gene Y
Gene Regulatory Network (GRN)
Gene X
Gene A
Gene B
Gene C
Do we need both A and C, or just one? Does B interact with A and C equally or not?
A
C
B
f_{A}(x) = \neg x_{C}
x \in \{0,1\}^n~\text{(state)}
f_{B}(x) = x_{A}
f_{C}(x) = x_{C} \lor (x_{A} \land \neg x_{B})
Boolean Network (BN)
f_{A}(x) = \neg x_{C}
f_{B}(x) = x_{A}
f_{C}(x) = x_{C} \lor (x_{A} \land \neg x_{B})
000
100
111
011
001
Synchronous update: all updates happen at the same time.
000
100
110
101
001
111
011
Asynchronous update: better captures unknown time-scales of processes.
What "outcomes" are possible in our model? (Attractors - bottom SCCs)
- Single state (fixed-point attractor)
- Larger region (complex attractor)
- cycle (oscillation)
- other (disorder)
110
110
110
110
110
110
110
110
110
Assumption: chemistry is fair. Only terminal states/components can be attractors.
Different attractors can represent different biological functionality (phenotype).
Addressing model uncertainty
- Logical parameters (network inputs)
- Functional parameters (uninterpreted function)
Gene X
Gene Y
Input A
f_{C}(x) = x_{C} \lor {\color{red} F(x_{A}, x_{B})}
Exponentially many "parametrisations" for logical parameters, double exponential for functional parameters.
Benes, N., Brim, L., Pastva, S., Polácek, J., & Šafránek, D. (2019). Formal Analysis of Qualitative Long-Term Behaviour in Parametrised Boolean Networks. ICFEM.
Control of Boolean networks
- Non-determinism is widespread;
- Classical stabilisation may not be feasible (nor desired);
- Full control is largely unnecessary;
- Output control is more suitable, but can still include biologically unrealistic cases;
- Observability is (in theory) high, but suffers from large delays;
- Every intervention is very costly;
- Interventions (mostly) cannot be applied indefinitely.
(The problems of )
Classical control theory for BNs
Boolean network "target" control
Target
Target can mean slightly different things, depending on biological context, model, etc...
- A specific attractor(s) (exact set of states)
- Attractor state (must appear in the final attr.)
- A larger "subspace" (also called phenotype)
Optionally, source can be specified too: control must work in all source states.
Source
Regardless, target must admit some trap set in which the model can stay indefinitely.
Controlling through perturbations
One-step perturbation (e.g. short-term treatment)
110
001
000
010
Temporary perturbation (e.g. long-term treatment)
001
011
111
101
100
Permanent perturbation (e.g. mutation)
101
010
110
111
100
Perturbation forces a subset of variables to a constant high/low state.
One-step
Target
Source
Baudin, Alexis, et al. "Controlling large Boolean networks with single-step perturbations." Bioinformatics 35.14 (2019): i558-i567.
Temporary
Target
×
×
×
Su, Cui, Soumya Paul, and Jun Pang. "Controlling large Boolean networks with temporary and permanent perturbations." FM 2019.
Source
Permanent
Target
×
×
Su, Cui, Soumya Paul, and Jun Pang. "Controlling large Boolean networks with temporary and permanent perturbations." FM 2019.
Source
To minimize biological "burden" on the system, a perturbation must be as small (simple) as possible.
In practice, minimal perturbations are often small!
Additional steps are needed to asses biological viability of perturbations!
What perturbations do
we actually want?
What about partially unknown networks?
Whether a perturbation works depends on the valuation of logical and functional parameters.
A small perturbation that works only sometimes
may be too unreliable.
A large perturbation that works always
may not be biologically viable.
Perturbation robustness
# parameter valuations where perturbation p achieves control
# parameter valuations that admit the desired target
robustness(p) =
A good perturbation is not only small, but also robust.
Brim, Luboš, et al. "Temporary and permanent control of partially specified Boolean networks." Biosystems 223 (2023): 104795.
How to compute robust perturbations?
Binary Decision Diagrams
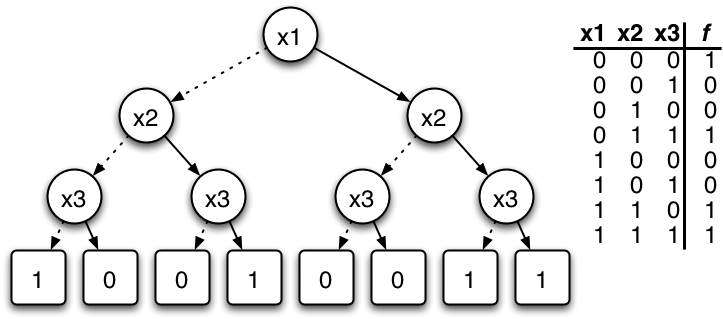
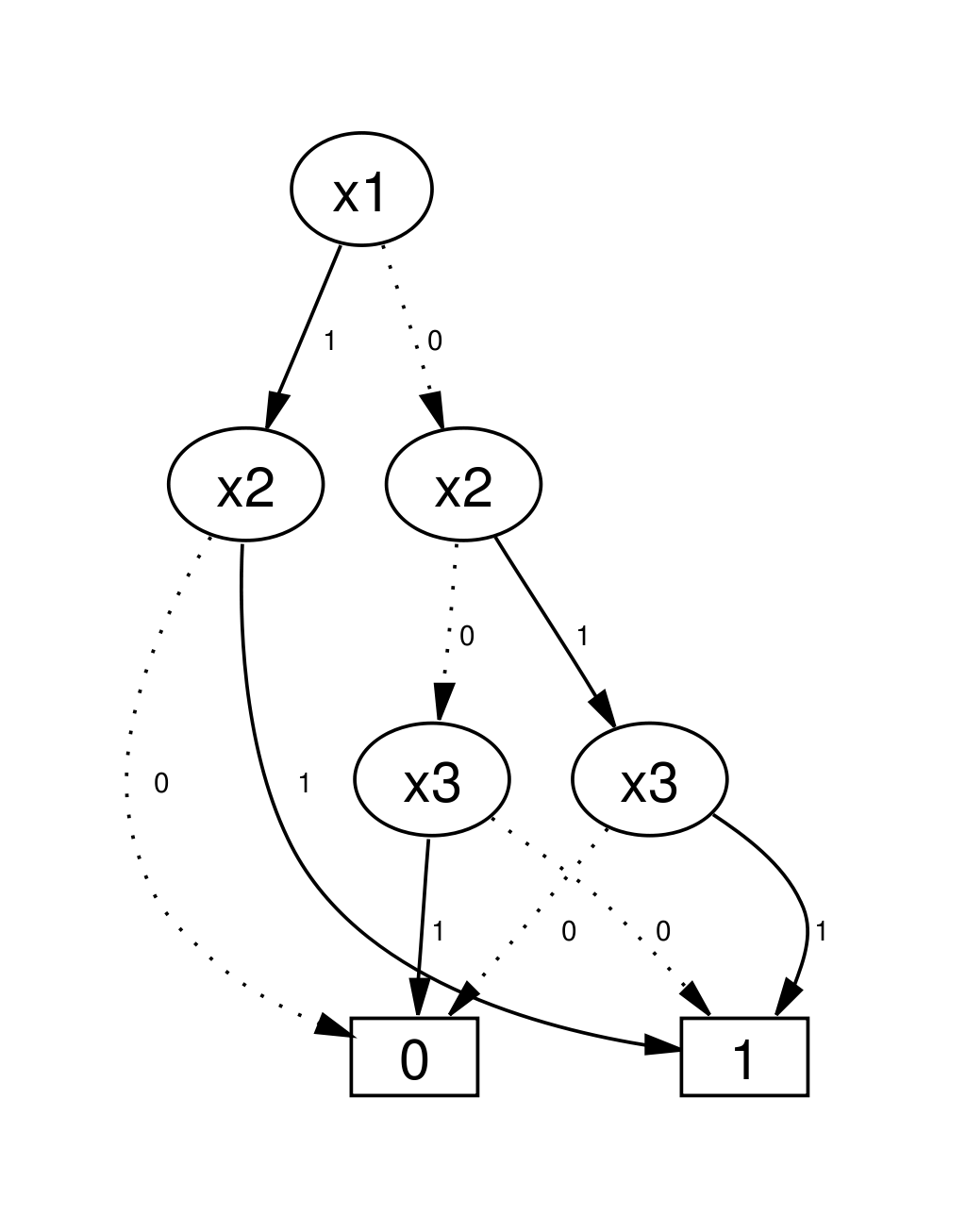
Parametrisation+State of a BN is a bit-vector. Sets/relations of these can be encoded via Boolean functions.
s \in X \Leftrightarrow f_{BDD(X)}(s) = 1~(\text{with}~X \subseteq \{0,1\}^{k})
Set operations correspond to logical operations on functions (and graph operations on BDDs)
X \cap Y \equiv f_{BDD(X)} \land f_{BDD(Y)}
Since Boolean network is described by Boolean functions, computing successors/predecessors (including parameters) is relatively straightforward.
Benes, N., Brim, L., Pastva, S., Polácek, J., & Šafránek, D. (2019). Formal Analysis of Qualitative Long-Term Behaviour in Parametrised Boolean Networks. ICFEM.
Symbolic encoding of perturbations
A perturbation is treated as another type of parameter:
f_{C}(x) = x_{C} \lor {\color{red} F(x_{A}, x_{B})}
\hat{f}_{C}(x) = ({\color{orange} p_{C}} \Rightarrow x_{C}) \land ({\color{orange} \neg p_{C}} \Rightarrow f_{C}(x))
"Perturbation parameters" need to be differentiated from "uncertain" parameters (i.e. during robustness assessment).
"Naive" encoding uses two "bits" per variable. Here we show that algorithms also exist for a simpler "one bit" encoding.
Brim, Luboš, et al. "Temporary and permanent control of partially specified Boolean networks." Biosystems 223 (2023): 104795.
Target
Strong basin
Target
×
×
×
Strong basin
Perturbed strong basin
(of the strong basin)
Source
Result: A symbolic relation (a BDD) with all viable perturbations for all viable parametrisations.
We can "search" this relation to find minimal perturbations, robust perturbations, or both.
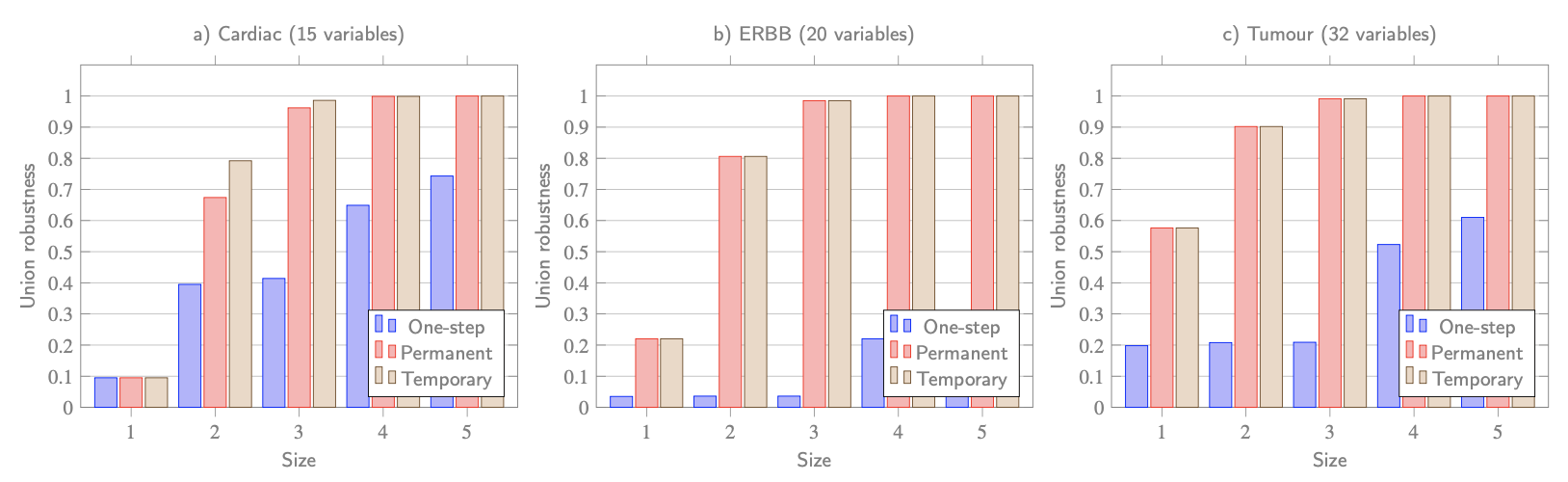
Back to robustness...
*up to 10^9 parameter valuations/model
Algorithm runs symbolically for all perturbations and parametrisations.
Conclusion
- Classical control theory is not well equipped to handle "logical" models in systems biology.
- Various notions of target (or source-target) control are evolving to cover this need.
- Here, small perturbations are typically sufficient to achieve the desired target.
- However, uncertainty is often needed in biological models ⇒ partially specified Boolean networks.
- A good perturbation is not only small, but also robust.
- Symbolic methods are a viable starting point, but further research is needed!
- Minimal perturbations typically aren't robust, but robust perturbations can still be small.
Robust control of Boolean networks in systems biology
By Samuel Pastva
