Variable Stabilisation in Boolean Monotonic

Model Pools

Samuel Pastva

Signed Influence Graph (\(IG\))

  • Directed graph of variables with assigned influence monotonicity.
  • Every influence is either positive or negative (for better or worse).
  • \(dep^{\oplus}(v_i)\): positive influences.
  • \(dep^{\ominus}(v_i)\): negative influences.

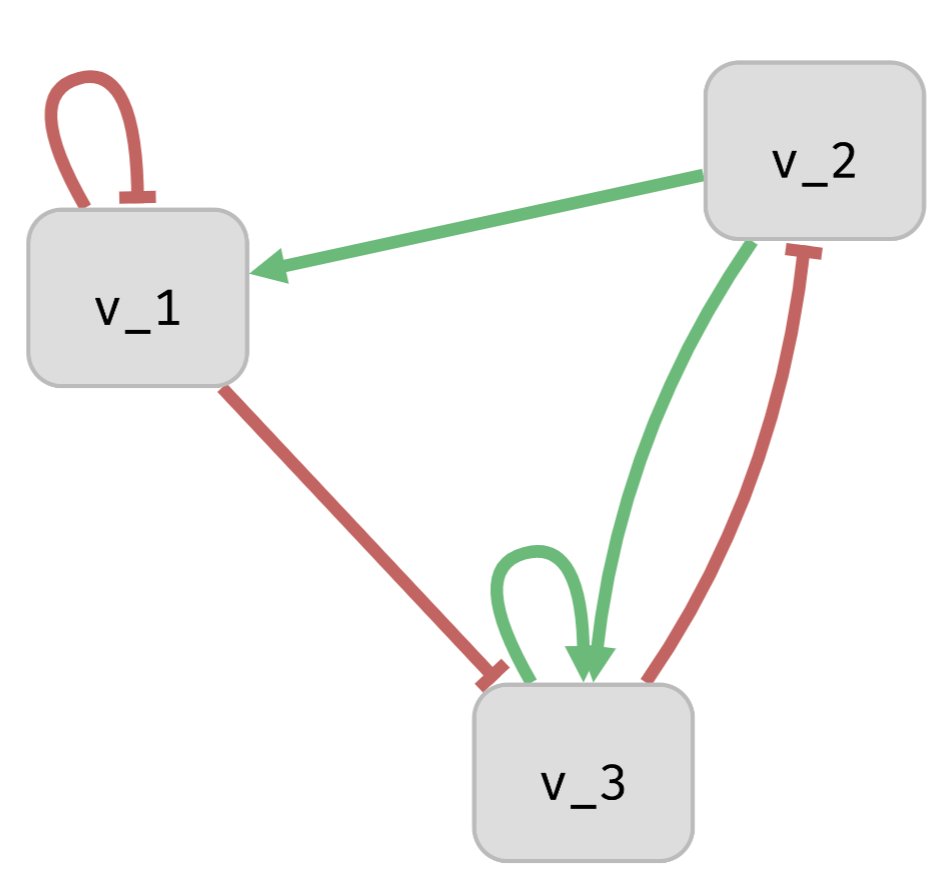
Monotonic Boolean network (\(BN\))

  • Collection of Boolean functions \((F_1, \ldots, F_n)\) that define the dynamics of variables \((v_1, \ldots, v_n)\).
  • Each \(F_i\) is assumed to be monotonic in all inputs.
  • Functions are applied asynchronously to the network state (\(x \in \mathbb{B}^n\)), resulting in \(ASTG(BN)\).
  • \(dep^{\oplus}(F_i)\): positive inputs.
  • \(dep^{\ominus}(F_i)\): negative inputs.
\begin{matrix} F_1(x) = & \overline{x_1} \land x_2 \\ F_2(x) = & \overline{x_3} \\ F_3(x) = & x_3 \lor (\overline{x_1} \land x_2) \end{matrix}

A Boolean network is consistent with a signed interaction graph, \(BN \models IG\), when dependencies of \(F_i\) agree with dependencies of \(v_i\).

dep^{\oplus}(F_i) \subseteq dep^{\oplus}(v_i) \\ dep^{\ominus}(F_i) \subseteq dep^{\ominus}(v_i) \\
\begin{matrix} F_1(x) = & \overline{x_1} \land x_2 \\ F_2(x) = & \overline{x_3} \\ F_3(x) = & x_3 \lor (\overline{x_1} \land x_2) \end{matrix}

Many different functions can be consistent with the same influence graph:

\begin{matrix} F_1(x) = & \overline{x_1} \lor x_2 \\ F_2(x) = & \overline{x_3} \\ F_3(x) = & (x_3 \land \overline{x_1}) \lor x_2 \end{matrix}
\begin{matrix} F_1(x) = & \overline{x_1} \land x_2 \\ F_2(x) = & \overline{x_3} \\ F_3(x) = & x_3 \lor (\overline{x_1} \land x_2) \end{matrix}

...

Not all influences within the IG have to be used by the BN:

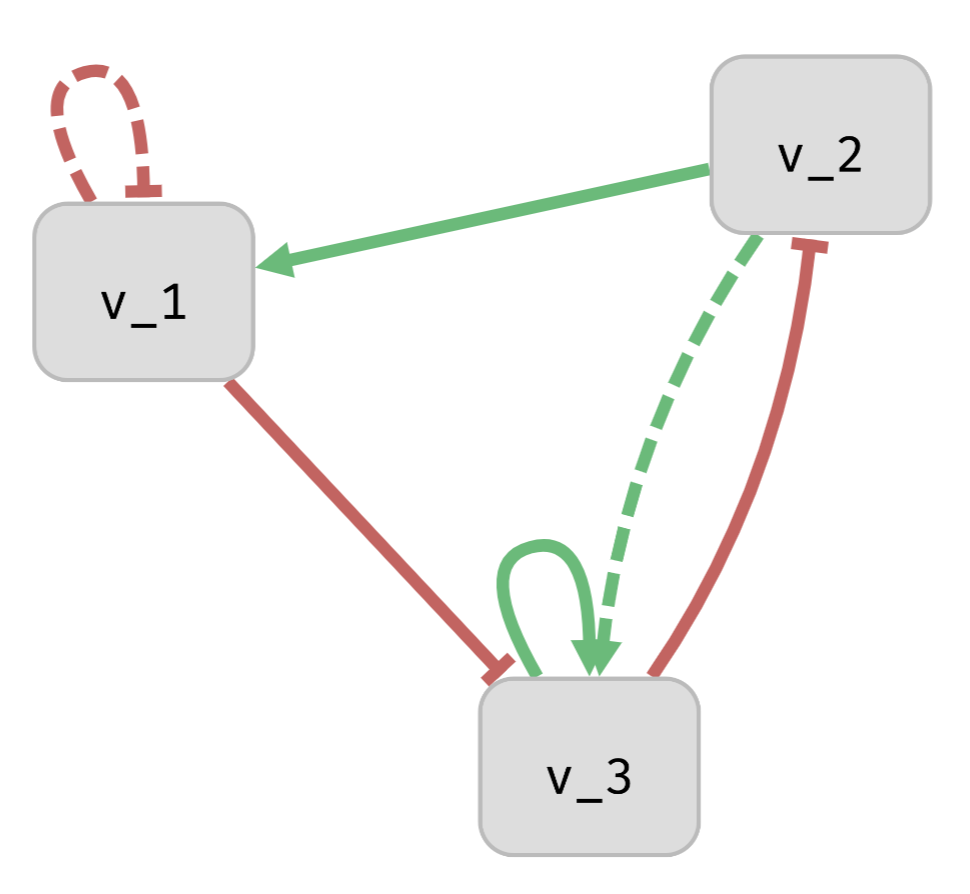
\begin{matrix} F_1(x) = & x_2 \\ F_2(x) = & \overline{x_3} \\ F_3(x) = & x_3 \lor \overline{x_1} \end{matrix}

Monotonic model pool \(M(IG)\): All Boolean networks \(BN\) s.t. \(BN \models IG\).

Which properties appear due to the influence graph and which are due to the choice of update functions?

Schwieger, Robert, and Heike Siebert. "Structure and behavior in Boolean monotonic model pools." Biosystems 214 (2022): 104610.

2 419 200 networks in the monotonic pool.

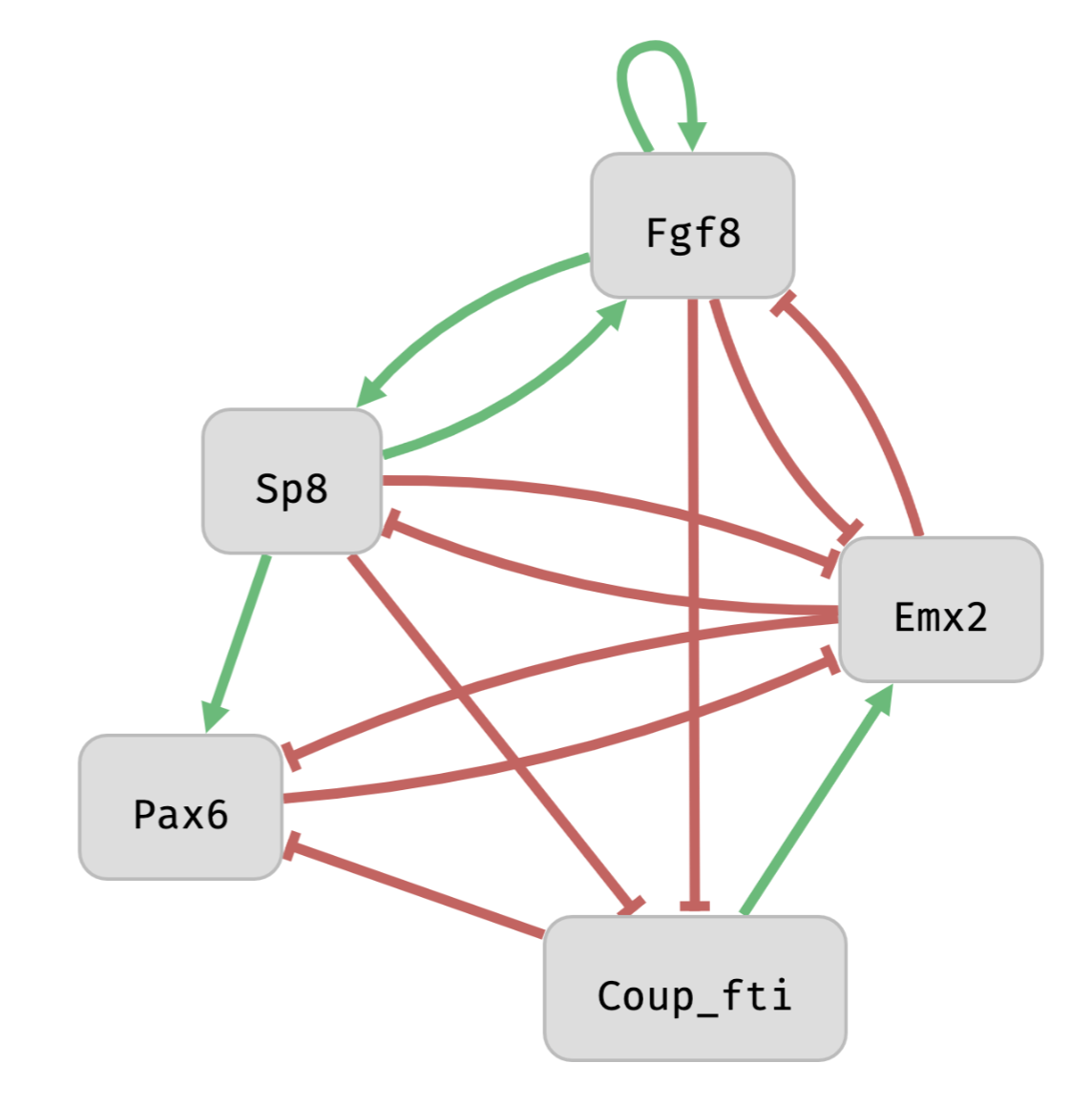
No complex attractor. Only fixed-points.

Why?

Thomas Conjectures (or other static analysis)

  • If IG has no cycle, there is a single fixed-point attractor.
  • If IG has no positive cycle (even parity), there is exactly one attractor.
  • If IG has no negative cycle (odd parity), there are no cyclic attractors.
  • ...

Paulevé, Loïc, and Adrien Richard. "Static analysis of Boolean networks based on interaction graphs: a survey." Electronic Notes in Theoretical Computer Science 284 (2012): 93-104.

Thomas conjectures capture "analytical" properties of \(M(IG)\). How else can we study \(M(IG)\)?

Skeleton network of \(M(IG)\)

A Boolean network \(\Gamma(IG)\) consisting of functions \(\Gamma_1, \ldots, \Gamma_n\) where:

Schwieger, Robert, and Heike Siebert. "Structure and behavior in Boolean monotonic model pools." Biosystems 214 (2022): 104610.

\Gamma_i(x) = x_i \nLeftrightarrow \big[ \bigvee_{j \in dep^{\oplus}(i)} x_i \nLeftrightarrow x_j \lor \bigvee_{j \in dep^{\ominus}(i)} x_i \Leftrightarrow x_j \big]

A transition exists in \(ASTG(\Gamma)\) if \(x_i \nLeftrightarrow x_j\) (for positive dependency) or \(x_i \Leftrightarrow x_j\) (for negative dependency).

Over-approximation of monotonic pools

Original: The \(ASTG(\Gamma)\) is the union of the quotient graphs of every \(BN \in M(IG)\).

New: The \(ASTG(\Gamma)\) is the union of the \(ASTG(BN)\) for every \(BN \in M_{[!]}(IG)\) (a strict monotonic pool).

Strict pool: If a variable has at least one dependency, it cannot be constant (true/false).

Let BN be an arbitrary network from \(M_{[!]}(IG)\). Corollary:

  • If \(x \nrightarrow y\) in \(ASTG(\Gamma)\), then \(x \nrightarrow y\) in \(ASTG(BN)\).
  • If \(X \subseteq \mathbb{B}^n\) is SCC-closed in \(ASTG(\Gamma)\), then \(X\) is SCC-closed in \(ASTG(BN)\).
  • If \(X \subseteq \mathbb{B}^n\) is a trap set in \(ASTG(\Gamma)\), then \(X\) is a trap set in \(ASTG(BN)\).

The approximation is still very broad: For example, every acyclic \(IG\) produces an acyclic \(ASTG\). However, \(ASTG(\Gamma)\) of such \(IG\) often contains cycles.

Is there a practical use for skeleton networks?

Skeleton network is a "normal" BN that can be processed using existing tools and algorithms (AEON, GINsim, pystablemotifs, ... ).

In this case, Python interface of AEON is used to run analysis with BDD-based symbolic representation.

The skeleton network has two fixed-point attractors.

These are guaranteed to appear in every network of the (strict) monotonic pool.

Observably stable variable

For some initial conditions, the network variable never changes its value.

(Minimal) stabilising intervention

By fixing a (minimal) subset of network variables, all variables become observably stable.

Performing such intervention introduces stability to otherwise unstable variables.

Computation

Variable \(v_i\) is observably stable when \(TrapSet(\{ x \in \mathbb{B}^n \mid x_i = true \}) \not= \emptyset\) or \(TrapSet(\{ x \in \mathbb{B}^n \mid x_i = false \}) \not= \emptyset\).

\(TrapSet\): Largest subset that cannot be escaped.

Skeleton network with logical intervention parameters \(p_i\):

\Gamma_i'(x) = (p_i \Rightarrow x_i) \land (\overline{p_i} \Rightarrow \Gamma_i(x))

Feasible interventions: Projection of \(TrapSet\) results to intervention parameters. 

Dataset and runtime

https://github.com/sybila/biodivine-boolean-models

145 real-world Boolean networks from various sources:

  • 15 contain non-monotonic interactions (i.e. ~10%).
  • Observably stable variables analysed for all networks.
  • Stabilising interventions timeout on 21 networks.

Results

  • 93/130 networks have at least one observably stable variable.
  • 26/130 networks have all variables observably stable.
  • These variables are typically found outside of negative feedback cycles.
  • 31/83 networks require intervention of size one or two.
  • 6/83 networks require intervention of 10 or more.
  • Interventions often align with feedback vertex set of IG, but can be smaller.

Discussion

  • Skeleton network provides a "computational" alternative to existing "analytical" methods.
  • When applied to full influence graphs, the results are largely comparable to other static analysis methods.

Future Work

  • The skeleton construction can be also applied per update function---approximating partially known but incomplete networks.

Variable Stabilisation in Boolean Monotonic Pools

By Samuel Pastva

Made with Slides.com

Variable Stabilisation in Boolean Monotonic Pools

  • 55

More from Samuel Pastva