Bifurcation analysis of logical models in systems biology

Sam Pastva

Modelling gene interactions

Gene X @DNA

Gene X @mRNA

Protein X

Gene Y @DNA

Gene Y @mRNA

Protein Y

\(\oplus\)

\(\ominus\)

Gene X

Gene Y

Gene Regulatory Network (GRN)

Gene X

Gene A

Gene B

Gene C

Do we need both A and C, or just one? Does B interact with A and C equally or not?

f_{A}(x) = \neg x_{C}

x \in \{0,1\}^n~\text{(state)}

f_{B}(x) = x_{A}

f_{C}(x) = x_{C} \lor (x_{A} \land \neg x_{B})

Boolean Network (BN)

f_{A}(x) = \neg x_{C}

f_{B}(x) = x_{A}

f_{C}(x) = x_{C} \lor (x_{A} \land \neg x_{B})

000

100

111

011

001

Synchronous update: all updates happen at the same time.

000

100

110

101

001

111

011

Asynchronous update: better captures unknown process time-scales.

What "outcomes" are possible in our model? (Attractors - bottom SCCs)

Single state (fixed-point attractor)
Larger region (complex attractor)
- cycle (oscillation)
- other (disorder)

110

Assumption: chemistry is fair. Only terminal states/components can be attractors.

Different attractors can represent different biological functionality (phenotype).

Addressing model uncertainty

Logical parameters (network inputs)

Functional parameters: (partially) unknown dynamics

Gene X

Gene Y

Input A

f_{C}(x) = x_{C} \lor {\color{red} F(x_{A}, x_{B})}

Exponentially many "outcomes" for logical parameters, double exponential for functional parameters.

Benes, N., Brim, L., Pastva, S., Polácek, J., & Šafránek, D. (2019). Formal Analysis of Qualitative Long-Term Behaviour in Parametrised Boolean Networks. ICFEM.

Depending on system's parameters, which outcomes are "similar" and which are "different"?

Bifurcation analysis:

Bifurcation theory of continuous dynamical systems

Cont. dynamical system: (simplified)

A set of deterministic trajectories in \(\mathbb{R}^n\)

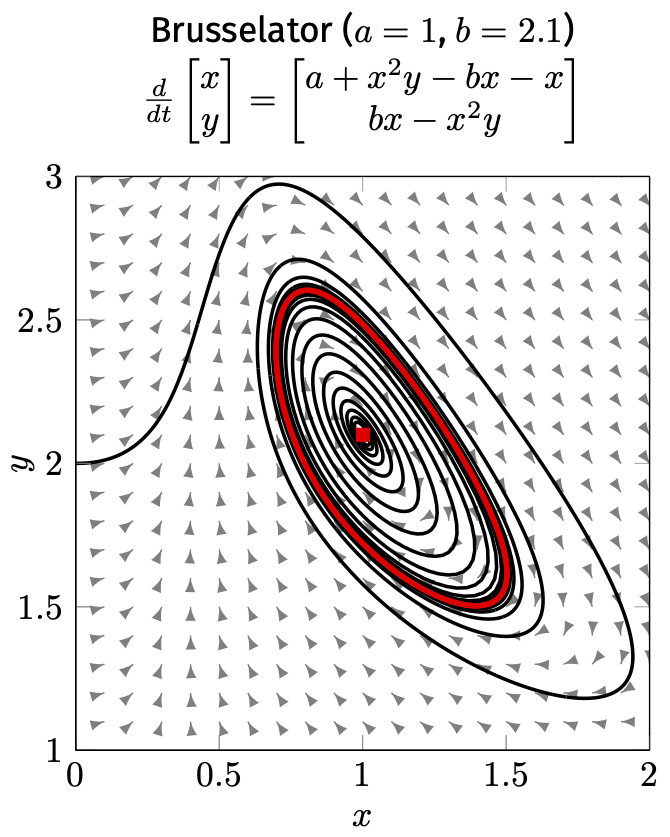
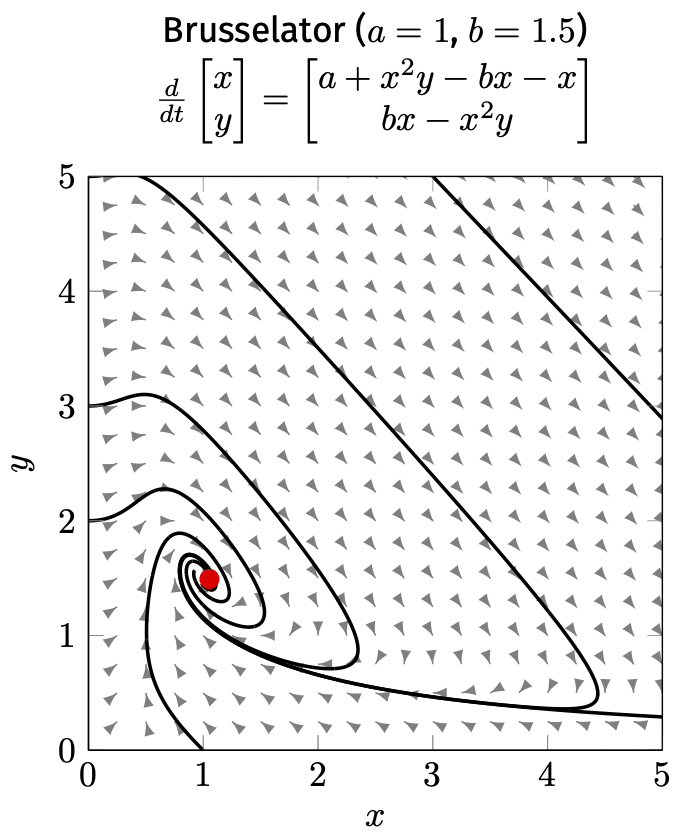
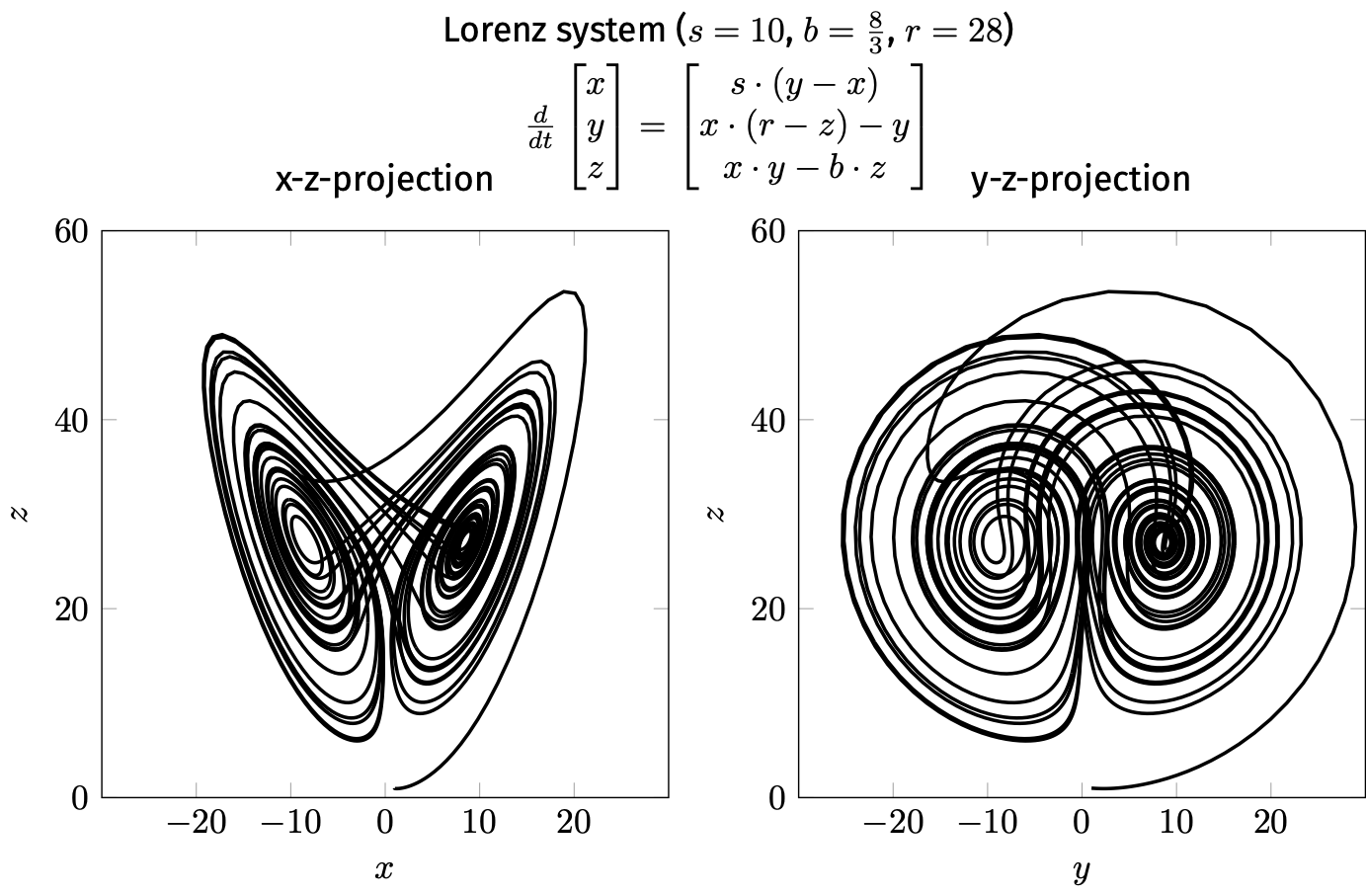
"Similar" vs. "different":

Topological equivalence (continuous transformation of trajectories)

Topological equivalence recognises similar patterns (e.g. attractors, repellers) that we saw in the discrete world:

fixed-point

cycle

chaos

Bifurcation diagram: A (visual) partitioning of the parameter space into topologically equivalent classes.

There is clearly an intuitive link between what we consider "similar long-term behaviour" in continuous and logical models.

Can we take inspiration from the "classical" bifurcation theory to enrich analysis of logical models?

Is there a possible counterpart to the topological equivalence?

How do we compute the parameter space decomposition?

What about "logical" bifurcation diagrams?

Equivalence of behaviours

* Shahrad Jamshidi, Heike Siebert, and Alexander Bockmayr. “Preservation of dynamic properties in qualitative modeling frameworks for gene regulatory networks”. In: Biosystems 112.2 (2013)

Topological equivalence on transition systems is an isomorphism (not interesting).
Classical bifurcation theory has no concept of non-determinism or fairness.
Logical and continuous models of the same system often have fundamental differences in behaviour.*

(all models are wrong, some models are useful)

Alternative equivalence

Take all valid runs of your system. (reflecting fairness, finiteness, time domain, initial states, etc.)

Alternative equivalence

Take all valid runs of your system.
Pick the smallest set of states that partitions these runs into finite segments.

Alternative equivalence

Take all valid runs of your system.
Pick the smallest set of states that partitions these runs into finite segments.
Make a new graph from these states, based on the reachability in the original system.

Alternative equivalence

Take all valid runs of your system.
Pick the smallest set of states that partitions these runs into finite segments.
Make a new graph from these states, based on the reachability in the original system.
Two systems are equivalent if these condensed graphs are isomorphic.

\(\sim\)

In a fair system (e.g. BN), one representative state per attractor (bottom SCC) and repeller (top SCC) is selected. As fairness "decreases", more SCCs need to be included.

In a fair system, one representative state per SCC is sufficient. As fairness "decreases", more states need to be selected, up to the number of independent cycles.

Back to basics: (Bottom) SCC detection for asynchronous Boolean networks

Binary Decision Diagrams

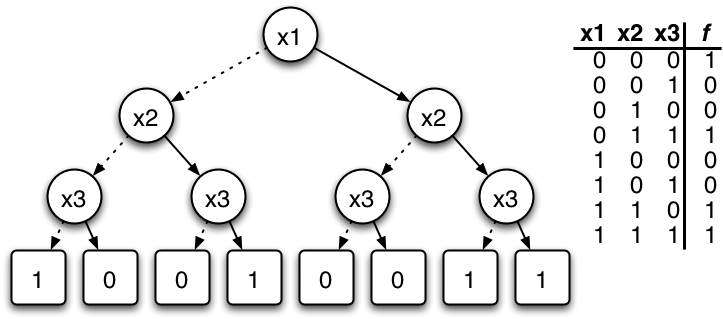
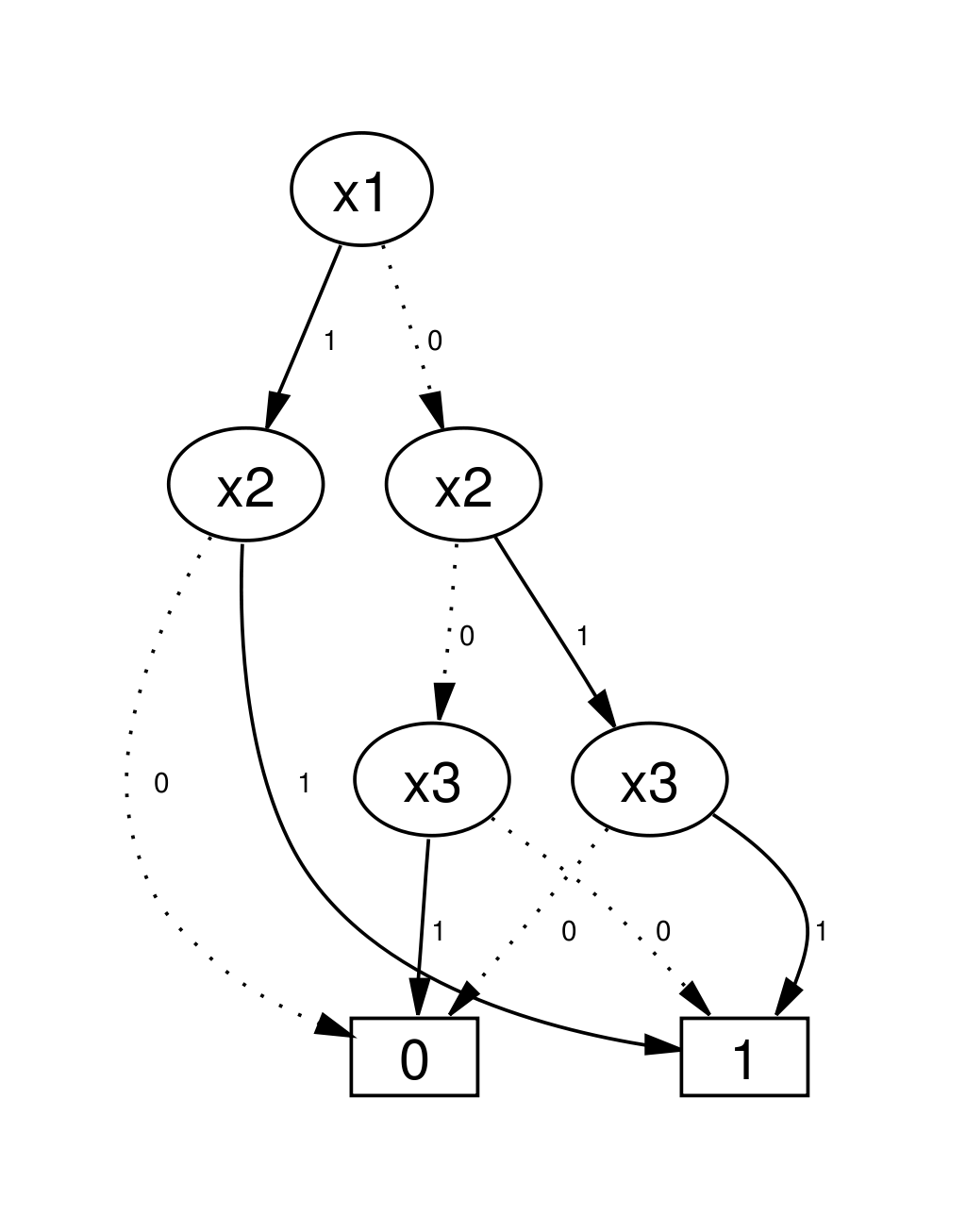
Parametrisation+State of a BN is a bit-vector. Sets/relations of these can be encoded via Boolean functions.

s \in X \Leftrightarrow f_{BDD(X)}(s) = 1~(\text{with}~X \subseteq \{0,1\}^{k})

Set operations correspond to logical operations on functions (and graph operations on BDDs)

X \cap Y \equiv f_{BDD(X)} \land f_{BDD(Y)}

Since Boolean network is described by Boolean functions, computing successors/predecessors (including parameters) is relatively straightforward.

Benes, N., Brim, L., Pastva, S., & Šafránek, D. (2022). BDD-Based Algorithm for SCC Decomposition of Edge-Coloured Graphs. Log. Methods Comput. Sci., 18.

\mathcal{O}(n^2)~\text{symbolic operations}

\mathcal{O}(n)~\text{symbolic operations}

\mathcal{O}(n)

\mathcal{O}(n^3)

The first case is in pracitce much better!

Nobody can usually give you such guarantees...

Benes, N., Brim, L., Pastva, S., & Šafránek, D. (2021). Computing Bottom SCCs Symbolically Using Transition Guided Reduction. CAV.

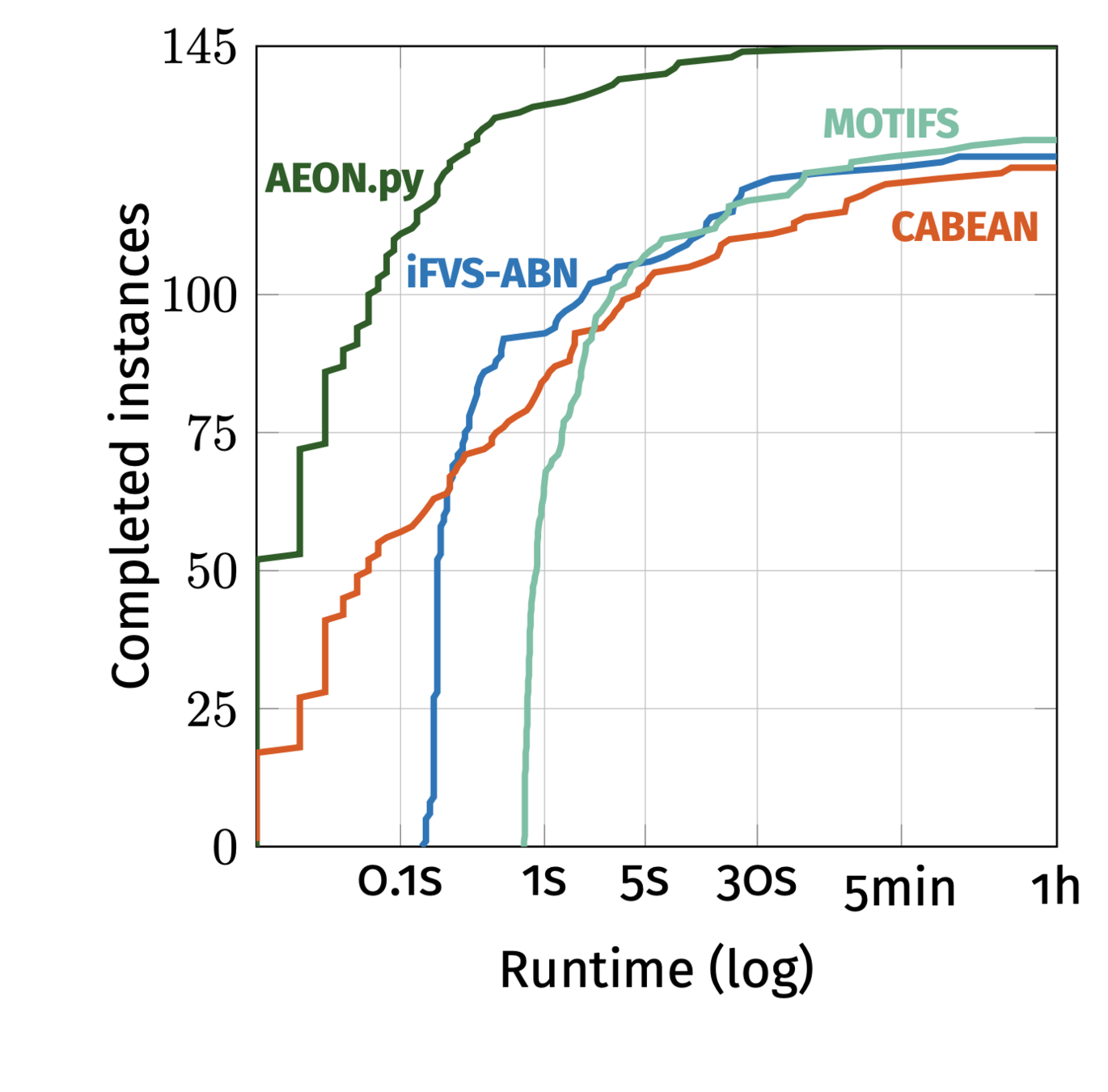
BDDs generally don't work, except when they do.

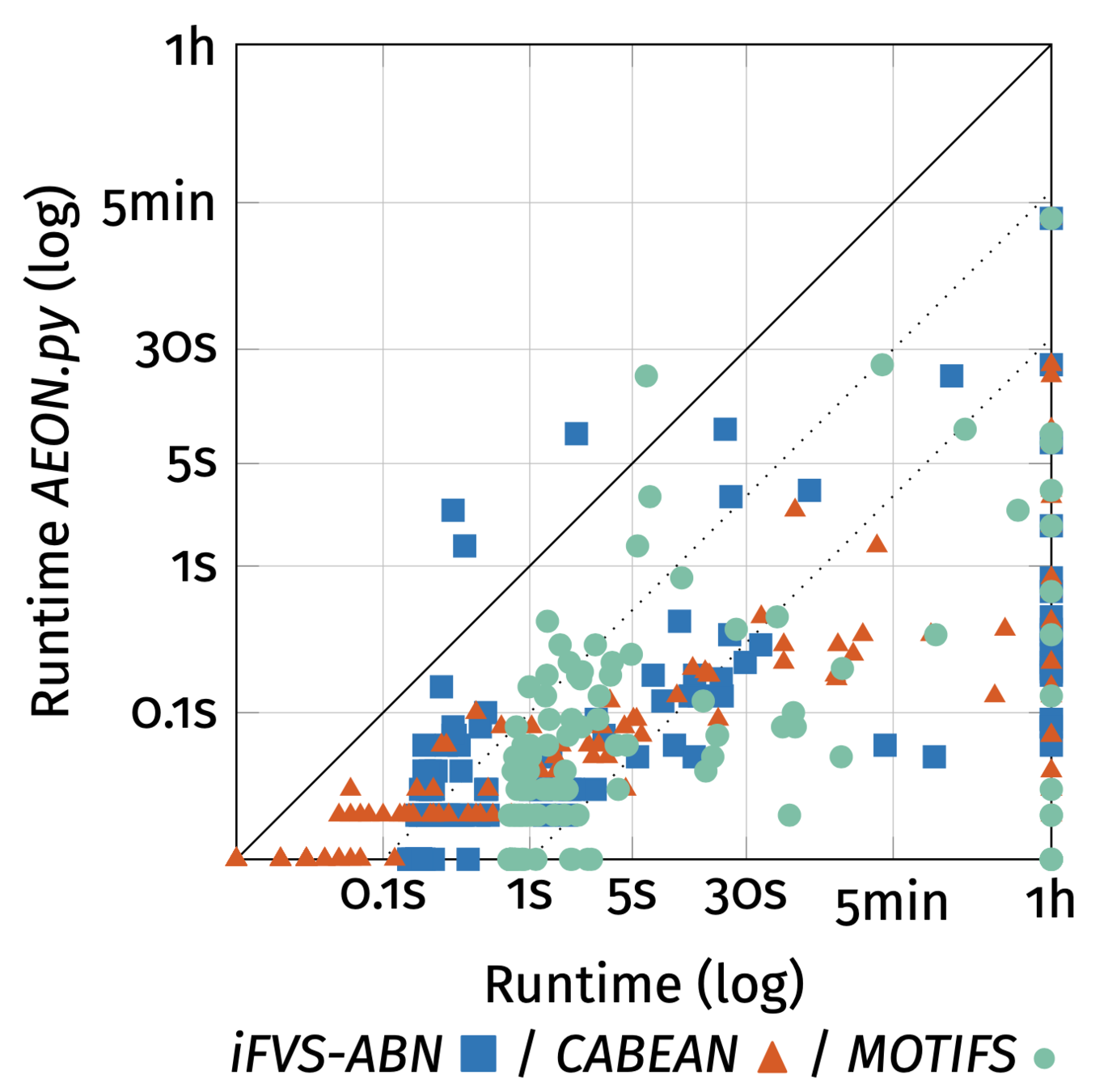
We have a parameter space partitioning.
We know how to compute it. (e.g. for 50+ Boolean parameters)
How can we show it to you?

Bifurcation decision tree

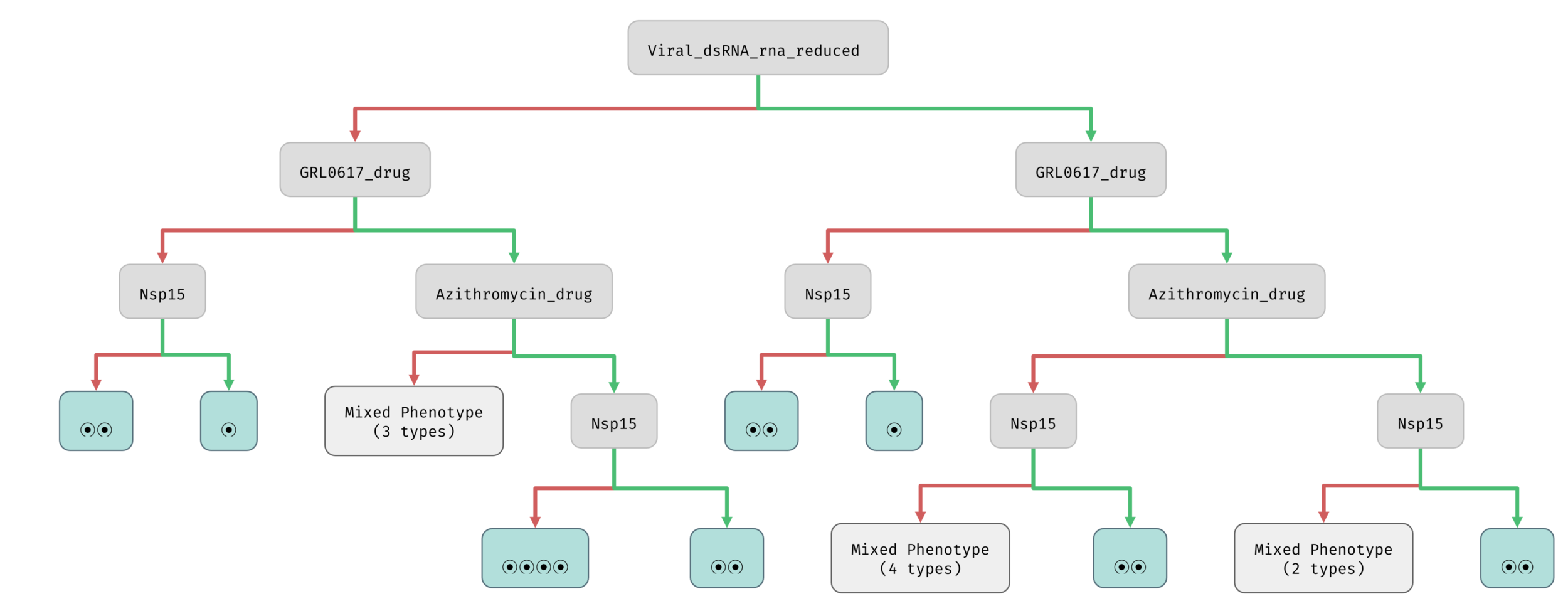
Different outcomes (classes of attractors)

Network parameters

Interactive, on-the-fly construction

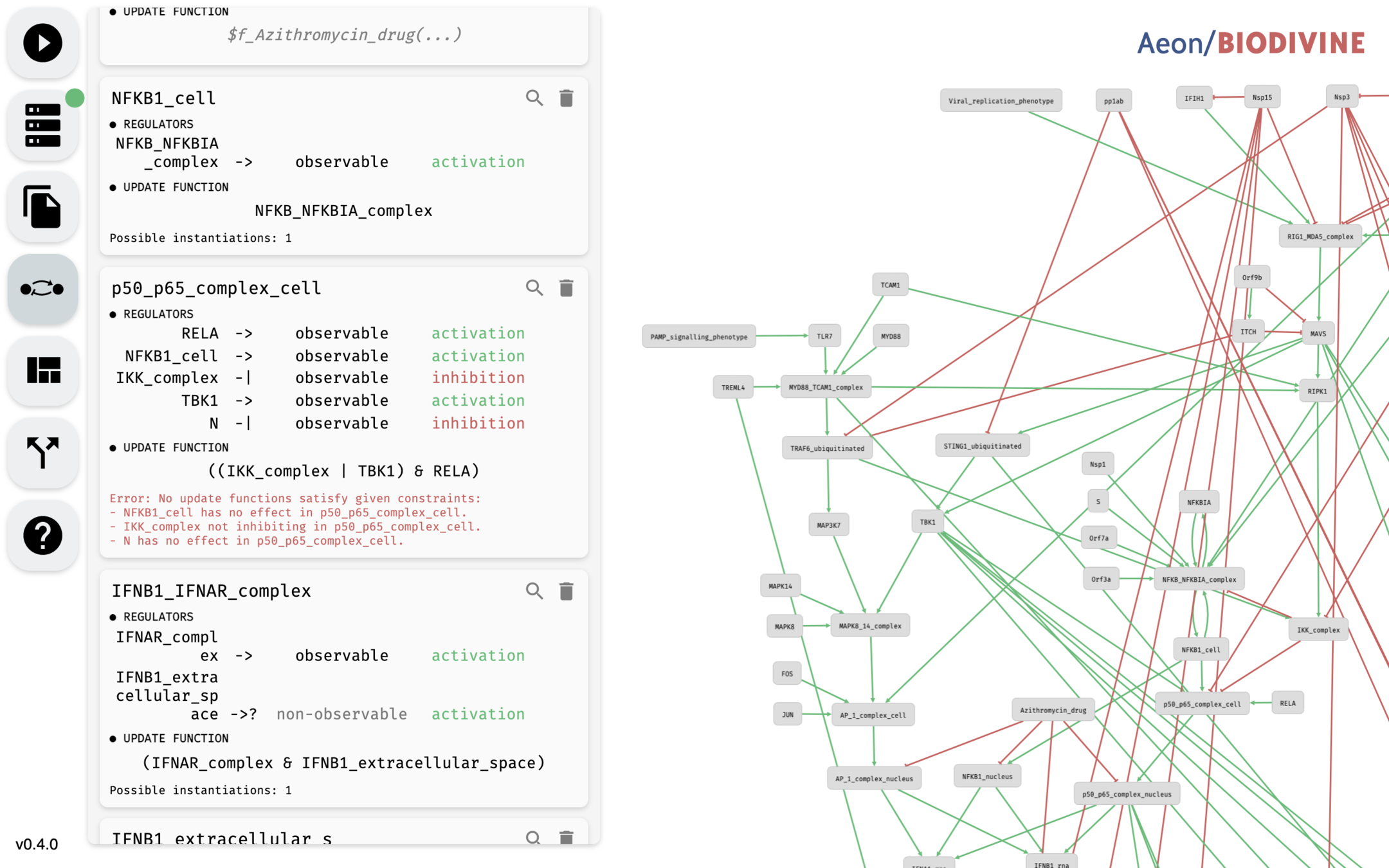
AEON

Interactive web-based network and decision tree editor.
Rust backend running symbolic BDD algorithms.
Python API wrapper for use in Jupyter notebooks.

Benes, N., Brim, L., Kadlecaj, J., Pastva, S., & Šafránek, D. (2020). AEON: Attractor Bifurcation Analysis of Parametrised Boolean Networks. CAV.

Benes, N., Brim, L., Huvar, O., Pastva, S., Šafránek, D., & Smijáková, E. (2022). AEON.py: Python Library for Attractor Analysis in Asynchronous Boolean Networks. Bioinformatics.

T-cell survival network

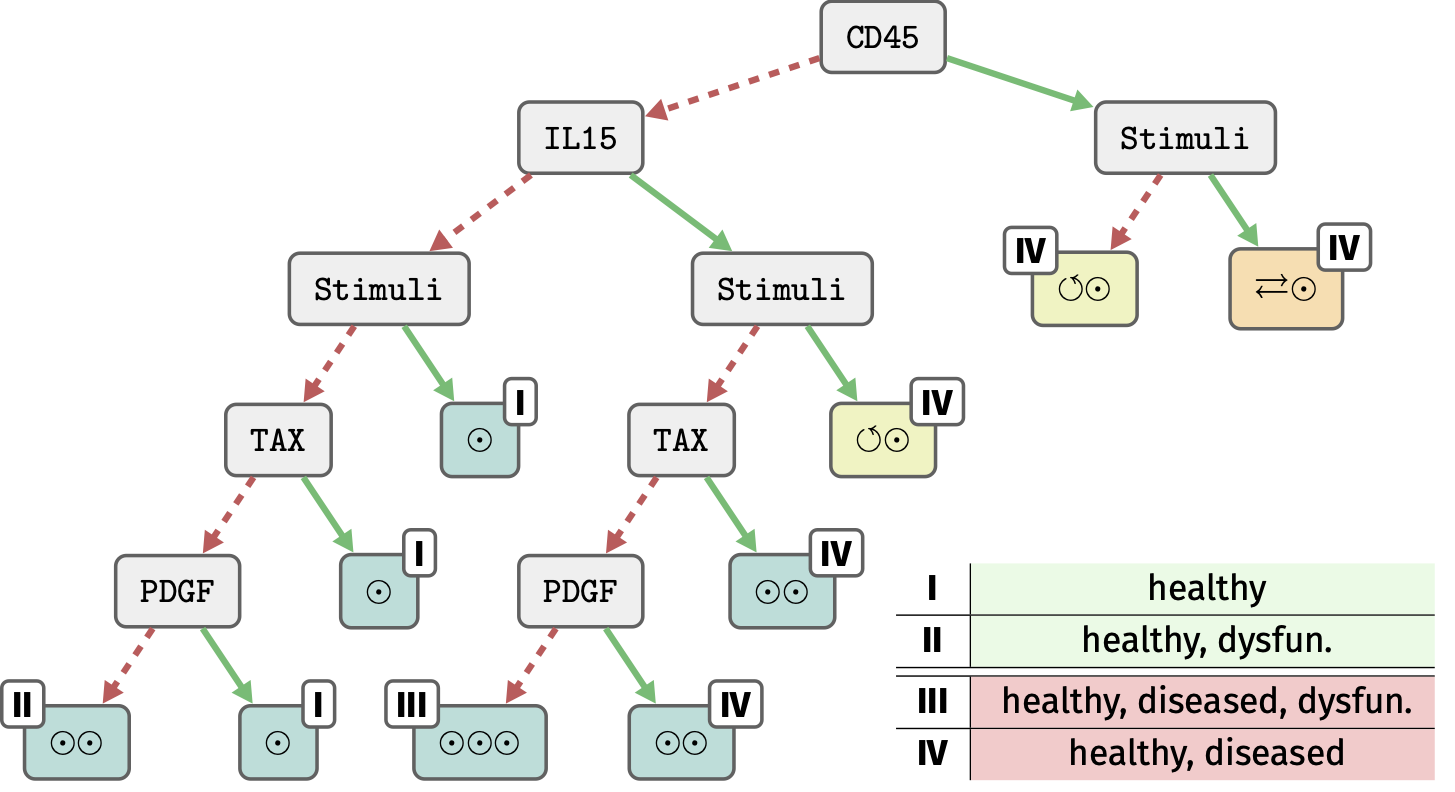
Zhang, R., et al. (2008). Network model of survival signaling in large granular lymphocyte leukemia. Proceedings of the National Academy of Sciences, 105, 16308 - 16313.

Newly characterised "phenotype"

Butanol pathway repair

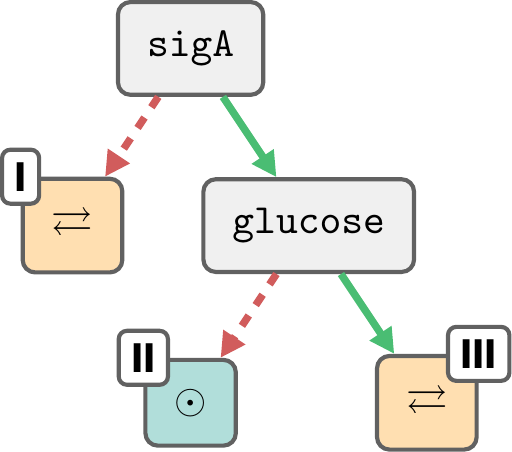
Out of 13 parameters, only 2 play a role in the long-term behaviour.

This relationship is maintained regardless of \(F_1, F_2, F_3\).

But we can further narrow down \(F_1, F_2, F_3\) through other means...

Jana Musilová. “Signaling pathway for butanol produc- tion in solventogenic clostridium bacteria”. MA thesis. Brno University of Technology, 2019.

Summary

Computer science can stydy gene regulation through the lens of Boolean networks.
Logical and functional parameters play a critical role in the long-term behaviour of Boolean networks.
Symbolic methods can often work quite well as long as you are aware of the tradeoffs.
Useful results are explainable: embrace interactivity and flexibility in communication.

For details, meet me in room 01.02.073 :)