


Computational Biology
(BIOSC 1540)
Feb 13, 2025
Lecture 06B
Read mapping
Methodology
Announcements
Assignments
Quizzes
CBytes
ATP until the next reward: 653
After today, you should have a better understanding of
The purpose of reference-based mapping
Understanding how we get our reads
Cells will transcribe these genes into mRNA (i.e., transcripts)
We collect, convert to complementary DNA, and then amplify
Suppose we have the following three coding (i.e., genes) and non-coding regions with introns and exons
DNA
Understanding how we get our reads
Fragmentation and sequencing
FASTQ reads
Each RNA-seq read represents a small fragment of a transcript
Our purified sample
The Goal of Read Alignment is to Reconstruct Gene Expression Patterns
By mapping reads to a reference genome or transcriptome, we can:
- Identify which genes are active in a sample.
- Measure the relative abundance of different transcripts.
- Detect novel isoforms and alternative splicing events.
DNA
Reads
Read mapping determines where in the genome did these reads originate from.
RNA-seq must account for alternative splicing
DNA
Reads
Unlike DNA sequencing, RNA sequencing includes spliced transcripts.
Key problem: Reads from mRNA span exon-exon junctions, but the genome contains introns.
Solution: Transcriptomic aligners must allow for gapped alignments that bridge exon-exon junctions.
After today, you should have a better understanding of
Hash-based methods for handling introns
Activity
Read mapping exercise
The reads below were built by taking random words, slicing three letters, and then concatenating without spaces (all lowercase)
In groups, please work together to determine which words were used for your read
Be prepared to explain how you approached the problem
Danny loved spotting shapes in the clouds and had an entire journal filled with sketches of dragons, castles, and sailing ships. One day, he noticed a small cloud following him, shifting to match whatever he imagined. He tested it by thinking of a giant ice cream cone; sure enough, it transformed before his eyes. Delighted, he ran home, wondering how much fun he could have with a personal cloud. His only concern was making sure it didn’t rain inside his room.
Let's consider this short story as our genome containing coding and non-coding regions
0. danclodrashi
"Danny clouds dragons ships"
1. entmagcretra
2. spomatwoncon
3. notgiasaibed
4. lovdrathirai
?
?
?
?
We could do maybe one or two in a few minutes
What about doing 30?
We need to map millions of reads to our genome, so how could we approach this computationally?
danclodrashi
lovshaentjou
spofilskecas
saionenotsma
clofolshimat
whaimatestthi
giaicecrecon
surenotratrig
befeyedelran
homwonmucfun
cloonlconmak
surdidraiins
danlovsposke
shajoufildra
cassaishiday
notclofolshi
matwhaimates
thigiaicecre
consurenotra
couhavwitper
rigbefeyedel
ranhomwonmuc
funcouhavwit
percloonlcon
maksurdidrai
insbeddanlov
sposhacloent
joufilskedra
casnotsmaclo
folshimathwa

After today, you should have a better understanding of
Hash-based methods for handling introns
K-mer indexing
We can pre-compute k-mer locations of our story
Danny loved spotting shapes in the clouds and had an entire journal filled with sketches of dragons, castles, and sailing ships [...]
We can chunk our story into k-mers and store where in the story they occur
"dan": [0]
"ann": [1]
"nny": [2]"clo": [35, 153, 382]
"lou": [36, 154, 383]
"oud": [37, 155, 384]
danny
clouds, cloud, cloud
"ing": [17, 116, 165, 178, 233, 335, 412]spotting, sailing, following, shifting, thinking, wondering, making
We can store these k-mers and indices and then use these to find potential sources
Mapping a read to our genome involves checking where k-mers exist
danclodrashi
Danny loved spotting shapes in the clouds and had an entire journal filled with sketches of dragons, castles, and sailing ships [...]
dan, clo, dra, shi
Read
Genome
Query k-mers
Check if k-mers are in our genome and the starting index of that k-mer
"dan": [0]
"clo": [35, 153, 382]
"dra": [92]
"shi": [120, 173]clouds, cloud, cloud
danny
dragon
ships, shifting
This data structure is called a hash table (i.e., dictionary in Python)
Hash tables link a key to a value
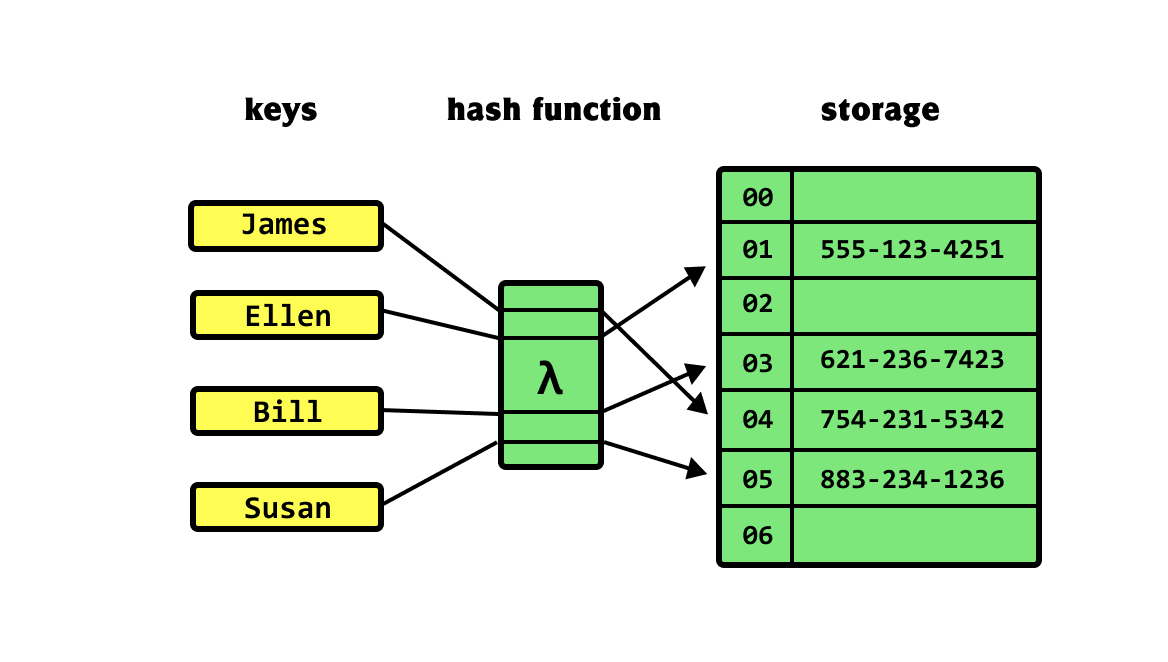
Keys represent a "label" we can use to get information
Example: Phone book / Contacts list
Name
A "hash function" determines where to find their number in our computer's memory
Number
Hashing our reference genome seeds our hash table with k-mer locations
5-mers
TACGT, ACGTA, CGTAC, GTACG, . . .
Reference genome
0
10
TACGTACGATAGTCGACTAGCATGCATGCTACGTGCTAGCACGTATGCATGCATGCATGCC
20
30
40
50
60
We hash our k-mer, and add the starting index where that k-mer occurs in our reference genome
TACGT
[1, 40]
h(k)
ACGTA
[0, 29]
k-mer location in genome
k-mer
Hashing our RNA-seq data provides quick lookups of our reference genome
Query a k-mer read to get indices that of possible reference genome locations
Reference genome
Hash table
TACGT
[0, 29]
ACGTA
[1, 40]
k-mer location in genome
k-mer
h(k)
0
10
TACGTACGATAGTCGACTAGCATGCATGCTACGTGCTAGCACGTATGCATGCATGCA
20
30
40
50
After today, you should have a better understanding of
Suffix arrays for efficient substring searches
Hash-Based Alignment: Divide and Conquer
A "DNA dictionary" with quick lookup and direct access to potential matches
Pros
- Easily parallelizable
- Flexible for allowing mismatches
- Conceptually simple
Cons
- Large memory footprint for index
- Can be slower for very large genomes
"dan": [0]
"clo": [35, 153, 382]
"dra": [92]
"shi": [120, 173]Suffix trees compress all k-mers into a single data structure
NA
NA$
$
4
2
0
1
3
5
A
$
NA
$
NA$
Root node
(Start here)
BANANA
$
A suffix tree is used to find starting index of suffix
Nowhere.
Edge
Node
Leaf node
Split point
Suffix start index
Next part of suffix
Where does start?
AANA
Index 2.
Example: Where does
start?
NANA$
Note: We use $ to represent the end of a string
Suffix arrays are memory-efficient alternatives to trees
BANANA
$
Requires less memory, but is also less powerful
1. Create all suffixes
2. Sort lexicographically
BANANA
$
ANANA
$
NANA
$
NA
$
ANA
$
A
$
$
3. Store starting indices in original string
6
5
3
1
0
4
2
$ comes before letters for sorting
String index
BANANA
$
ANANA
$
NANA
$
NA
$
ANA
$
A
$
$
Suffix
After today, you should have a better understanding of
Burrows-Wheeler Transform (BWT) string compression
Compression reduces the amount of data we have to store
"Alex keeps talking and talking and talking and talking and eventually stops."
Suppose we need to store this string:
How could we store this string and save space?

"talking and talking and talking and talking and"
"talking and" 4
=
"Alex keeps talking and talking and talking and talking and eventually stops."
"Alex keeps" + "talking and" 4 +"eventually stops."
Run-length encoding
Not all strings have repeats
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Donec iaculis risus vulputate dui condimentum congue. Pellentesque habitant morbi tristique senectus et netus et malesuada fames ac turpis egestas.
Can you find any repeats?

How can we force repeats?
Sorting the letters does!
.aaaaaaaaaaaabbcccccccccddddddeeeeeeeeeeeeeeeeeeeeeeefggghiiiiiiiiiiiiiiiillllllllmmmmmmmmnnnnnnnnnnoooooooopppppqqrrrrrrrssssssssssssssssstttttttttttttttttttuuuuuuuuuuuuuuuv
a12b2c9d6e23f1g3h1i16l8m8n10o8p5q2r7s17t19u15v1
Run-length encoding
Sorting lexicographically forces repeats, but loses original data
The Burrows-Wheeler Transform (BWT) is a way to sort our strings without losing the original data
(And also search through it!)
Developed by Michael Burrows and David Wheeler in 1994
Basic concept of BWT
- Append a unique end-of-string (EOS) marker to the input string.
- Generate all rotations of the string.
- Sort these rotations lexicographically.
- Extract the last column of the sorted matrix as the BWT output.
BANANA
$
A
$
BANAN
NA
$
BANA
$
BANANA
ANA
$
BAN
NANA
$
BA
ANANA
$
B
BANANA
$
A
$
BANAN
NA
$
BANA
$
BANANA
ANA
$
BAN
NANA
$
BA
ANANA
$
B
ANNB$AA
BANANA
First column is more compressible, but we lose context and reversibility
(We can also get first column by sorting the output)
After today, you should have a better understanding of
FM-index for efficient substring searches
Enhancing BWT for Rapid Searching
ABRACADABRA$
ABRACADABR
$ABRACADAB
BRA$ABRACA
BRACADABRA
CADABRA$AB
DABRA$ABRA
RA$ABRACAD
RACADABRA$
ADABRA$ABR
ABRA$ABRAC
A$ABRACADA
ACADABRA$A
$
A0
A1
A2
A3
A4
B0
B1
C0
D0
R1
R0
A0
R0
D0
$
R1
C0
A1
A2
A3
A4
B1
B0
ABRACADABR
$ABRACADAB
BRA$ABRACA
BRACADABRA
CADABRA$AB
DABRA$ABRA
RA$ABRACAD
RACADABRA$
ADABRA$ABR
ABRA$ABRAC
A$ABRACADA
ACADABRA$A
$
A
A
A
A
A
B
B
C
D
R
R
A
R
D
$
R
C
A
A
A
A
B
B
The backward search algorithm efficiently finds occurrences of a pattern in a text using the LF-mapping
BWT matrix
Number
Number characters with the number of times they have appeard
F-column
L-column
We are dealing with enormous datasets
Reference genome sizes
- Homo sapiens: 3,200,000,000 bp
- Mus musculus: 2,700,000,000 bp
- Drosophila melanogaster: 140,000,000 bp
- Saccharomyces cerevisiae: 12,000,000 bp
(~3.2 GB if using u8)
RNA-seq data
Contextualization
The best movie ever is only 1.2 GB
Most computers have 8 - 12 GB of RAM

ABRACADABRA$
ABRA
Suppose I want to find where
is located
1. Find rows with last character in search string (e.g., A) in F-column
2. Note which rows has the next letter (e.g., R) in L-column
3. Work backwards in search string until the first letter
A0
R0
D0
$
R1
C0
A1
A2
A3
A4
B1
B0
$
A0
A1
A2
A3
A4
B0
B1
C0
D0
R1
R0
A
R
ABRACADABR
$ABRACADAB
BRA$ABRACA
BRACADABRA
CADABRA$AB
DABRA$ABRA
RA$ABRACAD
RACADABRA$
ADABRA$ABR
ABRA$ABRAC
A$ABRACADA
ACADABRA$A
A0
R0
D0
$
R1
C0
A1
A2
A3
A4
B1
B0
$
A0
A1
A2
A3
A4
B0
B1
C0
D0
R1
R0
R
B
ABRACADABR
$ABRACADAB
BRA$ABRACA
BRACADABRA
CADABRA$AB
DABRA$ABRA
RA$ABRACAD
RACADABRA$
ADABRA$ABR
ABRA$ABRAC
A$ABRACADA
ACADABRA$A
A0
R0
D0
$
R1
C0
A1
A2
A3
A4
B1
B0
$
A0
A1
A2
A3
A4
B0
B1
C0
D0
R1
R0
B
A
ABRACADABR
$ABRACADAB
BRA$ABRACA
BRACADABRA
CADABRA$AB
DABRA$ABRA
RA$ABRACAD
RACADABRA$
ADABRA$ABR
ABRA$ABRAC
A$ABRACADA
ACADABRA$A
Backward search enables efficient searching using only first and last columns of BWT
BWT practice
Given the string "mississippi$", complete the following tasks:
- Construct the Burrows-Wheeler Transform (BWT) of the string.
- Use the LF-mapping to find the number and positions of occurrences of the following patterns in the original string:
- a) "si"
- b) "iss"
- c) "pp"
After today, you should have a better understanding of
Splice-aware mapping with seed-chain-extend strategy
Seed-and-extend in hash-based alignment
Seed
Extend
Read: ATCGATTGCA
k-mers (k=3)
ATC, TCG, CGA, GAT, ATT, TTG, TGC, GCA
Use hash table for rapid lookup of potential matches quickly
Start from seed match and grow in both directions with reference genome
CCGTATCGATTGCAGATG
GAT
[7, 14]
h(k)
Check to see if we can align the read to reference
Before the next class, you should
Lecture 07A:
Quantification -
Foundations
Lecture 06B:
Sequence alignment -
Methodology
Today
Tuesday
Quiz 02
N
A
N
B
$
A
A
A
A
A
$
B
N
N
A
A
A
$
B
N
N
N
A
N
B
$
A
A
AN
AN
A$
$B
BA
NA
NA
AN
AN
A$
$B
BA
NA
NA
N
A
N
B
$
A
A
ANA
ANA
A$B
$BA
BAN
NAN
NA$
ANA
ANA
A$B
$BA
BAN
NAN
NA$
N
A
N
B
$
A
A
BWT output is reversible!
ANAN
ANA$
A$BA
$BAN
BANA
NANA
NA$B
BANANA$
NANA$BA
NA$BANA
A$BANAN
$BANANA
ANANA$B
ANA$BAN
- Write BWT output "vertically"
- Sort each row starting from the left-most character
- Append the same BWT output
- Repeat until finished (length of rows equal BWT output length)
2
3
2
3
2
3
2
...
Hash functions convert labels to table indices

Index: We take the key, count how many characters are in it
Note: This is a bad hashing function since "Alex" and "John" would result in the same index
Example
len("James") = 5
James
883-234-1236
BIOSC 1540: L06B (Read mapping)
By aalexmmaldonado
BIOSC 1540: L06B (Read mapping)
- 253



