
Занятие №11:
Задачи физики сводящиеся к системам диф. уравнений

Второй закон Ньютона

Постановка задачи
\vec{F}_p
=
Некоторая среда, оказывающая сопротивление движению
Двигающееся тело
Сила, "разгоняющая" тело
Сила, како-го нибудь внешнего поля (гравитации, электричества, ...)
\vec{F}_{\text{тяжести}}
+
\vec{F}_{\text{тяги}}
+
\vec{F}_{\text{сопротивления}}
\vec{F}_p
=
m\vec{a}
+
...
...

Ускорение
=
\vec{a}
\dfrac{d\vec{v}}{dt}
=
\dfrac{d^2\vec{r}}{dt^2}
\vec{r} = \{x, y\}
\vec{a} = \{a_x, a_y\}
\begin{cases}
a_x = \dfrac{d^2x}{dt^2}\\
\\
a_y = \dfrac{d^2y}{dt^2}
\end{cases}
\vec{a}

Конечный вид
\begin{cases}
\dfrac{dx}{dt} = v_x\\
\\
\dfrac{dv_x}{dt} = a_x
\end{cases}
\dfrac{d^2x}{dt^2}:
\begin{cases}
\dfrac{dy}{dt} = v_y\\
\\
\dfrac{dv_y}{dt} = a_y
\end{cases}
\dfrac{d^2y}{dt^2}:
\cdot m
=
F_{px}
\cdot m
=
F_{py}
=
=
F_{1x}
+
F_{2x}
+
...
F_{1y}
+
F_{2y}
+
...

Пример - задача
Тело брошено под углом в 80 градусов к горизонту со скоростью 15 м/с. Определите закон изменения положения тела и смоделируйте его динамику.
\vec{F}_p
=
m\vec{g}
m\vec{a}
m\vec{g}
=
\vec{a}
\vec{g}
=
\{0, -g\}
\dfrac{dx}{dt} = v_x
\dfrac{dv_x}{dt}
\dfrac{dy}{dt} = v_y
\dfrac{dv_y}{dt} = -g
=
0
\vec{a}
=

Решение и анимация
import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
# Определяем переменную величину и количество кадров
frames = 200
t = np.linspace(0, 5, frames)
# Определяем функцию для системы диф. уравнений
def move_func(z, t):
x, v_x, y, v_y = z
dxdt = v_x
dv_xdt = 0
dydt = v_y
dv_ydt = - g
return dxdt, dv_xdt, dydt, dv_ydt# Определяем начальные значения и параметры
g = 9.8
v = 15
alpha = 80 * np.pi / 180
x0 = 0
v_x0 = v * np.cos(alpha)
y0 = 0
v_y0 = v * np.sin(alpha)
z0 = x0, v_x0, y0, v_y0
# Решаем систему диф. уравнений
def solve_func(i, key):
sol = odeint(move_func, z0, t)
if key == 'point':
x = sol[i, 0]
y = sol[i, 2]
else:
x = sol[:i, 0]
y = sol[:i, 2]
return x, y
# Строим решение в виде графика и анимируем
fig, ax = plt.subplots()
ball, = plt.plot([], [], 'o', color='r')
ball_line, = plt.plot([], [], '-', color='r')def animate(i):
ball.set_data(solve_func(i, 'point'))
ball_line.set_data(solve_func(i, 'line'))
ani = FuncAnimation(fig,
animate,
frames=frames,
interval=30)
edge = 15
ax.set_xlim(0, edge)
ax.set_ylim(0, edge)
plt.show()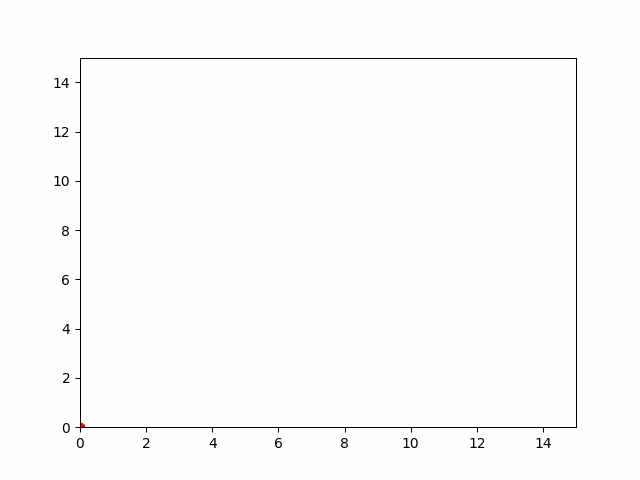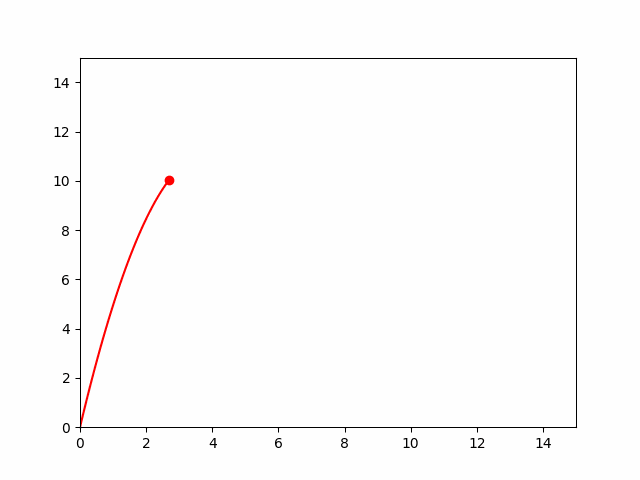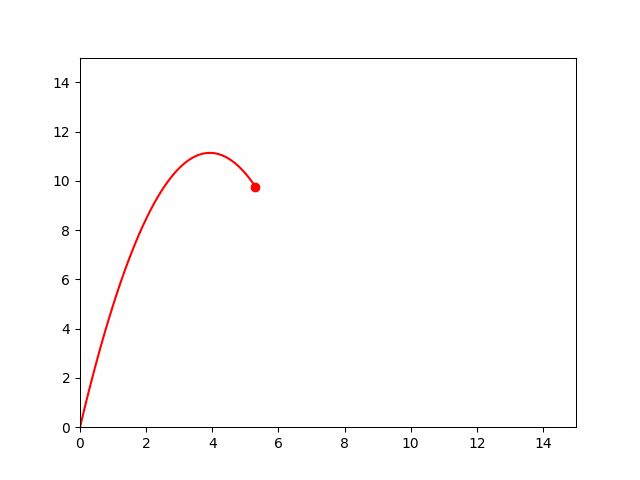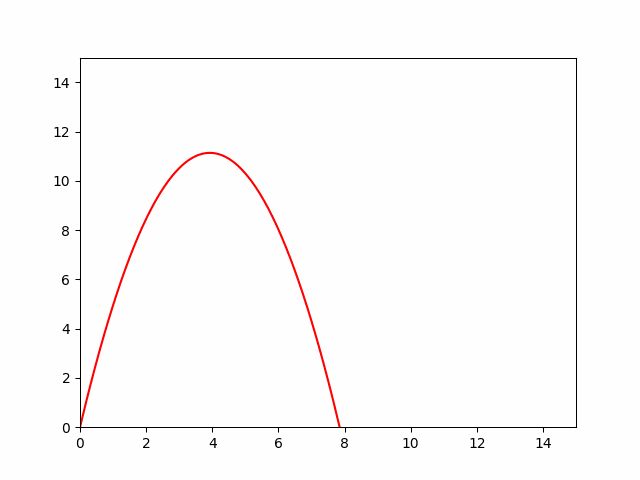

Спасибо за понимание!
Лекция №11. Задачи физики сводящиеся к системам диф. уравненийи
By Alexey Baigashov
Лекция №11. Задачи физики сводящиеся к системам диф. уравненийи
- 196



